Not all interventions are equal for the second peak

CAIMS-PIMS Coronavirus Modelling Conference

 

Joost Jorritsma,

joint with Tim Hulshof and Júlia Komjáthy

University of Technology Eindhoven

...is about...

  • Theoretical modeling of epidemics similar to COVID-19
  • Qualitative comparisons
  • Effect of:
    • network topology
    • space/geometry
    • interventions
    • temporary immunity

...is not about...

  • Predictions/data oriented modeling for COVID-19
  • Quantitative analysis

 

This talk...

Compartmental model

Two phases:

  • Subcritical: \(R_0=\beta/\gamma\le1\):
    epidemic vanishes
  • Supercritical: \(R_0>1\):
    exponential incline, long survival
  • Stationary solution

Susceptible

Infected

Temporary Immune

\(\beta I(t)/N\)

 \(\gamma\)

\(\eta\)

Mean-field model:

  • \(S(t), I(t), T(t)\in\mathbb{R}\)
  • well-mixed population

Susceptible

Infected

Infect neighbor w.p. \(\beta\)

 w.p. \(\gamma\)

w.p. \(\eta\)

Network approach

Temporary Immune

Compartmental vs. Network

Compartmental Network
Three parameters Underlying network
Analytic expression
Easier parameter fitting
Deterministic Stochastic
Well-mixed population Spatial component possible
Variability between nodes
Intuitive intervention modeling

Agree for complete graph

Choice of network

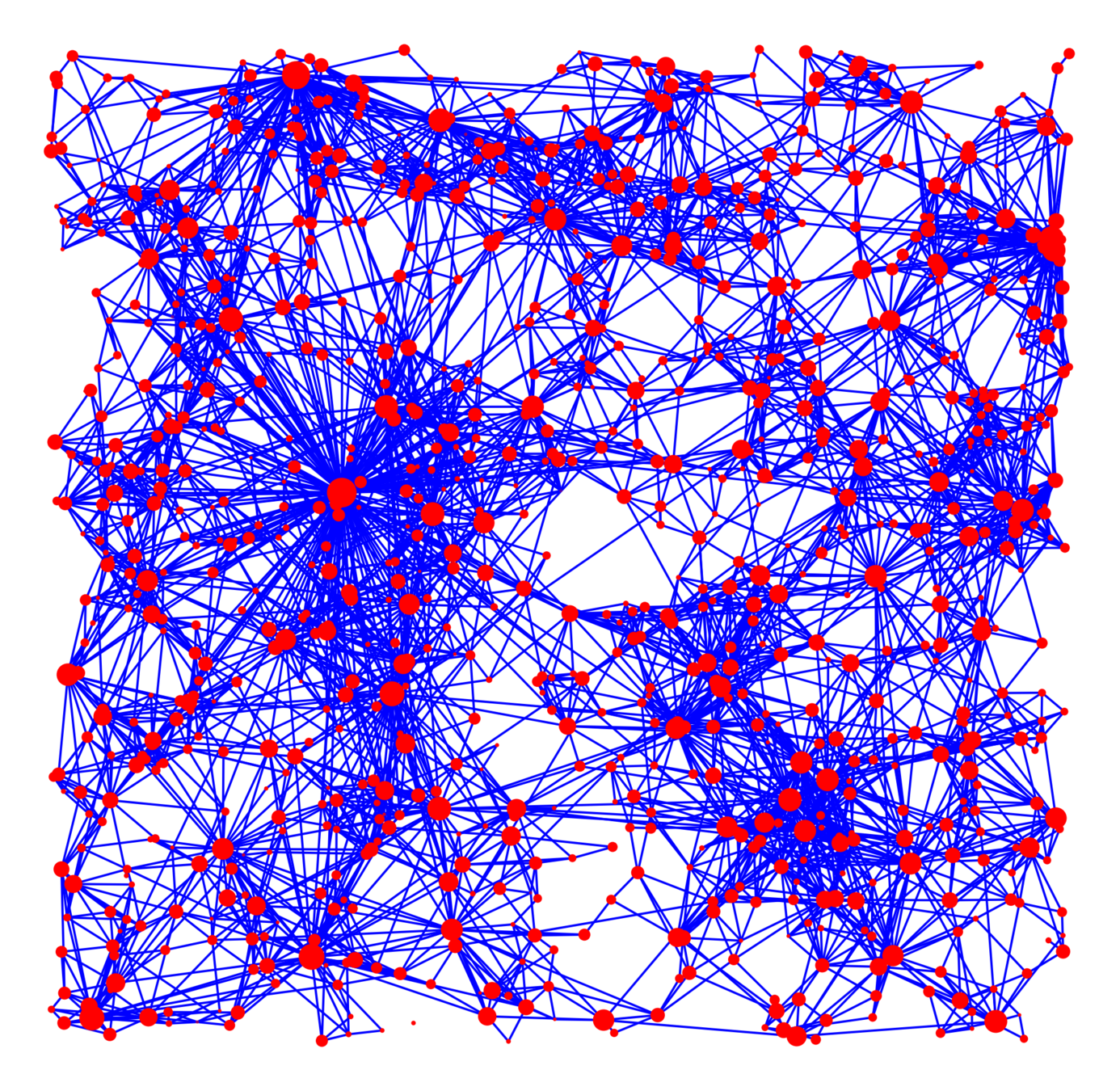
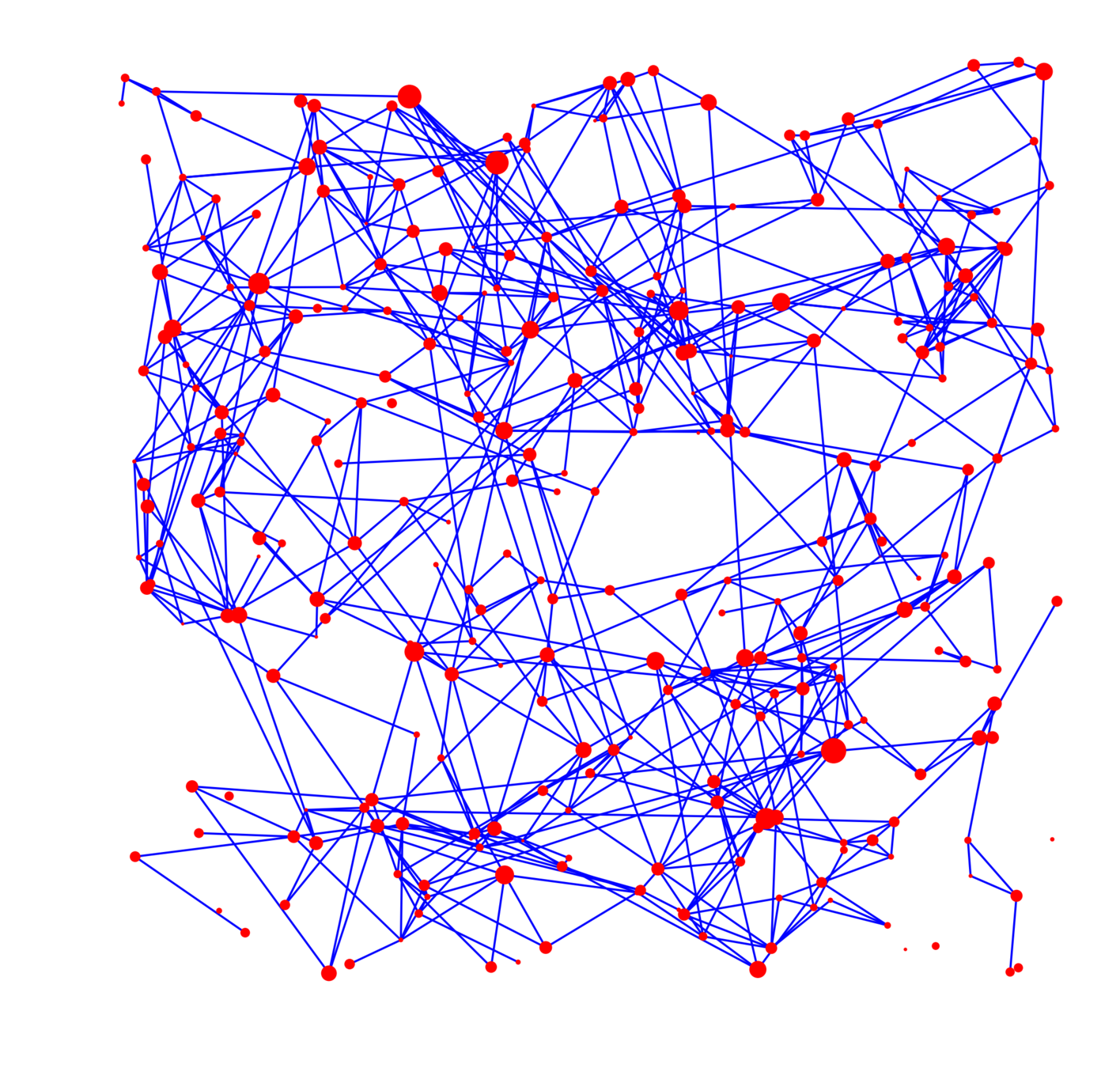
Geometric Inhomogeneous Random Graph

  • Spatially induced clustering,
    heavy-tailed degree distribution.
     
  • \(n\) nodes uniformly in \([0,\sqrt{n}]^{2}\).
  • Power-law weight/fitness for vertices:
     
     
  • Condition on weights & locations (\(\alpha>1\)):
\mathbb{P}(x\leftrightarrow y \mid W_x, W_y) \asymp \min\Big\{1, c \left(\frac{W_xW_y}{\|x-y\|^2}\right)^\alpha\Big\}.
\mathbb{P}(W\ge w) \asymp w^{-(\tau-1)}, \qquad \tau>2.
  • Smaller \(\tau\): more variability in weights/degrees.
  • Smaller \(\alpha\): more long-range connections.

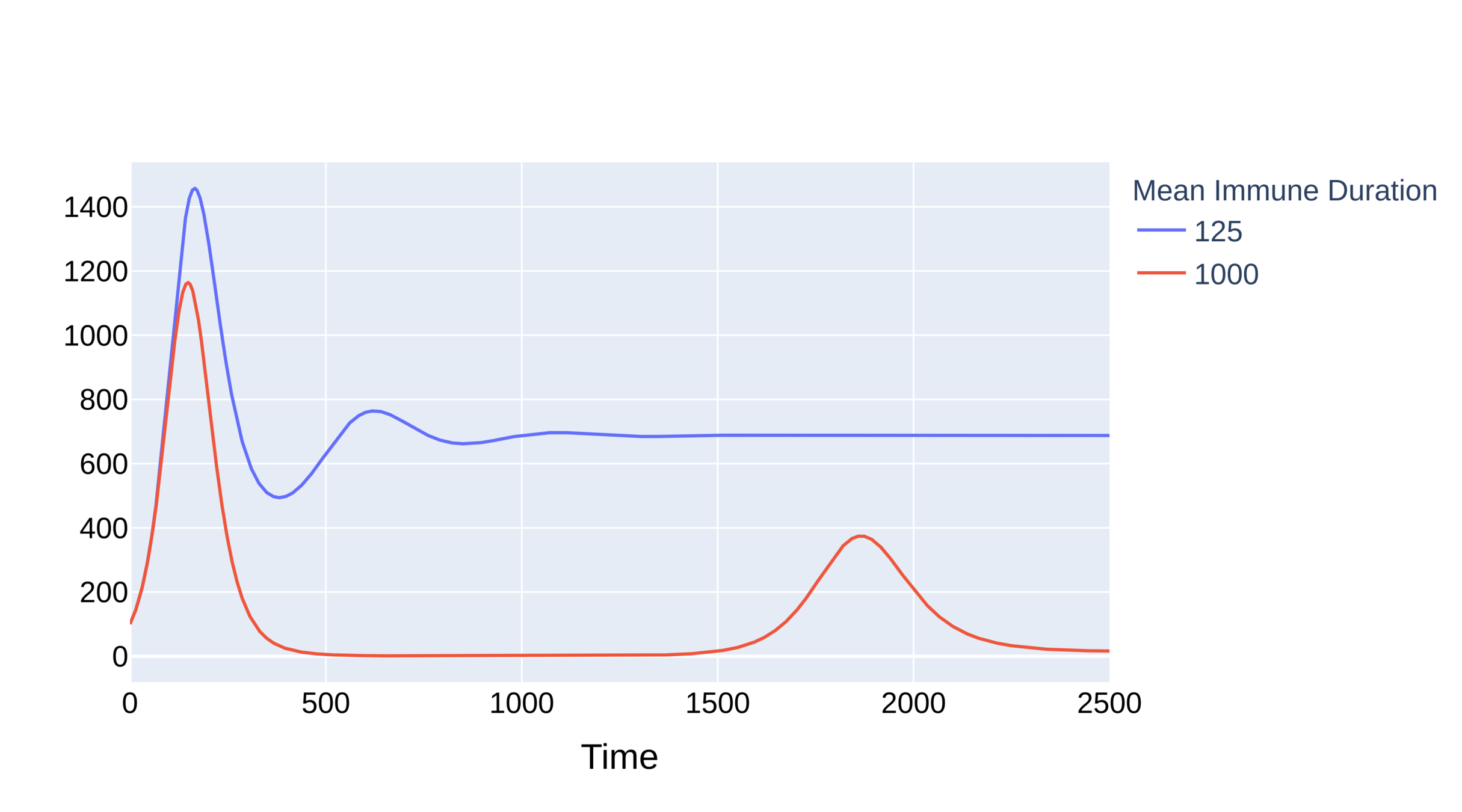
Temporary immunity:

Two types of supercriticality

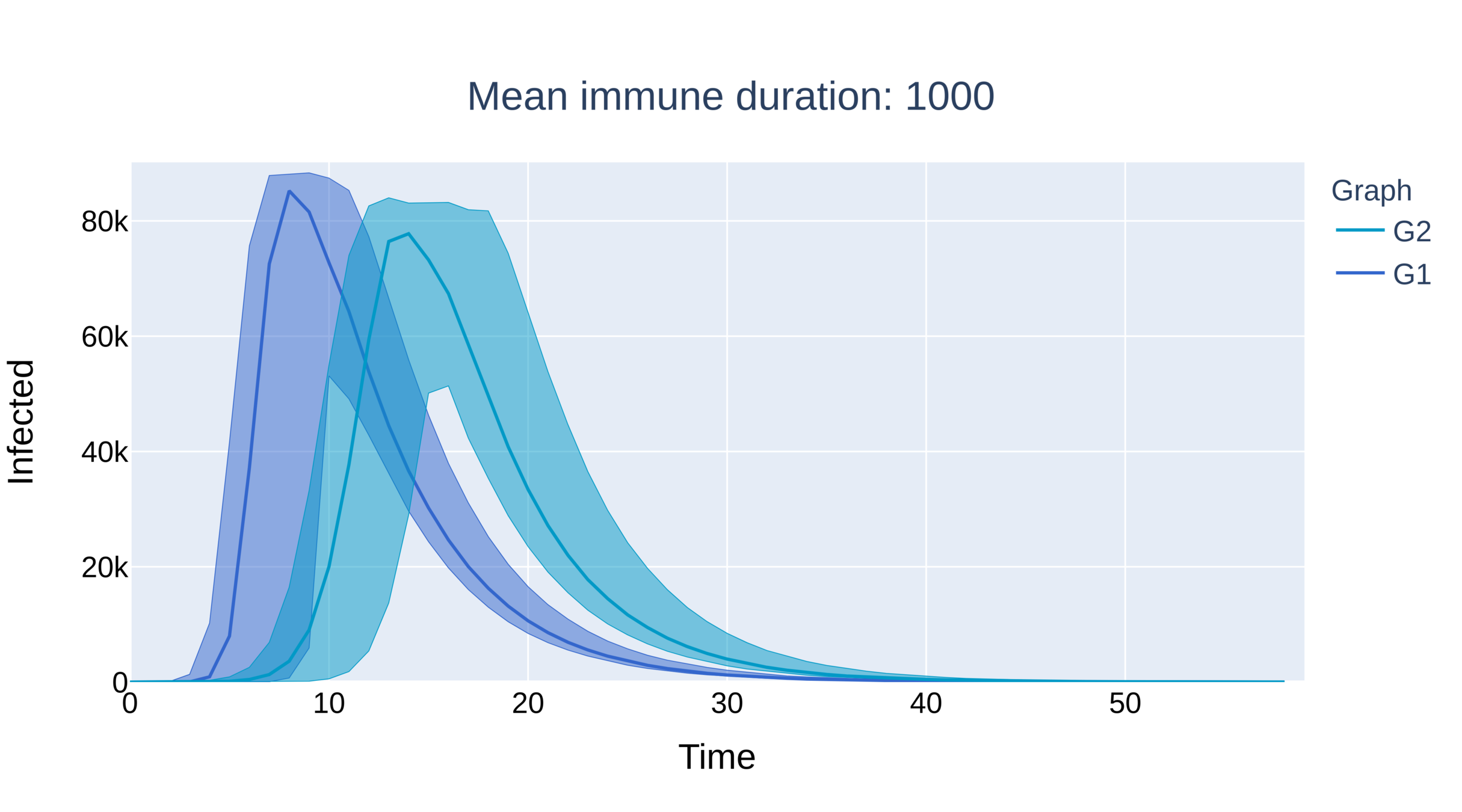
Parameters:

\(\beta=.225\),

\(\gamma=.2\)

mean deg. \(\approx 9\)

\(\tau>3\)

\(\tau\in(2,3)\)

Modeling interventions: remove edges

  • Remove edges before start epidemic
     
  • Resulting epidemic still supercritical
     
  • "Rule" per intervention strategy:
    • Social dist.: Random
    • No travel: Long edges
    • No hubs: Removing edges from large-degree nodes
       
  • Match intervention parameters s.t. average degree after intervention is comparable (approx. 60% edges remain)

No interv.

Social dist.

No travel

No hubs

No travel works best for  the first peak

Graph with power-law exponent \(\tau>3\)

  • Travel restrictions bring down first peak, but elongate the outbreak
     
  • Absence of long-range edges: Average graph distance increases from logarithmic to polynomial in network size
     
  • First peak insensitive for immunity
     
  • Similar figure for graph G1 (\(\tau\in(2,3)\))

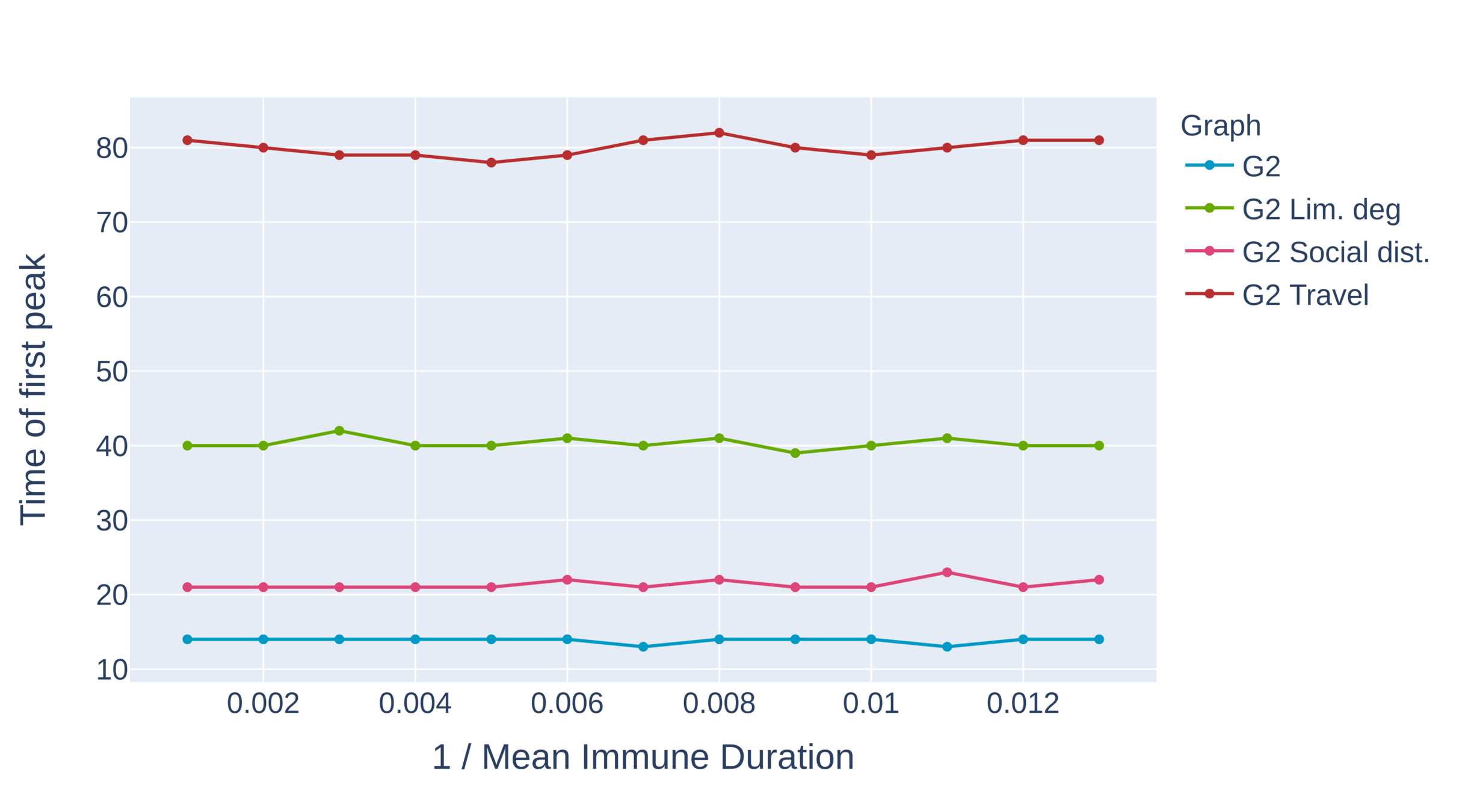
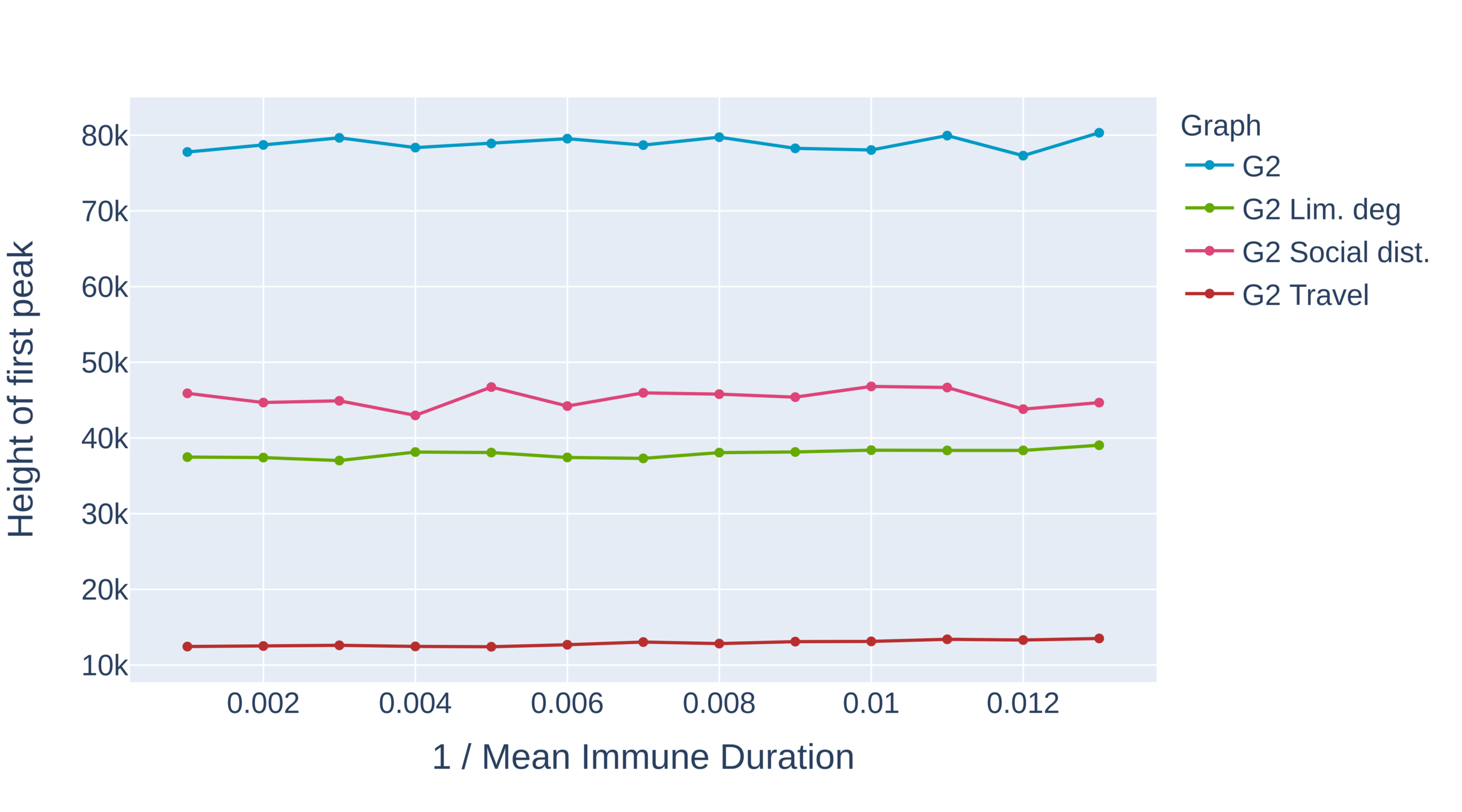
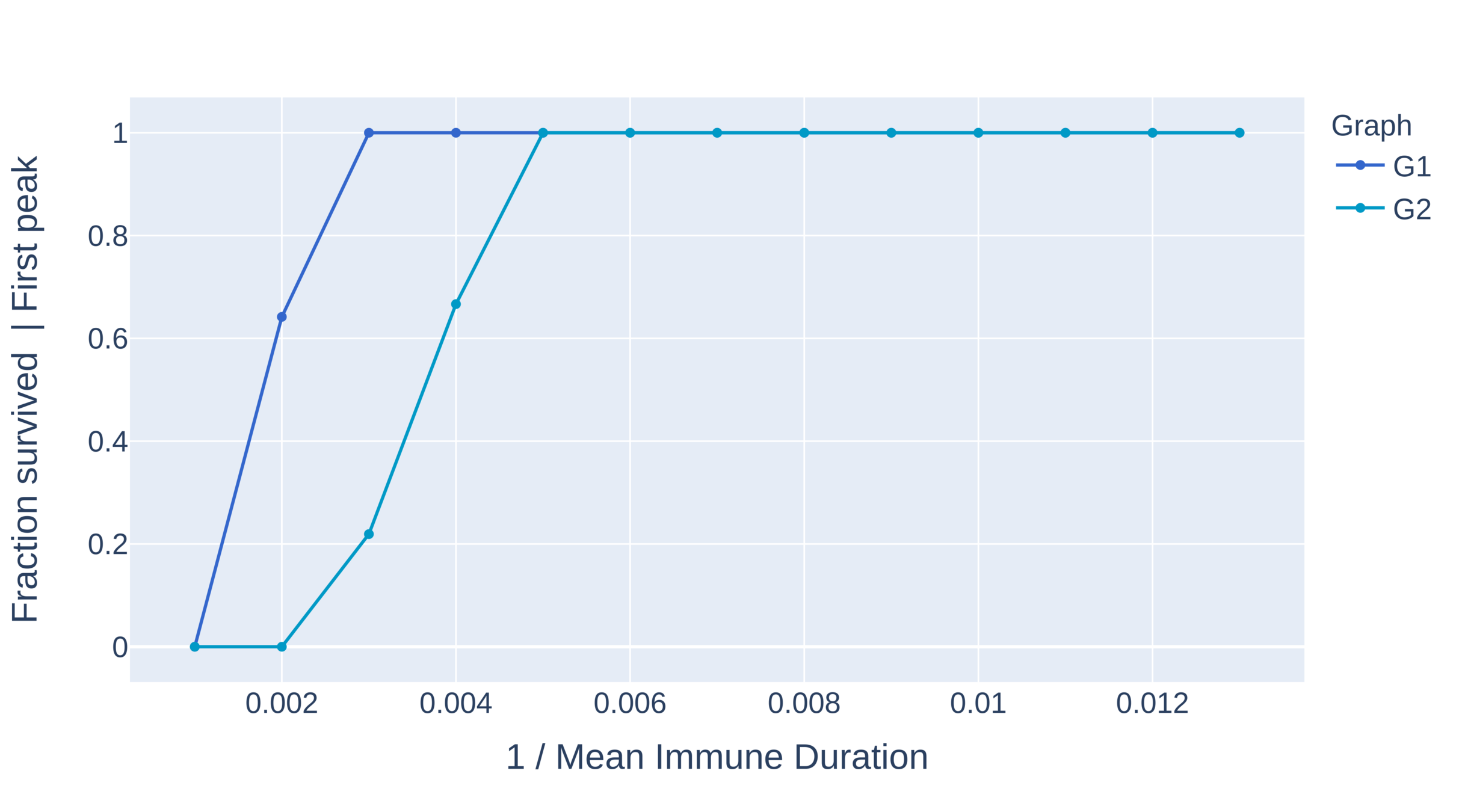
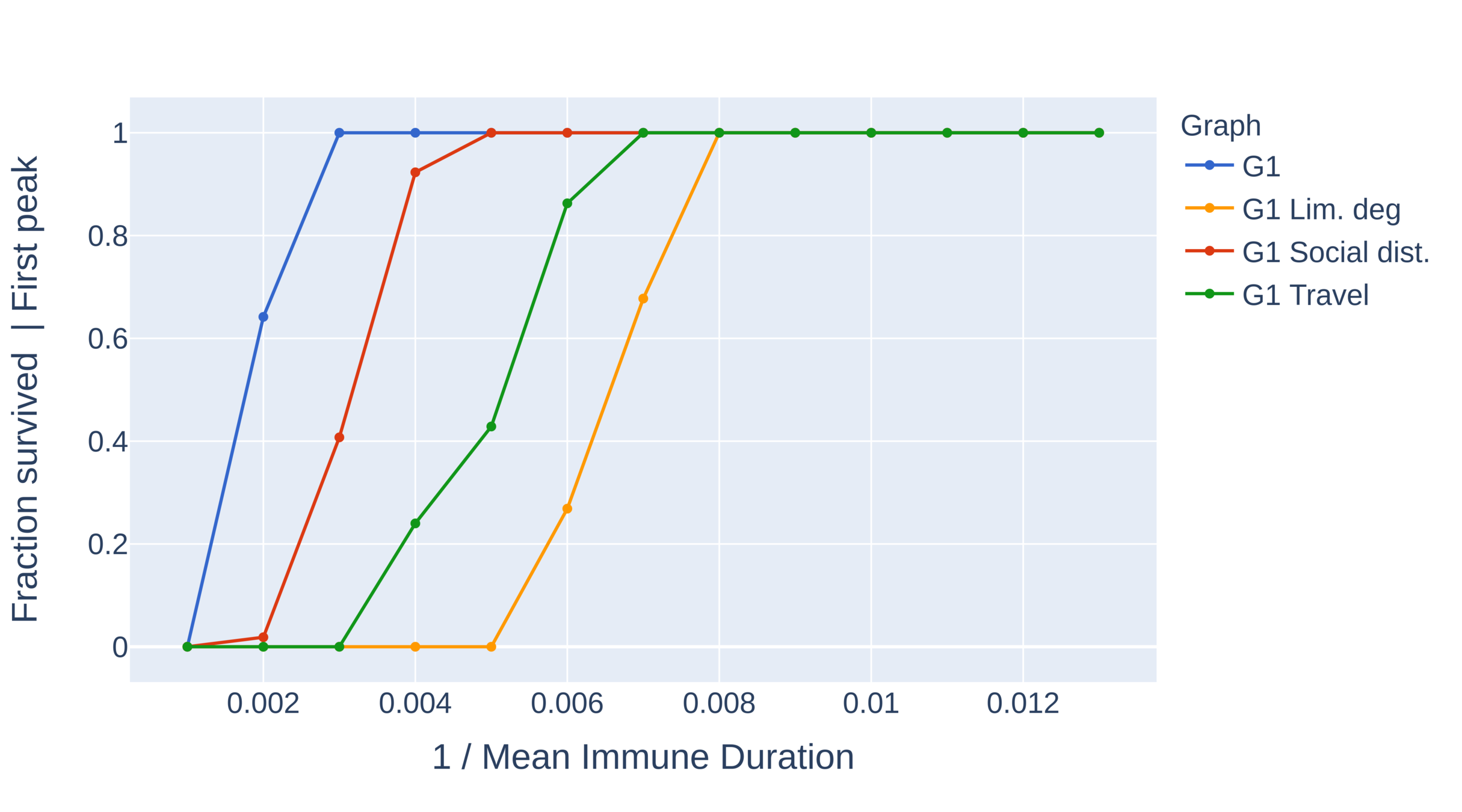
Critical immune duration decreases under interventions (I)

Graph with power-law exponent \(\tau>3\)

  • Critical immunity length is shortest under limitation of degree and travel restrictions.

     
  • Absence of hubs: larger oscillations
     
  • First peak for travel restrictions is as high as second peak under degree limitation

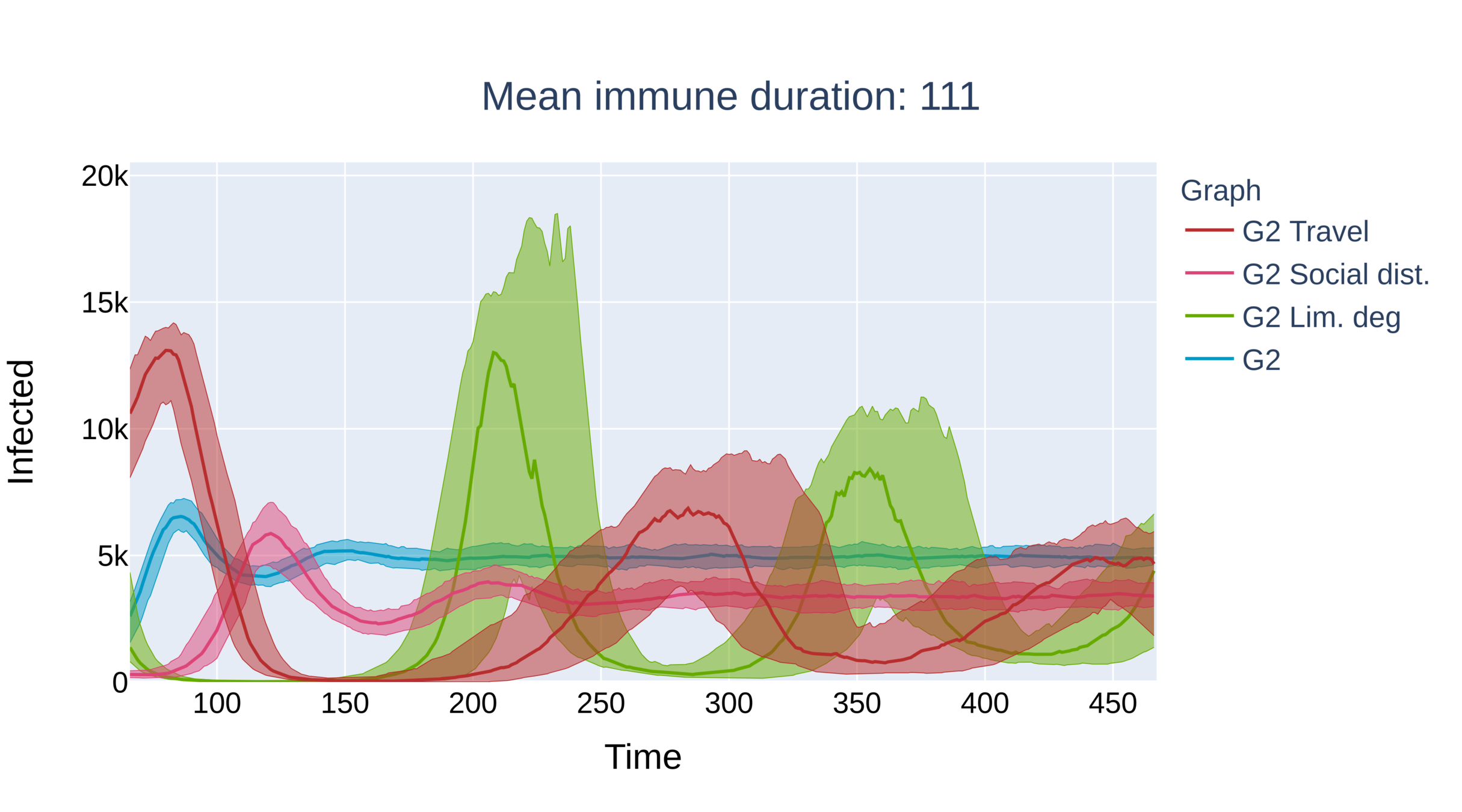
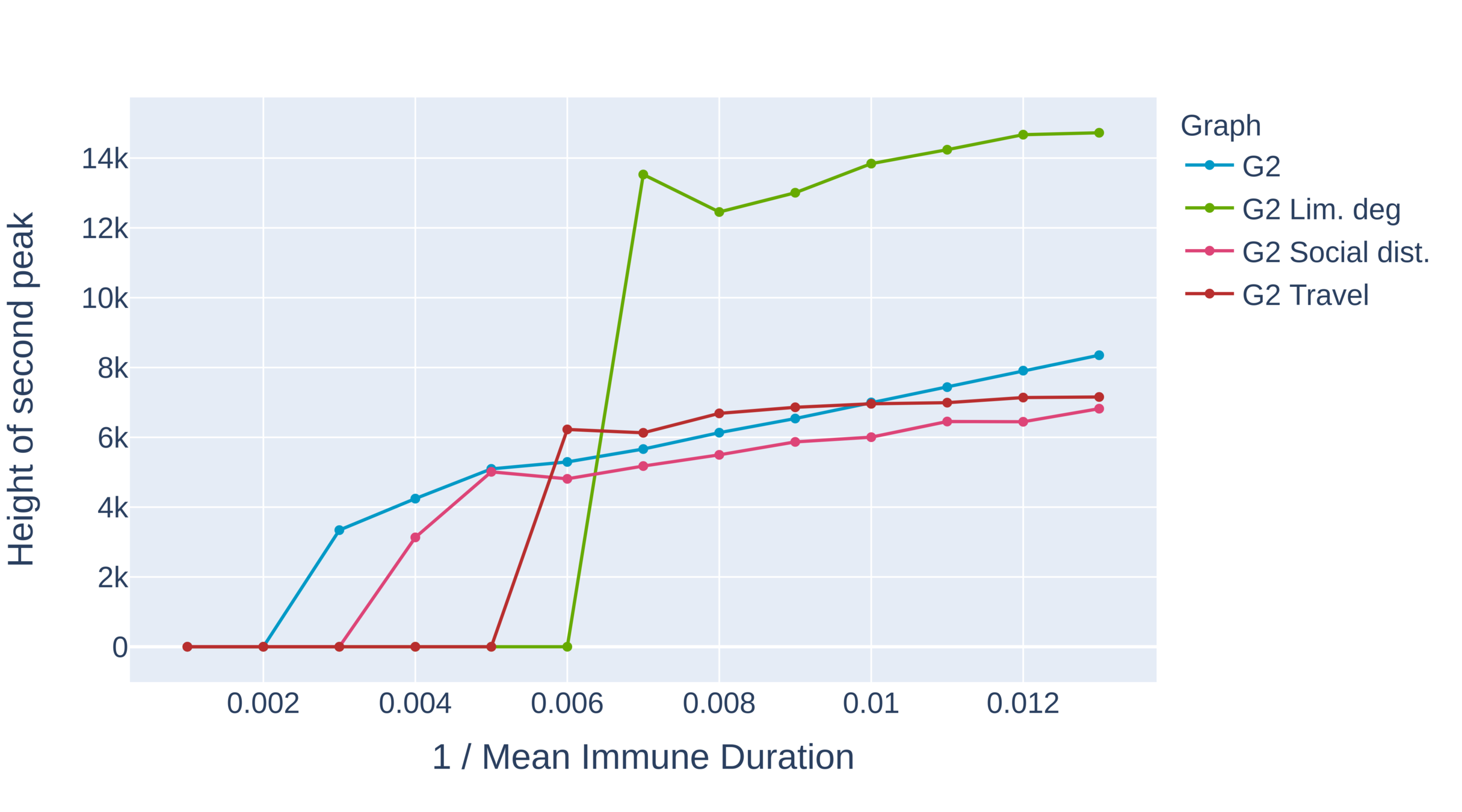
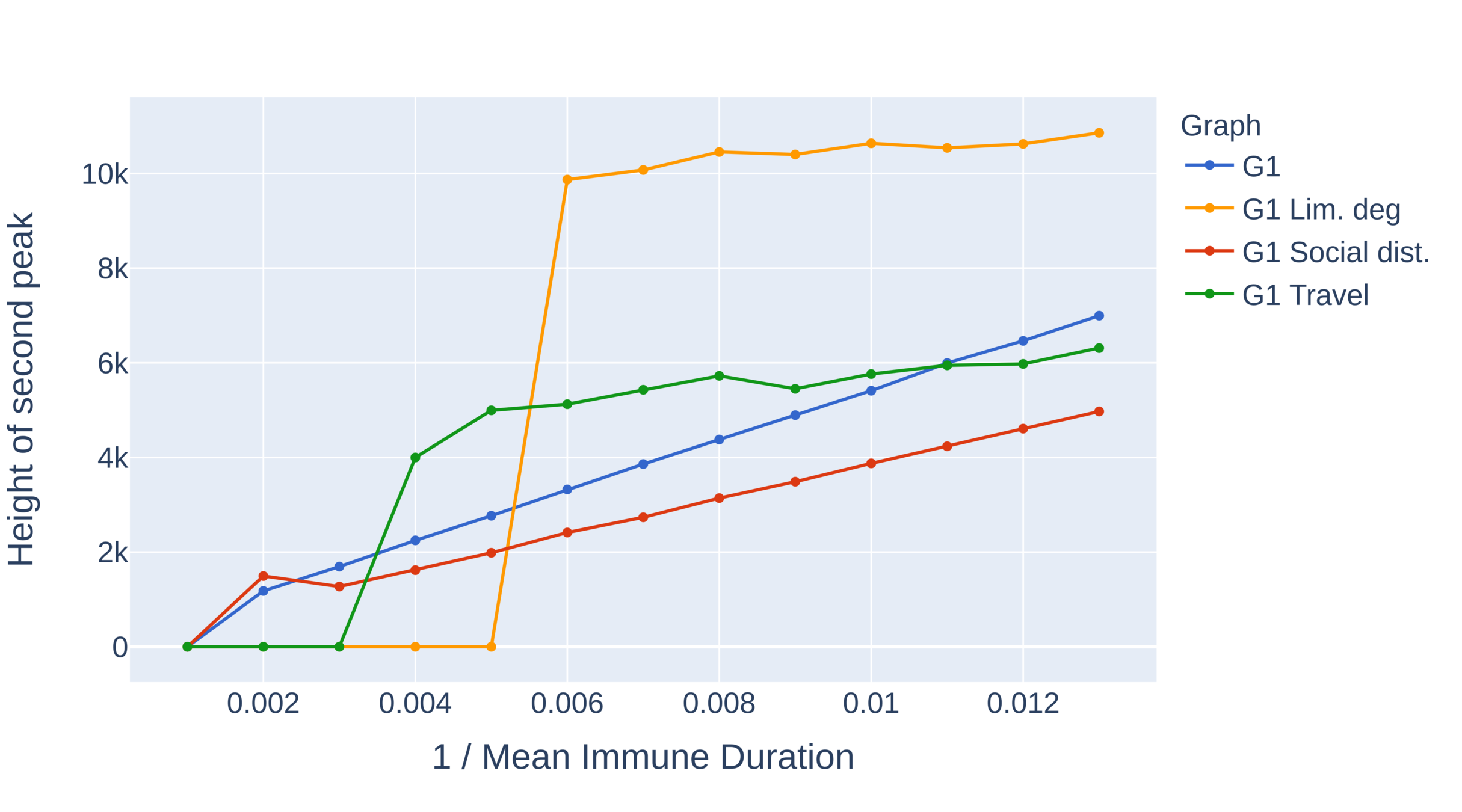
Critical immune duration decreases under interventions (II)

Graph with power-law exponent \(\tau\in(2,3)\)

  • Without intervention the system immediately equilibriates.
     
  • Critical immunity length is smallest under limitation of degree, travel restrictions outperform social distancing.
     
  • No oscillations for social distancing. Presence of larger hubs brings the system to equilibrium quicker.
     

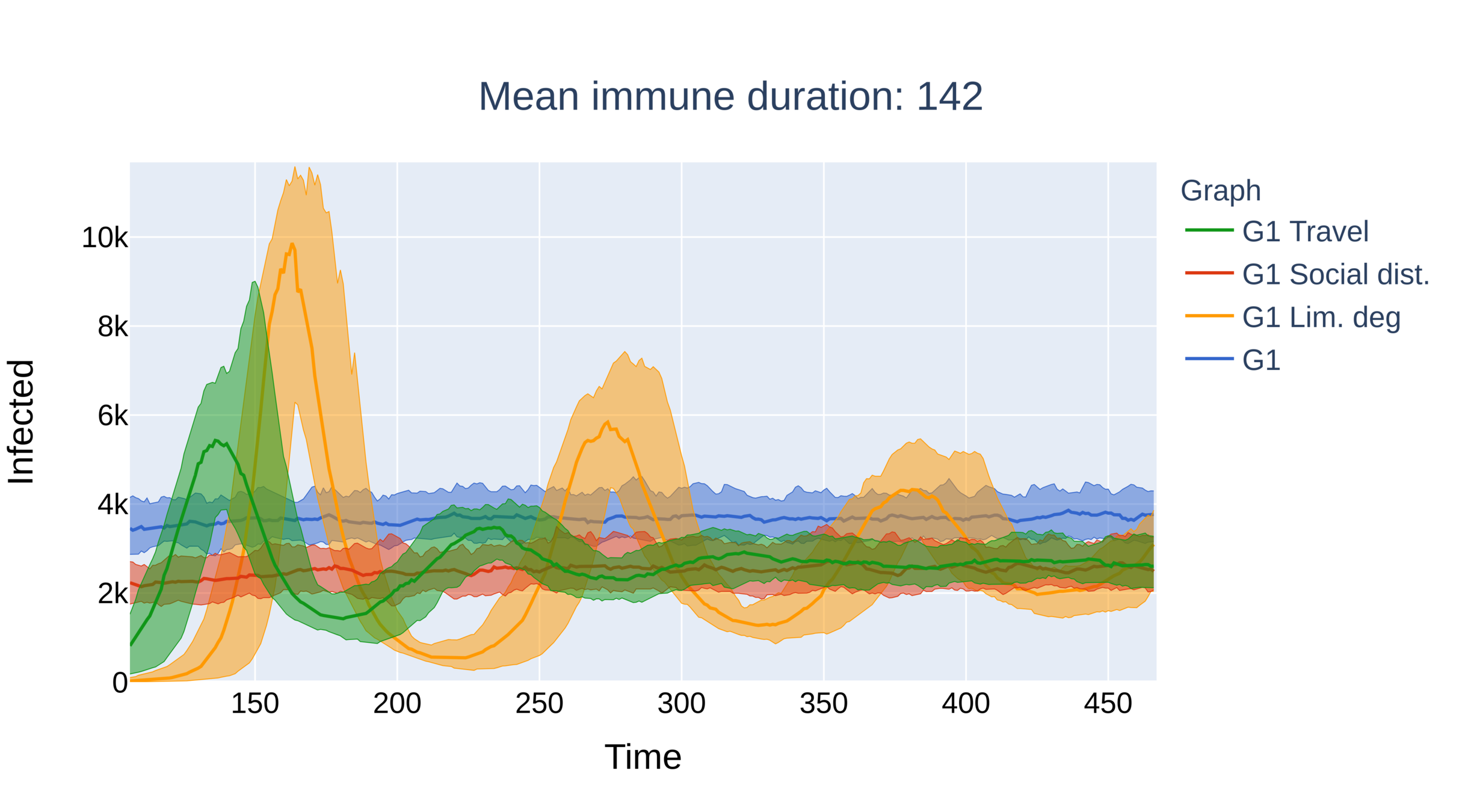
Main conclusions

  • Epidemics on networks with underlying geometry show richer behaviour than compartmental models.
  • Network topology plays a profound role.
  • Networks allow for intuitive modeling of interventions.
    • Travel restriction works best but they elongate epidemic.
    • Limiting node degree might result in high second peak

 

Thank you for your attention!

https://arxiv.org/abs/2005.06880

Long survival probability under interventions

Higher degree-spread diminishes amplitude

No travel works well for later peaks

Higher degree-spread diminishes amplitude

No travel works well for later peaks

Higher degree-spread diminishes amplitude

Compartmental model

  • Additional states could be added
  • "Mean-field" model: everything is averaged out:
    individuals are equal, everybody is weakly connected, individuals are "real-valued"
     
  • Only way of modeling interventions:
    Set \(\beta:=\beta(t), \gamma:=\gamma(t), N:=N(t)\).
  • Unclear how and why interventions work
  • What is the most effective intervention?

Susceptible

Infected

Recovered

\beta \frac{I(t)S(t)}{N}
\gamma

Network-based approach

Susceptible

Infected

Recovered

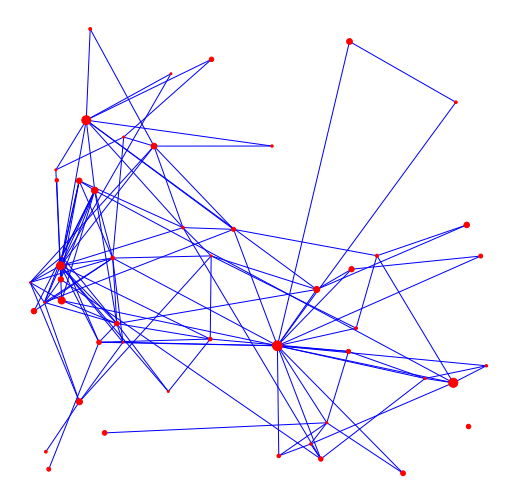
Infect neighbor w.p. \(\beta\)

Heal w.p. \(\gamma\)

  • Contact network as a graph
  • Infectious nodes infect  neighbors
  • Models "coincide" for complete graph and scaling \(\beta\)
     
  • Interventions: remove edges

Network-based approach

Susceptible

Infected

Recovered

Heal w.p. \(\gamma\)

  • Contact network as a graph
  • Infectious nodes infect  neighbors
  • Models "coincide" for complete graph and scaling \(\beta\)
     
  • Interventions: remove edges
    • At random (social dist.)

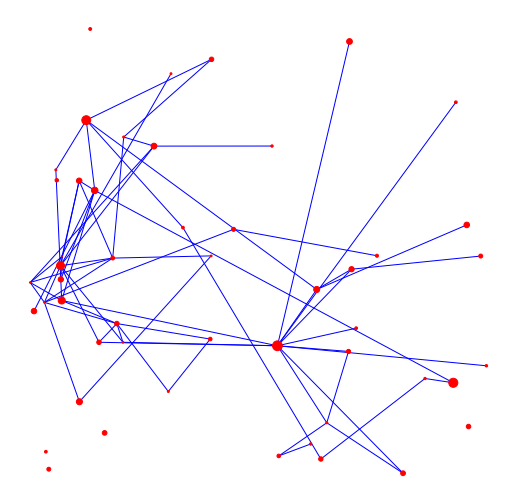
Infect neighbor w.p. \(\beta\)

Network-based approach

Susceptible

Infected

Recovered

Heal w.p. \(\gamma\)

  • Contact network as a graph
  • Infectious nodes infect  neighbors
  • Models "coincide" for complete graph and scaling \(\beta\)
     
  • Interventions: remove edges
    • At random (social dist.)
    • Euclidean length (no travel)

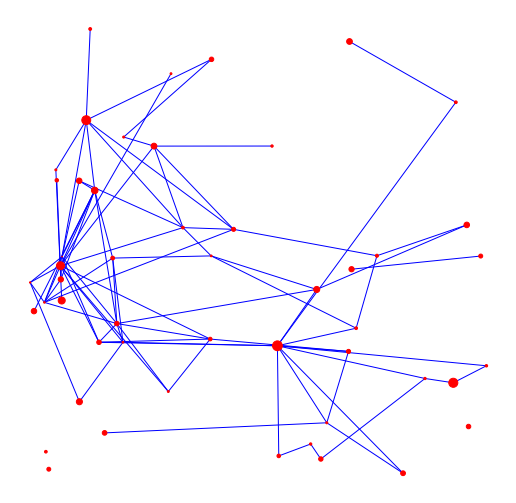
Infect neighbor w.p. \(\beta\)

Network-based approach

Susceptible

Infected

Recovered

Heal w.p. \(\gamma\)

  • Contact network as a graph
  • Infectious nodes infect  neighbors
  • Models "coincide" for complete graph and scaling \(\beta\)
     
  • Interventions: remove edges
    • At random (social dist.)
    • Euclidean length (no travel)
    • Degree (limit # contacts)

Infect neighbor w.p. \(\beta\)

ODE approach

Susceptible

Infected

Recovered

Infect neighbor w.p. \(\beta\)

Heal w.p. \(\gamma\)

Susceptible w.p. \(\eta\)

  • Immunity unclear for COVID-19
  • Natural model for "second" peaks

Network approach

Network topology

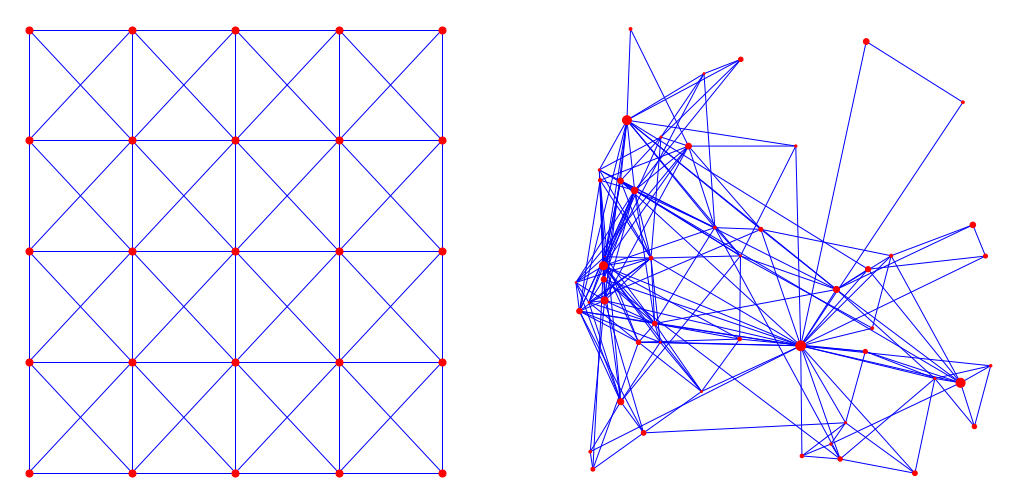
Two graphs with mean degree 8

Network approach

Network topology

Mean degree 8, 160000 nodes

Network approach

Network topology

Two graphs with mean degree 8

Polynomial growth

"Faster" growth

Network approach

Network topology

Desired features

  • "close" nodes are
    likely to be connected
  • High variability in degrees
  • "Important" nodes are
    likely to be connected

 

Random graph model (\(\alpha>1\)):

 

p_{ij} \approx c\Big(\frac{W_iW_j}{\|x_i-x_j\|^2}\Big)^\alpha

Results

  • Network vs. Compartmental
    • New phases
    • Oscillations
  • Effect of social dist., no travel, no hubs
    • How to compare?
    • First peak
    • Later peaks
    • Probability of survival

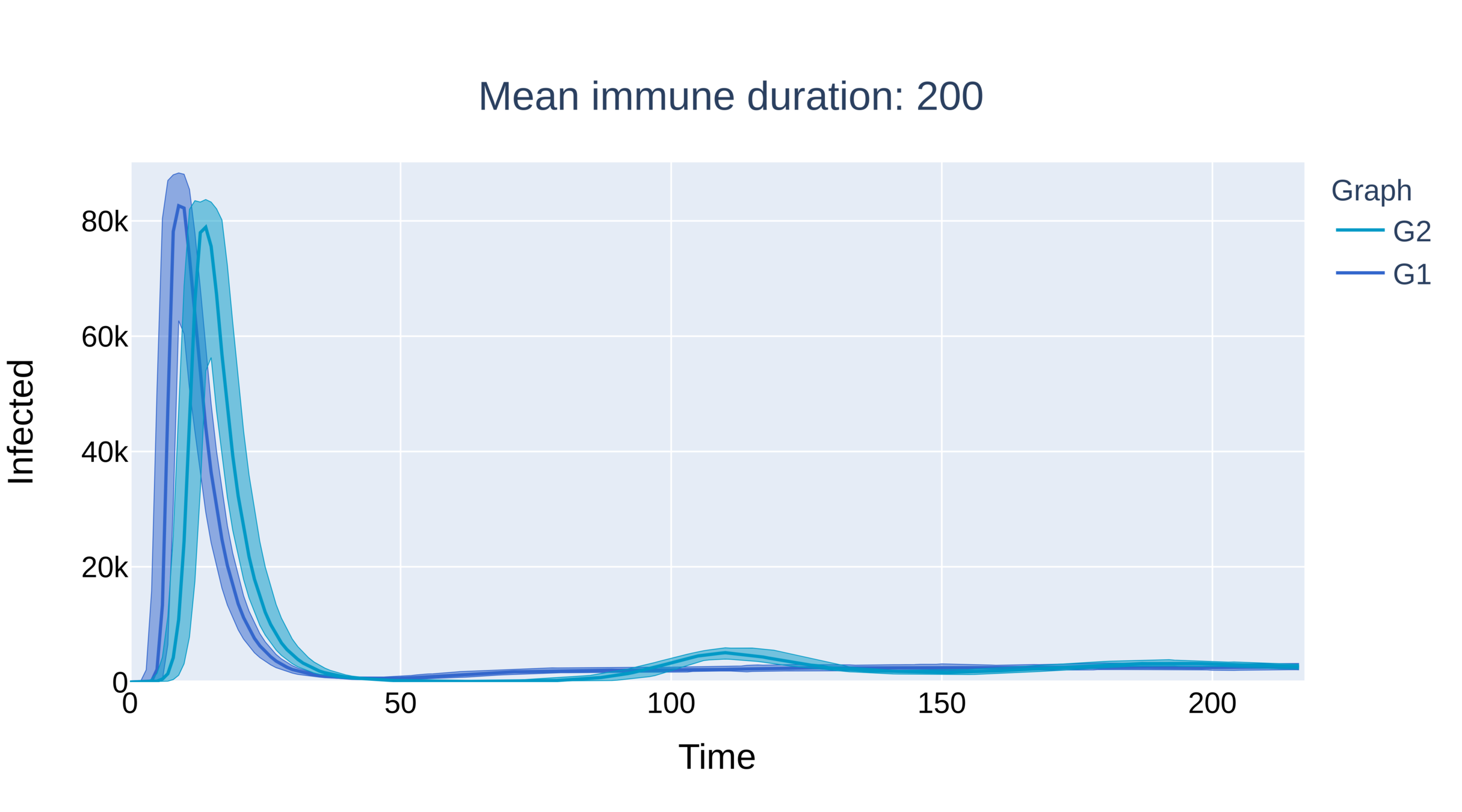
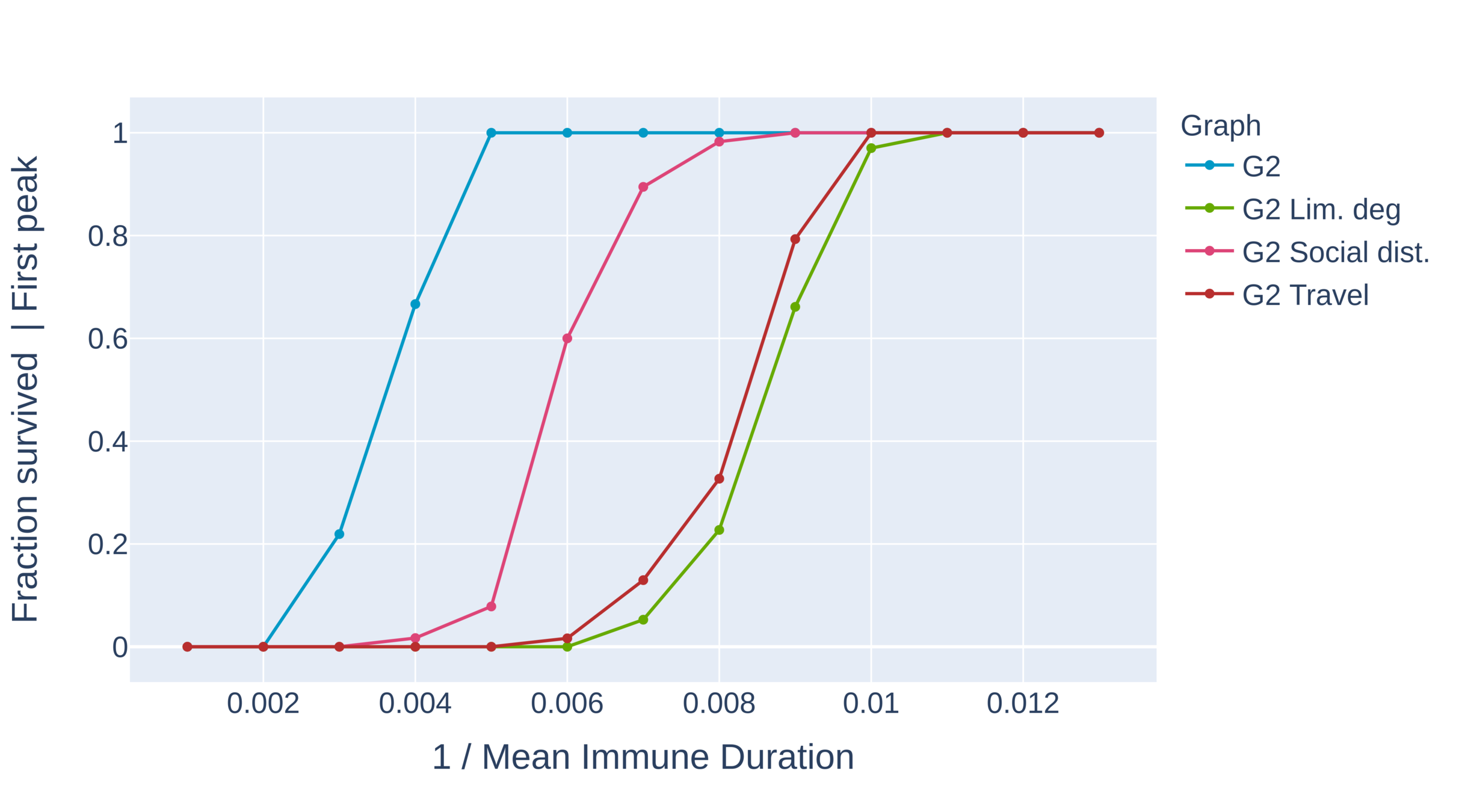
Supercritical epidemic dies out in network for \(\eta\) small

Single peak, extinction

large graphs, 100 runs

Survival

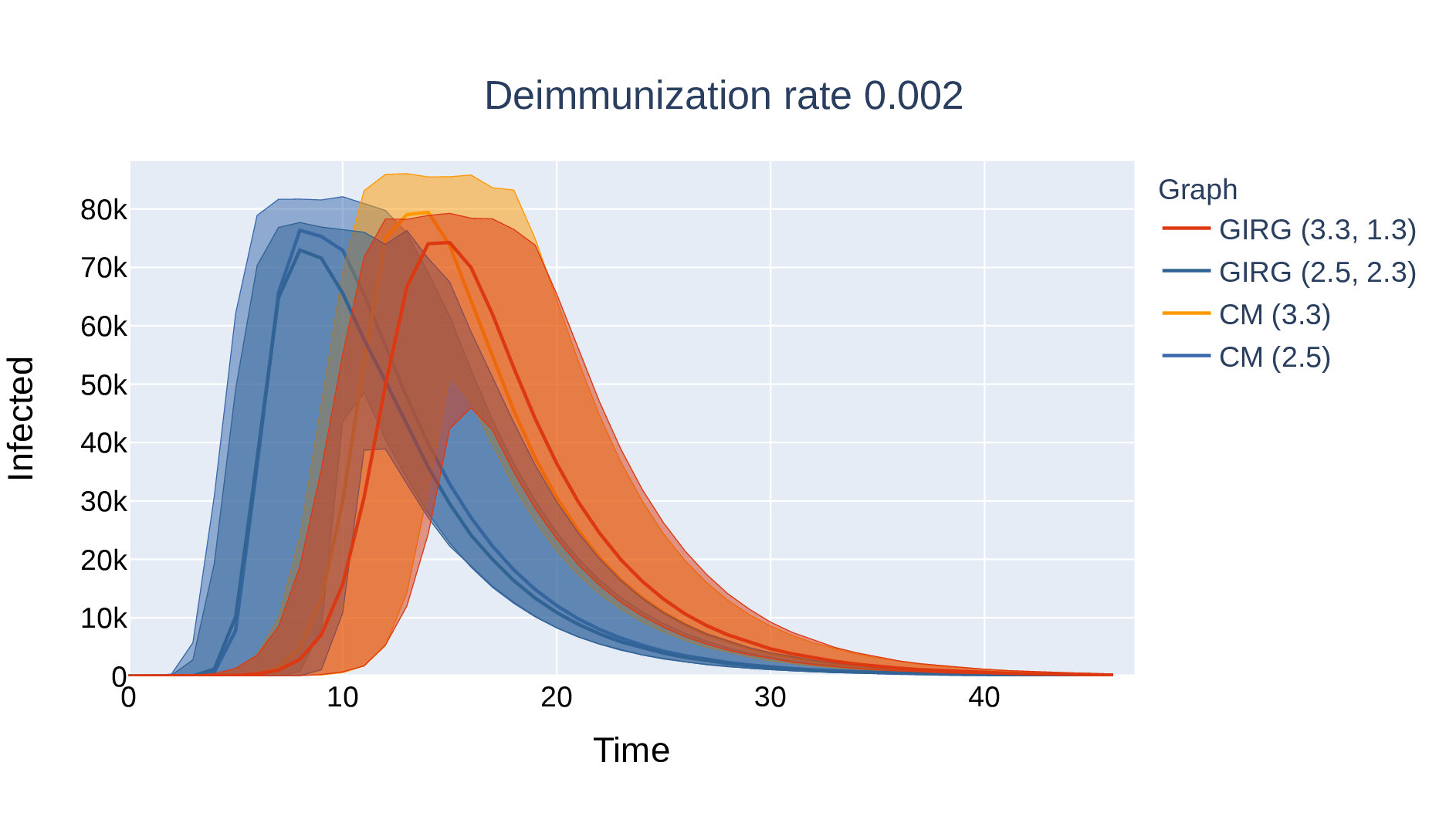
Four networks

Compartmental,

\(\eta\) small and large

Geometry introduces "immunity boundaries", herd immunity

Supercritical epidemic can survive in network for \(\eta\) large

Four networks

Compartmental,

\(\eta\) small and large

Single peak, survival

large graphs, 100 runs

Survival

Supercritical epidemic can survive in network for \(\eta\) large

Oscillations in three networks

Absence of long edges: larger amplitude

Results

  • Network vs. Compartmental
    • New phases
    • Oscillations
  • Effect of social dist., no travel, no hubs
    • How to compare?
    • First peak
    • Later peaks
    • Probability of survival
Made with Slides.com