Copy of Introduction

Spatial random graphs with tunable assortativity

Joost Jorritsma

joost.jorritsma@stats.ox.ac.uk

Intriguing maths: classical network models

Erdős–Rényi random graph $G(n, \lambda /n)$

Bernoulli percolation on $\mathbb{Z}^2$ w.p. $p$

Intriguing maths: classical network models

Motivation

Do there exist graphs with property X?
Is there a percolation phase transition?
What happens at the critical point?
What is the component-size distribution?

Intriguing maths: classical network models

Motivation

Universality: do all network (models) behave like ...?
What are the implications for real-world networks?

Aim for this talk

Introduce model for type-1 question
Give modelling interpretation: degree assortativity
Is this model useful for applications?
What should we investigate?

Intriguing maths: classical network models

Motivation

Universality: do all network (models) behave like ...?
What are the implications for real-world networks?

Aim for this talk

Introduce model for type-1 question
Give modelling interpretation: degree assortativity
Is this model useful for applications?
What should we investigate?

\kappa_\mathrm{prod}=w_uw_v

\alpha\in(1,\infty], d\ge 1

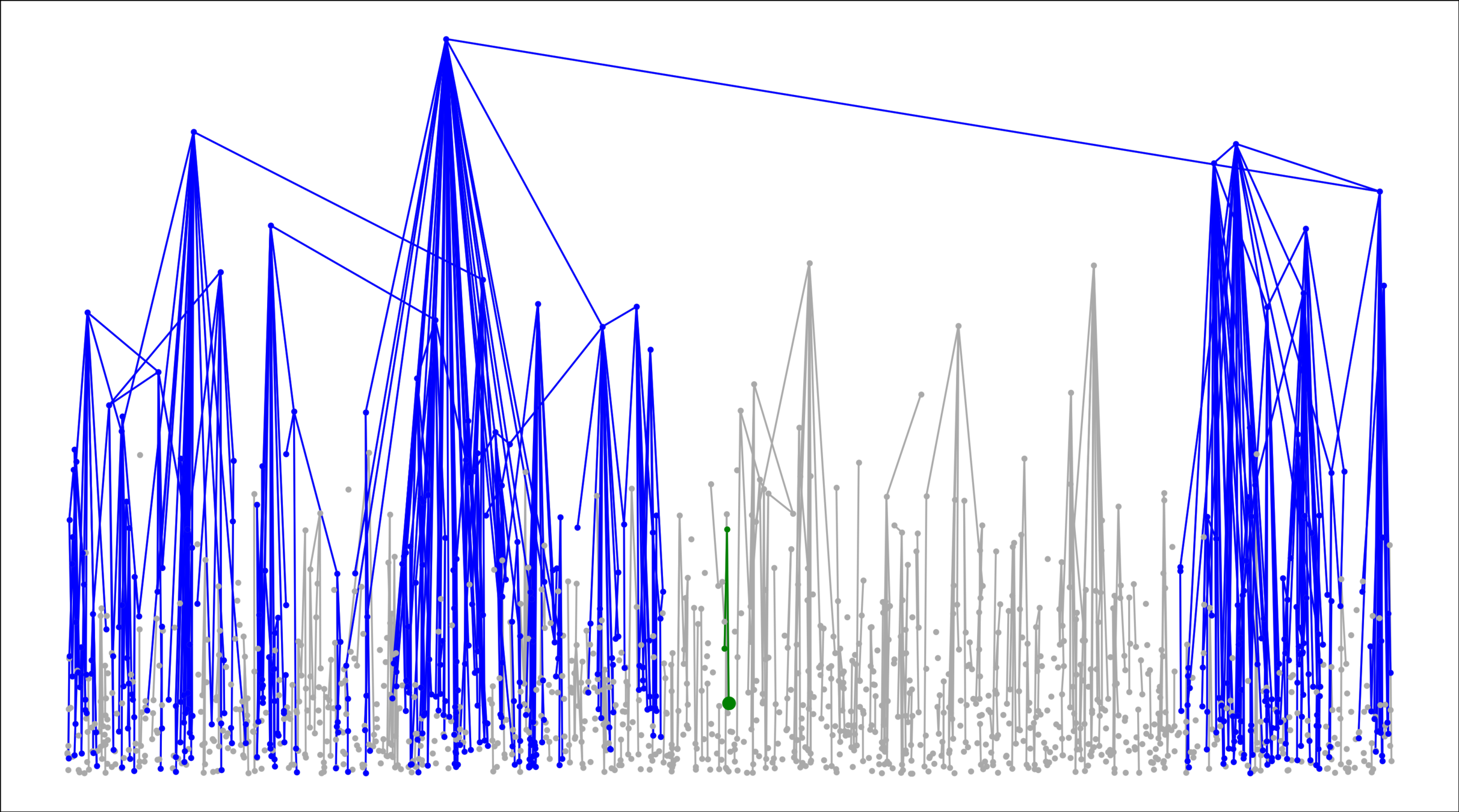
Geom. Inhom. RG

\kappa_\mathrm{prod}=w_uw_v

\alpha=\infty, d= 1

Hyperbolic RG

Geom. RG

\kappa_\mathrm{triv}\equiv 1

\alpha=\infty, d \ge 2

Long-range perc.

\kappa_\mathrm{triv}\equiv 1

\alpha\in(1,\infty), d\ge 1

\kappa_{\max}=w_u\vee w_v

Scale-free Gilbert RG

\kappa_{\mathrm{pa}}=(w_u\vee w_v)

\cdot(w_u\wedge w_v)^{\tau-2}

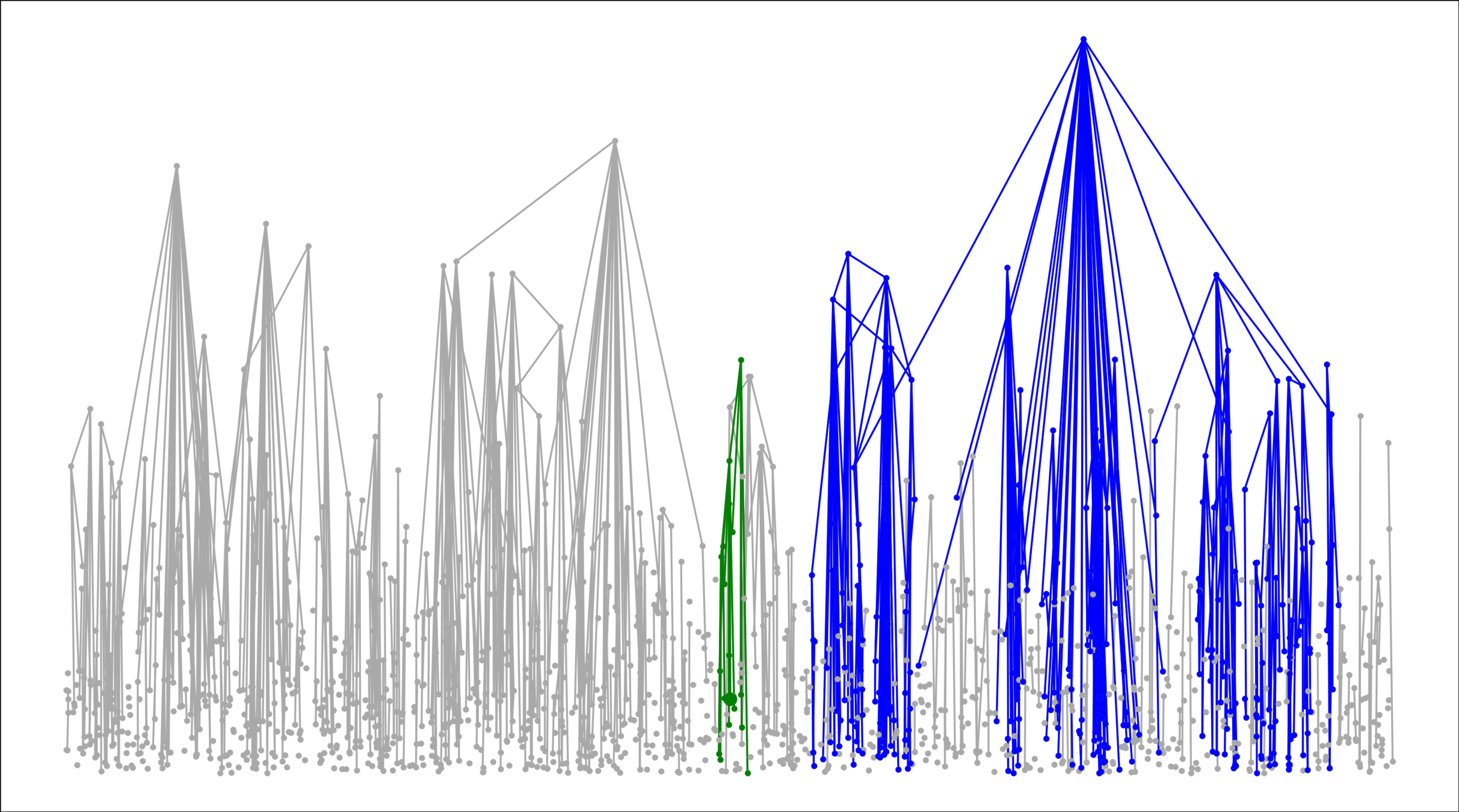
Age-dependent RCM

Theorem. When $\tau<2$ or $\alpha<1$:

Infinite degrees
Bounded diameter

[Deijfen, v.d. Hofstad, Hooghiemstra '13], [Gracar, Grauer, Lüchtrath, Mörters '18]

[Heydenreich, Hulshof, J. '17], [Hirsch '17], [v.d. Hofstad, v.d. Hoorn, Maitra '22],

[J., Komjáthy, Mitsche, '23], [Lüchtrath '22]

Theorem. When $\tau>2$ and $\alpha>1$:

$$\mathbb{P}(\mathrm{deg}(0)\ge k)\sim k^{-(\tau-1)}.$$

$\tau$ small: many hubs

$\alpha$ small: many long edges

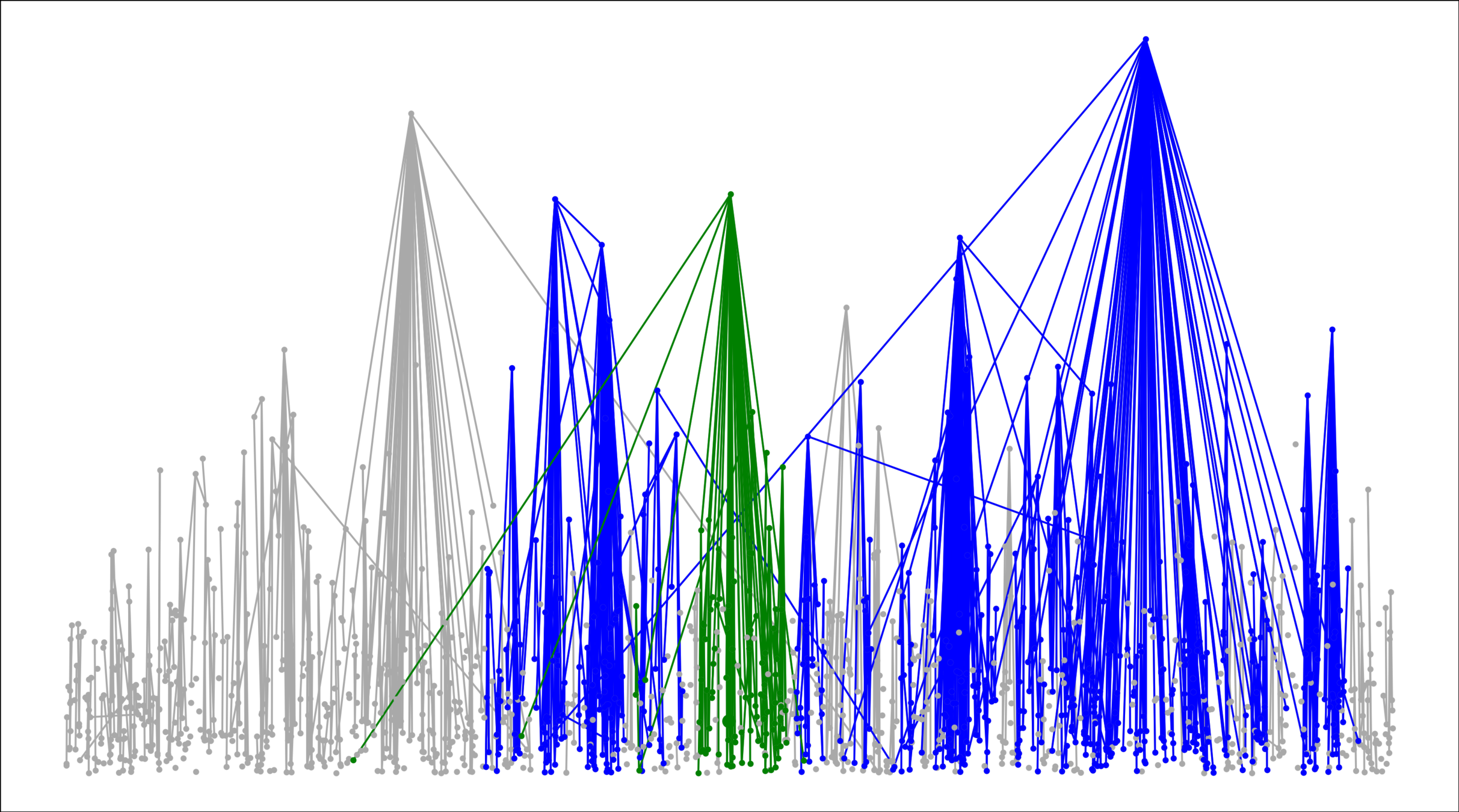
Hyperbolic random graph

Scale-free percolation

Long-range percolation

Scale-free Gilbert RG

Random geom. graph

Nearest-neighbor percolation

Kernel-based spatial random graphs

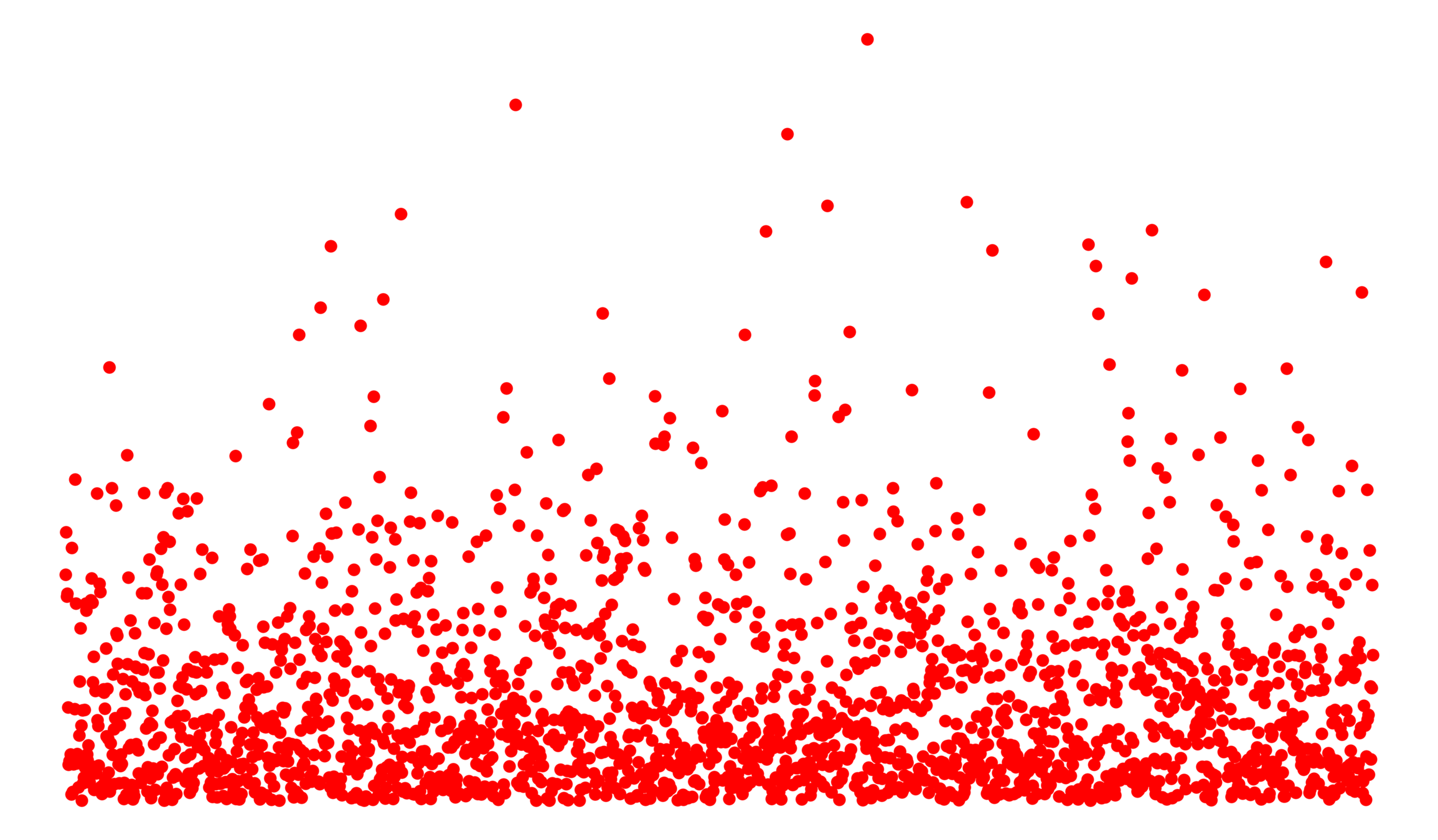
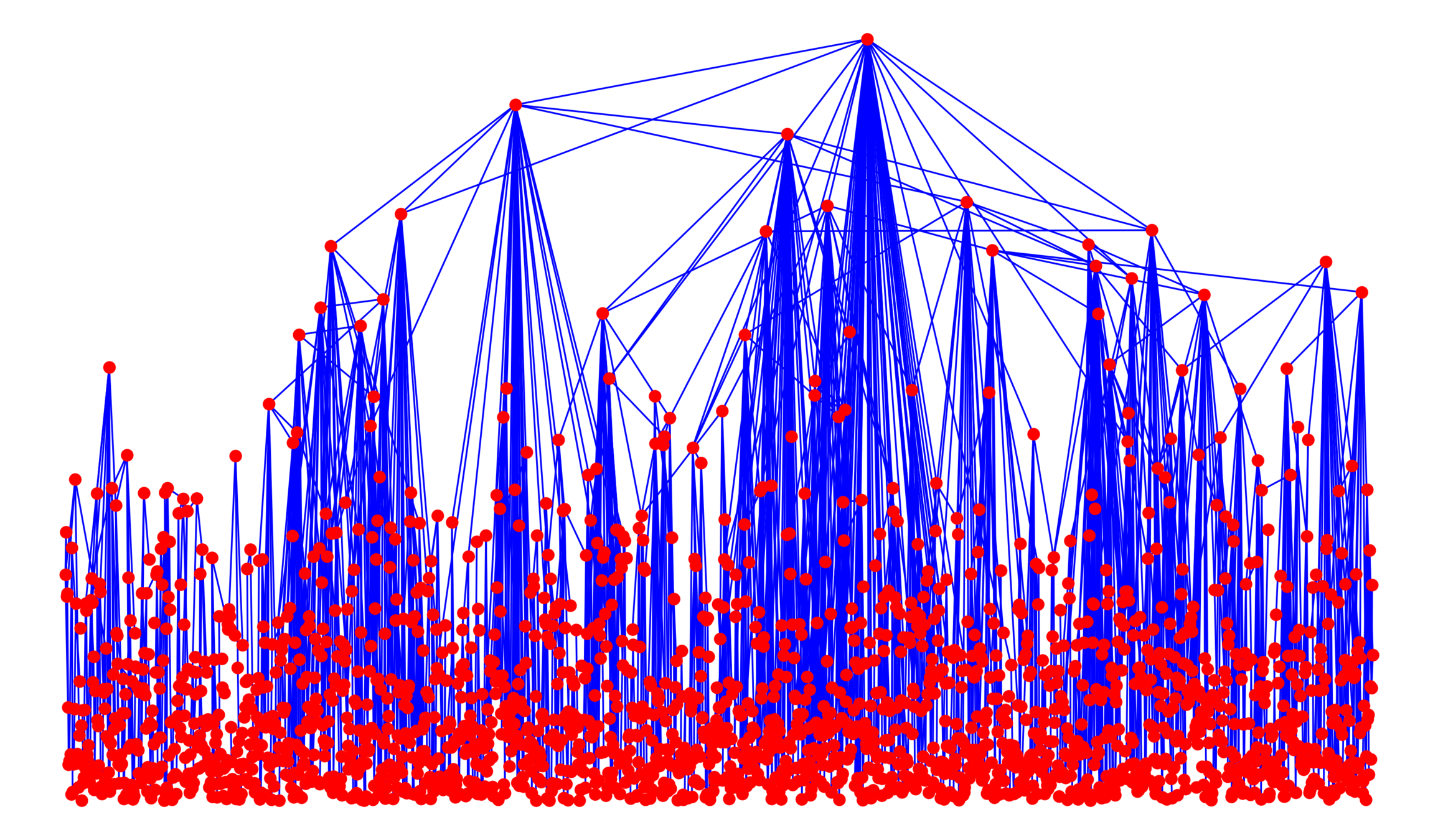
Edge set $\mathcal{E}_\infty$

Long-range parameter $\alpha>1$,
Edge-density $\beta>0$,
Percolation $p\in(0,1]$

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{\beta\cdot \phantom{(w_u\cdot w_v)}}{\|x_u-x_v\|^d}\wedge 1\bigg)^\alpha$$

Vertex set $\mathcal{V}_\infty$

Spatial locations, either
- Lattice $\mathbb{Z}^d$
- Poisson point process (unit intensity)
Power-law i.i.d. weights $w_v\ge 1$:
$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$,

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\frac{\beta\cdot (w_u\cdot w_v)}{\|x_u-x_v\|^d}\wedge 1\bigg)^\alpha$$

The interpolating kernel

Connection probability

$${\color{grey}\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta}\frac{\kappa(w_u, w_v)}{\color{grey}\|x_u-x_v\|^d}{\color{grey}\bigg)^\alpha\wedge 1}$$

A parameterized kernel: $\sigma\ge 0$

$$\kappa_{\sigma}(w_u, w_v):=\max\{w_u, w_v\}\min\{w_u, w_v\}^\sigma$$

$\tau: \mathbb{P}(w_v\ge w)=w^{-(\tau-1)}.$
$\sigma$: assortativity
$\sigma$: interpolation

\frac{\sigma}{\tau-1}

\frac1{\tau-1}

1

\sigma=\tau-1

\tau=2

\sigma=1

\sigma=\tau-2

\sigma=0

SFP/GIRG

Hyperbolic RG

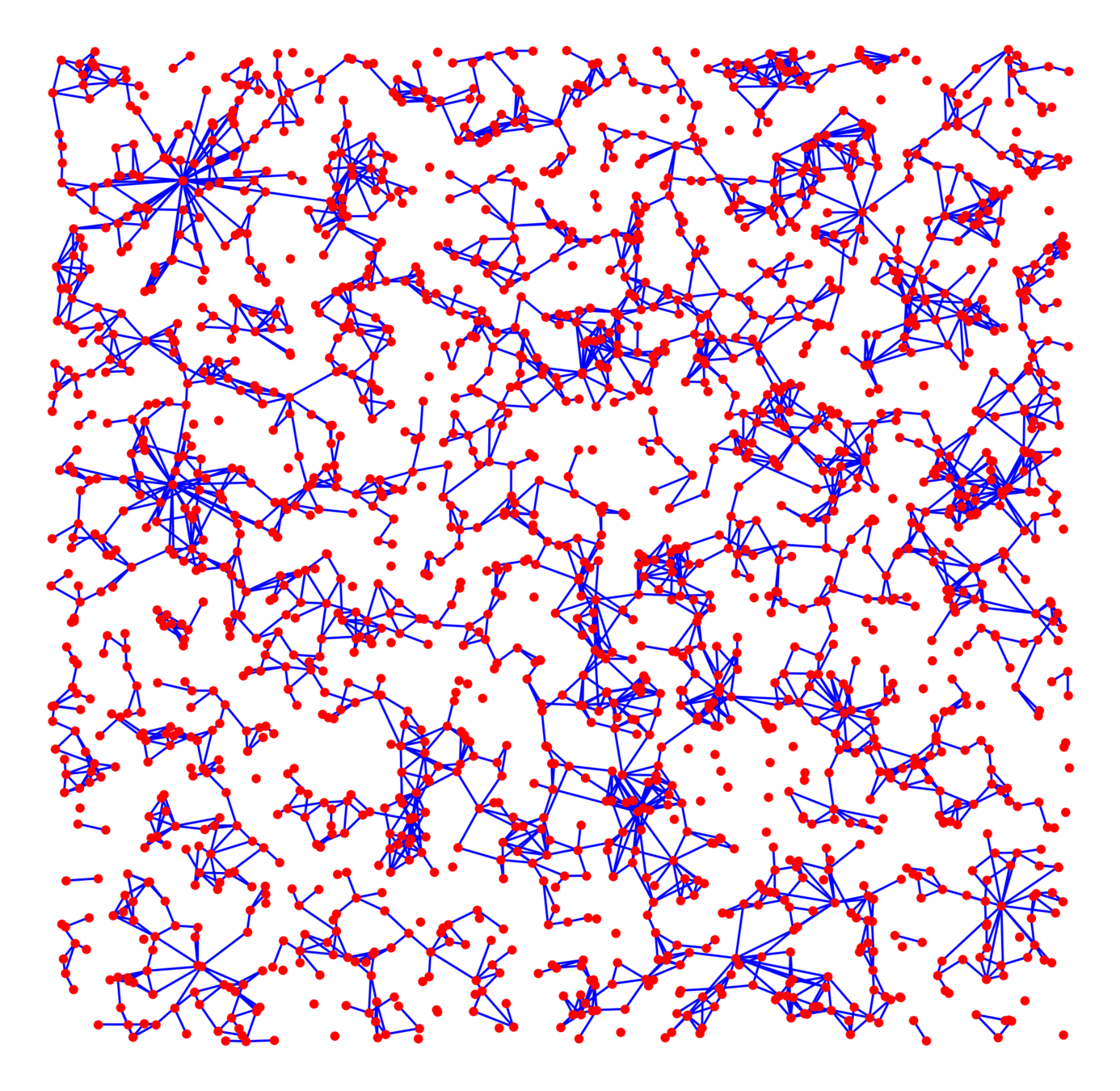
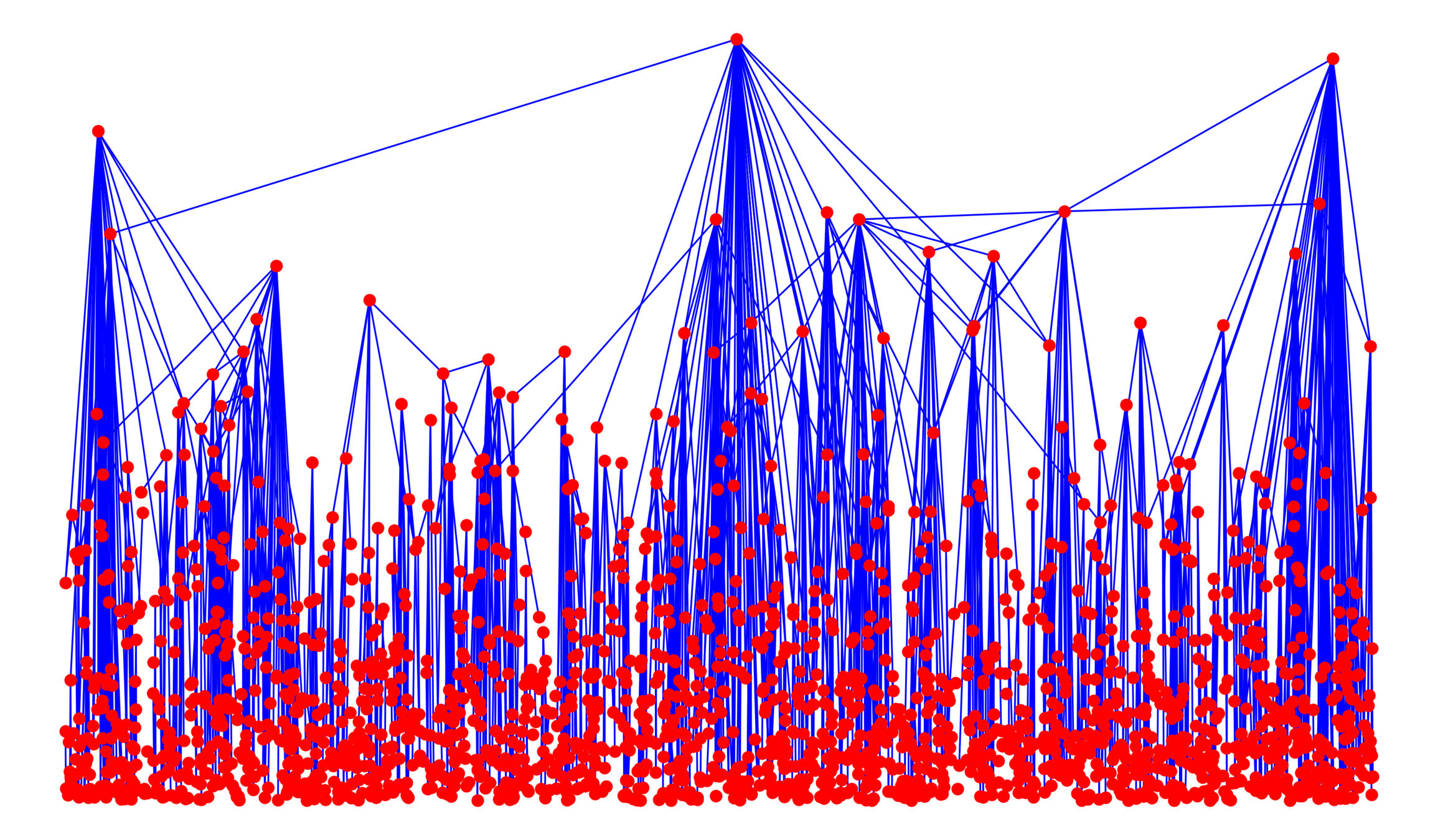
Age-dep. RCM

Scale-free Gilbert

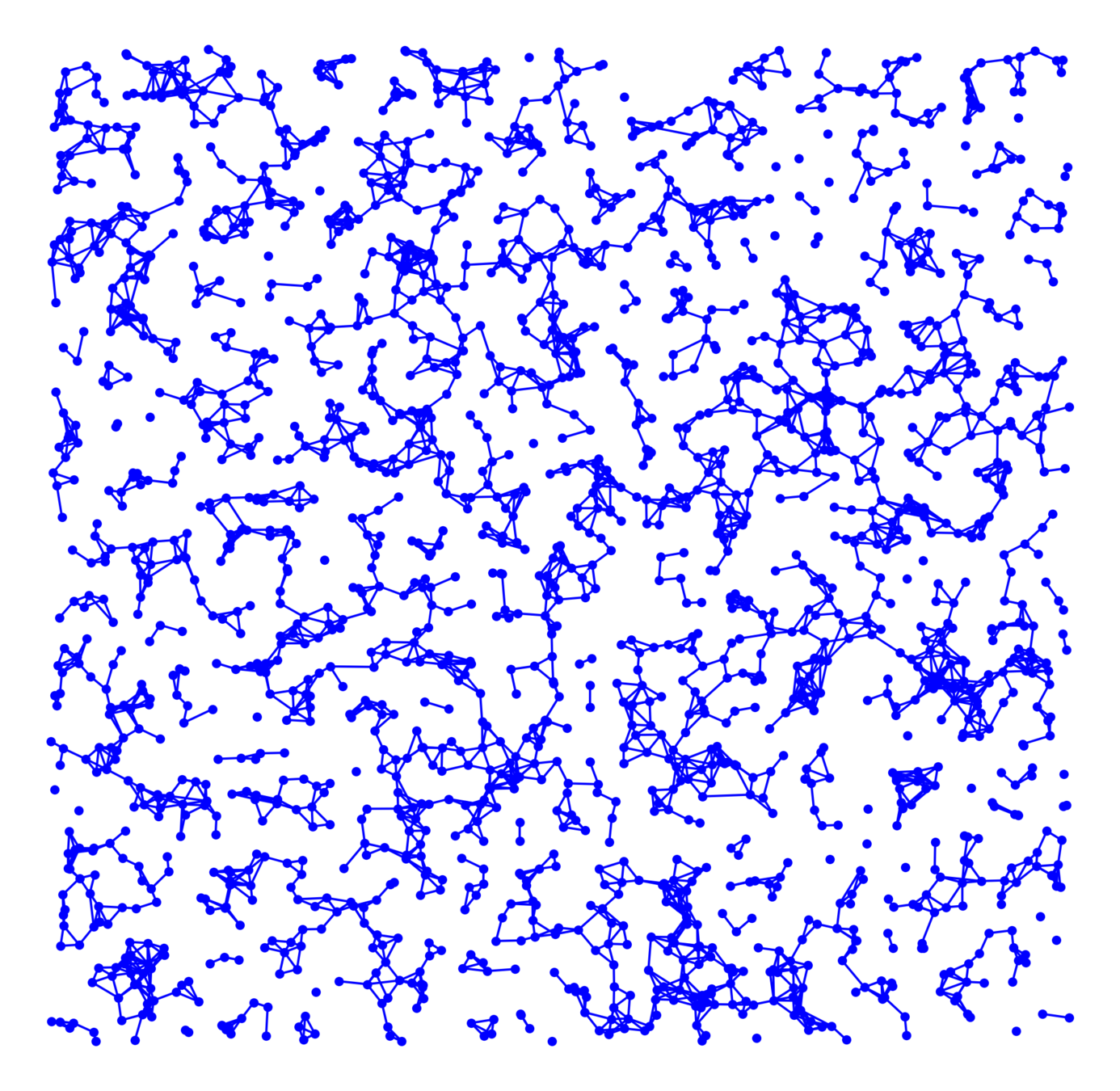
Long-range percolation

Random geom. graph

Nearest-neighbor percolation

Degree distribution

\frac{\sigma}{\tau-1}

\frac1{\tau-1}

1

\sigma=\tau-1

\tau=2

\sigma=1

\sigma=\tau-2

\sigma=0

\tau_\mathrm{deg}=\tau

\tau_\mathrm{deg}=\tfrac{\sigma+1}{\sigma-(\tau-2)}

\mathrm{deg}(0)=\infty

Theorem. When $\tau>2$:

Theorem. When $\tau<2$:

Infinite degrees
Bounded diameter

$$\mathbb{P}(\mathrm{deg}(0)\ge k)\sim k^{-(\tau_\mathrm{deg}-1)}.$$

[Deijfen, v.d. Hofstad, Hooghiemstra '13]

[Gracar, Grauer, Lüchtrath, Mörters '18]

[Heydenreich, Hulshof, Jorritsma '17]

[Hirsch '17]

[v.d. Hofstad, v.d. Hoorn, Maitra, '22]

[Jorritsma, K., Mitsche, '23]

[Lüchtrath '22]

Theorem. When $\tau<2$:

Theorem. When $\tau>2$:

$${\color{grey}\mathbb{P}(\mathrm{deg}(0)\ge k)\sim k^{-(\tau_\mathrm{deg}-1)}.}$$

Understanding network models

Probability, Combinatorics

& Physics, Epidemiology, ...

Information diffusion in random graphs

Distances

Component sizes

Intervention strategies

FINAL SIZE

Randomized optimization algorithms

Optimization under chance constraints

Sampling algorithms for explainable AI

Inhomogeneous degrees, triangles, and small world

Inhomogeneous degrees, triangles, and small world

Inhomogeneous degrees, triangles, and small world

Inhomogeneous degrees, triangles, and small world

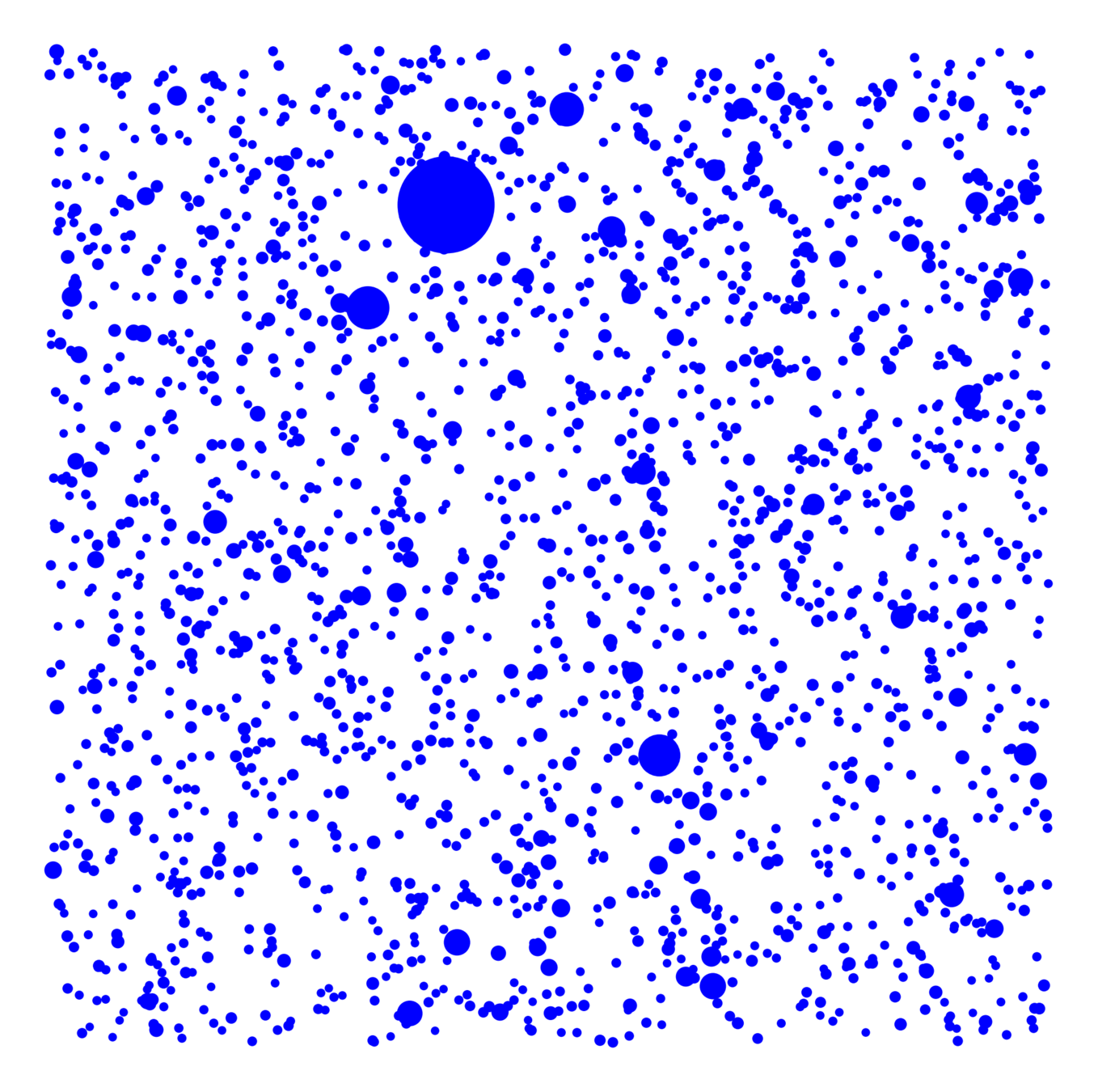
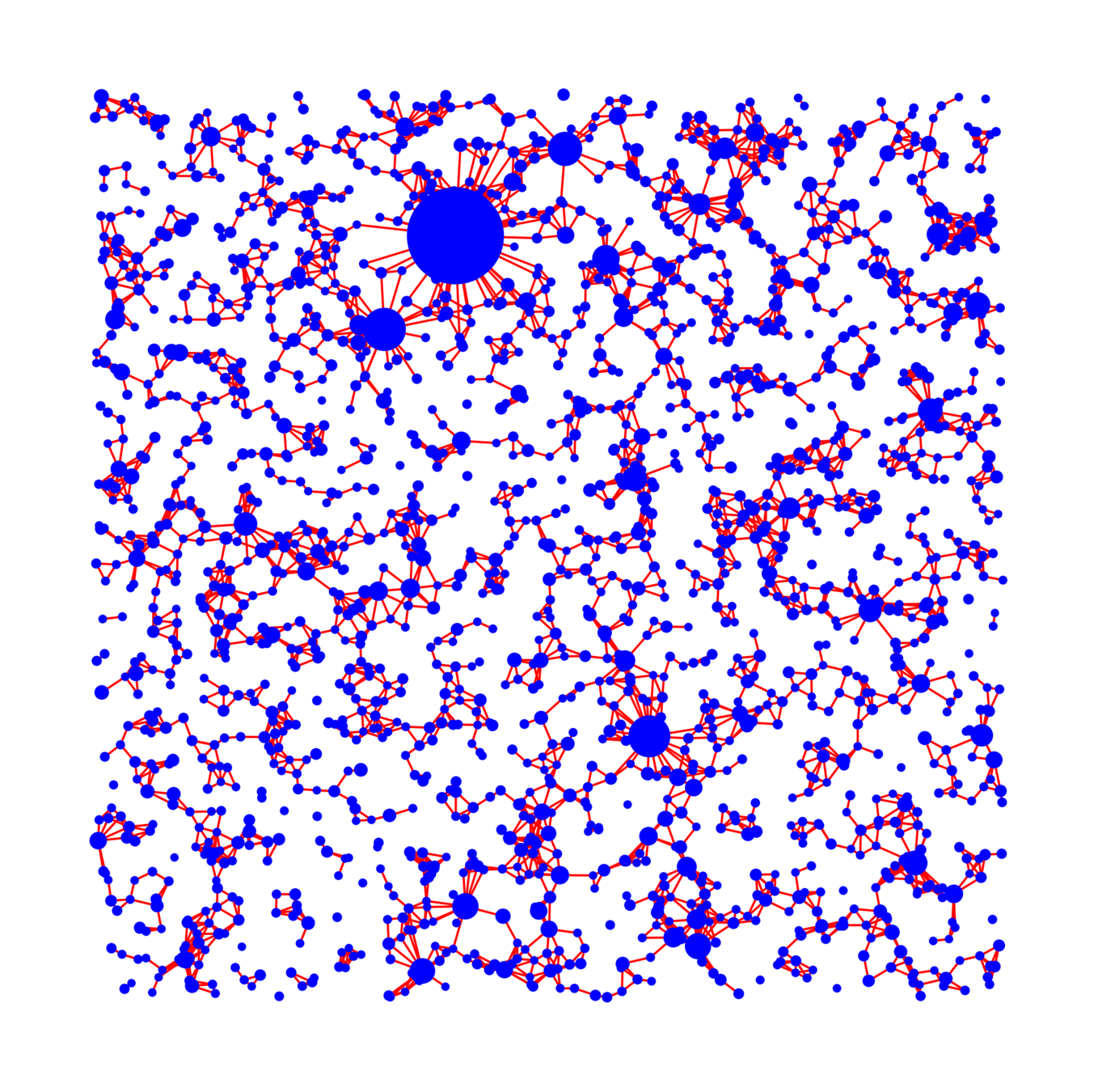
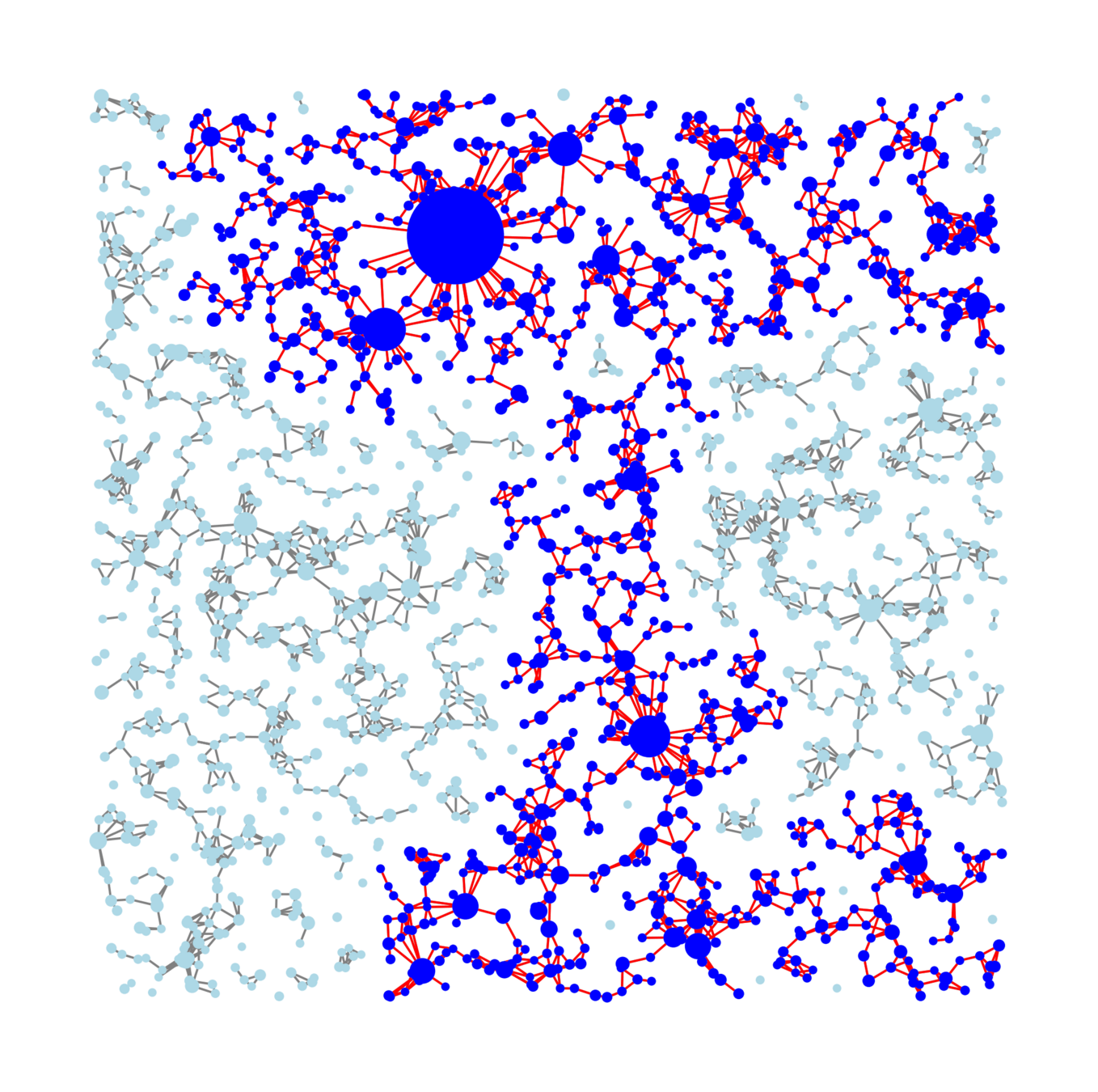
Vertex set

Spatial locations
Vertex weights

Edge more likely if

Spatially nearby,
High weight

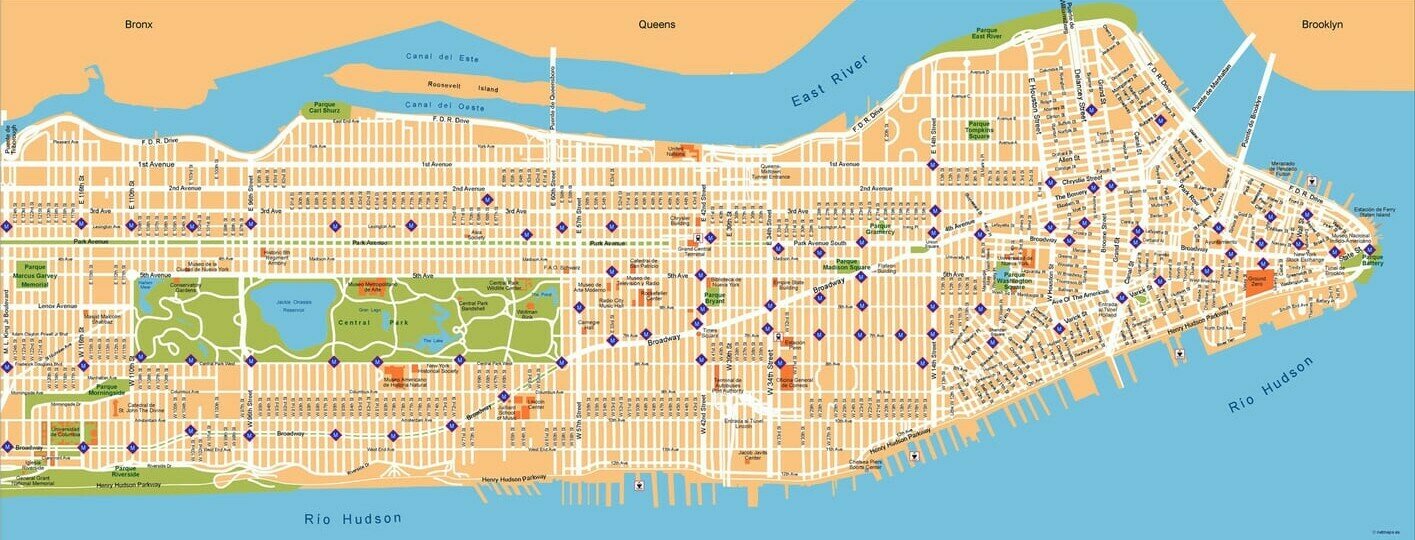
Spatial random graphs

Percolation: Reed-Frost epidemic

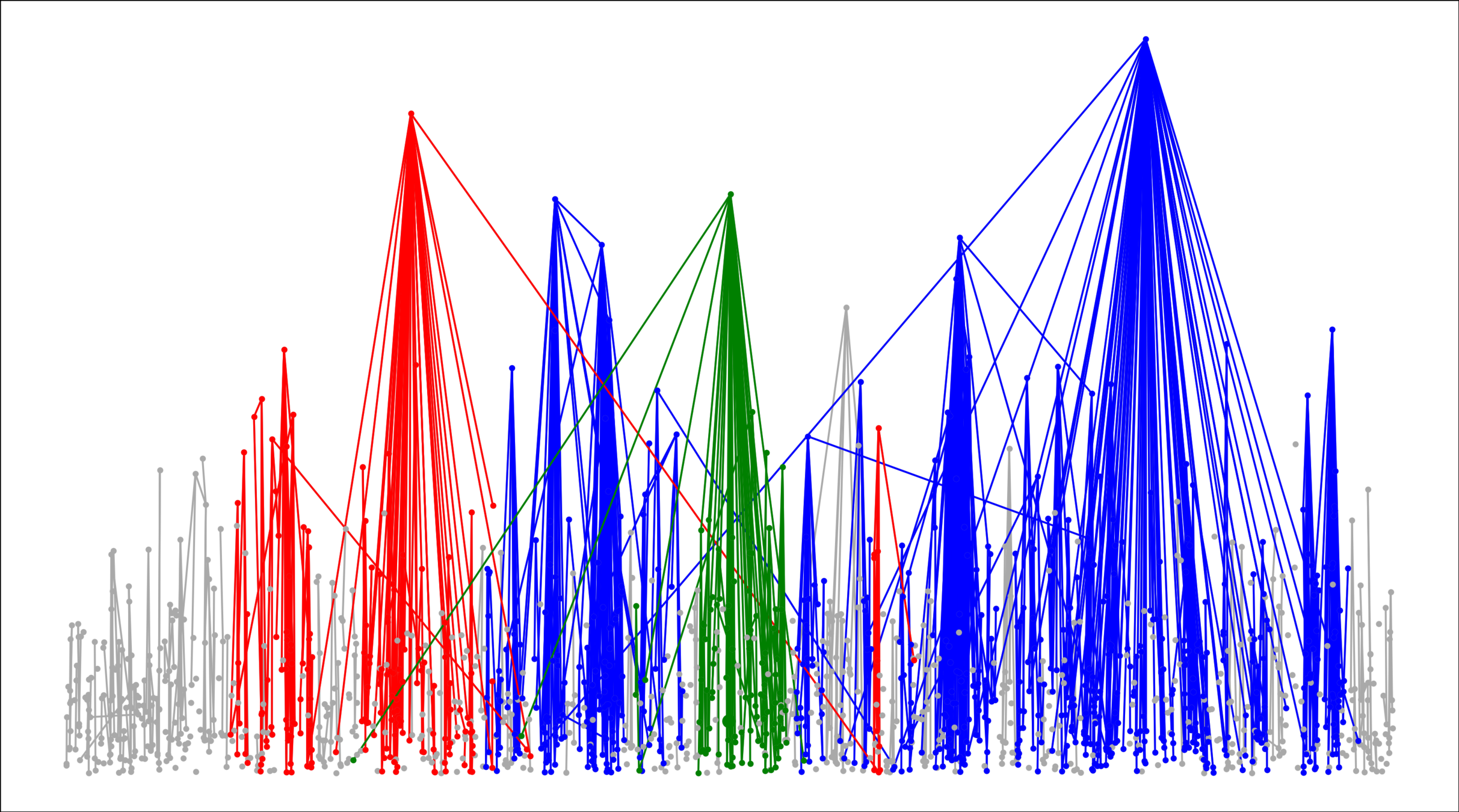
Four parameters: new and classical models

New phenomena

Delocalized connected components
Double-exponential neighbourhood growth
Large outbreaks more likely than small outbreaks

Challenges

Geometry:
- Short/Long edges
Presence of hubs

References

The Continuum Random Tree; David Aldous; Annals of Probability (1991).
Limits of multiplicative inhomogeneous random graphs and Lévy trees: limit theorems;
Nicolas Broutin, Thomas Duquesne, Minmin Wang; Probability Theory & Related Fields (2021).
Cluster-size decay in supercritical long-range percolation;
With Júlia Komjáthy, Dieter Mitsche; Electronic Journal of Probability (2024).
Cluster-size decay in supercritical kernel-based spatial random graphs;
With Júlia Komjáthy, Dieter Mitsche; Min. revision in Annals of Probability, arXiv: 2303.00712.
Large deviations of the giant in supercritical kernel-based spatial random graphs;
With Júlia Komjáthy, Dieter Mitsche; Preprint arXiv: 2404.02984.
Surface order large deviations for Ising, Potts and percolation models;
Agoston Pisztora; Probability Theory and Related Fields (2024).

Department Away Day `24

Joost Jorritsma

Random graph models for real-world networks

Department Away Day `24

Joost Jorritsma

Internet: a growing network of routers and servers

~1969: 2 connected sites

Time

~1989: 0.5 million users

~2023: billions of devices

[Faloutsos, Faloutsos & Faloutsos, '99]:
- Short average distance:
  Quick spread of information

~1999: 248 million users

Distance evolution in a growing network

1999

$\mathrm{dist}_{\color{red}{'99}}(u_{'99}, v_{'99}) = 4$

2005

$\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3$

2024

$\mathrm{dist}_{{\color{red}'24}}(u_{'99}, v_{'99}) = 2$

21 possible networks

Attachment rule:

Prefer connecting to high-degree vertices, $\tau$: tail of power-law degree distribution

2005

$\phantom{\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3}$

Distance evolution

Distance evolution: hydrodynamic limit

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume $\tau<3$.
Let $t'=T_t(a):=t\exp\big(\log^a(t)\big)$ for $a\in[0,1]$, then

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}\longrightarrow 0.$$

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume $\tau<3$.
Let $\phantom{t'=T_t(a):=t\exp\big(\log^a(t)\big)}$ for $\phantom{a\in[0,1]}$, then

$$ \phantom{\sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.}$$

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume $\tau<3$.
Let $t'=T_t(a):=t\exp\big(\log^a(t)\big)$ for $a\in[0,1]$, then

$$ \phantom{\sup_{a\in[0,1]}} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} \phantom{- (1-a)\frac{4}{|\log(\tau-2)|}}\right|\phantom{\overset{\mathbb{P}}\longrightarrow 0.}$$

```
Dynamics in PAMs.
```

Generalization with edge weights: 
random transmission times

Novelties

```
Fast spreading among influentials;
```

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume $\tau<3$.
Let $t'=T_t(a):=t\exp\big(\log^a(t)\big)$ for $a\in[0,1]$, then

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\phantom{\overset{\mathbb{P}}\longrightarrow 0.}$$

Theorem [J., Komjáthy, Annals of Applied Probability '22]. Assume $\tau<3$.
Let $t'=T_t(a):=t\exp\big(\log^a(t)\big)$ for $a\in[0,1]$, then

$$ \phantom{\sup_{a\in[0,1]}} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\phantom{\overset{\mathbb{P}}\longrightarrow 0.}$$

Information diffusion in random graphs

Distances

Component sizes

Intervention strategies

FINAL SIZE

Real networks contain many triangles!

Do real networks look like this?

Large deviations (rare events) of cluster sizes

Kernel-based spatial random graphs

Only four parameters

Vertex set

Spatial locations
Vertex weights

Edge more likely if

Spatially nearby,
High weight

Hyperbolic random graph

Scale-free percolation

Long-range percolation

Bond percolation on $\mathbb{Z}^d$

\exp\big(-\Theta(\sqrt{n})\big).

Theorem ($\mathbb{Z}^d$-like graphs)

[Lebowitz & Schonmann '88; Gandolfi '89; Grimmett, Marstrand '90;

Kesten, Zhang '90; Alexander, Chayes, Chayes, Newman '90; Pisztora '96;
Cerf '97; Contreras, Martineau, Tassion '2024; ...]

Lower tail:
Surface tension drives too small cluster

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n< \theta-\varepsilon\big)=

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta +\varepsilon\big)= \phantom{\Theta\big(n^{-I(\varepsilon)}\big)}

Upper tail:
Large clusters are very unlikely

\exp(-\Theta(n)\big).

Figure by Tobias Muller

Hyperbolic random graph

Scale-free percolation

Long-range percolation

Bond percolation on $\mathbb{Z}^d$

\exp\big(-\Theta(\sqrt{n})\big).

Theorem ($\mathbb{Z}^d$-like graphs)

[Lebowitz & Schonmann '88; Gandolfi '89; Grimmett, Marstrand '90;

Kesten, Zhang '90; Alexander, Chayes, Chayes, Newman '90; Pisztora '96;
Cerf '97; Contreras, Martineau, Tassion '2024; ...]

Lower tail:
Surface tension drives too small cluster

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n< \theta-\varepsilon\big)=

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta +\varepsilon\big)= \phantom{\Theta\big(n^{-I(\varepsilon)}\big)}

Upper tail:
Large clusters are very unlikely

\exp(-\Theta(n)\big).

Question:

Long edges and high-degree vertices,

do they matter?

\exp\big(-\Theta(n^\zeta)\big).

Theorem [J., Komjáthy, Mitsche, '24+]
We find explicit $\zeta\in[1/2,1)$, $\theta\in(0,1)$ s.t.

Lower tail: small final size
If enough long edges or no hubs

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n< \theta-\varepsilon\big)=

Novelties

Reversed discrepancy: large outbreak likelier than small.

Long edges can beat surface tension: any         ;

\zeta\!\in\![1/2, 1)

  governs second-largest cluster, and cluster of 0

\zeta

Techniques: probability, combinatorics, optimization.

What is the influence of long edges and high-degree vertices?

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>\theta +\varepsilon\big)= \phantom{\Theta\big(n^{-I(\varepsilon)}\big)}

Upper tail: large final size
If hubs are present, we find rate funtion $I(\varepsilon)$:

What is the influence of long edges and high-degree vertices?

\Theta\big(n^{-I(\varepsilon)}\big).

Information diffusion in random graphs

Distances

Component sizes

Intervention strategies

FINAL SIZE

Research plan: Large deviations in percolation and random graphs

Ongoing

Near future

Opportunities Leiden

Large deviations of the giant in inhomogeneous random graphs
Bert Zwart (CWI)
Tall or small trees
Serte Donderwinkel (Groningen)

Applying for CIRM Fellowship
Luisa Andreis (Milan),
MSc Students (Oxford)

Dalia Terhesu

Research plan: Random walks on random graphs

Ongoing

Opportunities Leiden

Random friend of a friend tree
Sofiya Burova (PhD student Barcelona),
Dieter Mitsche (Santiago de Chile)
Cover time of long-range percolation Carlos (MSc student Lima), D. Mitsche

(Evolution of) the mixing time of preferential attachment models (PAM)
Generating PAMs via random walks
Rajat Hazra & PhD student

Building a network: Attend and organize workshops, seminars

Near future (invitations)

One-world probability seminar
Probability meets Combinatorics (IST, Vienna)
Long-range phenomena in Percolation (Köln)
Mathematical Foundations of Network Models and their Applications (Chennai)

Opportunities Leiden: Lorentz Center

Organisational experience:
RandNET Workshop (with Serte Donderwinkel)

10 days, 80 participants
Mini-courses, Open problem sessions (4+ papers)
Budget: €55k
Attending prof:
"You set the gold standard for running such an event"

Spatial random graphs with tunable assortativity

Joost Jorritsma

Intriguing maths: classical network models

Intriguing maths: classical network models

Intriguing maths: classical network models

Intriguing maths: classical network models

Kernel-based spatial random graphs

The interpolating kernel

Degree distribution

Understanding network models

Probability, Combinatorics

& Physics, Epidemiology, ...

Information diffusion in random graphs

Distances

Component sizes

Intervention strategies

Inhomogeneous degrees, triangles, and small world

Inhomogeneous degrees, triangles, and small world

Inhomogeneous degrees, triangles, and small world

Inhomogeneous degrees, triangles, and small world

Spatial random graphs

Four parameters: new and classical models

New direction: Scaling limits of trees and random graphs

References

Joost Jorritsma

Random graph models for real-world networks

Joost Jorritsma

Internet: a growing network of routers and servers

Distance evolution in a growing network

Distance evolution

Distance evolution: hydrodynamic limit

Information diffusion in random graphs

Distances

Component sizes

Intervention strategies

Real networks contain many triangles!

Do real networks look like this?

Kernel-based spatial random graphs

What is the influence of long edges and high-degree vertices?

What is the influence of long edges and high-degree vertices?

Information diffusion in random graphs

Distances

Component sizes

Intervention strategies

Research plan: Large deviations in percolation and random graphs

Research plan: Random walks on random graphs

Building a network: Attend and organize workshops, seminars