Naresh Kumar Devulapally
CSE 4/573 Computer Vision
Apr 29, 2025
Convolutional Neural Networks
Naresh Kumar Devulapally

CSE 4/573: Computer Vision and Image Processing
naresh-ub.github.io
code at:
Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Convolutional Neural Networks
Apr 29, 2025
What are
Image Filters?
Features help
Neural Networks
Can we LEARN Image filters?
Convolutional
Neural Networks
Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Convolutional Neural Networks
Apr 29, 2025
Why
What are Neural Networks?
Convolution?
Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
Convolution
Recap


Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
Different Filters = different Transformations



Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
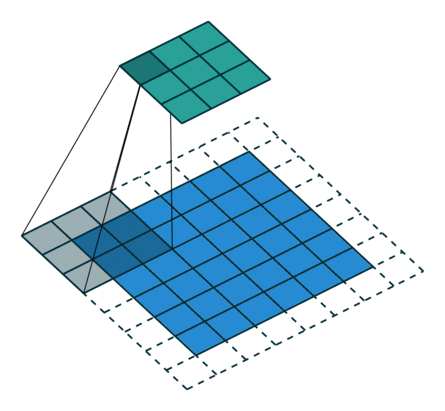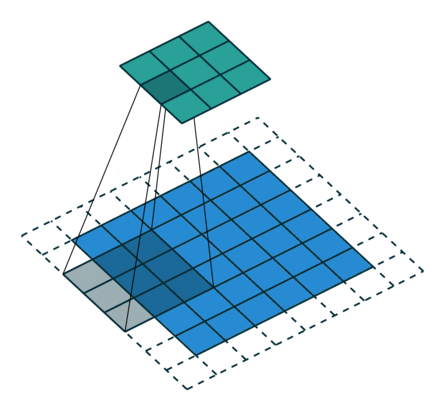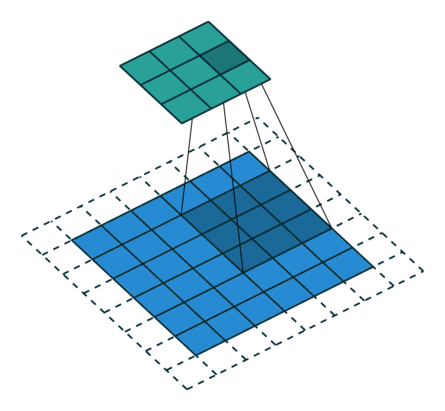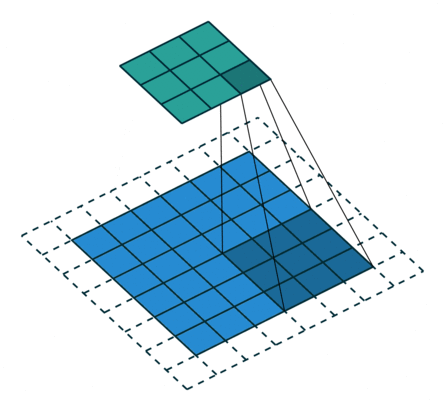
Parameters during Convolution


Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
Parameters during Convolution



Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
From Images to Classification Problem
Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
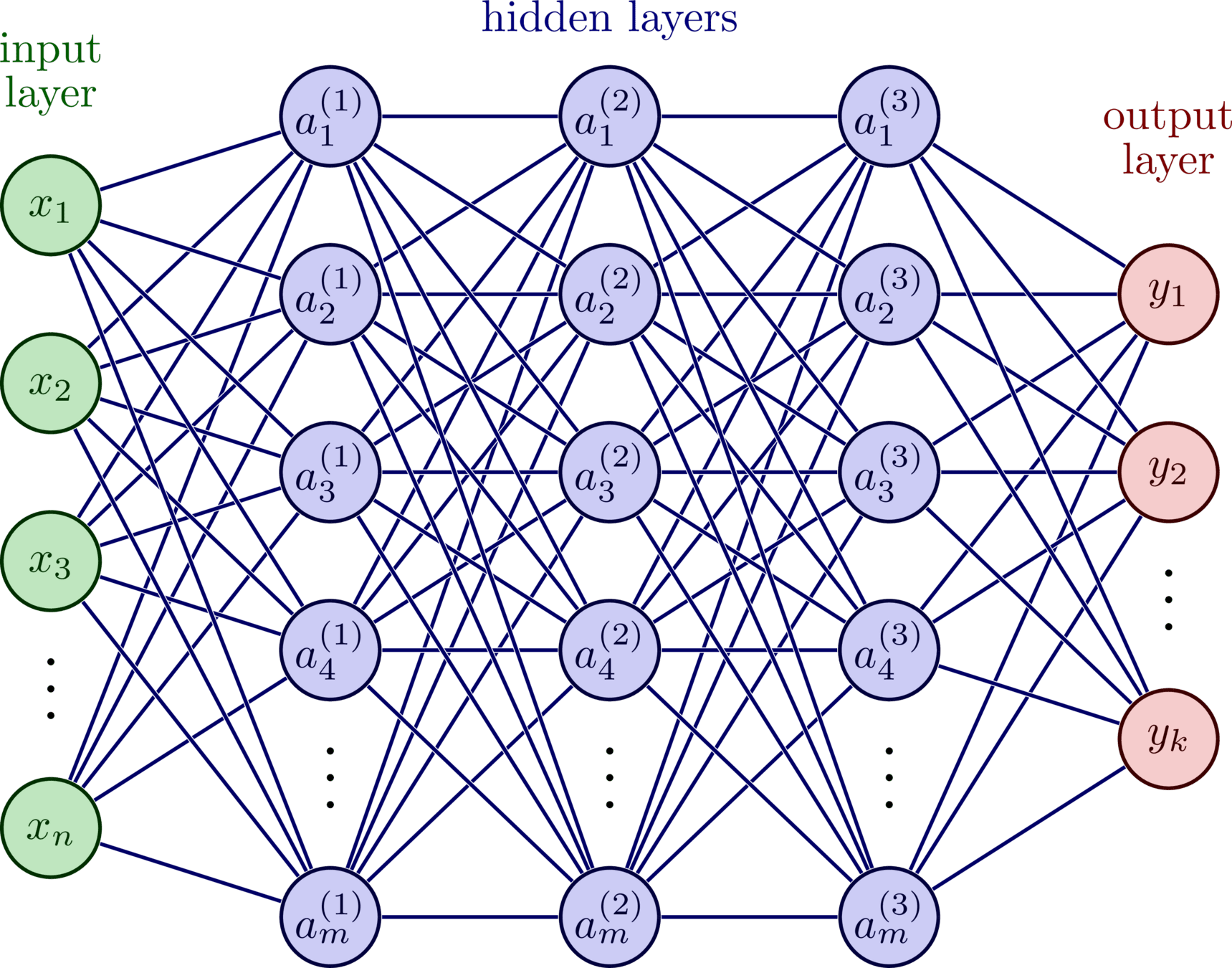
Neural Networks

Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
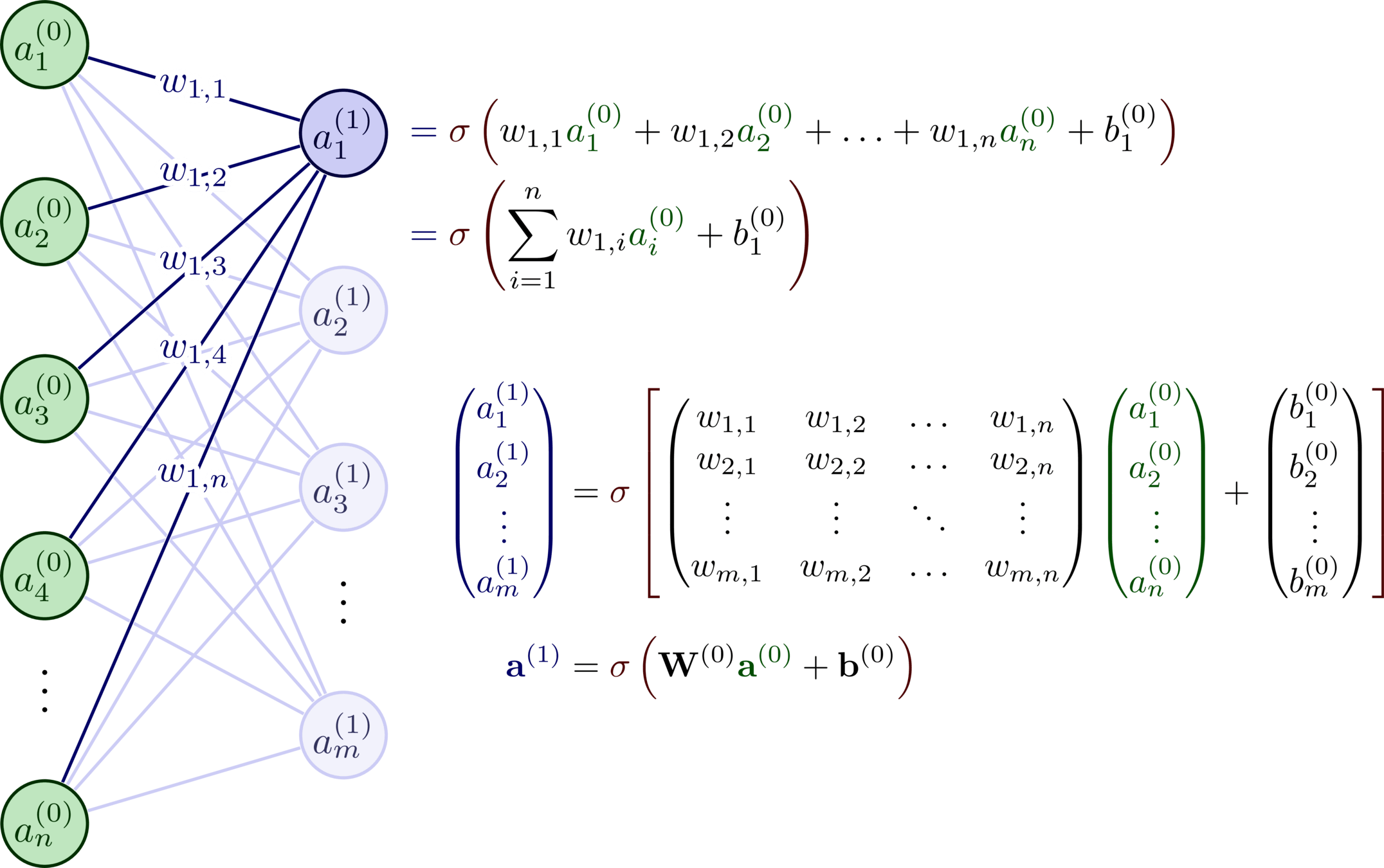
Neural Networks

Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
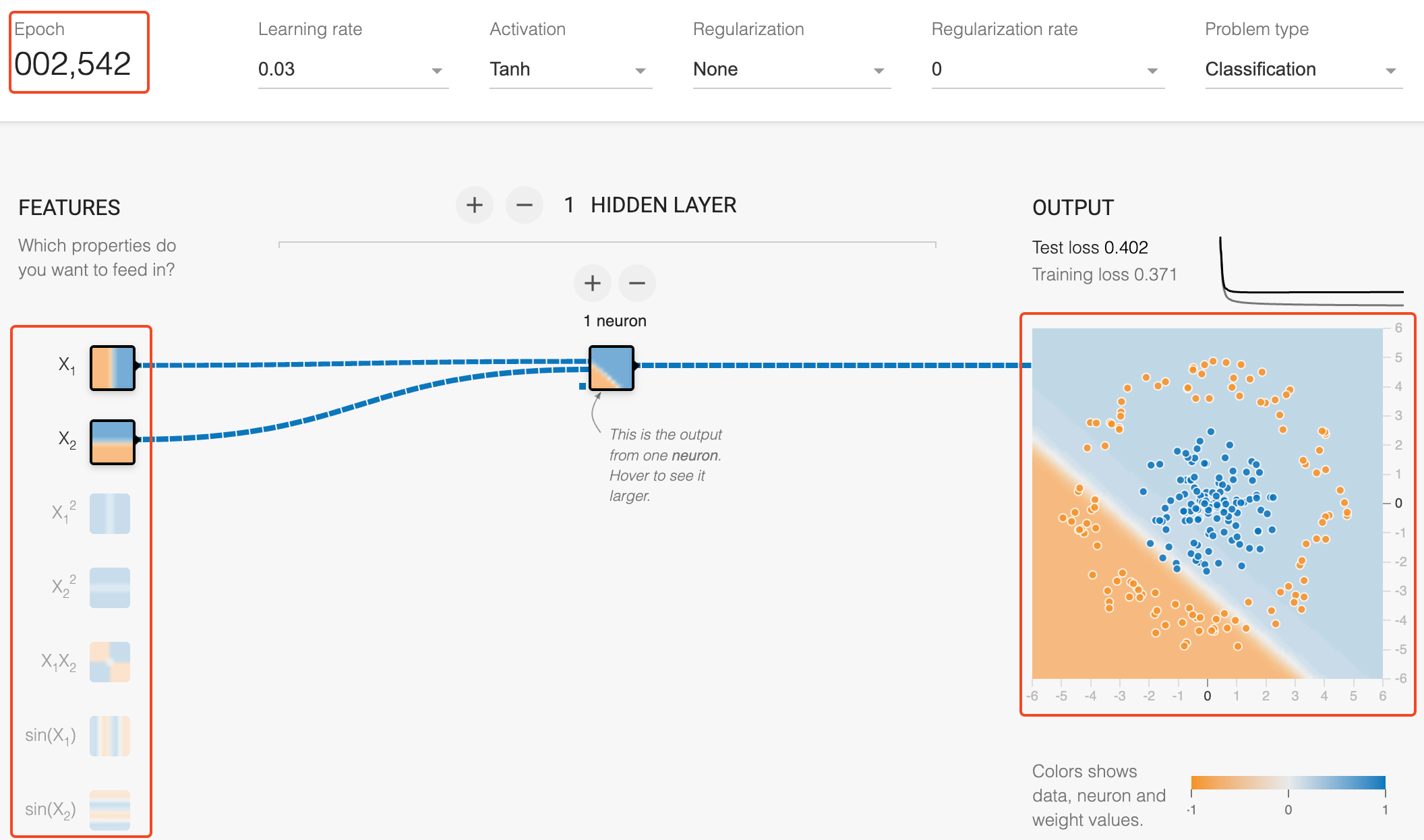
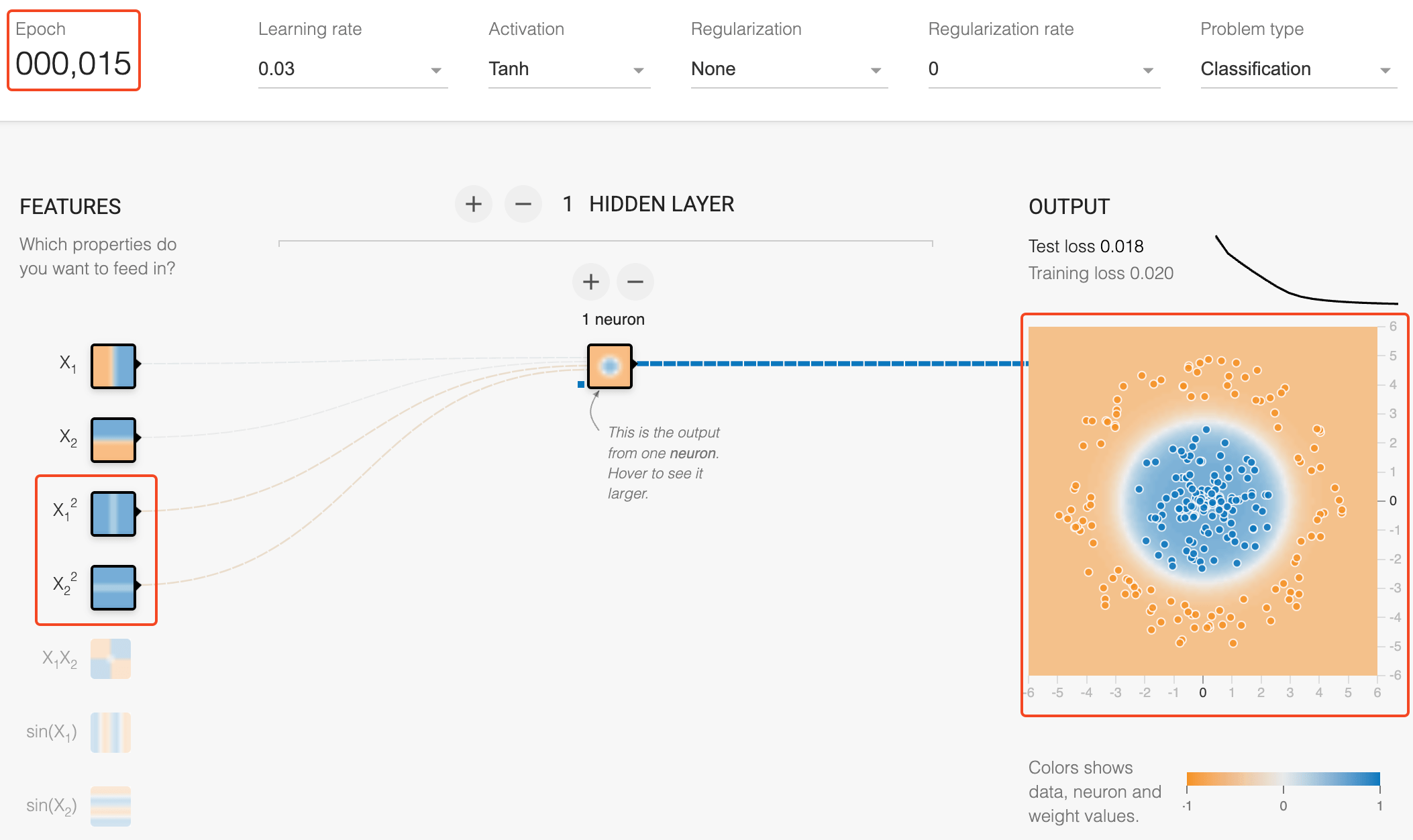
Neural Networks - Importance of Features
Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
Neural Networks - Importance of Features


Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
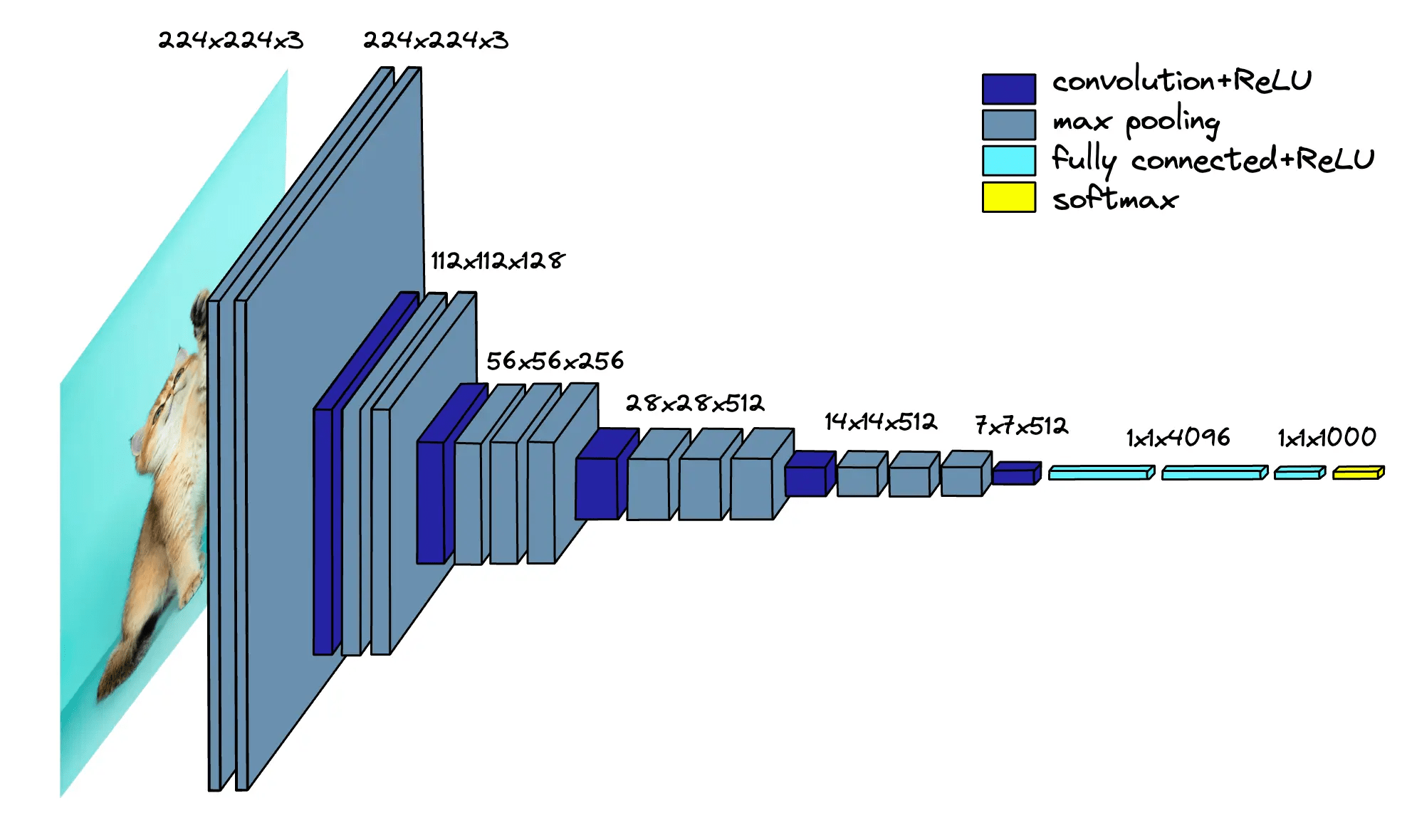
Convolutional Neural Networks
Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
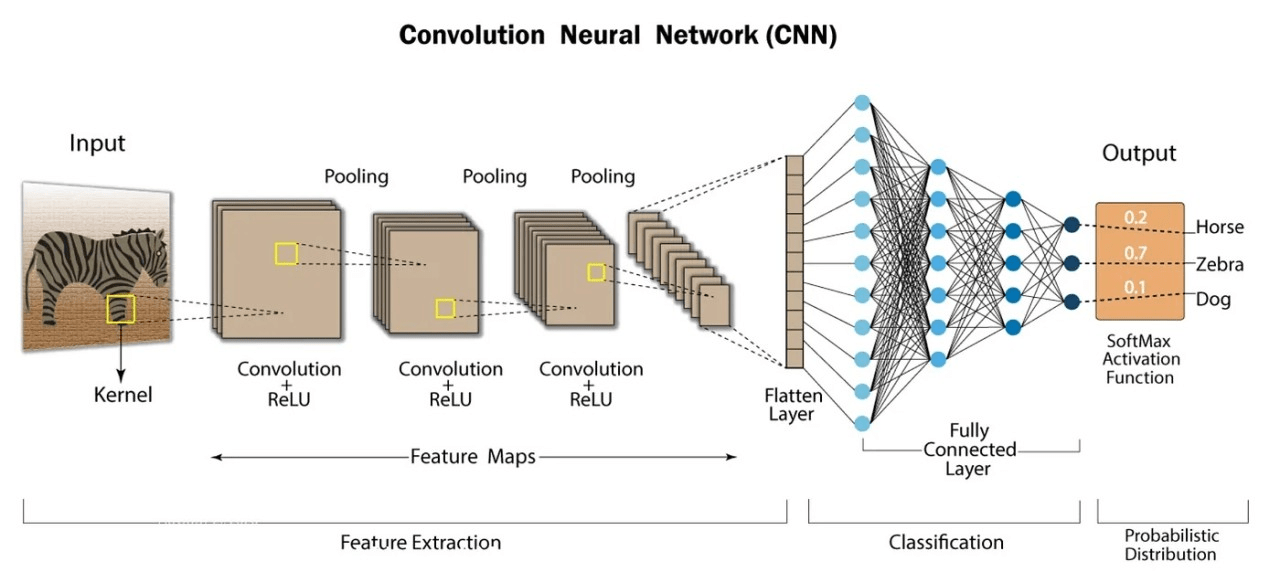
Convolutional Neural Networks
After convolution, the feature maps still contain a lot of redundant information, including slight variations or small shifts.
Max pooling helps by:
- Keeping only the strongest activations (important features)
- Making the network more robust to small translations or distortions
- Reducing the spatial size of the feature maps, thus reducing computation and parameters.
Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Apr 29, 2025
Convolutional Neural Networks