\text{Learning-based Computer Vision with Neural Networks}
\textbf{Naresh Kumar Devulapally}
\text{CSE 4/573: Computer Vision and Image Processing}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}
\text{July 1, 3 - 2025}
\text{Lectures 10, 11: July 1, 3 - 2025}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

- What is a function?
- Basics of Neural Networks (NNs) (Recap)
- Neural Networks for Classification
- Image Classification using Feedforward NNs
- Features help NNs
- Convolutional Neural Networks
- Important components of an NN pipeline
- Object Detection
- Semantic Segmentation
- Monocular Depth Estimation
- Midterm Recap (what to focus to score well)
\( \text{Agenda of this Lecture:}\)
\text{July 1, 3 - 2025}
\text{Learning-based Computer Vision with Neural Networks}
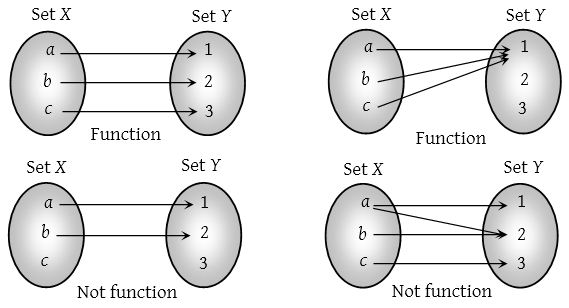
\text{What is a Function?}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}

y = f(x)
\text{What is a Function?}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
y = f(x)
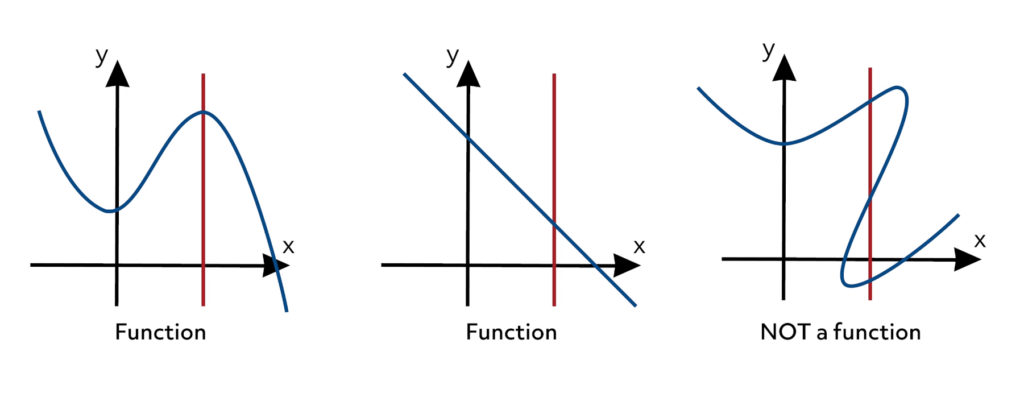
There are many ways to estimate a function \( y = f(x) \) based on data points. Discussion of such methods is outside the scope of this lecture.
In this lecture, we will discuss about powerful function approximators known as:
\text{Neural Networks}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Neural Networks}
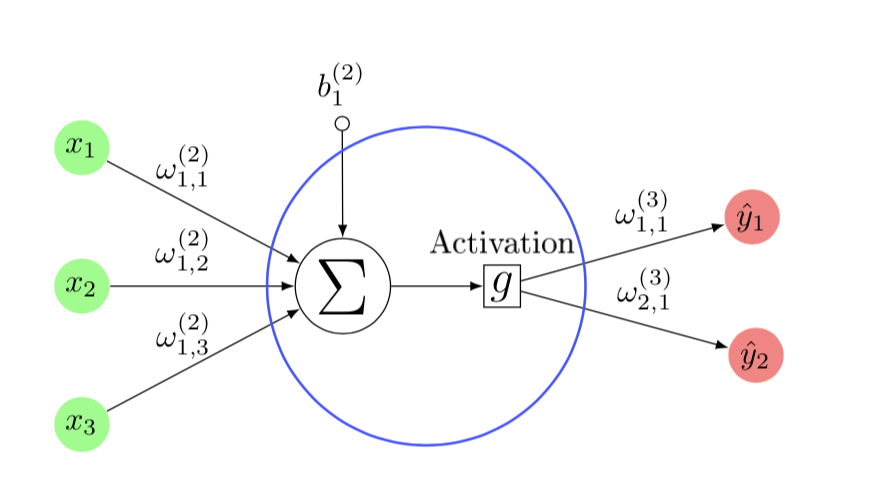
\hat{y}_j = \omega^{(3)}_{j,1} \cdot g \Big( \sum_{i=1}^{3} \omega^{(2)}_{1,i} x_i + b^{(2)}_{1} \Big),
\quad j = 1,2

\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Neural Networks}


\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Neural Networks}


\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Neural Networks}

\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Neural Networks}
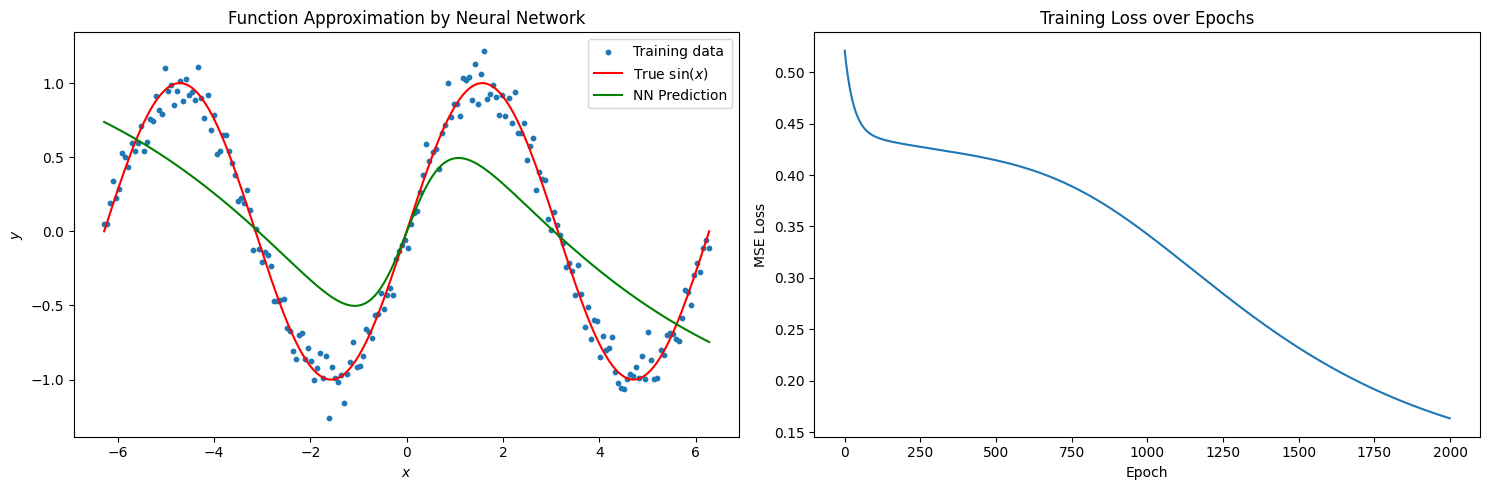
y = sin(x) + 0.1 * \mathcal{N}(0, 1)
Noise
NNs for function approximation (Regression)
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{NNs for Classification (Loss and Activation)}
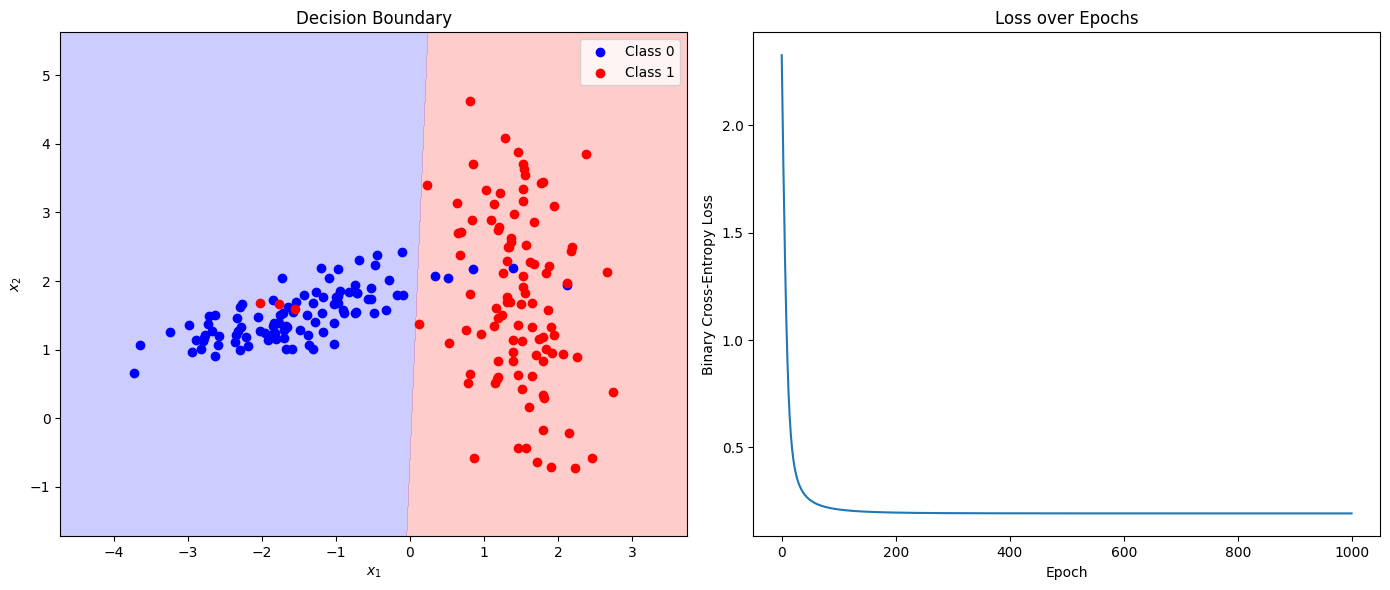
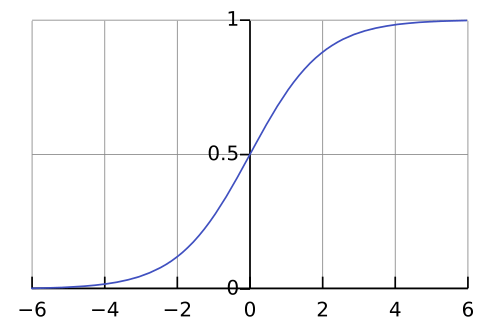
\hat{y} = \sigma(w_1 x_1 + w_2 x_2 + b)
Activation function
(Sigmoid for Binary Classfication)
\mathcal{L} = - \big[\, y \log(\hat{y}) + (1 - y) \log(1 - \hat{y}) \big]
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{NNs for Classification (Loss and Activation)}
Multi-class classification


\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{NNs for Classification (Loss and Activation)}
Takeaway: Loss and Activation change depending on the task at hand.
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{NNs for Classification (Larger Networks)}
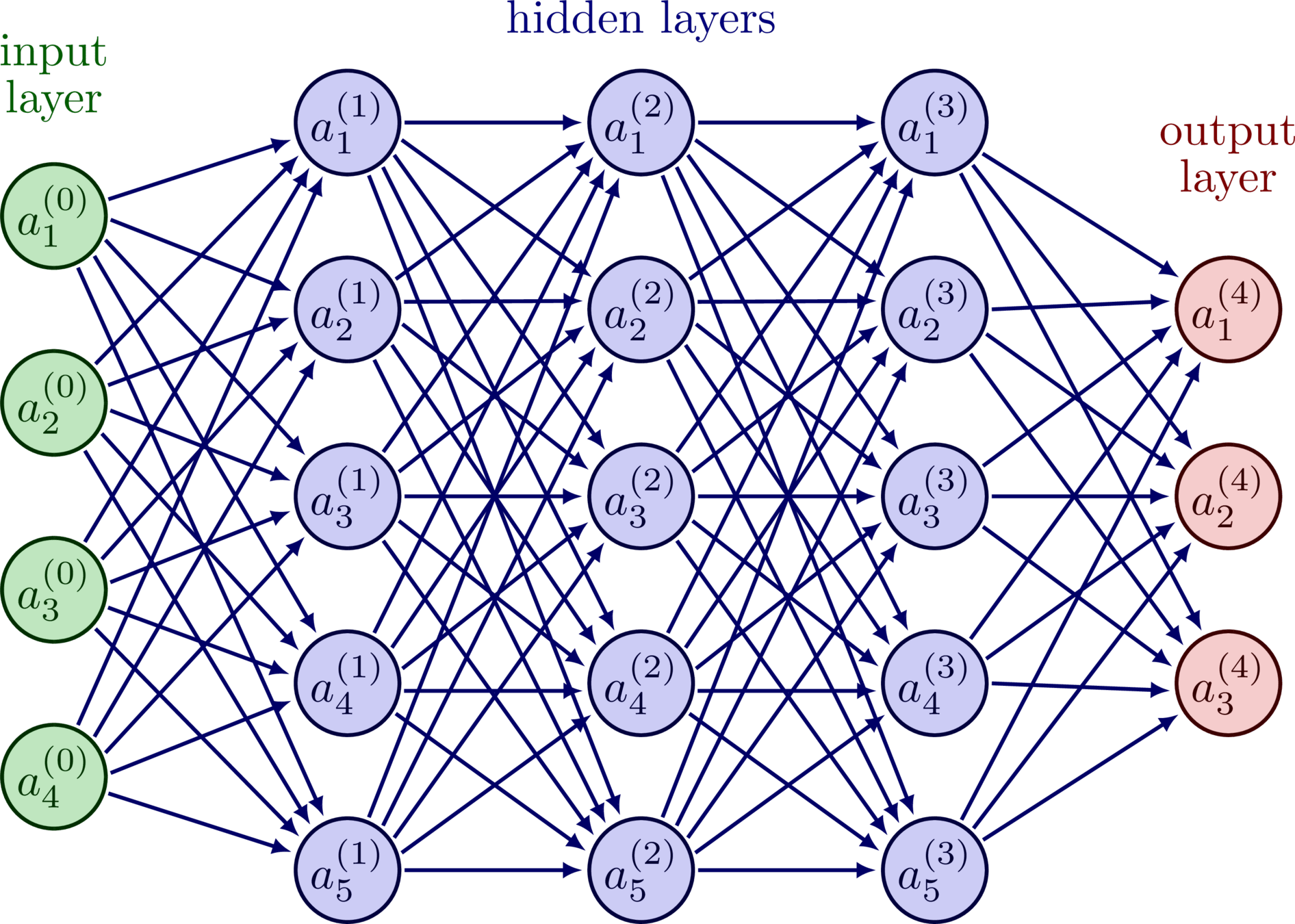
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
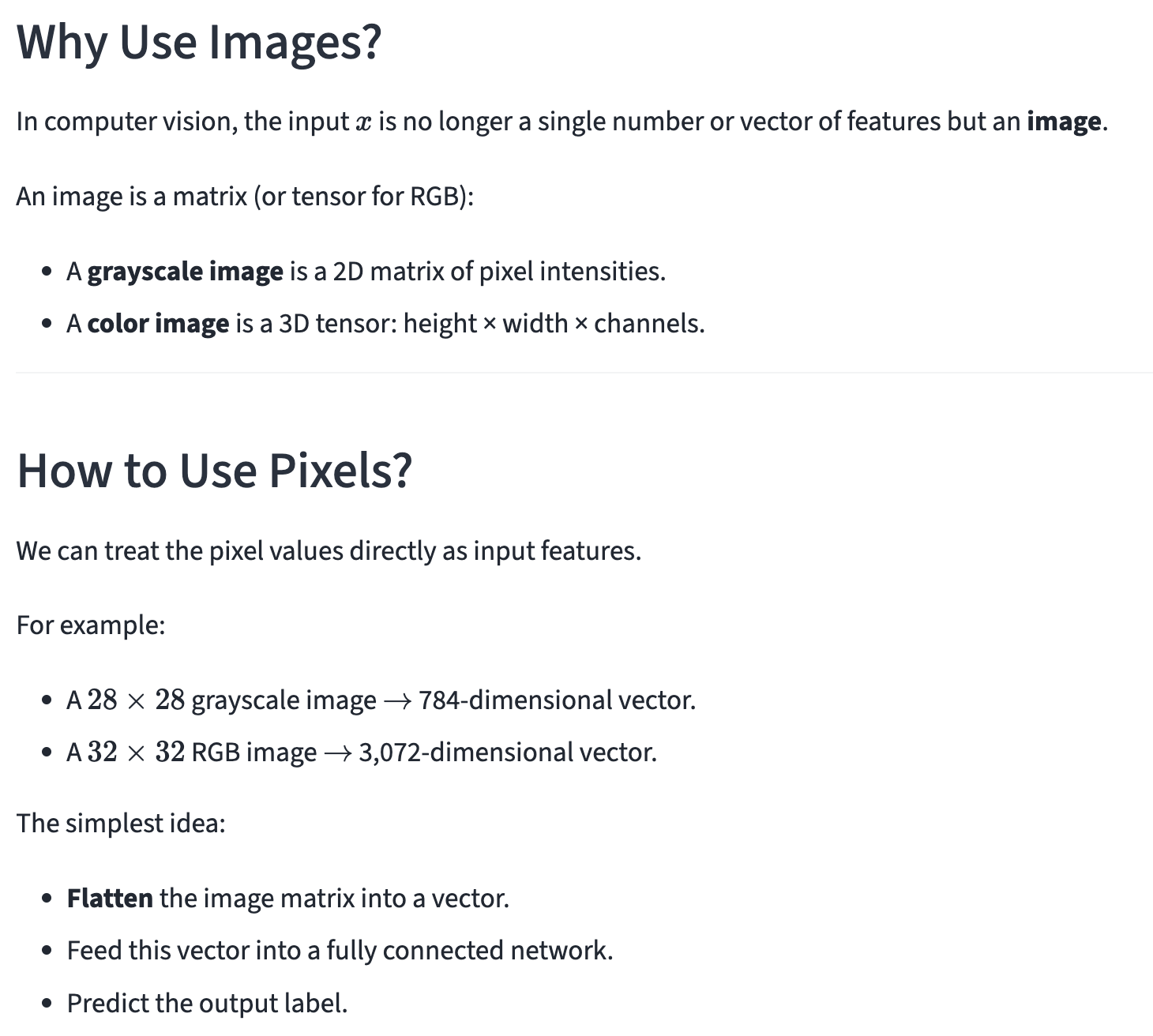
\text{NNs for Classification (Images)}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{NNs for Classification (Images)}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Features help Neural Networks}
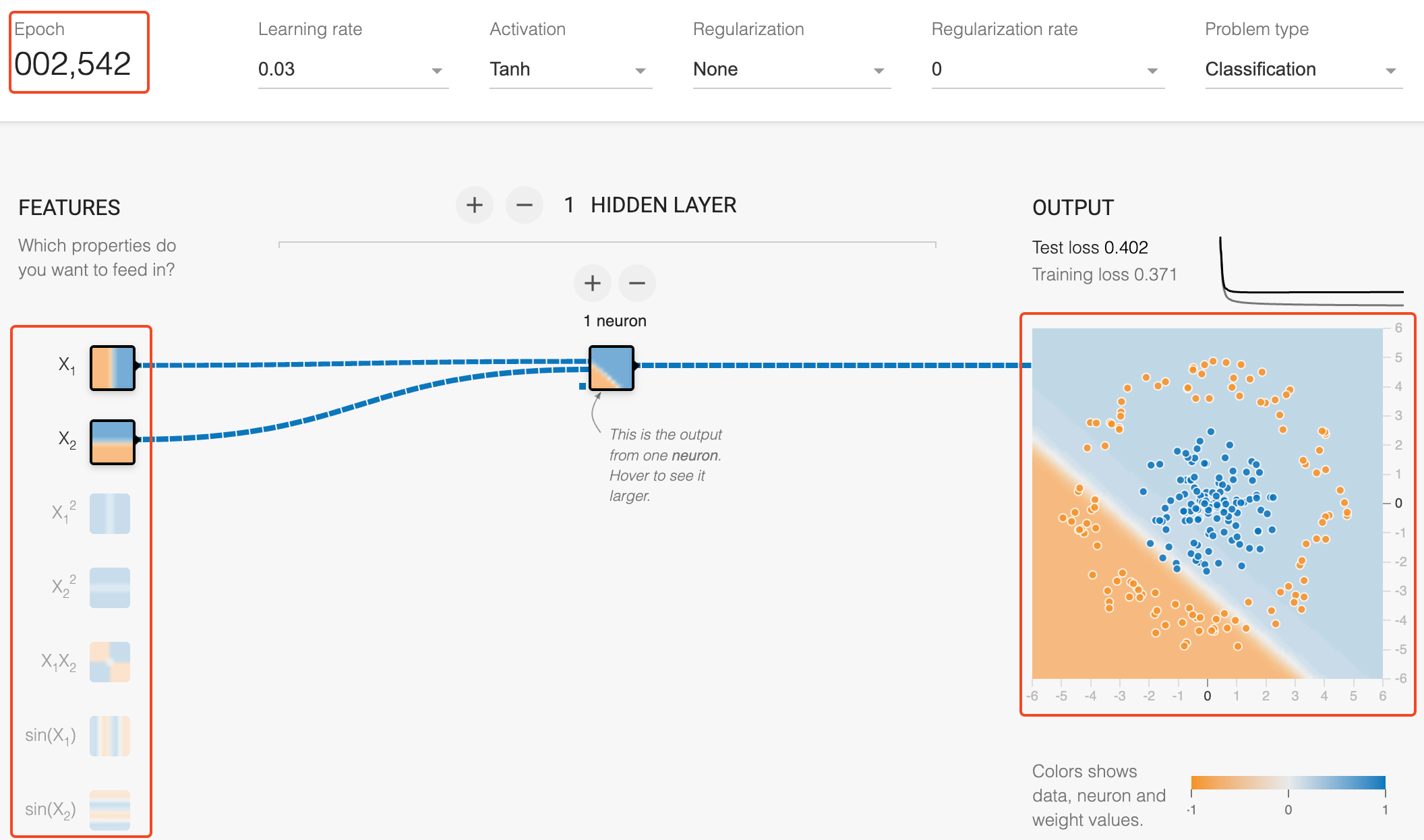
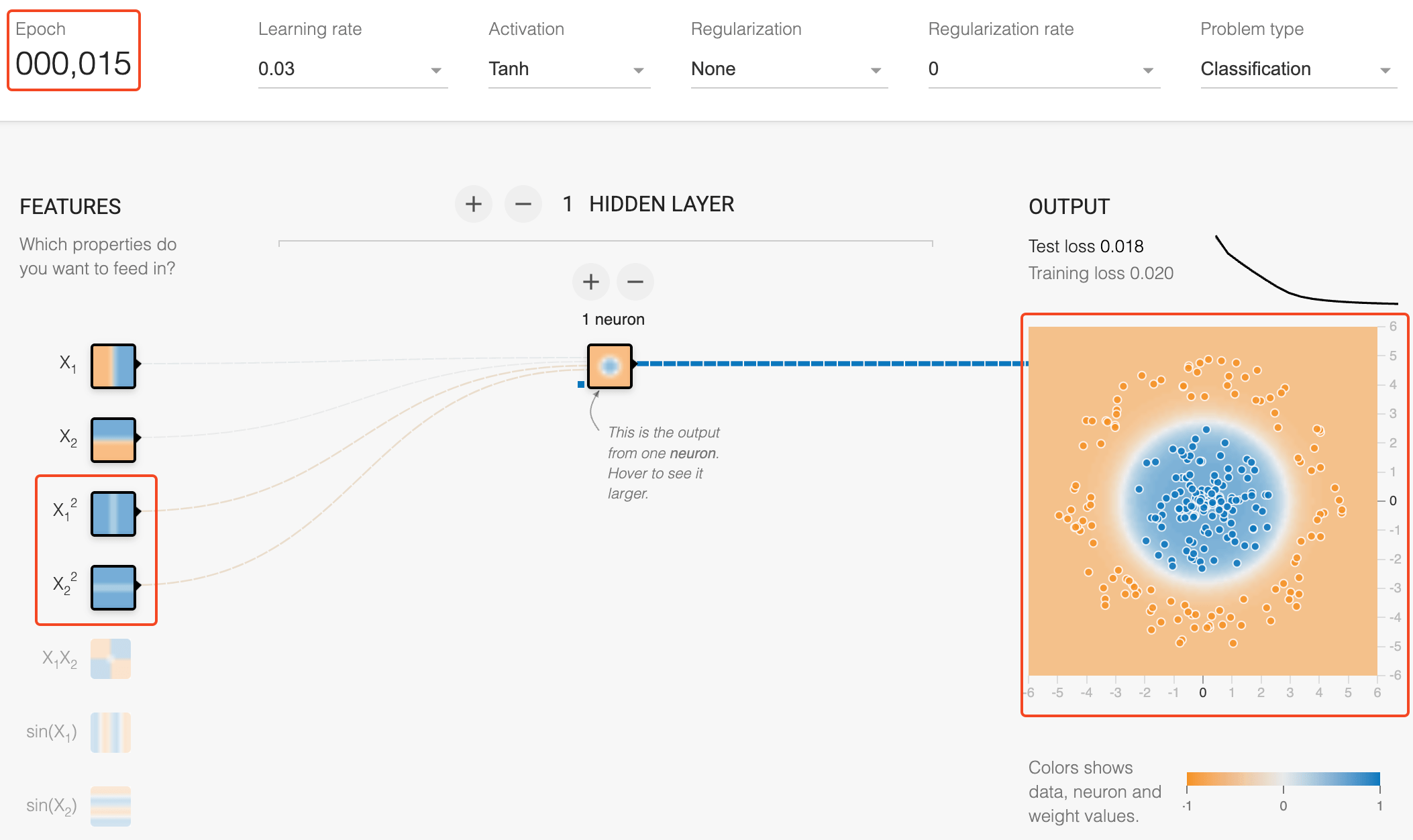
\text{Prediction without new features}
\text{Prediction WITH new features}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Features help Neural Networks}
What are those features in Images?
=
1
1
1
1
1
1
1
1
1
\frac{1}{9}
\times
-1
0
1
-2
-1
0
2
0
1
\frac{1}{9}
\times
=
-1
0
1
0
0
2
1
\frac{1}{9}
\times
\text{Blur}
\text{Vertical}
\text{Edges}
\text{Horizontal}
\text{Edges}
=


-1
-2

\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Features help Neural Networks}
What are those features in Images?
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
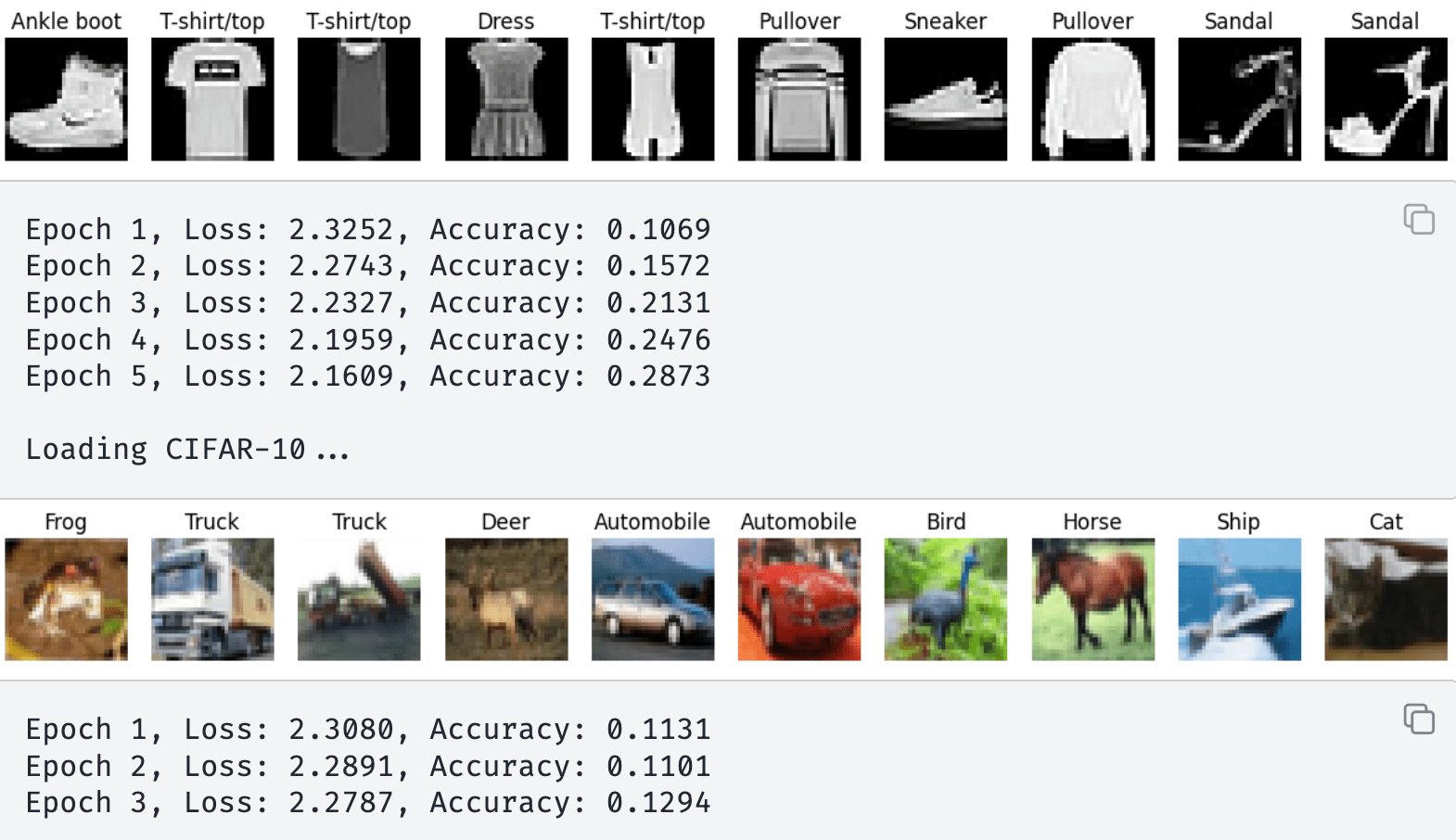
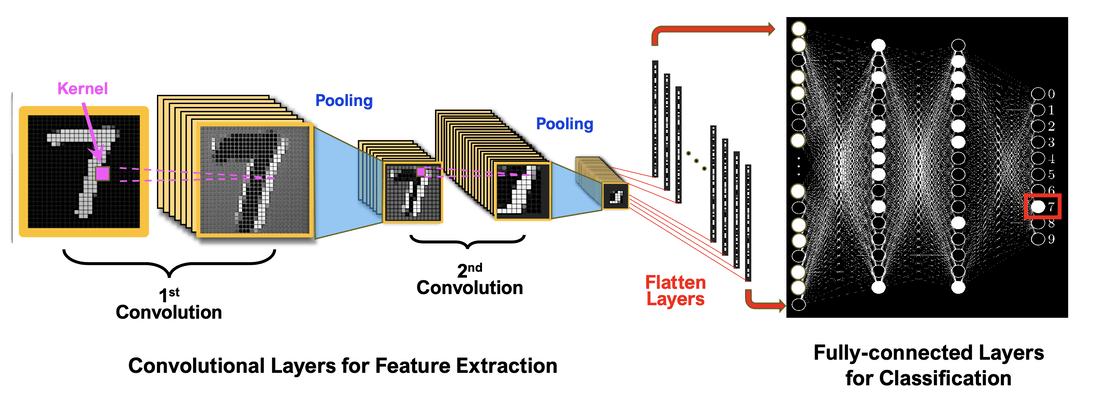
\text{Convolutional Neural Networks}
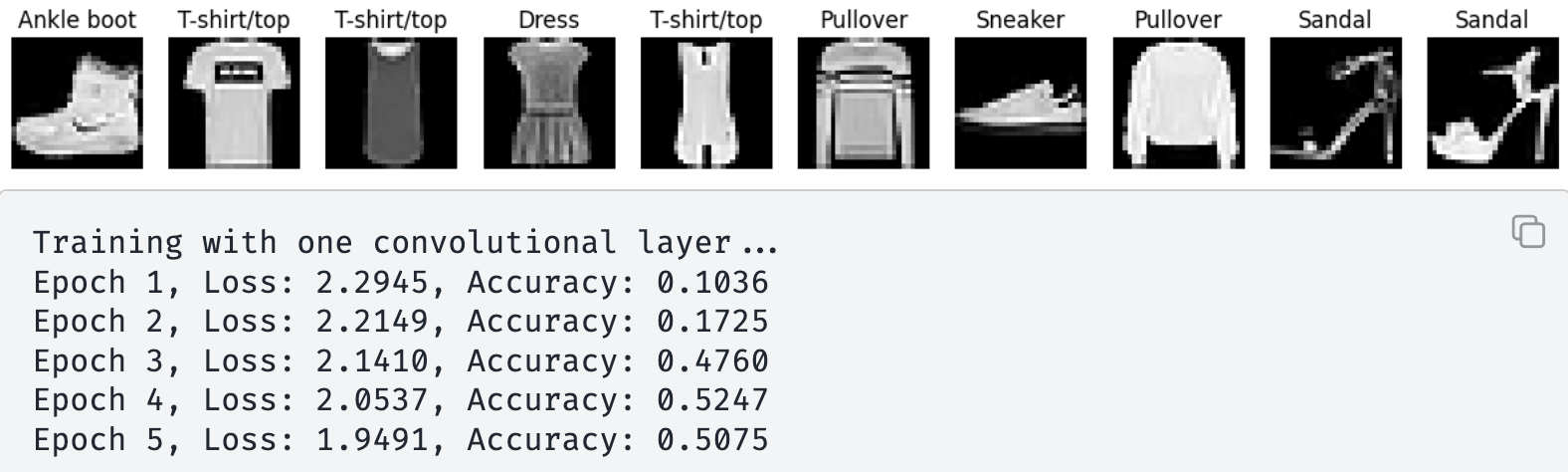

Feature Maps
was 0.2873 without Conv.
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Convolutional Neural Networks}
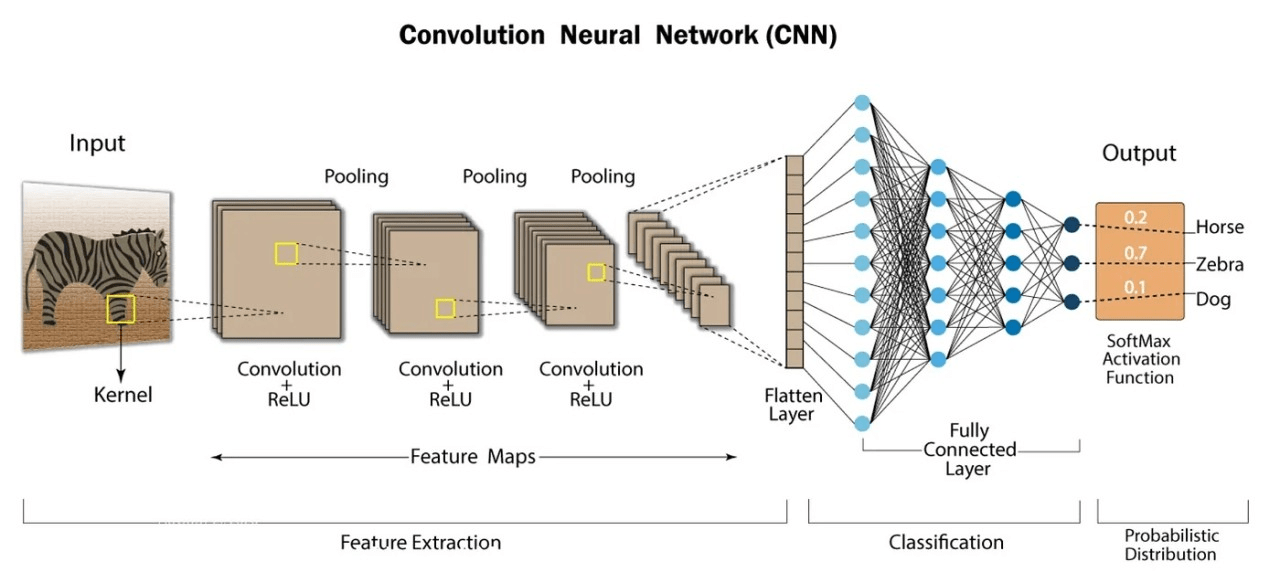
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Convolutional Neural Networks}
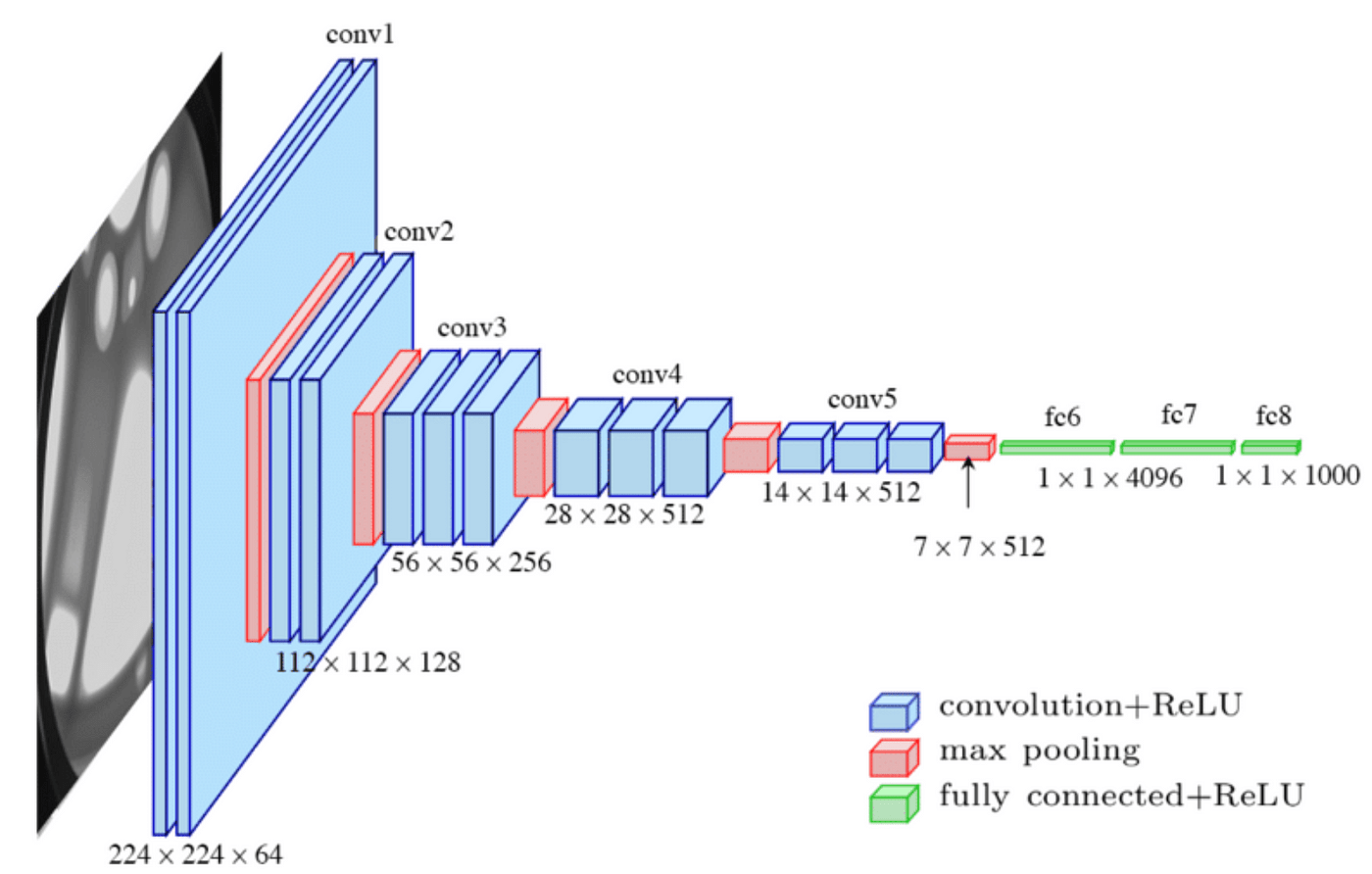
VGG (2014)
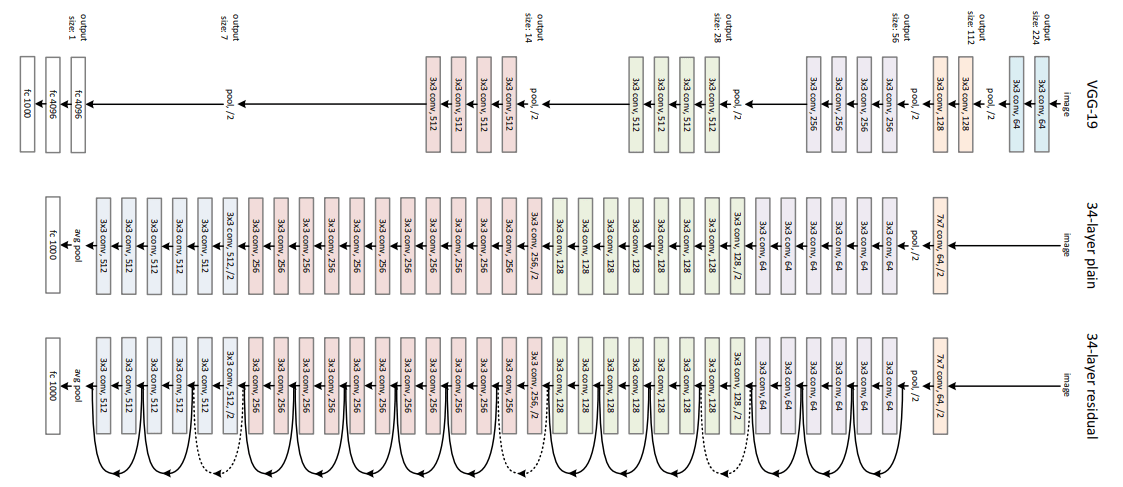
ResNet (2015)
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Convolutional Neural Networks}

\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Applications of NNs in CV: Object Detection}

\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Applications of NNs in CV: Object Detection}

Code available in Course Website
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Applications of NNs in CV: Segmentation}

\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Applications of NNs in CV: Segmentation}


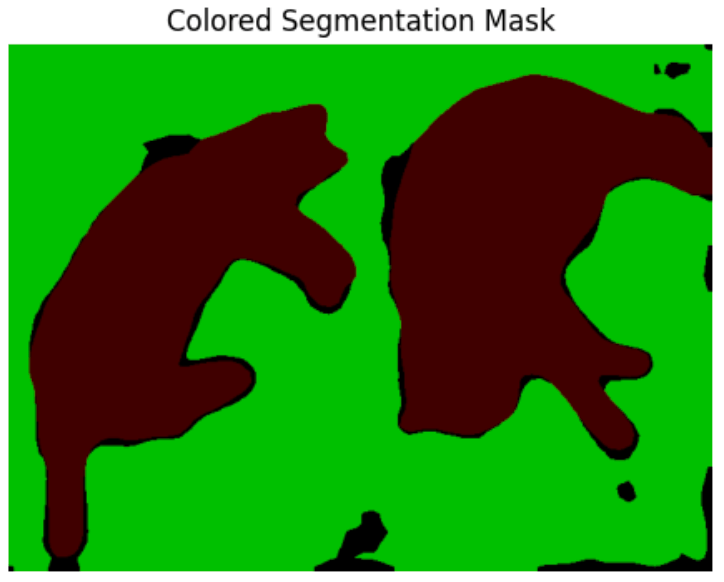
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Applications of NNs in CV: Depth Estimation}


\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Applications of NNs in CV: Depth Estimation}

\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Applications of NNs in CV: Many More}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Applications of NNs in CV: Many More}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Applications of NNs in CV: Many More}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{July 1, 3 - 2025}
\text{Applications of NNs in CV: Many More}