\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Latent Diffusion Unlearning: Protecting Against Unauthorized} \)

\( \text{ACM MM 2025} \)
\( \textbf{Personalization Through Trajectory Shifted Perturbations} \)



\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Latent Diffusion Unlearning: Protecting Against Unauthorized} \)

\( \text{ACM MM 2025} \)
\( \textbf{Personalization Through Trajectory Shifted Perturbations} \)
\( \text{Naresh Kumar Devulapally} \)
devulapa@buffalo.edu
\( \text{The State University of New York} \)
\( \text{at Buffalo} \)
\( \text{Shruti Agarwal} \)
shragarw@adobe.com
\( \text{Research Scientist} \)
\( \text{Adobe Research} \)
\( \text{Tejas Gokhale} \)
gokhale@umbc.edu
\( \text{University of Maryland} \)
\( \text{Baltimore County} \)
\( \text{Vishnu Suresh Lokhande} \)
vishnulo@buffalo.edu
\( \text{The State University of New York} \)
\( \text{at Buffalo} \)



\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Motivation} \)
\( \text{ACM MM 2025} \)
- Diffusion models (e.g., Stable Diffusion) can adapt to new subjects or styles with just a few images. Textual Inversion and DreamBooth achieve high-fidelity personalization rapidly.
Power of Personalization
Risks and Concerns
-
Privacy: Risk of misuse of private or identity-sensitive data.
-
Intellectual Property: Unauthorized style or content cloning.
-
Security: Uncontrolled replication of copyrighted material
\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Motivation} \)
\( \text{ACM MM 2025} \)
- Pixel-space perturbations make samples unlearnable. However...
- Visibly degrade quality (noise/artifacts).
- Vulnerable to purification defenses (e.g., DiffPure).
Limitations of Existing Defenses
Our Proposal
- Shift perturbations into latent space, altering the diffusion trajectory.
- Ensure perturbations are imperceptible yet robust to personalization and purification.
- Practical and scalable defense for safeguarding sensitive data.
\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Problem Statement} \)
\( \text{ACM MM 2025} \)
Approach: Introduce adversarial noise perturbations to ensure that certain images become unlearnable.
Goal: Prevent a diffusion model from learning and reproducing specific images while maintaining its generalization capability.
\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Framework} \)
\( \text{ACM MM 2025} \)
We consider Latent Diffusion Models for Image Generation
Textual Inversion and DreamBooth as Personalization models

Diffusion Noise-Matching Loss
\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Framework} \)
\( \text{ACM MM 2025} \)
We consider Latent Diffusion Models for Image Generation
Textual Inversion and DreamBooth as Personalization models
Textual Inversion Loss

DreamBooth Loss
\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Framework} \)
\( \text{ACM MM 2025} \)
We consider Latent Diffusion Models for Image Generation
Textual Inversion and DreamBooth as Personalization models

where the personalization loss at the latent level is defined as
\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Framework} \)
\( \text{ACM MM 2025} \)
We consider Latent Diffusion Models for Image Generation
Textual Inversion and DreamBooth as Personalization models

Overall Loss:
\( \lambda \) - hyper-parameter
\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
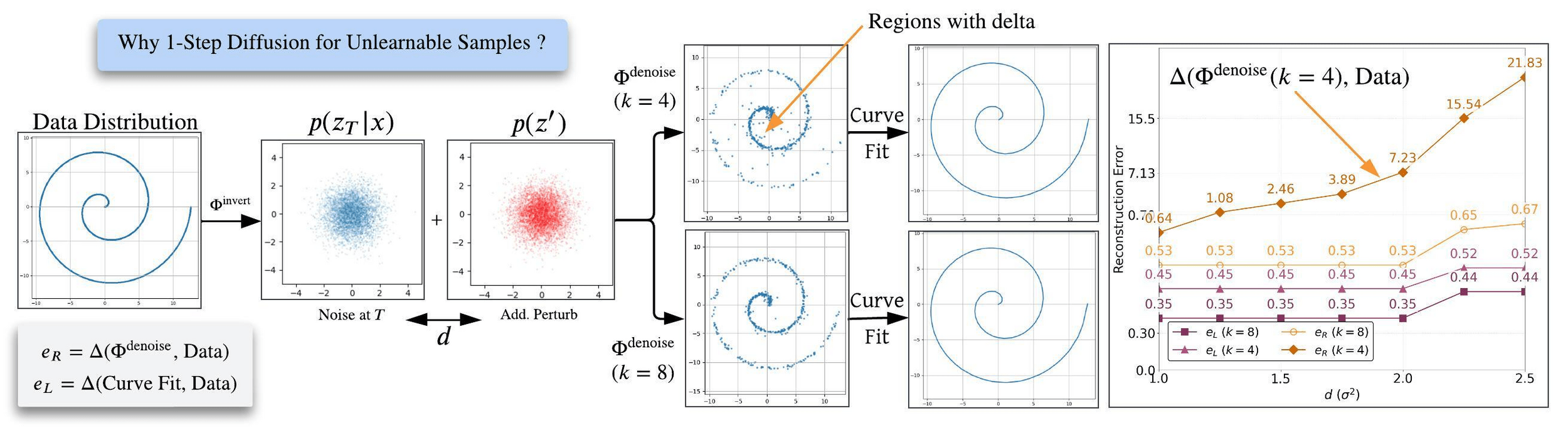
\( \textbf{Why 1-Step Diffusion} \)
\( \text{ACM MM 2025} \)
Few-step Diffusion Models maintain data distribution integrity while allowing perturbations in reconstruction:
\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Quantitative results across datasets} \)
\( \text{ACM MM 2025} \)
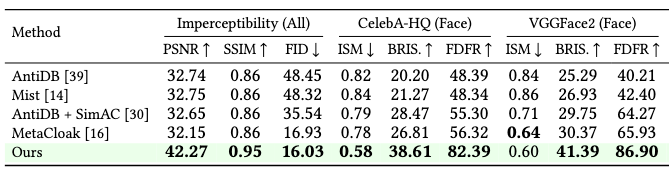
Quantitative results comparison to baseline methods: Metrics: (1) Imperceptibility (PSNR, SSIM, FID), (2) Face-specific metrics (ISM, BRIS, FDFR), (3) Non-Face metrics (SDS, ISM, BRIS, IQAC, LIQE). The metrics presented utilize \( 10/255 \) as the maximum budget, with \( 15 \) steps of DiffPure purification after Unlearnable Sample Generation and TI training with the prompt ``A photo of an sks person/object'' for personalization. We generate \( 16 \) images per prompt post personalization to report personalization metrics. We notice from the above table that our method shows significant improvements in imperceptible perturbation at the image-level while maintaining enhanced counter personalization metrics.
\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Qualitative Results} \)
\( \text{ACM MM 2025} \)

\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Robustness to Attacks} \)
\( \text{ACM MM 2025} \)


\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{Future Work} \)
\( \text{ACM MM 2025} \)
-
All Current unlearnable sample methods = static: perturbations crafted once after personalization model is fixed.
-
But real-world personalization is continual → models adapt incrementally.
-
Need defenses that also adapt continually to evolving personalization systems.
This min-max formulation can be written as:
This setup better reflects real-world usage, where users may upload new training data, and personalization systems are incrementally updated.
\( \text{Devulapally et al.} \)
\( \text{Latent Diffusion Unlearning} \)
\( \textbf{References} \)
\( \text{ACM MM 2025} \)
- Gal, R., Alaluf, Y., et al. An Image is Worth One Word: Personalizing Text-to-Image Generation using Textual Inversion. ICLR, 2023.
- Ruiz, N., Li, Y., et al. DreamBooth: Fine Tuning Text-to-Image Diffusion Models for Subject-Driven Generation. CVPR, 2023.
- Wen, R., Zhang, K. A., and Shokri, R. MetaCloak: Adversarial Cloaking against Black-box Personalized Diffusion Models. CVPR, 2024.
- Song, Y., Meng, C., and Ermon, S. Denoising Diffusion Implicit Models. NeurIPS, 2020.