Champs

How many matches does it take to find a champion?

On the number of comparisons we need to find the t-th best thing,

and notions of tournament solutions and their query complexity.

Prelude

The Setting · Total Orders and Tournaments

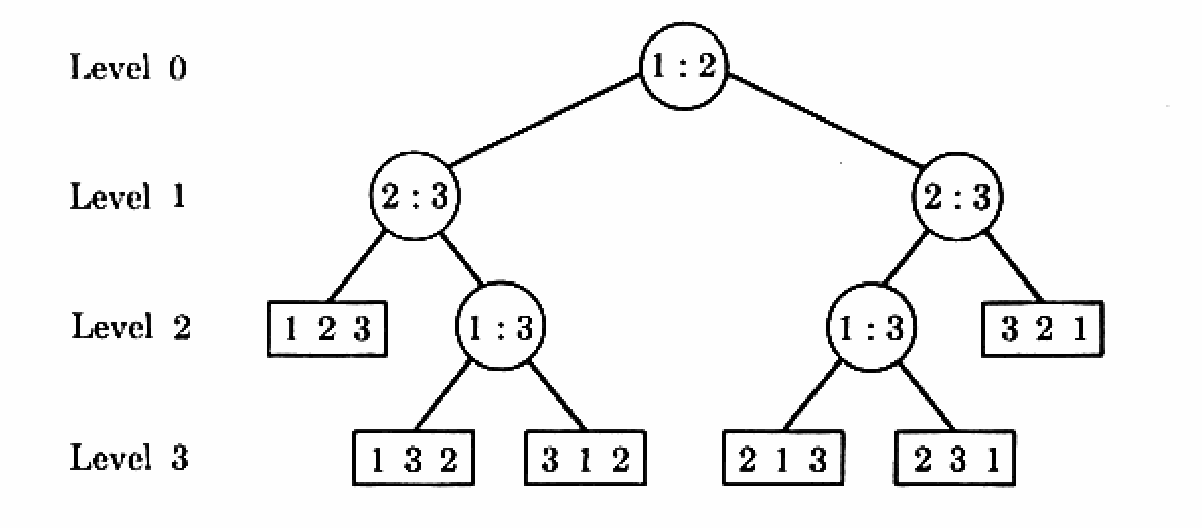
Comparison Tree

(borrowed from AoCP3)

pick two objects and compare · deduce underlying total order
optimize for number of comparisons

Best worst case measure.

Let \(S(n)\) be the minimum number of comparisons which will suffice to sort \(n\) elements.

\(B(n)=\sum_{1 \leq k \leq n}\left\lceil\log _2 k\right\rceil=n\left\lceil\log _2 n\right\rceil-2^{\left\lceil\log _2 n\right]}+1\)

Let \(B(n)\) be the number of comparisons used by
binary insertion sort.

Can five elements be sorted with 7 comparisons?

\(S(n) \geq\left\lceil\log _2 n!\right\rceil\).

Can five elements be sorted with 7 comparisons?

Phase 1: two comparisons between two disjoint pairs.

Can five elements be sorted with 7 comparisons?

Phase 1: two comparisons between two disjoint pairs.

Phase 2: compare the top elements between the chosen pairs.

Can five elements be sorted with 7 comparisons?

Phase 1: two comparisons between two disjoint pairs.

Phase 2: compare the top elements between the chosen pairs.

Phase 3: sneak in the third element on the 3-path for two comparisons.

Can five elements be sorted with 7 comparisons?

Phase 1: two comparisons between two disjoint pairs.

Phase 2: compare the top elements between the chosen pairs.

Phase 3: sneak in the third element on the 3-path for two comparisons.

Phase 4: have the last element find its place for two more comparisons.

Can five elements be sorted with 7 comparisons?

Yes.

The Merge-Insertion Method

\(F(n)=\lfloor n / 2\rfloor+F(\lfloor n / 2\rfloor)+G(\lceil n / 2\rceil)\)

\(F(n)=\sum_{1 \leq k \leq n}\left\lceil\log _2\left(\frac{3}{4} k\right)\right\rceil\)

(a) Pair up elements and find the higher ones among the pairs.

(b)Sort the top elements from the pairs
(using merge insertion).

The #ARRbracket on Twitter (2023)

Very different margins of victory

still lead to the same final outcome

in an unweighted setting.

Part - I

Finding the t-th largest among n elements

AoCP-3

[Dodgson] The second-best player wins second prize if and only if
he and the champion are originally in opposite halves of the tournament.

It is possible to win second prize even if you are worse than half of the players in the tournament.

In a mathematical seminar during 1929-1930, Hugo Steinhaus posed the problem of finding the minimum number of tennis matches required to determine the first and second best players in a tournament,
when there are \(n \geq 2\) players in all.

J. Schreier [Mathesis Polska 7 (1932), 154-160] gave a procedure which requires at most \(n-2+\left\lceil\log _2 n\right\rceil\) matches.

Schreier also claimed that \(n-2+\left\lceil\log _2 n\right\rceil\) is best possible, but his proof was incorrect, as was another attempted proof by J. Słupecki [Colloquium Mathematicum 2 (1951), 286-290].

Thirty-two years went by before a correct, although rather complicated, proof was finally published by S. S. Kislitsyn
[Sibirskiǐ Mat. Zhurnal 5 (1964), 557-564].

Let \(V_t(n)\) denote the minimum number of comparisons needed to determine the \(t\) th largest of \(n\) elements, for \(1 \leq t \leq n\).

Let \(W_t(n)\) be the minimum number required to determine the largest, second largest, . . . and \(t\) th largest, collectively.

\(V_{\mathbf{1}}(n) = W_1(n)\)

\(V_t(n) \leq W_t(n)\)

\(W_n(n) =W_{n-1}(n)=S(n)\)

Theorem. \(V_2(n)=W_2(n)=n-2+\left\lceil\log _2 n\right\rceil\), for \(n \geq 2\).

Claim 1. Can't find the runner up without finding the winner.

Theorem. \(V_2(n)=W_2(n)=n-2+\left\lceil\log _2 n\right\rceil\), for \(n \geq 2\).

Claim 1. Can't find the runner up without finding the winner.

Suppose not, and suppose the green player \(x\) is a declared runner up.

Theorem. \(V_2(n)=W_2(n)=n-2+\left\lceil\log _2 n\right\rceil\), for \(n \geq 2\).

Claim 1. Can't find the runner up without finding the winner.

Suppose not, and suppose the green player \(x\) is a declared runner up.

There must exist a player \(y\) who we have not compared \(x\) with yet.

But then we can be consistent with either \(x > y\) or \(x < y\),
leaving the second winner position ambiguous.

Theorem. \(V_2(n)=W_2(n)=n-2+\left\lceil\log _2 n\right\rceil\), for \(n \geq 2\).

Assume that \(n\) players have participated in a tournament which has determined the second-best player by some given procedure, and let \(a_j\) be the number of players who have lost \(j\) or more matches.

The total number of matches played is then \(a_1+a_2+a_3+\cdots\).

\(a_1=n-1\).

To complete the proof, we will show that there is always some sequence of outcomes of the matches which makes \(a_2 \geq\left\lceil\log _2 n\right\rceil-1\)

Theorem. \(V_2(n)=W_2(n)=n-2+\left\lceil\log _2 n\right\rceil\), for \(n \geq 2\).

Suppose that at the end of the tournament the champion has played (and beaten) \(p\) players.

One of these is the second best,
and the others must have lost at least one other time, so \(a_2 \geq p-1\).

Therefore we can complete the proof by finding an adversary who decides the results of the games in such a way that the champion must play at Ieast \(\left\lceil\log _2 n\right\rceil\) other people.

Theorem. \(V_2(n)=W_2(n)=n-2+\left\lceil\log _2 n\right\rceil\), for \(n \geq 2\).

Therefore we can complete the proof by finding an adversary who decides the results of the games in such a way that the champion must play at Ieast \(\left\lceil\log _2 n\right\rceil\) other people.

Let the adversary declare \(A\) to be better than \(B\)

if \(A\) is previously undefeated and \(B\) has lost at least once,

or if both are undefeated and \(B\) has won fewer matches than \(A\) at that time.

In other circumstances the adversary may make an arbitrary decision consistent with some partial ordering.

Let us say that \(A\) supersedes \(B\) if and only if \(A=B\) or \(A\) supersedes the player who first defeated \(B\).

Theorem. \(V_2(n)=W_2(n)=n-2+\left\lceil\log _2 n\right\rceil\), for \(n \geq 2\).

It follows that a player who won his first \(p\) matches supersedes at most \(2^p\) players on the basis of those \(p\) contests.

Let us say that \(A\) supersedes \(B\) if and only if \(A=B\) or \(A\) supersedes the player who first defeated \(B\).

The champion supersedes everyone, so
s/he must have played at least \(\left\lceil\log _2 n\right\rceil\) matches.

Let the adversary declare \(A\) to be better than \(B\)

if \(A\) is previously undefeated and \(B\) has lost at least once,

or if both are undefeated and \(B\) has won fewer matches than \(A\) at that time.

In other circumstances the adversary may make an arbitrary decision consistent with some partial ordering.

\(W_t(n) \leq n-t+\sum_{n+1-t<j \leq n}\left\lceil\log _2 j\right\rceil, \quad\) for \(\quad n \geq t\).

For general \(t\), it can be shown that:

More recent work* tackles a generalization to \(k\)-way comparisons.

*Variations on the Tournament Problem, FUN 2024

Part - II

Tournaments: who are the best candidates, anyway?

Who wins a tournament?

A tournament solution is a function \({\color{IndianRed}\mathfrak{f}}\) that maps each tournament \(T=(A, \succ)\) to a nonempty subset \({\color{IndianRed}\mathfrak{f}(T)}\) of the alternatives \(A\) (called the choice set), and
does not distinguish between isomorphic tournaments.

If there is a player \(c\) who beats every other player, then \(c\) is a Condorcet winner.

If there is a player \(c\) who wins against at least one player, then \(c\) is a Condorcet non-loser.

If there is a player \(c\) who loses to every other player, then \(c\) is a Condorcet loser.

The top cycle set is defined as the smallest set such that every candidate inside the set S is pairwise unbeaten by every candidate outside S.

Alternatively, it can be defined as the set of all candidates with a (non-strict) beatpath to any candidate who defeats them.

Well-defined · Condorcet-consistent

Generalizing Condorcet Winners

The Copeland set \(\operatorname{CO}(T)\) of a tournament \(T\) consists of all alternatives whose dominion is of maximal size, that is,

\(CO(T)=\arg \max _{a \in A}|D(a)|.\)

\(|D(a)|\) is also called the Copeland score of \(a\).

Note that \(|D(a)|\) is the outdegree of vertex \(a\).

Denote the maximal element of \(A\) according to a strict linear order \(>\) by \(\max (>)\).

The Slater score of a strict linear order \(>\) over the alternatives in \(A\) with respect to tournament \(T=(A, \succ)\) is \(|>\cap \succ|\).

A strict linear order is a Slater order if it has maximal Slater score. Then, the Slater set \(S L\) is defined as

\(SL(T)=\{\max (>): ~>\text { is a Slater order for } T\}.\)

With the Slater set, we are interested in a
linearization that preserves as many edges as possible.

The Banks set selects the maximal elements of all maximal transitive subtournaments.

A transitive subtournament \(\left(B, \succ_B\right)\) of tournament \(T\) is said to be maximal if there is no other transitive subtournament \(\left(C, \succ_C\right)\) of \(T\) with \(B \subset C\).

With the Banks set, we are interested in
maximal transitive subtournaments.

The Banks set \(B A(T)\) of a tournament is then defined as

\(\left\{\max \left(\succ_B\right):\left(B, \succ_B\right) \text { is a maximal transitive subtournament of } T\right\} .\)

Part - III

Querying Tournaments

Query Complexity of Tournament Solutions
Arnab Maiti and Palash Dey

Given a tournament \(\mathcal{T}=(\mathcal{V}, \mathcal{E})\) on \(n\) vertices, a query for a pair of vertices \(\{x, y\}\) reveals whether \(x < y\) or \(y < x\).

The query complexity of an algorithm is the maximum number of queries the algorithm makes in the worst case.

The query complexity of a tournament solution \(\mathfrak{f}\) is the minimum query complexity of any algorithm for computing \(\mathfrak{f}\).

Recap

Warmup: The query complexity of finding the Condorcet winner
and the Condorcet non-loser set is \(2 n-\lfloor\log n\rfloor-2\).

upper bound. Knockout (\(n-1\)) followed by validation \((n-1-\lfloor \log n \rfloor)\).

For Condorcet winner:

lower bound. Adapt the ideas from before (for finding the second-max).

For Condorcet non-loser:

Flip the tournament.

The Regular Tournament

Place \(n = 2k+1\) candidates around a circle,

and have each candidate win against the next \(k\)
and lose to the previous \(k\).

The Copeland set and the Slater set contain all vertices in \(T_r\).

Suppose the out-degree of a vertex \(\mathcal{v} \in \mathcal{V}\) in a tournament
\(\mathcal{T}=(\mathcal{V}, \mathcal{E})\) on \(n\) vertices is strictly less than \((n-1) / 2\).

Then \(v\) does not belong to the Slater set of \(\mathcal{T}\).

If there is a linear order where \(v\) comes out on top, there is another one where it is cheaper to position \(v\) at the bottom.

The Almost Regular Tournament

Consider \(T_r^{uv}\), which is the same as \(T_r\) except with the edge \(uv\) flipped.

The candidate \(u\) does not belong to the Copeland set or the Slater set.

Let \(\mathcal{T}\) be a tournament whose top cycle is \(\mathcal{C}\).

Then the Copeland set, the Slater set and the Banks set of \(\mathcal{T}\) are the same as the corresponding solutions for the tournament \(\mathcal{T}(\mathcal{C})\) which is the tournament \(\mathcal{T}\) restricted to \(\mathcal{C}\).

There is a \(\Omega(n^2)\) lower bound on the query complexity of the Banks set.

open direction: can we do better on structured tournaments?