Binary Black Holes
A GENERIC Approach
Ref Bari
Advisor: Prof. Brendan Keith


Binary Black Holes
A GENERIC Approach
- Optimize Parameter Estimation
- Circular Orbit
- Elliptical Orbit
- Eccentric Orbit
- Butterfly Orbit
- Created Hamiltonian Neural Network!

Binary Black Holes
A GENERIC Approach

- Optimize Parameter Estimation
- Circular Orbit
- Elliptical Orbit
- Eccentric Orbit
- Butterfly Orbit
- Created Hamiltonian Neural Network!
Optimize Parameter Estimation
- Optimal Learning Rate?
- Optimal # Epochs?
- Optimal Training Fraction?
- Optimal Number of Partitions?
- Best Anstazs?
- Sensitivity to Initial Guess?
\texttt{optimizeBlackHole}
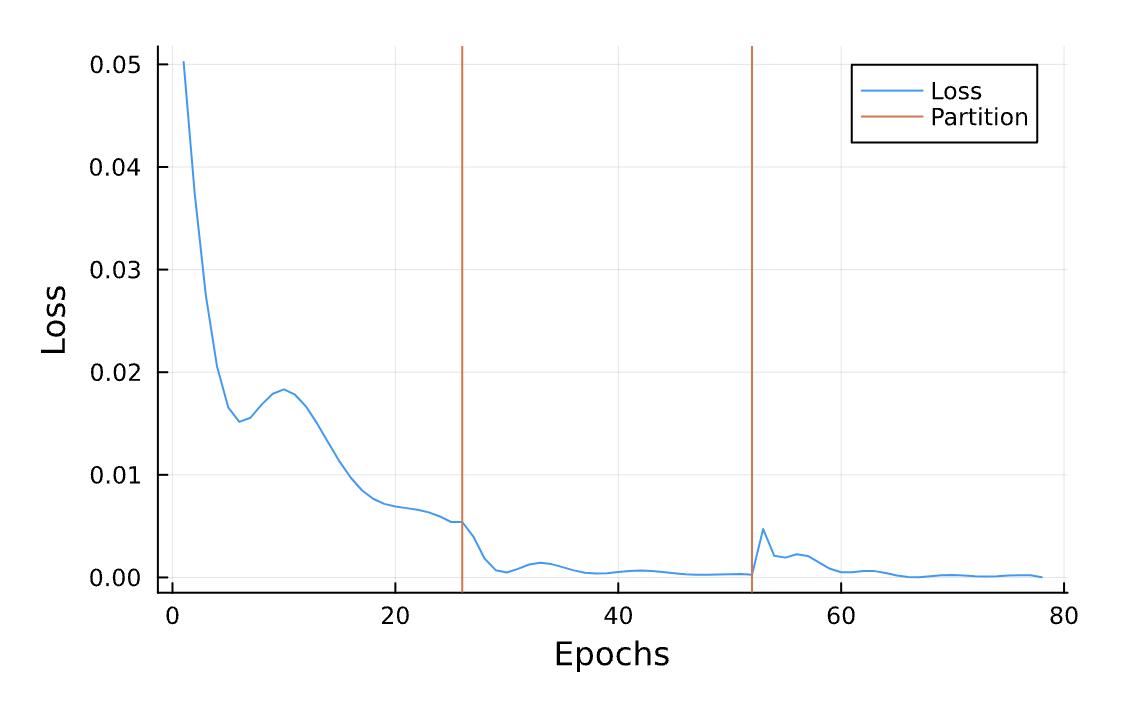
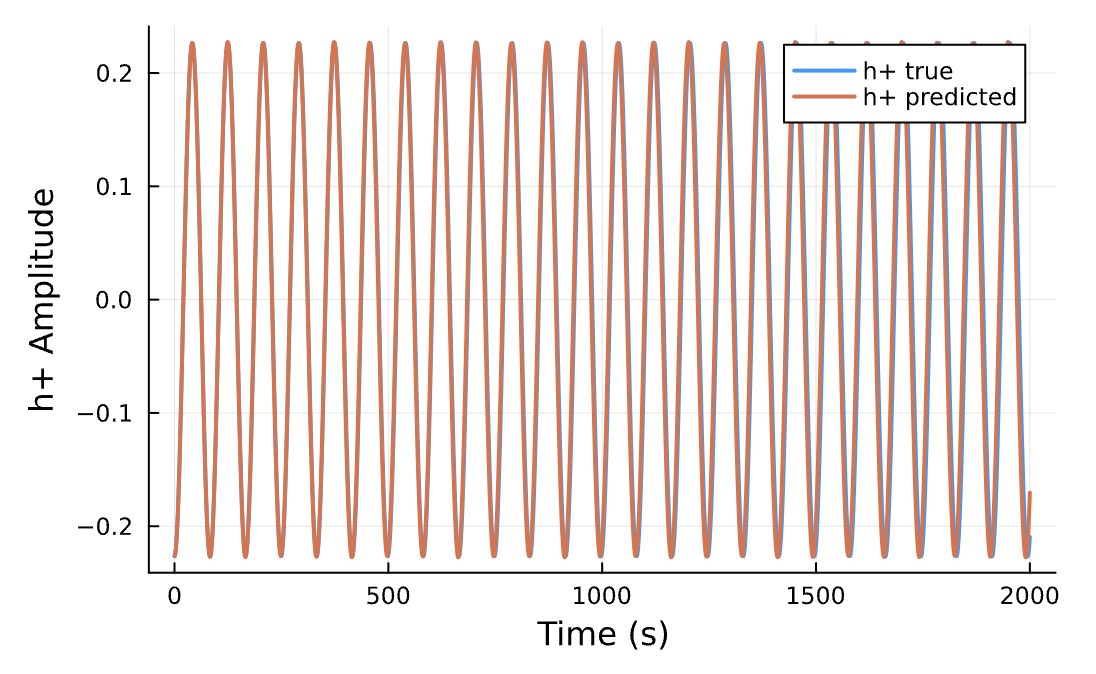
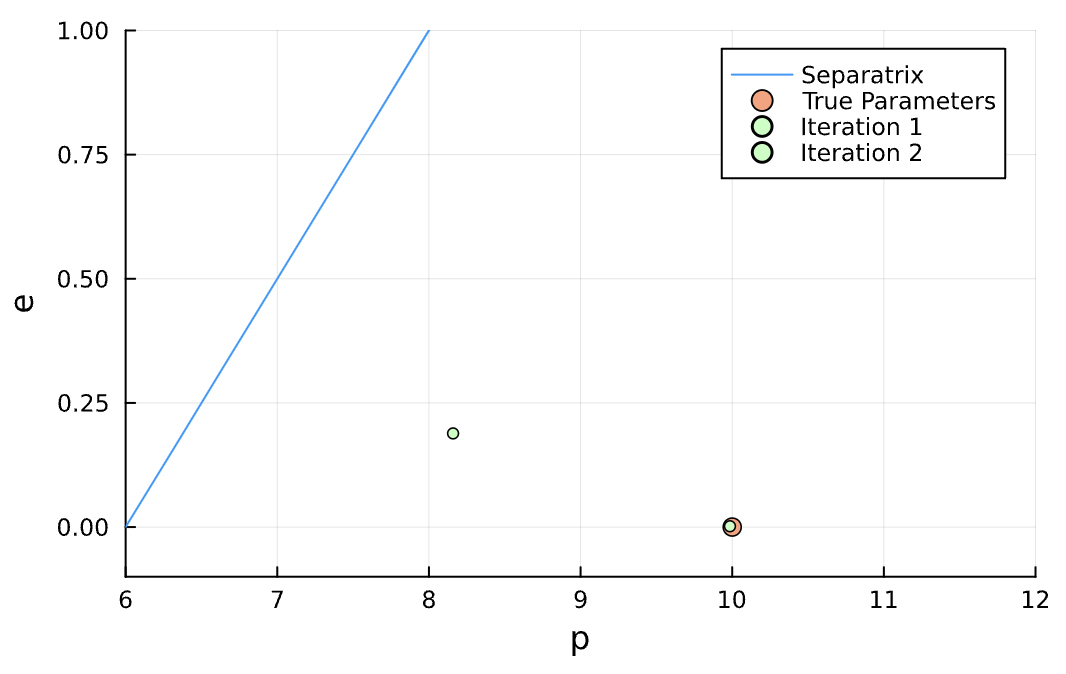
Black Hole Orbits
Gravitational Wave
Loss Function
Plane
(p,e)



Circular Orbit
Gravitational Wave
Loss Function
Plane
(p,e)



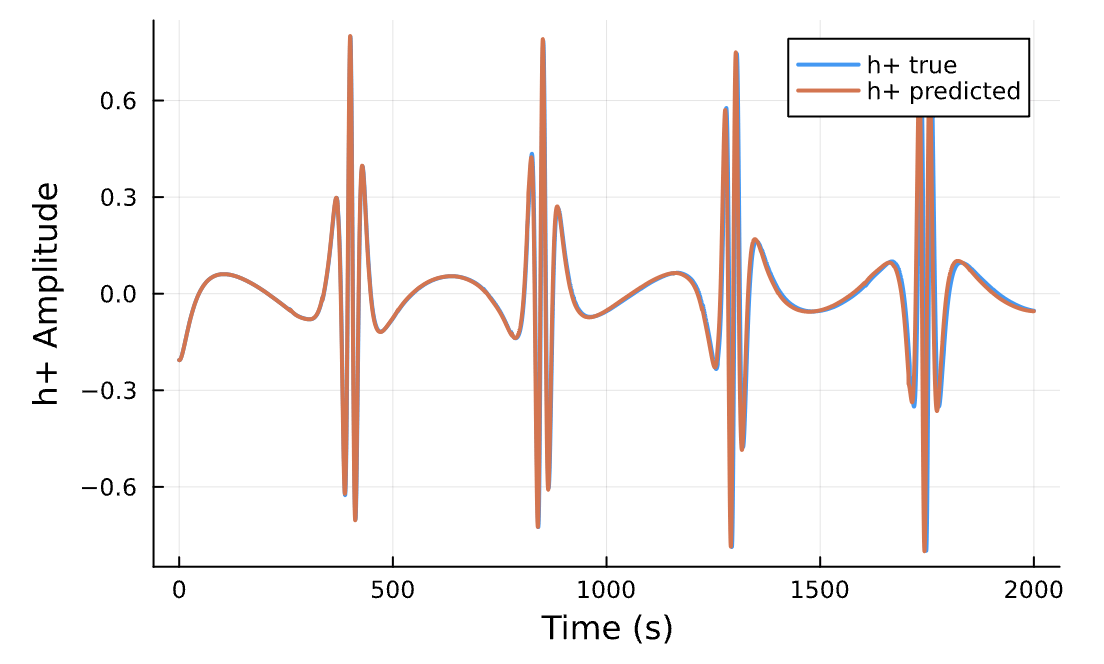
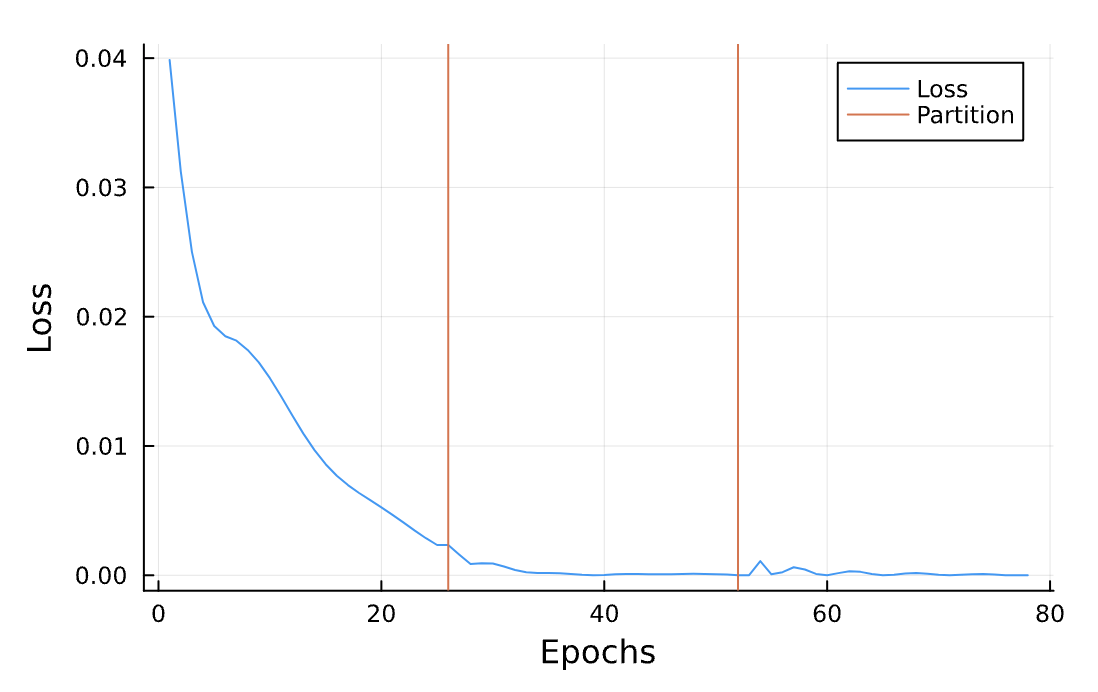
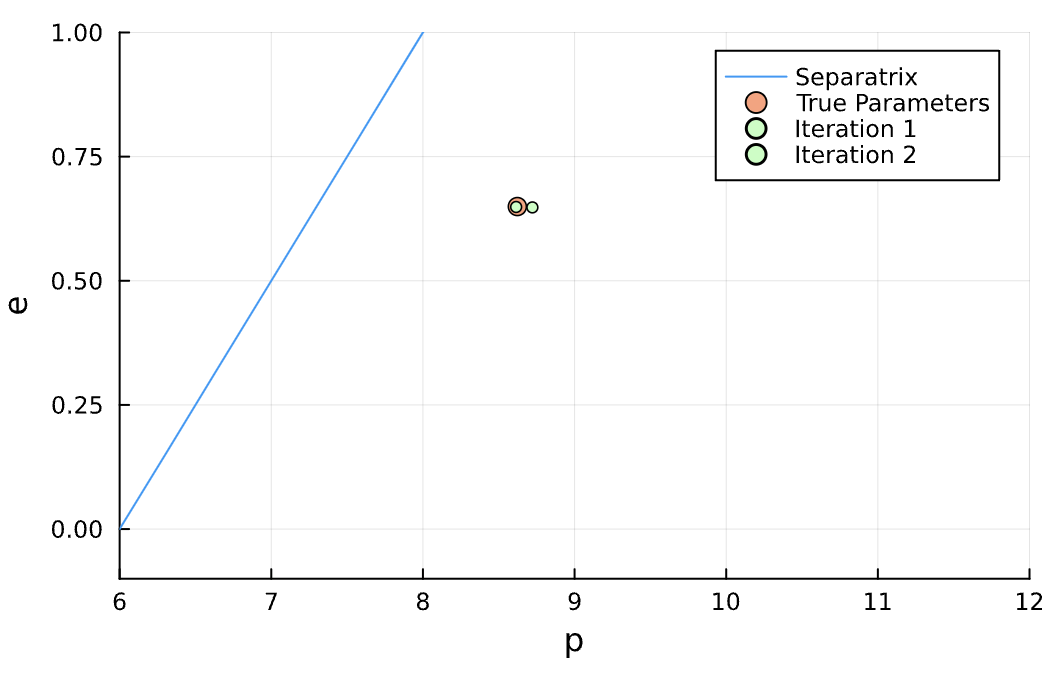
Elliptical Orbit
Gravitational Wave
Loss Function
Plane
(p,e)






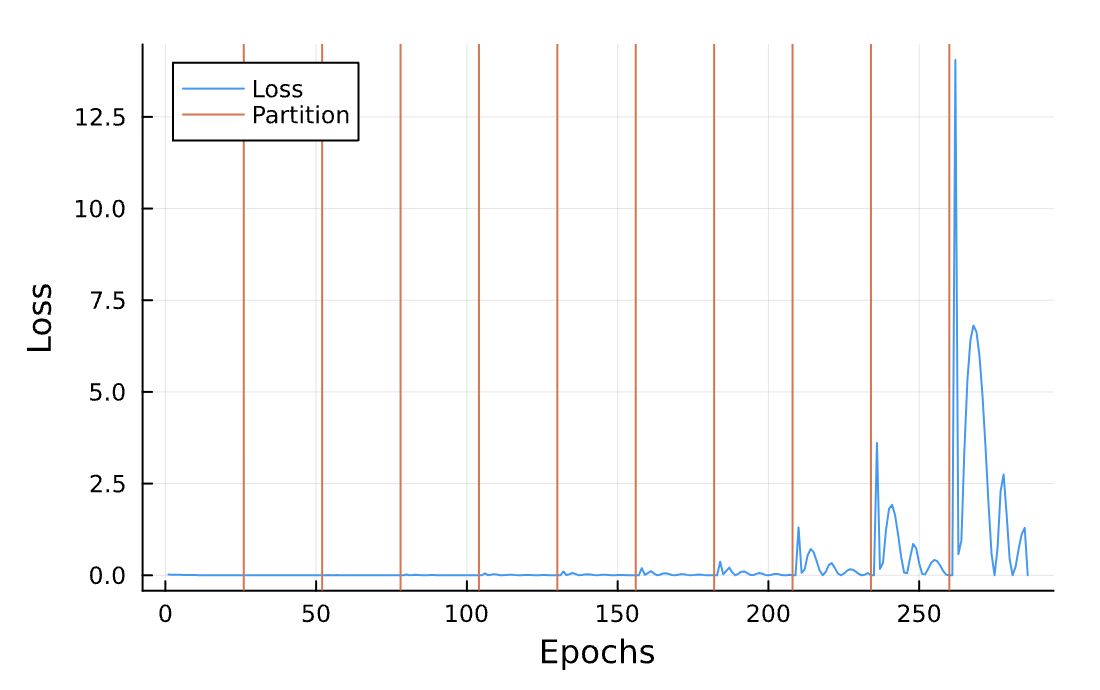
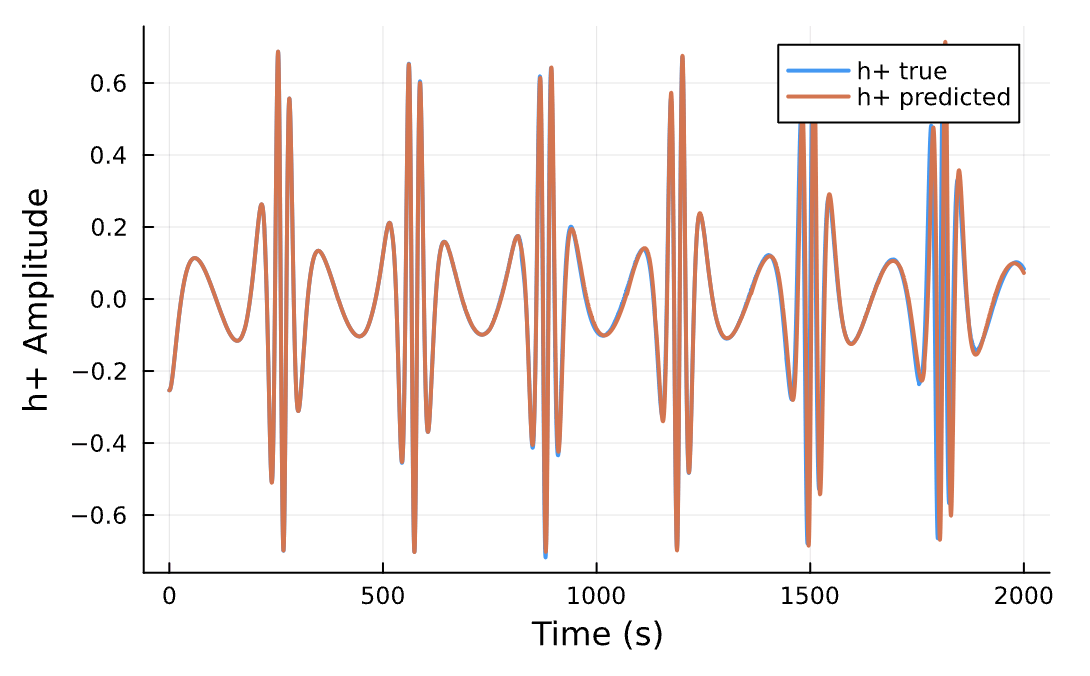
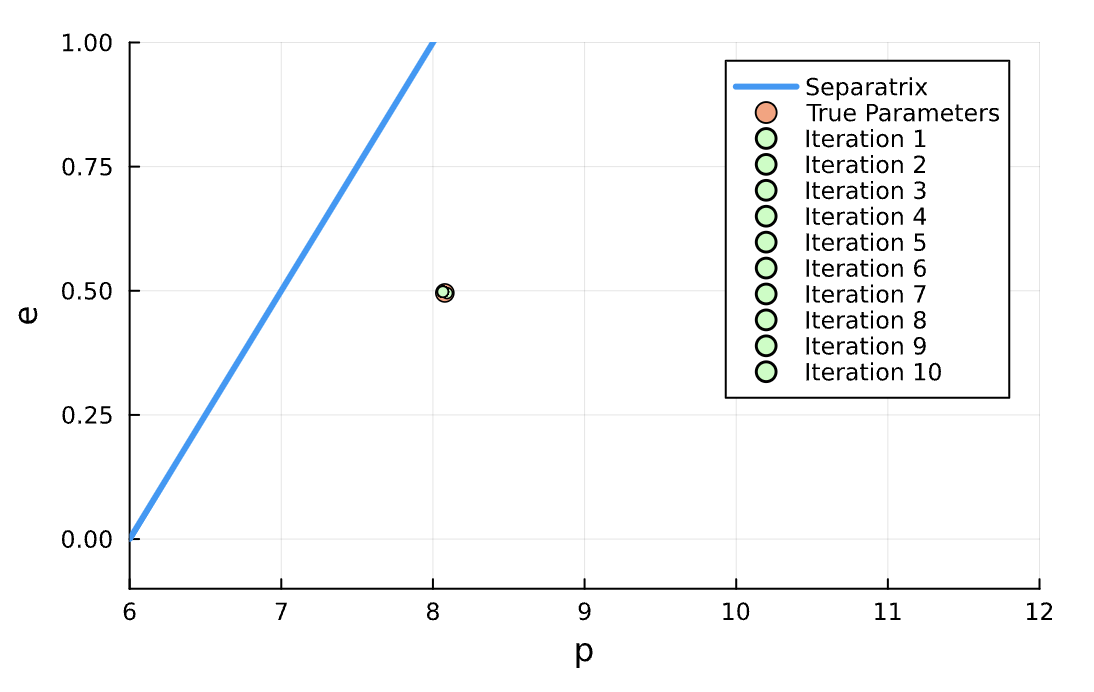
Highly Eccentric Orbit
Gravitational Wave
Loss Function
Plane
(p,e)
Butterfly Orbit
Gravitational Wave
Loss Function
Plane
(p,e)
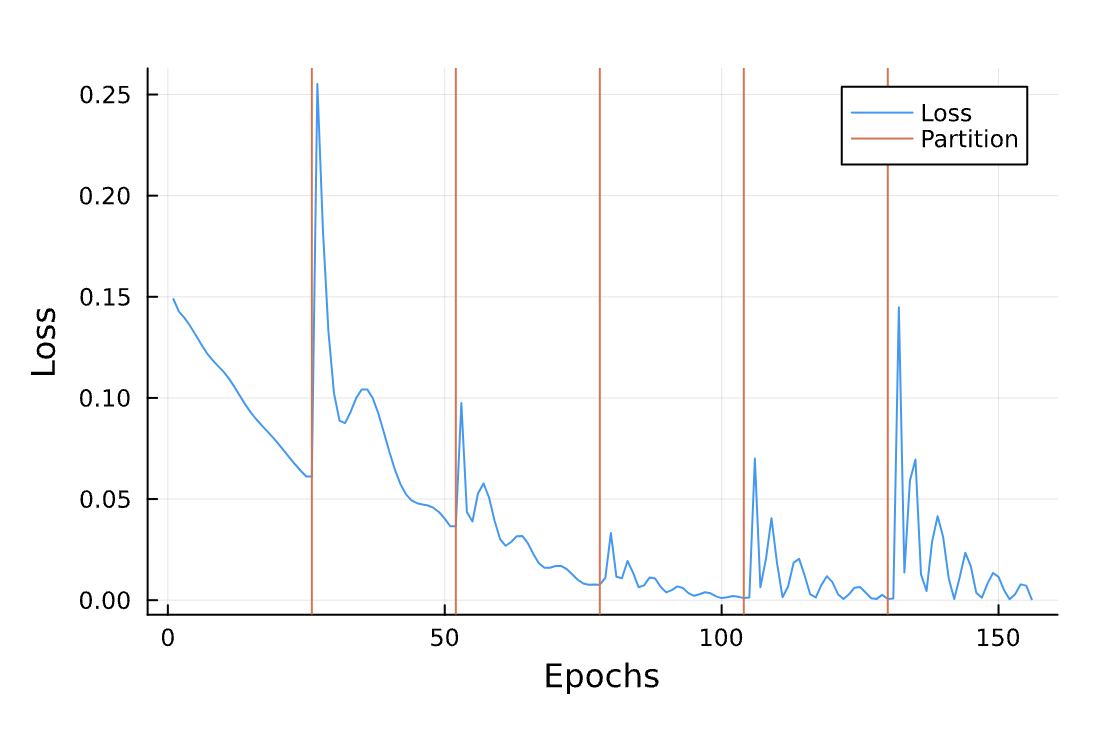
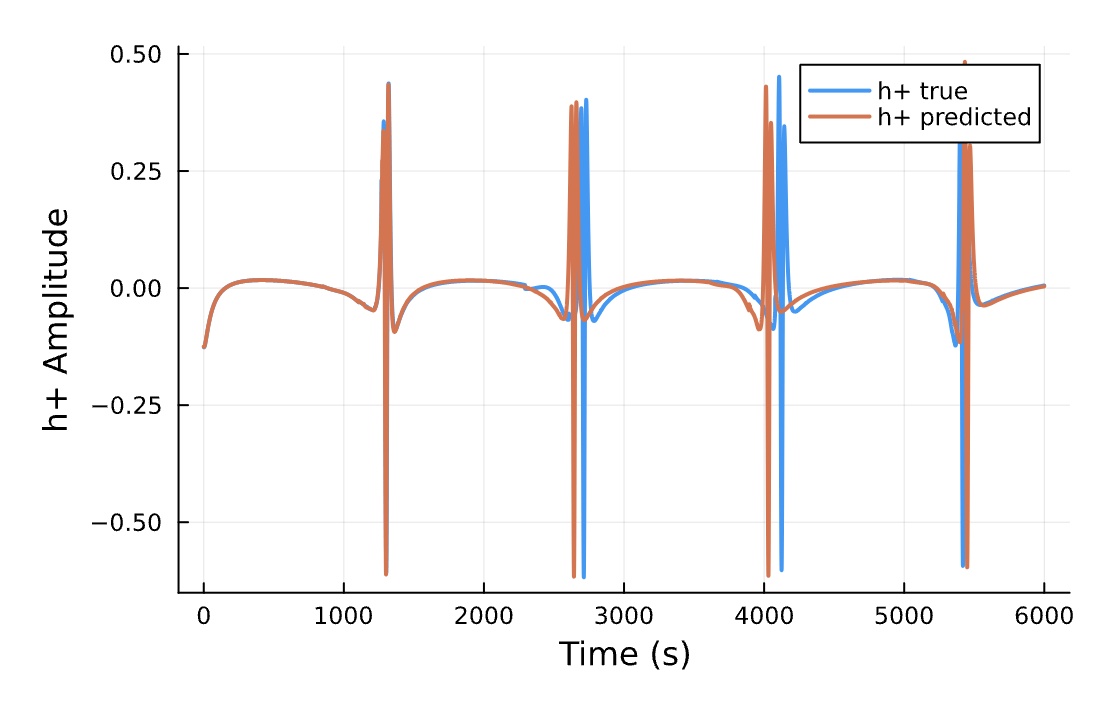
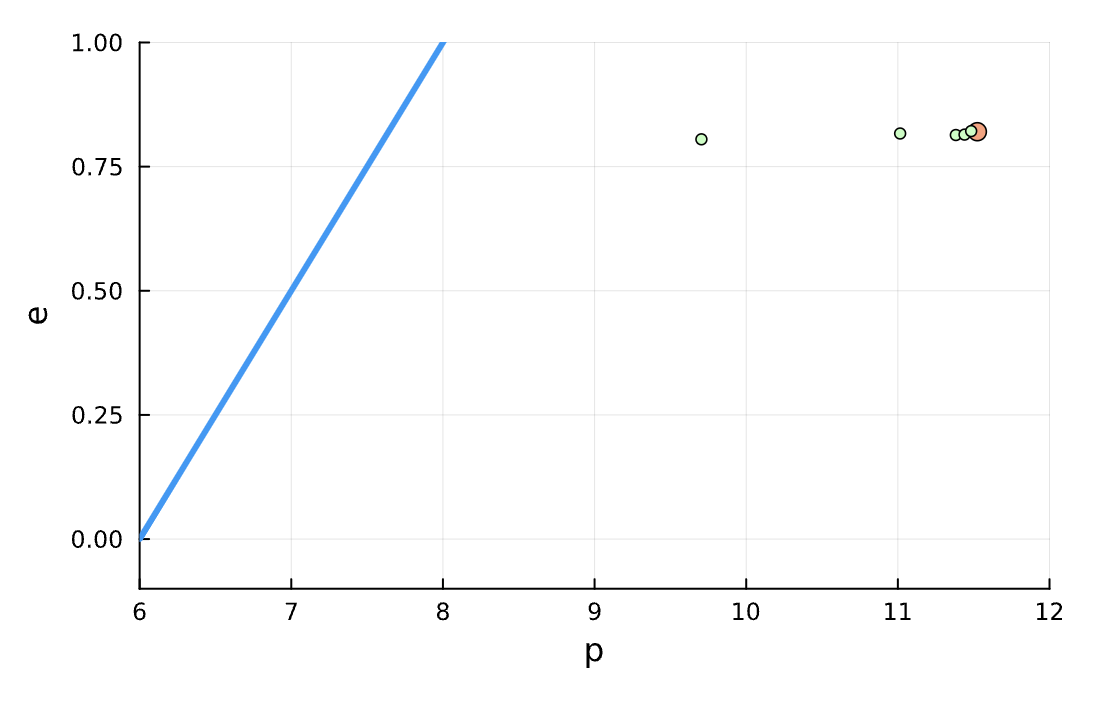
Optimize Parameter Estimation*
\texttt{optimizeBlackHole}
*This was a failed attempt, sadly
Optimize Parameter Estimation
\texttt{optimizeBlackHole(lr, epochs, numCyles, totalTraining\%},p_0\texttt{)}
\texttt{lr}
\texttt{epochs}
\texttt{numCyles}
\texttt{totalTraining\%}
p_0
Optimize Parameter Estimation
\texttt{optimizeBlackHole(lr, epochs, numCyles, totalTraining\%},p_0\texttt{)}
\texttt{lr}: \text{Learning Rate}
\texttt{epochs}: \text{\# Epochs per Cycle}
\texttt{numCyles}: \text{Number of Cycles (numCycles = n} \to n+1 {\text{ Opt Runs)}}
\texttt{totalTraining\%}: \text{\% Training Data given to Optimizer}
p_0: \text{Initial Guess for } (M,E,L)
Hamiltonian Neural Network!
H_{Kepler}
H_{Schwarzschild}
Hamiltonian Neural Network!
H_{Kepler} = \frac{p_r^2}{2}-\frac{M}{r}+\frac{L^2}{2r^2}
\begin{align*}
H_{Schwarzschild} = -&\frac{1}{2}\left(1-\frac{2M}{r}\right)^{-1}E^2+
\frac{1}{2}\left(1-\frac{2M}{r}\right)(p_r)^2+
\frac{L^2}{2r^2}\end{align*}
H_s = H_k + \mathcal{f}_{NN}
Hamiltonian Neural Network!
H_kep = p_r^2/2 - M/r + L^2/(2*r^2)NN_correction = NN([r, p_r, L], NN_params, NN_state)[1][1]H_total(r_val, pr_val) = pr_val^2/2 - M/r_val + L^2/(2*r_val^2) + NN_correctionHamiltonian Neural Network!
function SchwarzschildNN_Hamiltonian(du, u, p, t)
coord_time, r, θ, ϕ, p_t, p_r, p_θ, p_ϕ = u
M = p.M
E = p.E
L = p.L
NN_params = p.NN
# Kepler Hamiltonian
H_kep = p_r^2/2 - M/r + L^2/(2*r^2)
# NN Correction
NN_correction = NN([r, p_r, L], NN_params, NN_state)[1][1]
# Total Hamiltonian
H_total(r_val, pr_val) = pr_val^2/2 - M/r_val + L^2/(2*r_val^2) + NN_correction
# Hamilton's equations
du[1] = 1.0 # Simple time evolution
du[2] = ForwardDiff.derivative(pr -> H_total(r, pr), p_r) # ṙ = ∂H/∂p_r
du[3] = 0
du[4] = L/r^2
du[5] = 0
du[6] = -ForwardDiff.derivative(r_val -> H_total(r_val, p_r), r) # ṗ_r = -∂H/∂r
du[7] = 0
du[8] = 0
endHamiltonian Neural Network!
function SchwarzschildNN_Hamiltonian(du, u, p, t)
coord_time, r, θ, ϕ, p_t, p_r, p_θ, p_ϕ = u
M = p.M
E = p.E
L = p.L
NN_params = p.NN
# Kepler Hamiltonian
H_kep = p_r^2/2 - M/r + L^2/(2*r^2)
# NN Correction
NN_correction = NN([r, p_r, L], NN_params, NN_state)[1][1]
# Total Hamiltonian
H_total(r_val, pr_val) = pr_val^2/2 - M/r_val + L^2/(2*r_val^2) + NN_correction
# Hamilton's equations
du[1] = 1.0 # Simple time evolution
du[2] = ForwardDiff.derivative(pr -> H_total(r, pr), p_r) # ṙ = ∂H/∂p_r
du[3] = 0
du[4] = L/r^2
du[5] = 0
du[6] = -ForwardDiff.derivative(r_val -> H_total(r_val, p_r), r) # ṗ_r = -∂H/∂r
du[7] = 0
du[8] = 0
endHamiltonian Neural Network!
function SchwarzschildNN_Hamiltonian(du, u, p, t)
coord_time, r, θ, ϕ, p_t, p_r, p_θ, p_ϕ = u
M = p.M
E = p.E
L = p.L
NN_params = p.NN
# Kepler Hamiltonian
H_kep = p_r^2/2 - M/r + L^2/(2*r^2)
# NN Correction
NN_correction = NN([r, p_r, L], NN_params, NN_state)[1][1]
# Total Hamiltonian
H_total(r_val, pr_val) = pr_val^2/2 - M/r_val + L^2/(2*r_val^2) + NN_correction
# Hamilton's equations
du[1] = 1.0 # Simple time evolution
du[2] = ForwardDiff.derivative(pr -> H_total(r, pr), p_r) # ṙ = ∂H/∂p_r
du[3] = 0
du[4] = L/r^2
du[5] = 0
du[6] = -ForwardDiff.derivative(r_val -> H_total(r_val, p_r), r) # ṗ_r = -∂H/∂r
du[7] = 0
du[8] = 0
endHamiltonian Neural Network!
function SchwarzschildNN_Hamiltonian(du, u, p, t)
coord_time, r, θ, ϕ, p_t, p_r, p_θ, p_ϕ = u
M = p.M
E = p.E
L = p.L
NN_params = p.NN
# Kepler Hamiltonian
H_kep = p_r^2/2 - M/r + L^2/(2*r^2)
# NN Correction
NN_correction = NN([r, p_r, L], NN_params, NN_state)[1][1]
# Total Hamiltonian
H_total(r_val, pr_val) = pr_val^2/2 - M/r_val + L^2/(2*r_val^2) + NN_correction
# Hamilton's equations
du[1] = 1.0 # Simple time evolution
du[2] = ForwardDiff.derivative(pr -> H_total(r, pr), p_r) # ṙ = ∂H/∂p_r
du[3] = 0
du[4] = L/r^2
du[5] = 0
du[6] = -ForwardDiff.derivative(r_val -> H_total(r_val, p_r), r) # ṗ_r = -∂H/∂r
du[7] = 0
du[8] = 0
endHamiltonian Neural Network!
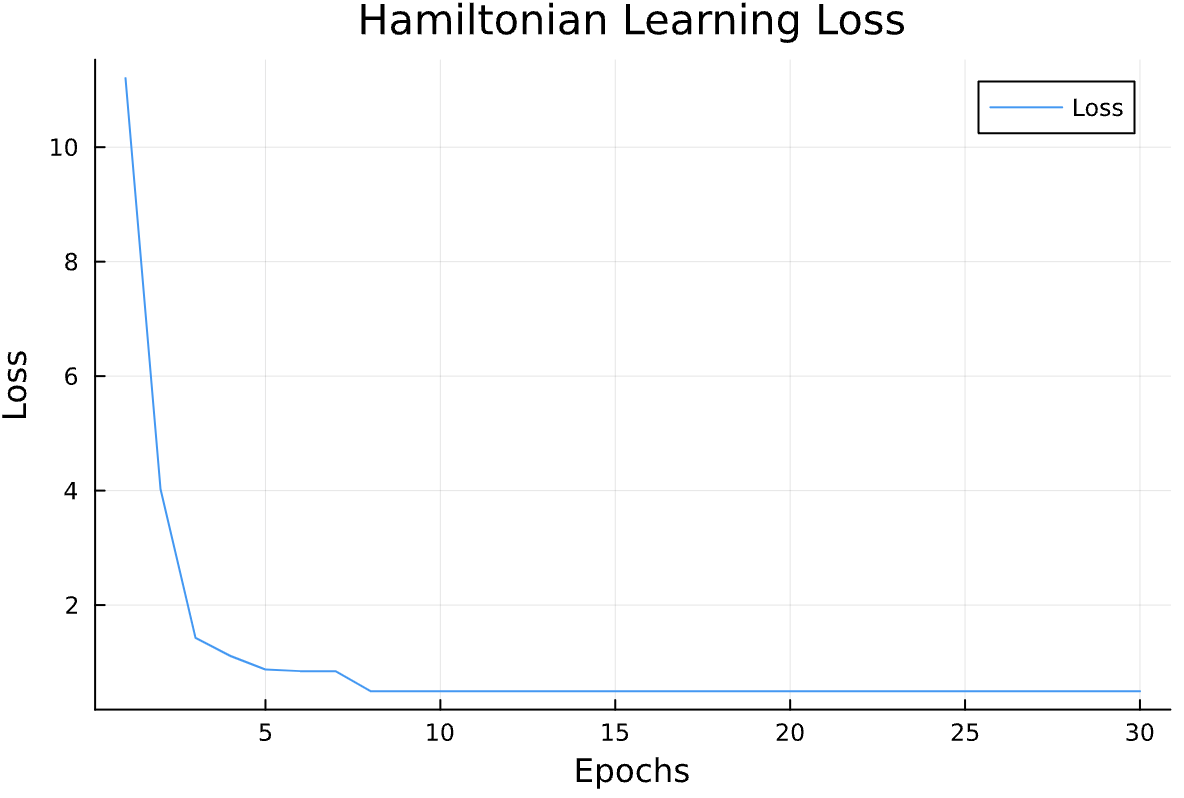
Hamiltonian Neural Net
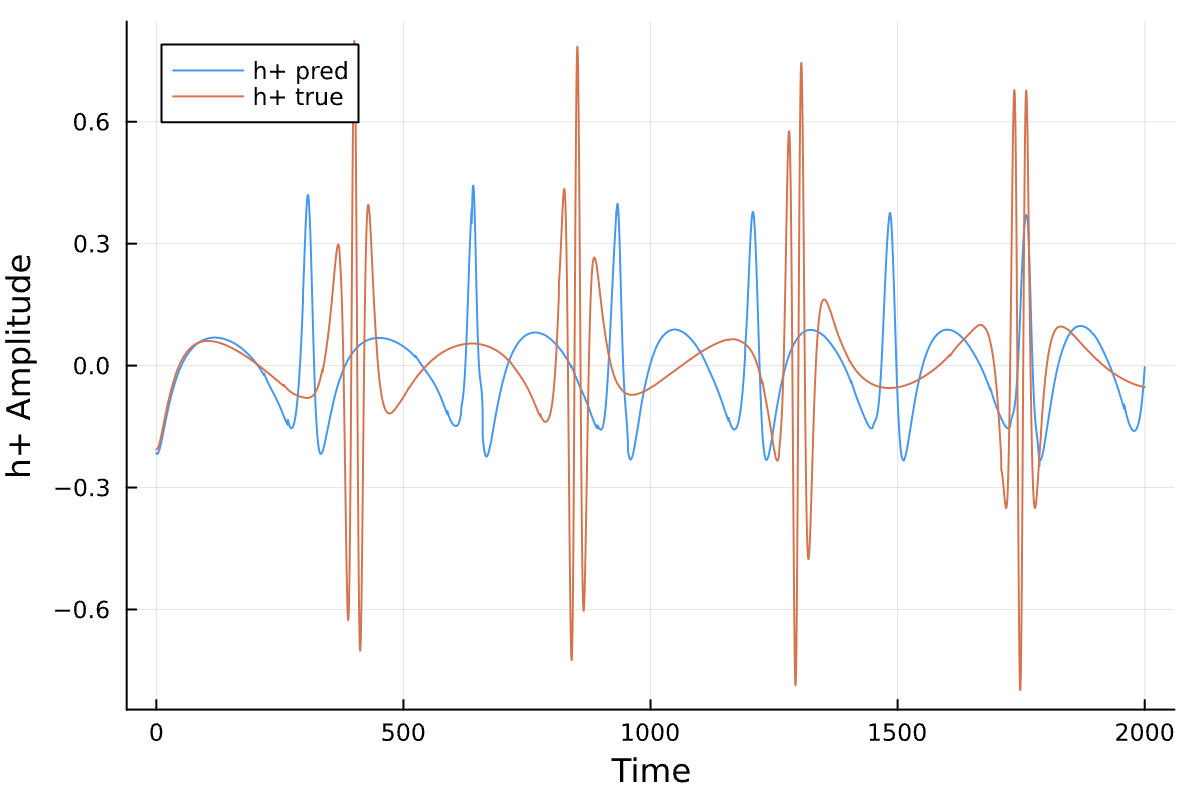
Binary Black Holes | 07/03 Update
By Ref Bari
Binary Black Holes | 07/03 Update
- 188


