Binary Black Holes

A GENERIC Approach

Ref Bari

Advisor: Prof. Brendan Keith

The Goal

H_{Kepler} = \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2} - \frac{M}{r}

The Goal

H_{Kepler} = \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2} - \frac{M}{r}

H_{Schwarzschild} = - \left(1-\frac{2M}{r}\right)^{-1}\frac{p_t^2}{2} + \left(1-\frac{2M}{r}\right) \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2}

The Goal

H_{Kepler} = \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2} -\frac{p_t^2}{2} = (1,1,-1)\cdot (\frac{p_r^2}{2}, \frac{p_\phi^2}{2r^2}, \frac{p_t^2}{2} )

H_{Schwarzschild} = - \left(1-\frac{2M}{r}\right)^{-1}\frac{p_t^2}{2} + \left(1-\frac{2M}{r}\right) \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2}

H_{Schwarzschild} =-\frac{p_t^2}{2}+\frac{p_r^2}{2}+\frac{p_{\phi}^2}{2r^2}

\frac{\partial H_{kepler}}{\partial p_t} = -p_t \to \frac{dt}{d\tau}=\frac{\partial H_{kepler}}{\partial p_t}=-p_t=-E \to \frac{dt}{d\tau} = \frac{E}{1-2M/r} \\ H_{total} = H_{kepler}+f_{NN}

p=(p_r, p_{\phi}, p_t) \to H = \frac{1}{2}p^T Mp \to M = \text{diag}(1, 1/r^2, -1) \to g_{total} = g_{Kep} + g_{NN}(r)

H = \frac{1}{2}p^T Mp \to M = \text{diag}\left(-\left(1-\frac{2}{r}\right)^{-1}, \left(1-\frac{2}{r}\right), -1\right)

M=M(u)=M(r, \phi) = M(r) = \frac{p^\mu p_\mu}{2}=g^{\mu\nu}p_{\mu}p_{\nu}/2

The Goal

H_{Schwarzschild} = - \left(1-\frac{2M}{r}\right)^{-1}\frac{p_t^2}{2} + \left(1-\frac{2M}{r}\right) \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2}

g^{\mu \nu}=\begin{pmatrix} -\left(1-\frac{2M}{r}\right)^{-1} & 0 & 0 & 0\\ 0 & \left(1-\frac{2M}{r}\right) & 0 & 0 \\ 0 & 0 & r^{-2} & 0 \\ 0 & 0 & 0 & r^{-2} \end{pmatrix}

g^{\mu \nu}=\begin{pmatrix} -f^{-1} & 0 & 0 & 0\\ 0 & f & 0 & 0 \\ 0 & 0 & r^{-2} & 0 \\ 0 & 0 & 0 & r^{-2} \end{pmatrix}

g^{00}g^{11}=-1

The Goal

H_{Kepler} = \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2} - \frac{M}{r}

H_{Schwarzschild} = - \left(1-\frac{2M}{r}\right)^{-1}\frac{p_t^2}{2} + \left(1-\frac{2M}{r}\right) \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2}

-\left(1-\frac{2M}{r}\right)^{-1} \frac{p_t^2}{2}

\left(1-\frac{2M}{r}\right)

\frac{p_r^2}{2} + \frac{p_φ^2}{2r^2}

Conserved Quantities:

\dot{H} = 0, \dot{E} = 0, \dot{L} = 0

Latest Results

Learning Rate = 7e-3, Epochs = 6, # Iterations = 6, Training = 5% ~ 100/2000 time steps

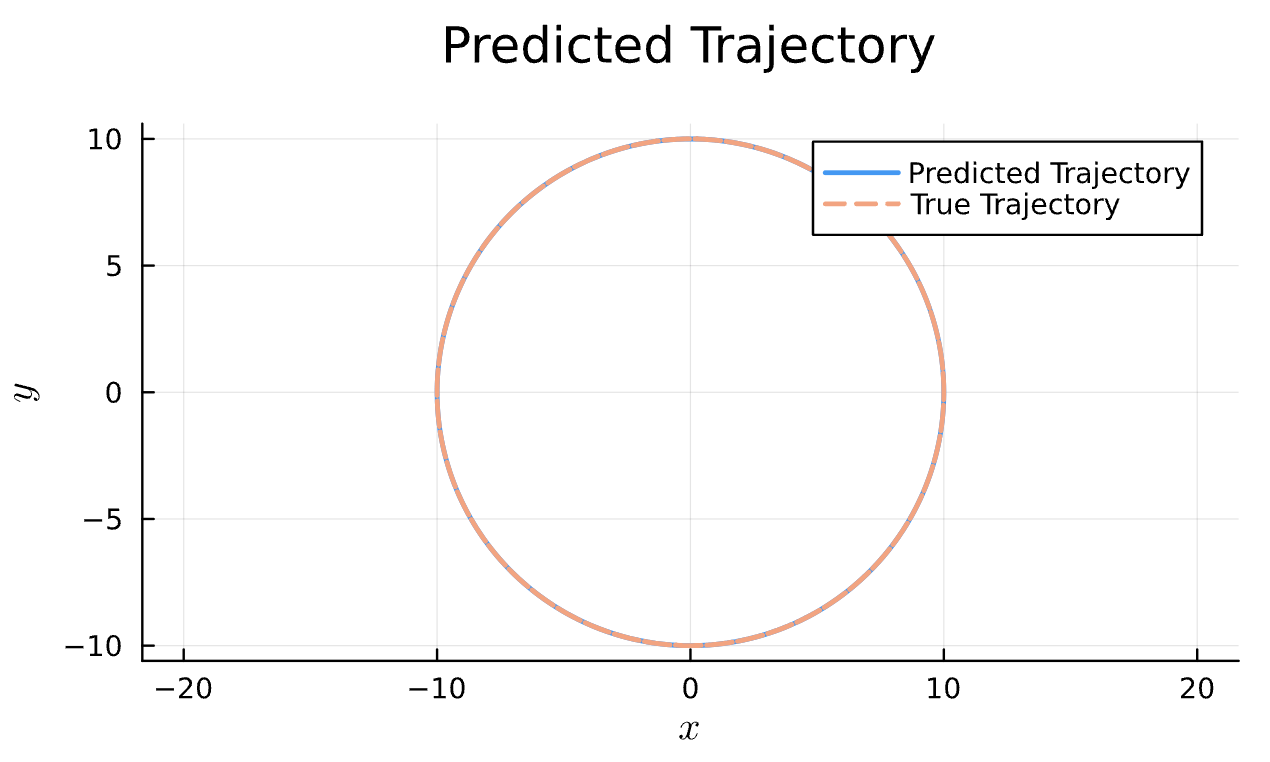
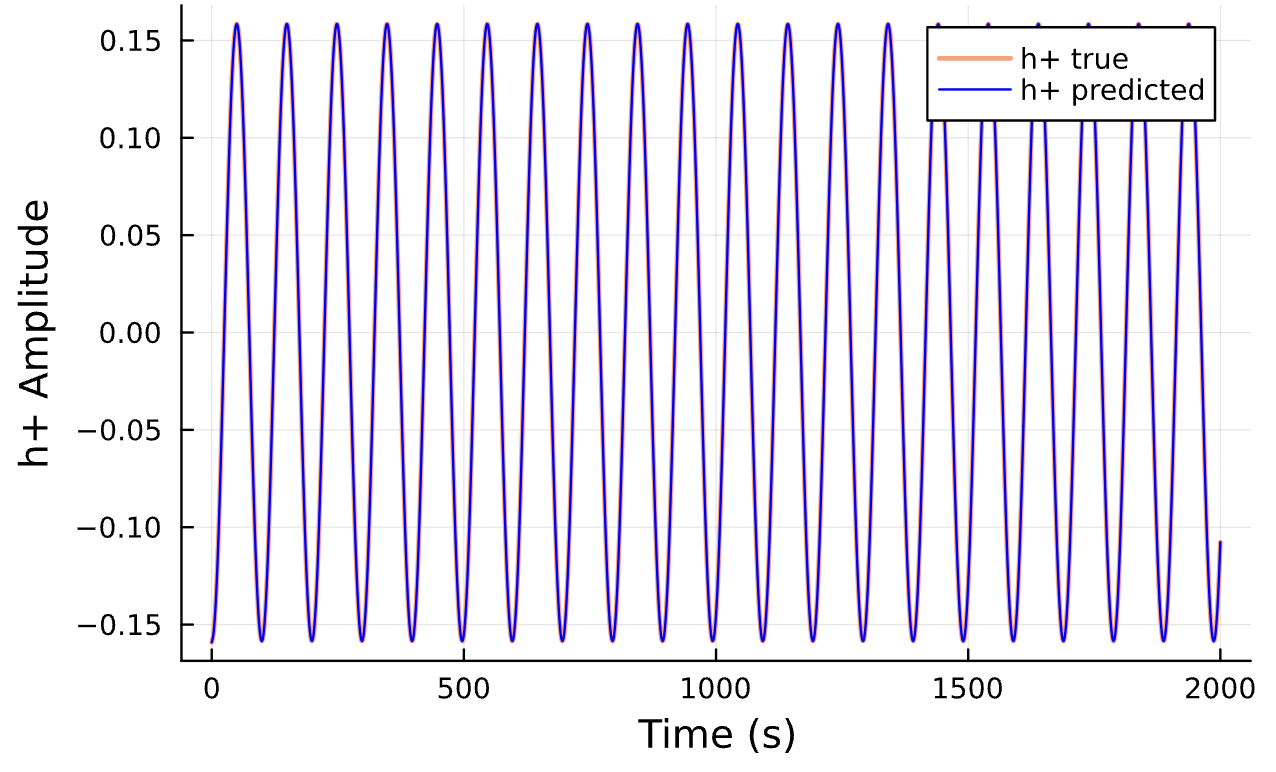
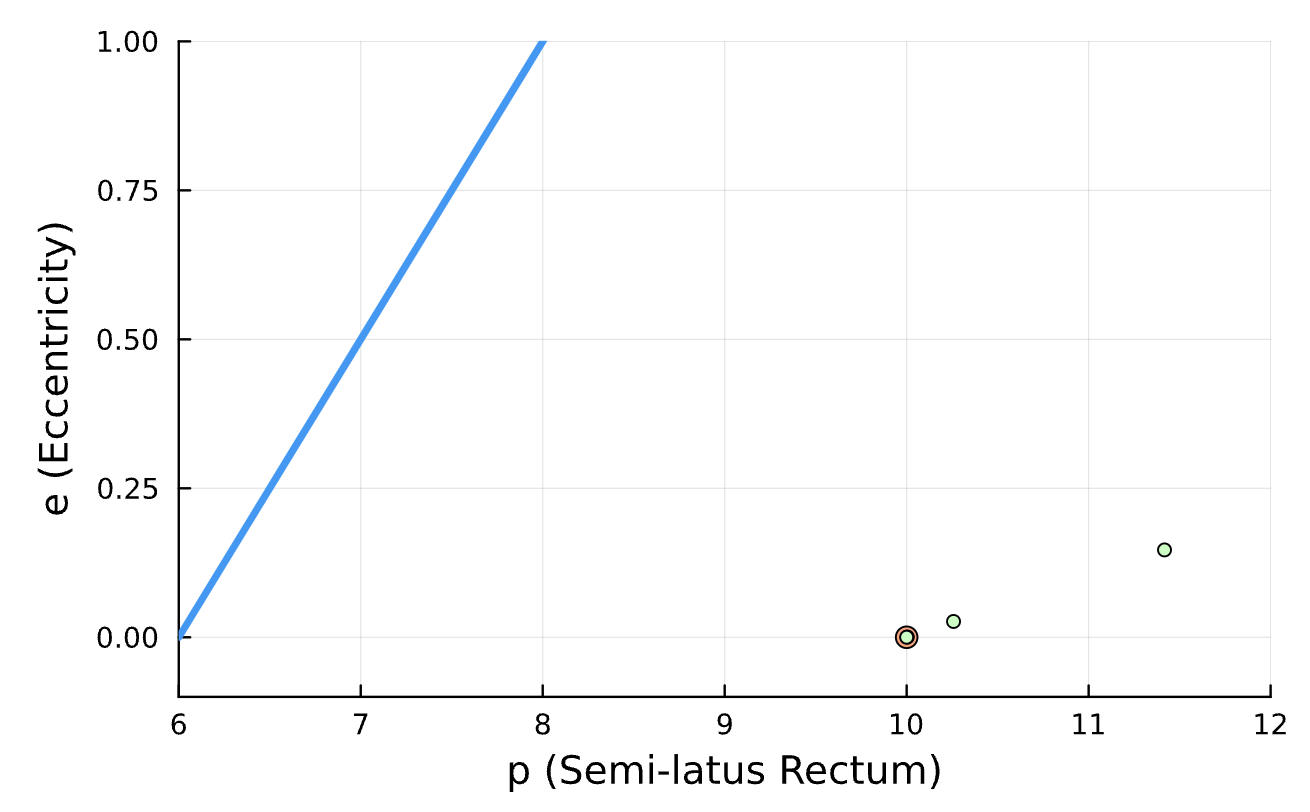
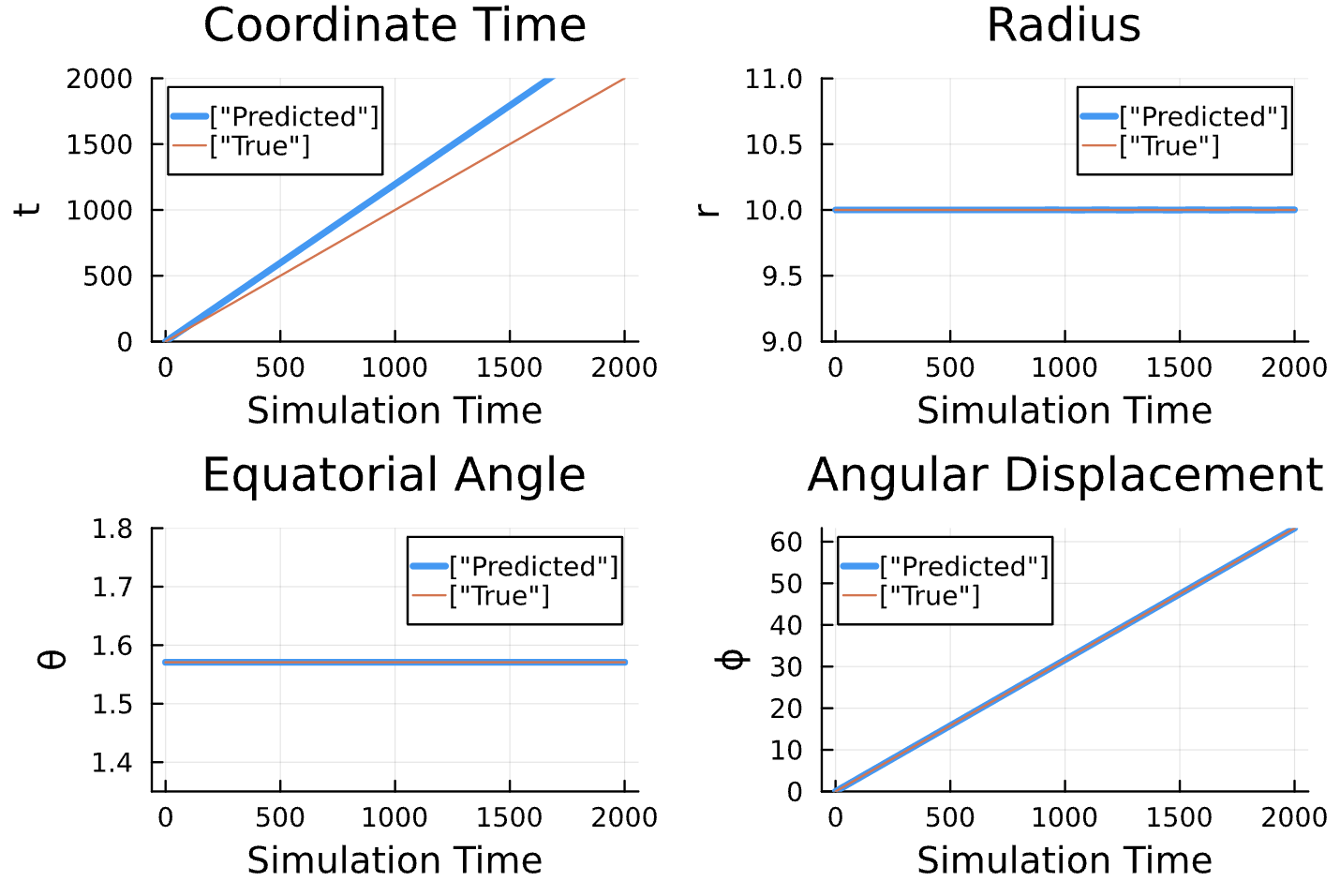
Latest Results

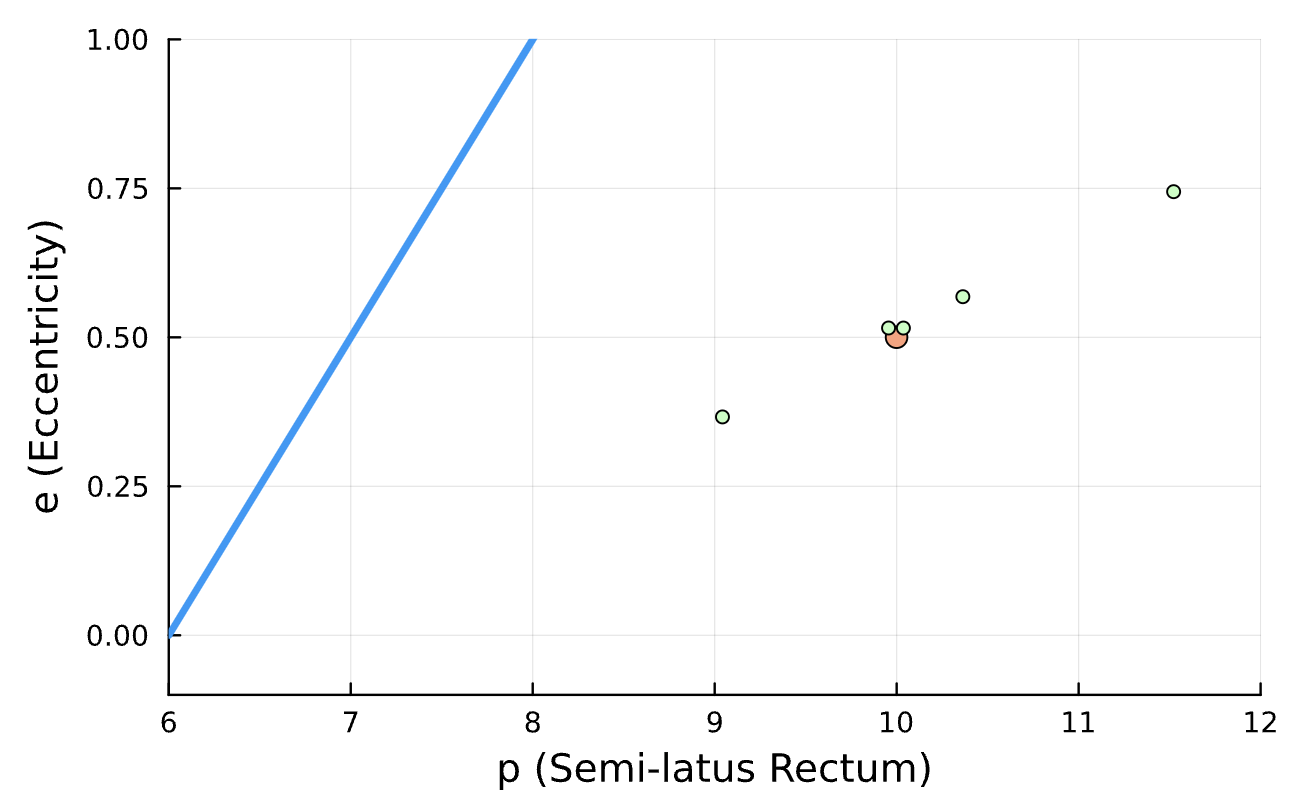
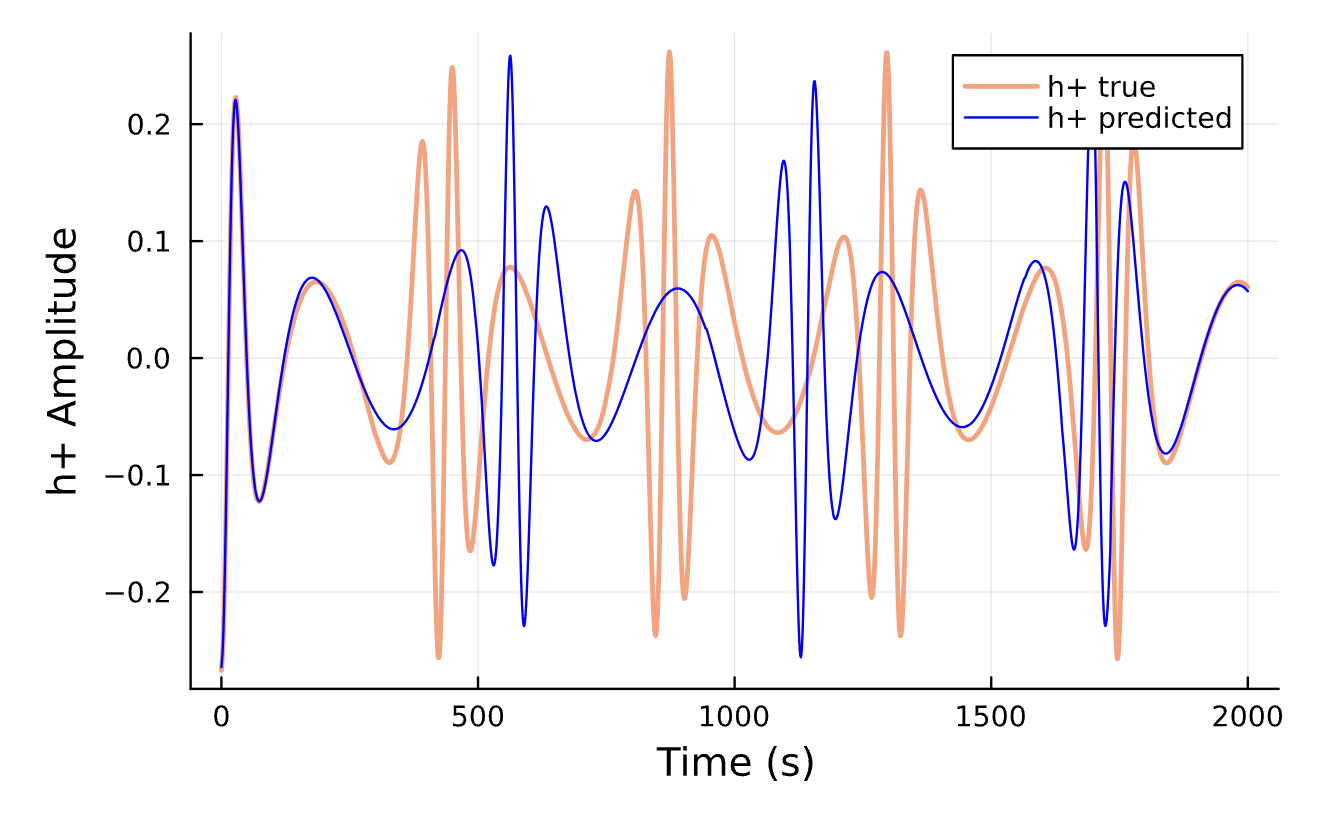
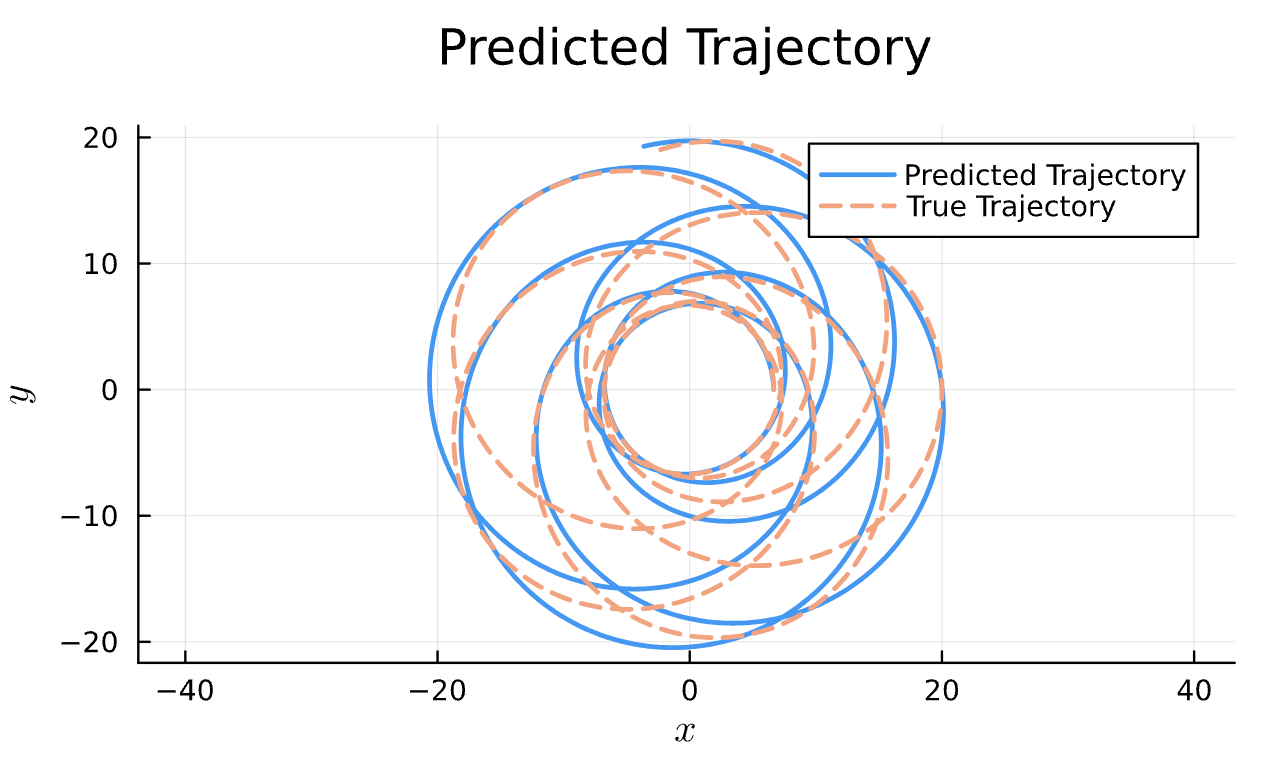
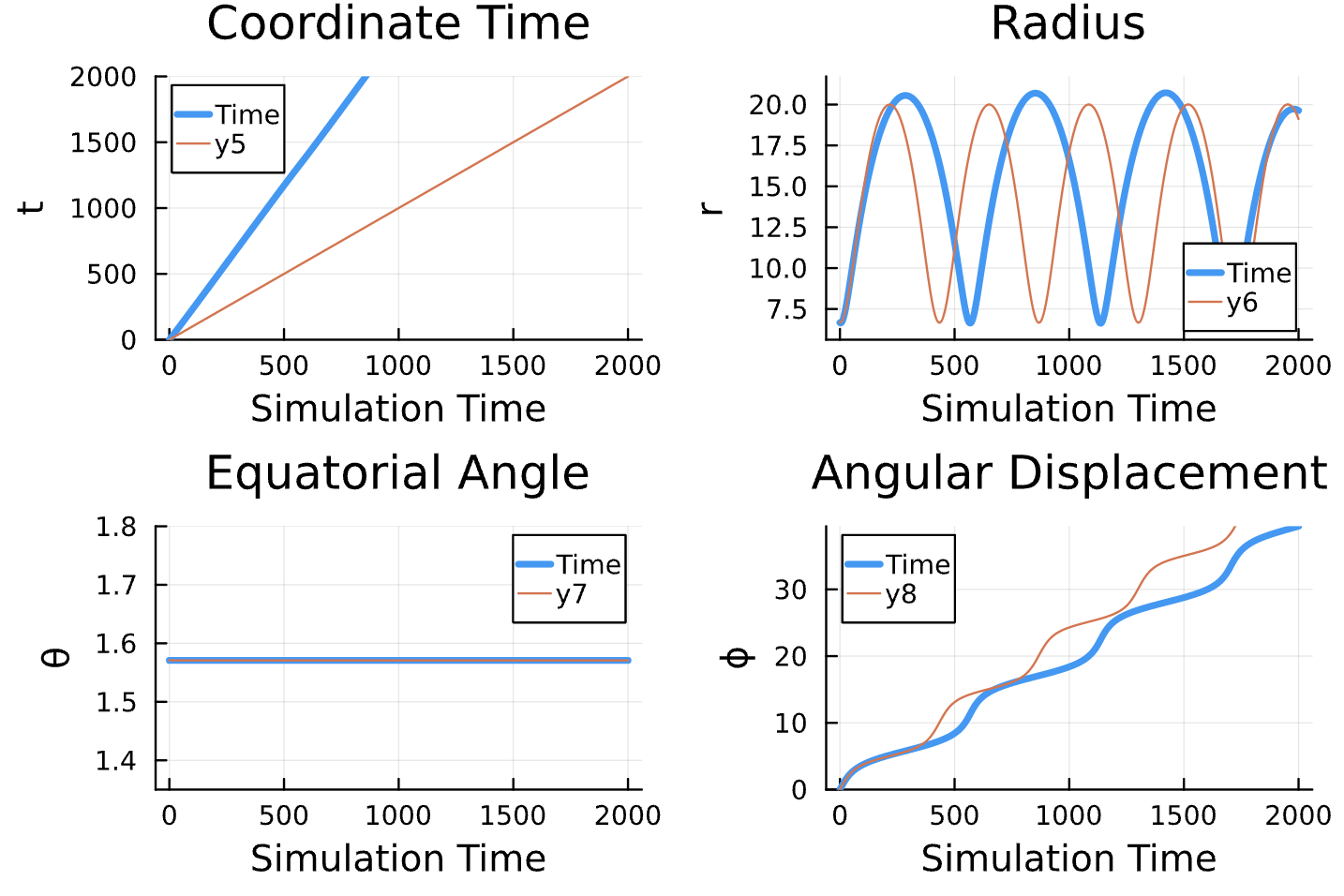
Learning Rate = 7e-3, Epochs = 6, # Iterations = 6, Training = 5% ~ 100/2000 time steps

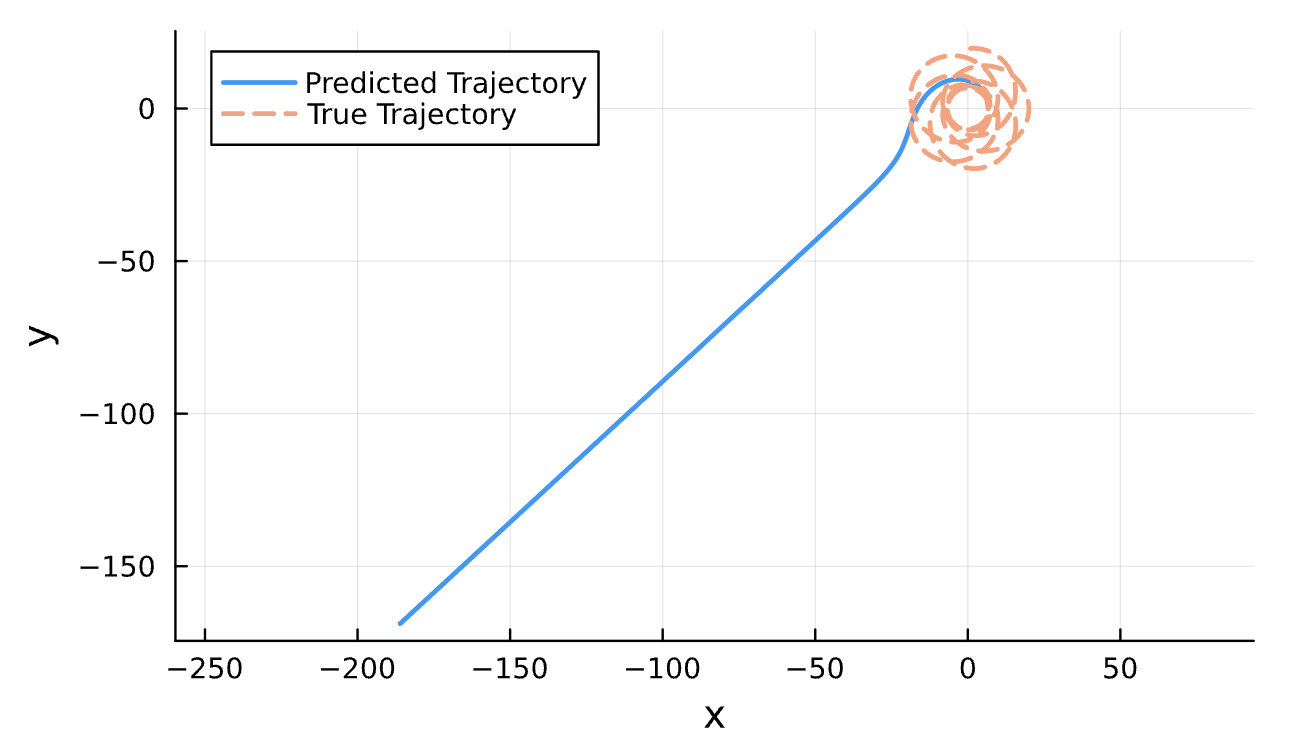
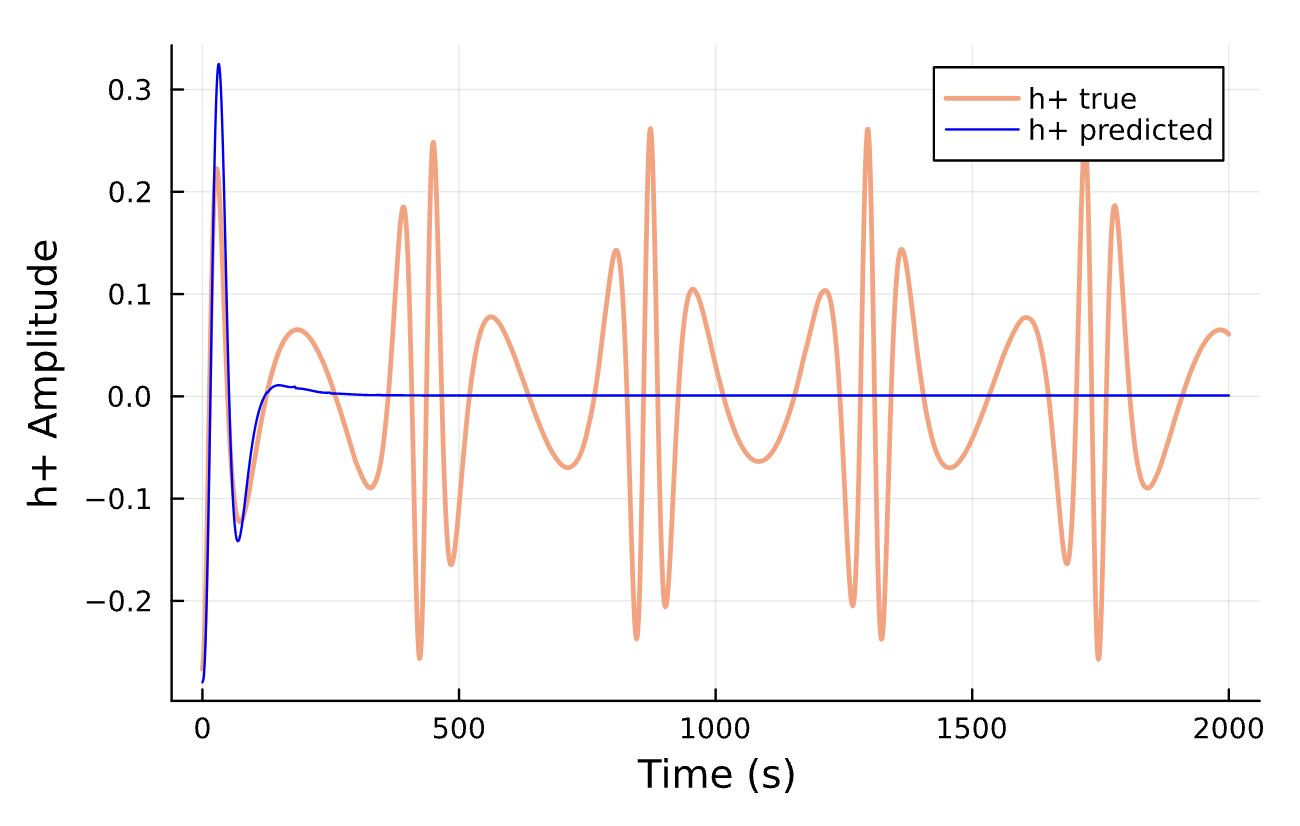
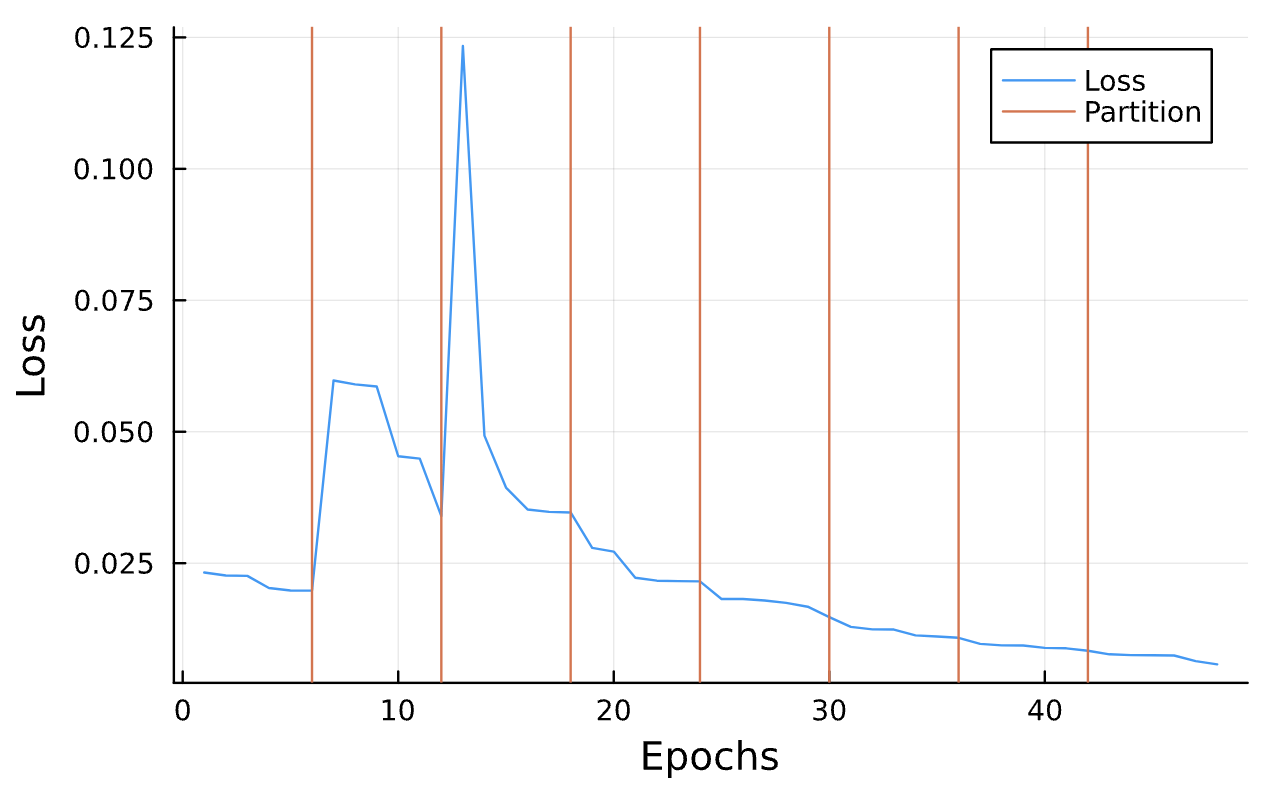
Sensitive!

The Steps

Does the base model even matter?

What are the optimal hyperparameters?

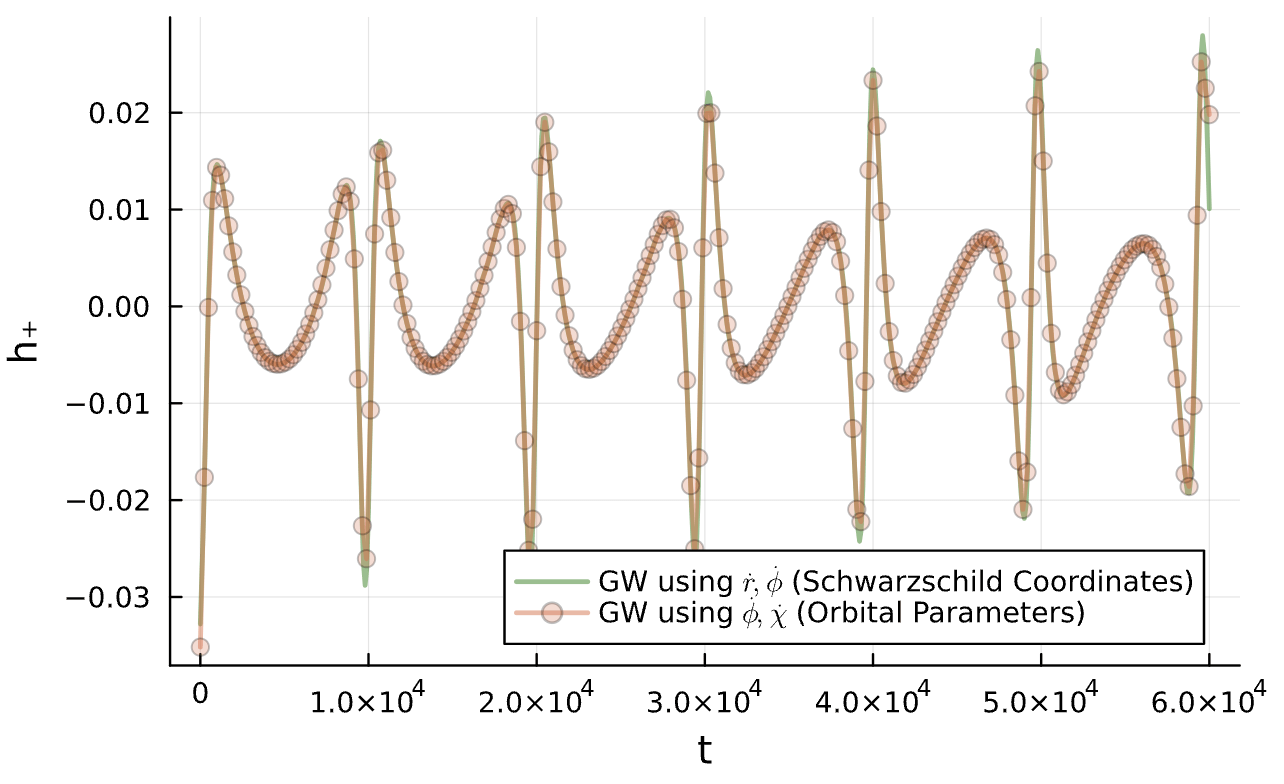
Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

The Steps

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

Yes (thankfully)

Yes (unfortunately)

Yes (no further comment)

Yes (duh)

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
    x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ  
    M, E, L = p
    
    function H(state_vec)
        t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
        f = (1 - ((2*M)/r))

        H_schwarzschild = 1/2 * ( - f^(-1) * (p_t)^2 
								  + f * (p_r)^2 + (p_φ)^2/r^2 )

        return H_schwarzschild
    end
    
    # Compute gradient using ForwardDiff
    grad_H = ForwardDiff.gradient(H, x)

    # Define antisymmetric matrix J (8x8) -- L is taken!
	J = [zeros(4,4)  I(4);
         -I(4)       zeros(4,4)]
    
    # Hamilton's equations: ẋ = J*∇H
    du_dτ = J * grad_H

    t_val, r_val = x[1], x[2]
    f_val = 1 - 2*M/r_val
    dτ_dt = f_val/E

    du .= du_dτ .* dτ_dt
end

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
    x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ  
    M, E, L = p
    
    function H(state_vec)
        t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec

        H_schwarzschild = H(u)

        return H_schwarzschild
    end
    
    # Compute gradient using ForwardDiff
    grad_H = ForwardDiff.gradient(H, x)

    # Define antisymmetric matrix J (8x8)
	J = [zeros(4,4)  I(4);
         -I(4)       zeros(4,4)]
    
    # Hamilton's equations: ẋ = J*∇H
    du_dτ = J * grad_H

    t_val, r_val = x[1], x[2]
    f_val = 1 - 2*M/r_val
    dτ_dt = f_val/E

    du .= du_dτ .* dτ_dt
end

x = \begin{pmatrix} t \\ r \\ \theta \\ \phi \\ p_t \\ p_r \\ p_\theta \\ p_\phi \end{pmatrix}

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
    x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ  
    M, E, L = p
    
    function H(state_vec)
        t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec

        H_schwarzschild = H(u)

        return H_schwarzschild
    end
    
    # Compute gradient using ForwardDiff
    grad_H = ForwardDiff.gradient(H, x)

    # Define antisymmetric matrix J (8x8)
	J = [zeros(4,4)  I(4);
         -I(4)       zeros(4,4)]
    
    # Hamilton's equations: ẋ = J*∇H
    du_dτ = J * grad_H

    t_val, r_val = x[1], x[2]
    f_val = 1 - 2*M/r_val
    dτ_dt = f_val/E

    du .= du_dτ .* dτ_dt
end

\begin{align*}H_{S} = & - \left(1-\frac{2M}{r}\right)^{-1}\frac{p_t^2}{2} \\ &+ \left(1-\frac{2M}{r}\right) \frac{p_r^2}{2} \\ &+ \frac{p_φ^2}{2r^2}\end{align*}

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
    x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ  
    M, E, L = p
    
    function H(state_vec)
        t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec

        H_schwarzschild = H(u)

        return H_schwarzschild
    end
    
    # Compute gradient using ForwardDiff
    grad_H = ForwardDiff.gradient(H, x)

    # Define antisymmetric matrix J (8x8)
	J = [zeros(4,4)  I(4);
         -I(4)       zeros(4,4)]
    
    # Hamilton's equations: ẋ = J*∇H
    du_dτ = J * grad_H

    t_val, r_val = x[1], x[2]
    f_val = 1 - 2*M/r_val
    dτ_dt = f_val/E

    du .= du_dτ .* dτ_dt
end

\nabla H

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

J=\begin{pmatrix} 0 & I \\ -I & 0\end{pmatrix}

function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
    x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ  
    M, E, L = p
    
    function H(state_vec)
        t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec

        H_schwarzschild = H(u)

        return H_schwarzschild
    end
    
    # Compute gradient using ForwardDiff
    grad_H = ForwardDiff.gradient(H, x)

    # Define antisymmetric matrix J (8x8)
	J = [zeros(4,4)  I(4);
         -I(4)       zeros(4,4)]
    
    # Hamilton's equations: ẋ = J*∇H
    du_dτ = J * grad_H

    t_val, r_val = x[1], x[2]
    f_val = 1 - 2*M/r_val
    dτ_dt = f_val/E

    du .= du_dτ .* dτ_dt
end

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

\dot{x} = J\nabla H

function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
    x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ  
    M, E, L = p
    
    function H(state_vec)
        t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec

        H_schwarzschild = H(u)

        return H_schwarzschild
    end
    
    # Compute gradient using ForwardDiff
    grad_H = ForwardDiff.gradient(H, x)

    # Define antisymmetric matrix J (8x8)
	J = [zeros(4,4)  I(4);
         -I(4)       zeros(4,4)]
    
    # Hamilton's equations: ẋ = J*∇H
    du_dτ = J * grad_H

    t_val, r_val = x[1], x[2]
    f_val = 1 - 2*M/r_val
    dτ_dt = f_val/E

    du .= du_dτ .* dτ_dt
end

\dot{x} = \frac{dx}{d\tau} \to x(\tau)

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
    x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ  
    M, E, L = p
    
    function H(state_vec)
        t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec

        H_schwarzschild = H(u)

        return H_schwarzschild
    end
    
    # Compute gradient using ForwardDiff
    grad_H = ForwardDiff.gradient(H, x)

    # Define antisymmetric matrix J (8x8)
	J = [zeros(4,4)  I(4);
         -I(4)       zeros(4,4)]
    
    # Hamilton's equations: ẋ = J*∇H
    du_dτ = J * grad_H

    t_val, r_val = x[1], x[2]
    f_val = 1 - 2*M/r_val
    dτ_dt = f_val/E

    du .= du_dτ .* dτ_dt
end

\frac{dx}{dt} = \frac{dx}{d\tau}\frac{d\tau}{dt}

\frac{d\tau}{dt}=\left( \frac{dt}{d\tau}\right)^{-1}=\left(\frac{E}{1-\frac{2M}{r}}\right)^{-1}

The Steps

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

    function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
        x = u
        NN_params = p.NN
        M, E, L = p.parameters.M, p.parameters.E, p.parameters.L

        function H(state_vec)
            define state_vector
            define H_kepler
            define NN_correction
            return H_kepler + NN_correction
        end
        
        # Compute gradient using ForwardDiff
        grad_H = ForwardDiff.gradient(H, x)
        
        # Define symplectic matrix L (8x8)
        J = [zeros(4,4)  I(4);
             -I(4)       zeros(4,4)]
        
        # Hamilton's equations: ẋ = J*∇H
        du_dτ = J * grad_H

        t_val, r_val = x[1], x[2]
        f_val = 1 - 2*M/r_val
        dτ_dt = f_val/E
        
        du .= du_dτ .* dτ_dt

    end

\dot{x}(\tau) \to \dot{x}(t)

The Steps

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

using hyperopt

function objective_function(lr, epochs, numCycles, train%)
  parameter_error = optimizeBlackHole(learningRate = learningRate,
                                      epochsPerIteration = epochsPerIteration, 
                                      numberOfCycles = numberOfCycles,
                                      totalTrainingPercent = totalTrainingPercent,
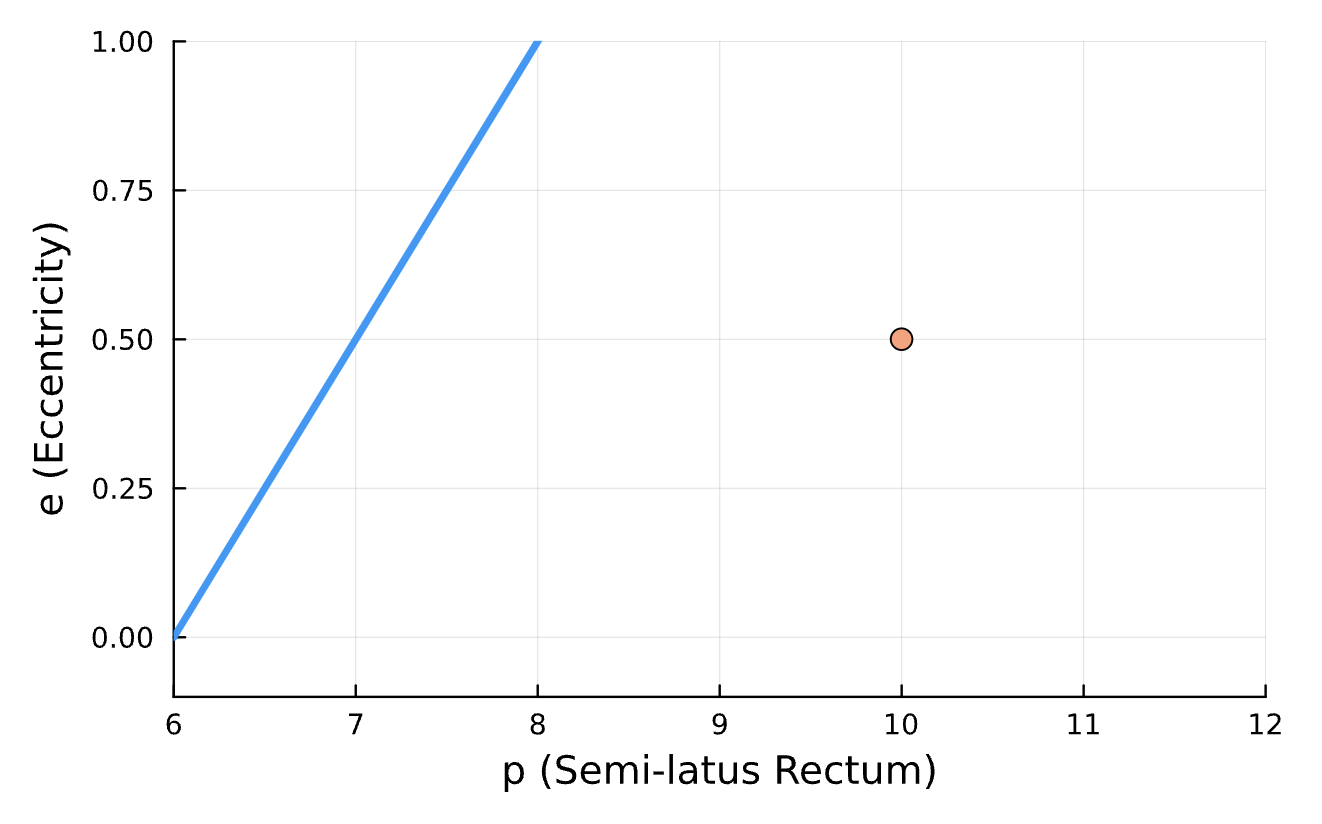
                                      true_parameters = [10, 0.2],
                                      initial_guess = [10, 0.2])
  println("lr=$learningRate, epochs=$epochsPerIteration → error=$parameter_error")
  return parameter_error
end

ho = @hyperopt for i=20,
    learningRate = [1e-3, 3e-3, 6e-3, 1e-2, 2e-2], 
    epochsPerIteration = [2, 5, 10, 20, 50],      
    numberOfCycles = [3, 5, 7, 10, 15],            
    totalTrainingPercent = [0.1, 0.2, 0.3, 0.5, 0.7]  
    
    objective_function(learningRate, epochsPerIteration, 
					   numberOfCycles, totalTrainingPercent)
end

Learning Rate = 6e-3, Epochs = 10

# Iterations = 15, Training = 20%

Base Model

Does the base model even matter?

What are the optimal hyperparameters?

Do we have to be careful with proper v. coordinate time?

Does my training data match the 2021 paper's training data?

H_{Kepler} = 0

H_{Kepler} = \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2}

H_{Kepler} = \frac{p_r^2}{2}

H_{Kepler} = \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2} - \frac{M}{r}

complexity

Base Model

Does the base model even matter?

H_{Kepler} = 0

H_{Kepler} = \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2}

H_{Kepler} = \frac{p_r^2}{2}

H_{Kepler} = \frac{p_r^2}{2} + \frac{p_φ^2}{2r^2} - \frac{M}{r}

complexity