Binary Black Holes
A GENERIC Approach
Ref Bari
Advisor: Prof. Brendan Keith



Goal
Neural ODE

Goal
Neural ODE:
Training Data
Goal
Neural ODE:
Training Data

Goal
Neural ODE:
Training Data

Goal
Neural ODE:
Training Data
ODE Solver:

Goal
Neural ODE:
Training Data
ODE Solver:


Neural ODE:
Training Data
ODE Solver:
BFGS Optimizer:
Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:

Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_kepler = p_r^2/2 - M/r + p_φ^2/(2*r^2) + p_t
NN_correction = NN([r, p_r, p_φ, p_t], NN_params, NN_state)[1][1]
return H_kepler + NN_correction
end
# Compute gradient of Hamiltonian
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix L
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
dH_dpₜ = grad_H[5]
dτ_dt = (dH_dpₜ)^(-1)
du .= du_dτ .* dτ_dt
du[1] = 1
end
Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_kepler = p_r^2/2 - M/r + p_φ^2/(2*r^2) + p_t
NN_correction = NN([r, p_r, p_φ, p_t], NN_params, NN_state)[1][1]
return H_kepler + NN_correction
end
# Compute gradient of Hamiltonian
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix L
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
dH_dpₜ = grad_H[5]
dτ_dt = (dH_dpₜ)^(-1)
du .= du_dτ .* dτ_dt
du[1] = 1
end
Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_kepler = p_r^2/2 - M/r + p_φ^2/(2*r^2) + p_t
NN_correction = NN([r, p_r, p_φ, p_t], NN_params, NN_state)[1][1]
return H_kepler + NN_correction
end
# Compute gradient of Hamiltonian
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix L
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
dH_dpₜ = grad_H[5]
dτ_dt = (dH_dpₜ)^(-1)
du .= du_dτ .* dτ_dt
du[1] = 1
end
Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_kepler = p_r^2/2 - M/r + p_φ^2/(2*r^2) + p_t
NN_correction = NN([r, p_r, p_φ, p_t], NN_params, NN_state)[1][1]
return H_kepler + NN_correction
end
# Compute gradient of Hamiltonian
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix L
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
dH_dpₜ = grad_H[5]
dτ_dt = (dH_dpₜ)^(-1)
du .= du_dτ .* dτ_dt
du[1] = 1
end
Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_kepler = p_r^2/2 - M/r + p_φ^2/(2*r^2) + p_t
NN_correction = NN([r, p_r, p_φ, p_t], NN_params, NN_state)[1][1]
return H_kepler + NN_correction
end
# Compute gradient of Hamiltonian
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix L
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
dH_dpₜ = grad_H[5]
dτ_dt = (dH_dpₜ)^(-1)
du .= du_dτ .* dτ_dt
du[1] = 1
end
Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_kepler = p_r^2/2 - M/r + p_φ^2/(2*r^2) + p_t
NN_correction = NN([r, p_r, p_φ, p_t], NN_params, NN_state)[1][1]
return H_kepler + NN_correction
end
# Compute gradient of Hamiltonian
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix L
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
dH_dpₜ = grad_H[5]
dτ_dt = (dH_dpₜ)^(-1)
du .= du_dτ .* dτ_dt
du[1] = 1
end
Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_kepler = p_r^2/2 - M/r + p_φ^2/(2*r^2) + p_t
NN_correction = NN([r, p_r, p_φ, p_t], NN_params, NN_state)[1][1]
return H_kepler + NN_correction
end
# Compute gradient of Hamiltonian
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix L
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
dH_dpₜ = grad_H[5]
dτ_dt = (dH_dpₜ)^(-1)
du .= du_dτ .* dτ_dt
du[1] = 1
end
Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_kepler = p_r^2/2 - M/r + p_φ^2/(2*r^2) + p_t
NN_correction = NN([r, p_r, p_φ, p_t], NN_params, NN_state)[1][1]
return H_kepler + NN_correction
end
# Compute gradient of Hamiltonian
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix L
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
dH_dpₜ = grad_H[5]
dτ_dt = (dH_dpₜ)^(-1)
du .= du_dτ .* dτ_dt
du[1] = 1
end
Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_kepler = p_r^2/2 - M/r + p_φ^2/(2*r^2) + p_t
NN_correction = NN([r, p_r, p_φ, p_t], NN_params, NN_state)[1][1]
return H_kepler + NN_correction
end
# Compute gradient of Hamiltonian
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix L
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
# Convert to Coordinate Time!
dH_dpₜ = grad_H[5]
dτ_dt = (dH_dpₜ)^(-1)
du .= du_dτ .* dτ_dt
du[1] = 1
end
Neural ODE:
Training Data:
ODE Solver:
BFGS Optimizer:
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_kepler = p_r^2/2 - M/r + p_φ^2/(2*r^2) + p_t
NN_correction = NN([r, p_r, p_φ, p_t], NN_params, NN_state)[1][1]
return H_kepler + NN_correction
end
# Compute gradient of Hamiltonian
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix L
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
# Convert to Coordinate Time!
dH_dpₜ = grad_H[5]
dτ_dt = (dH_dpₜ)^(-1)
du .= du_dτ .* dτ_dt
du[1] = 1
end
Results
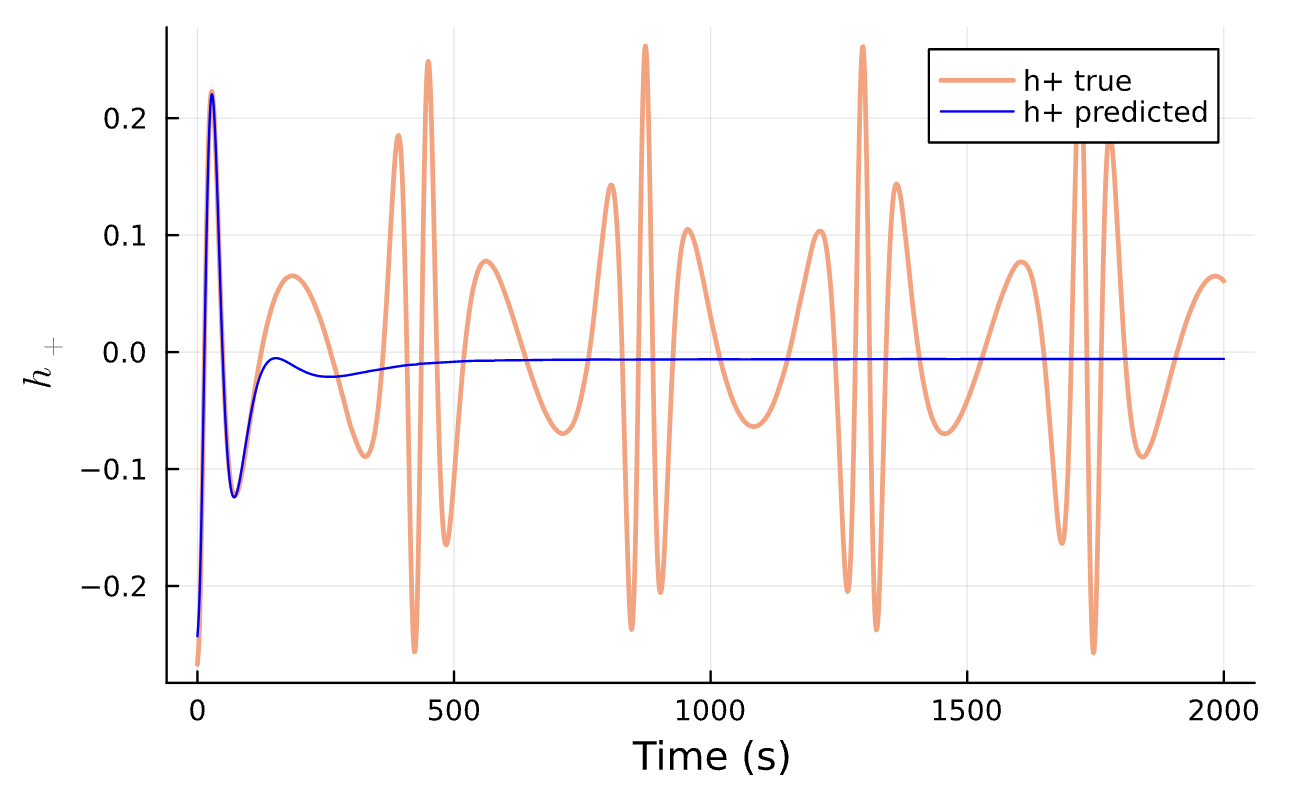

Results


Results


Results

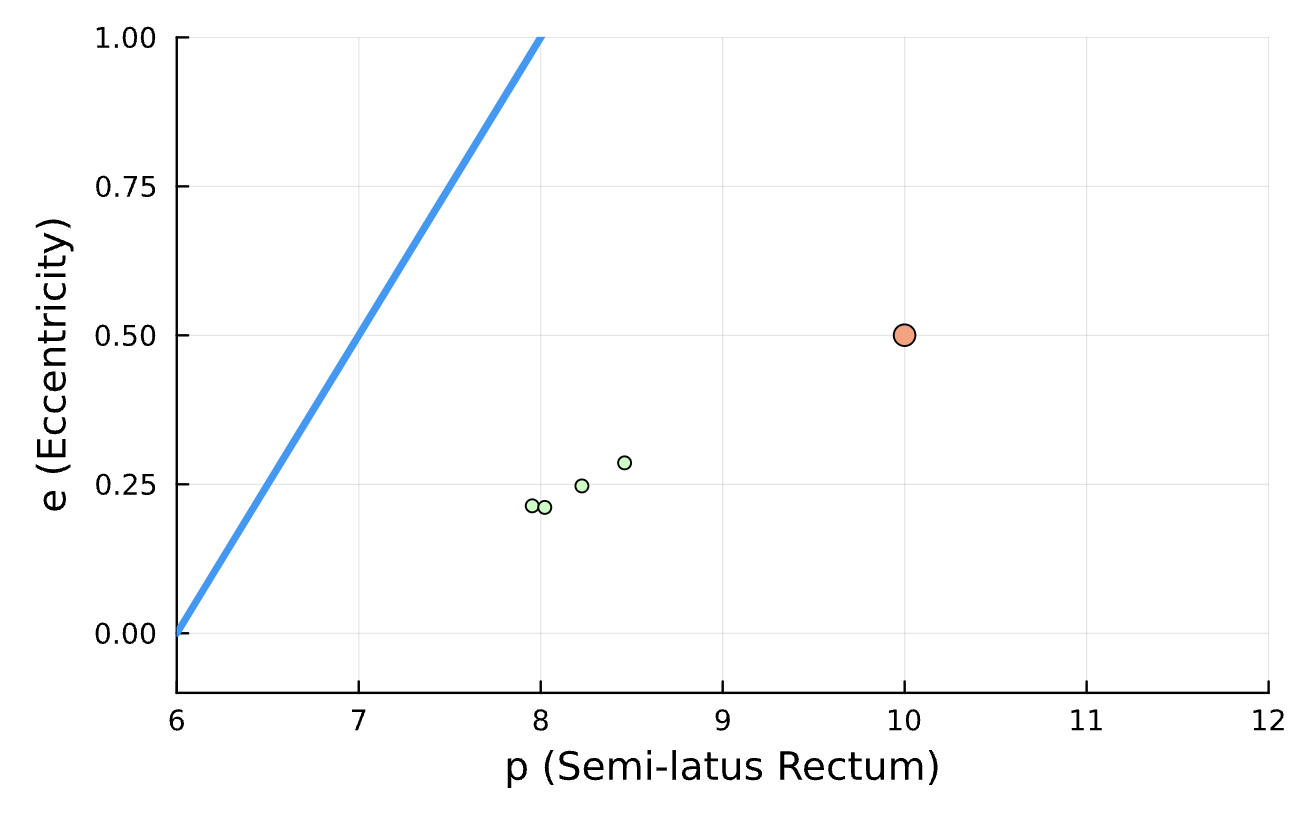
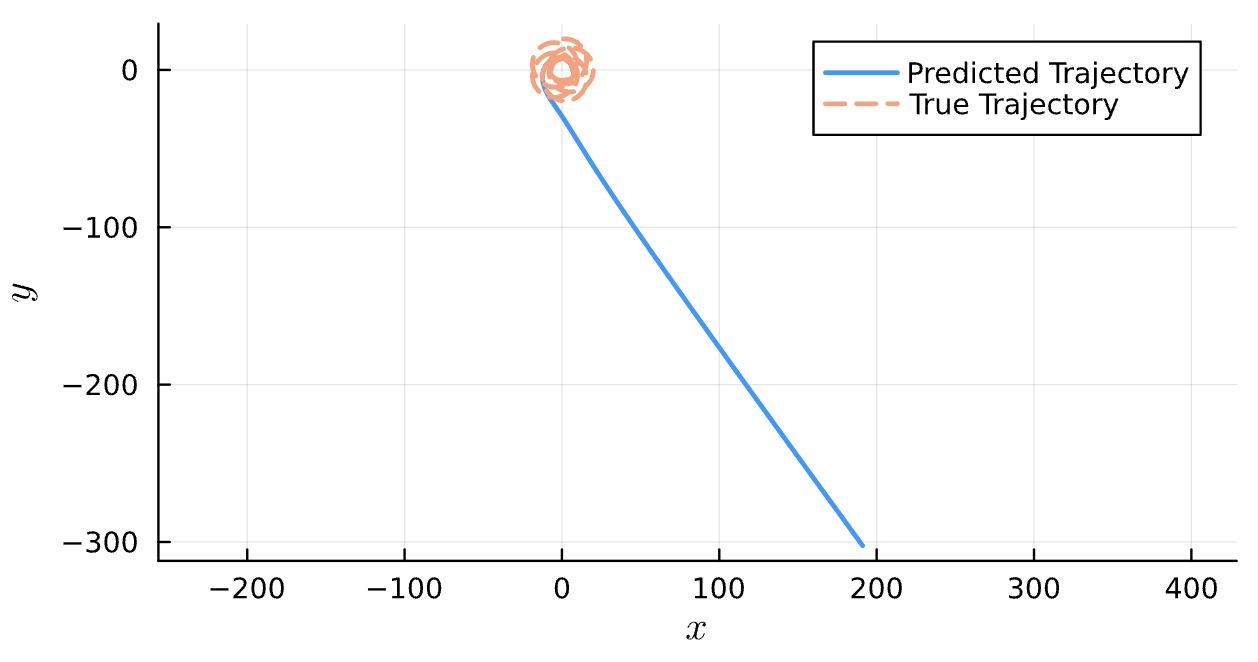
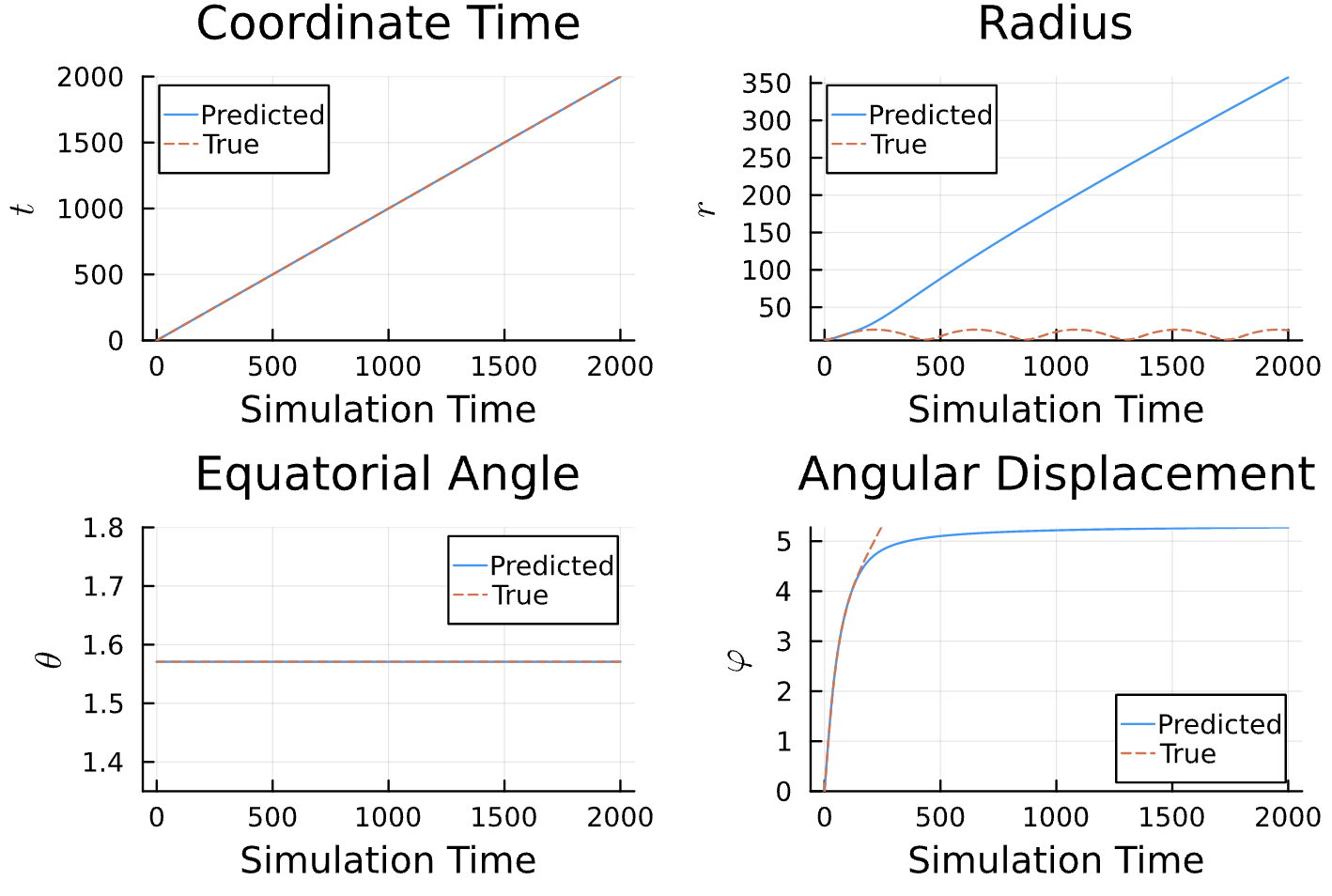
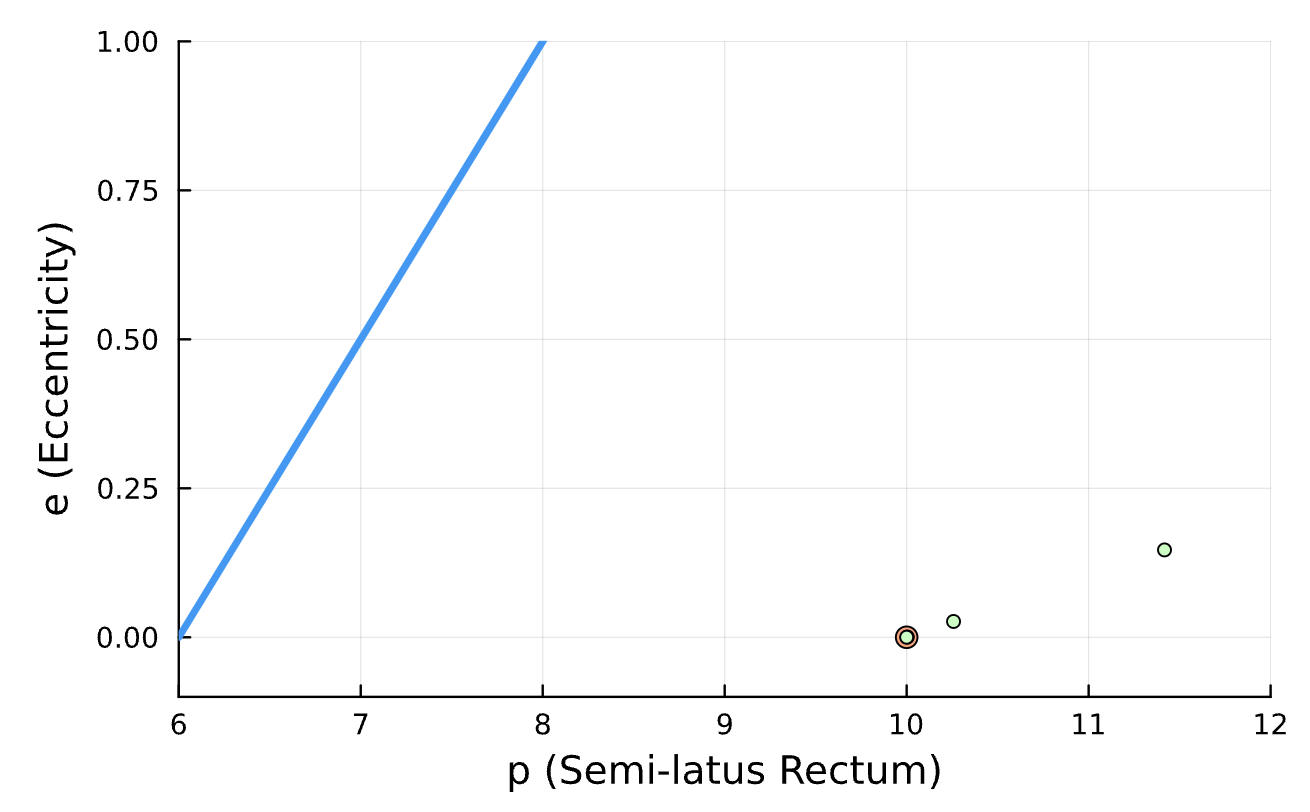
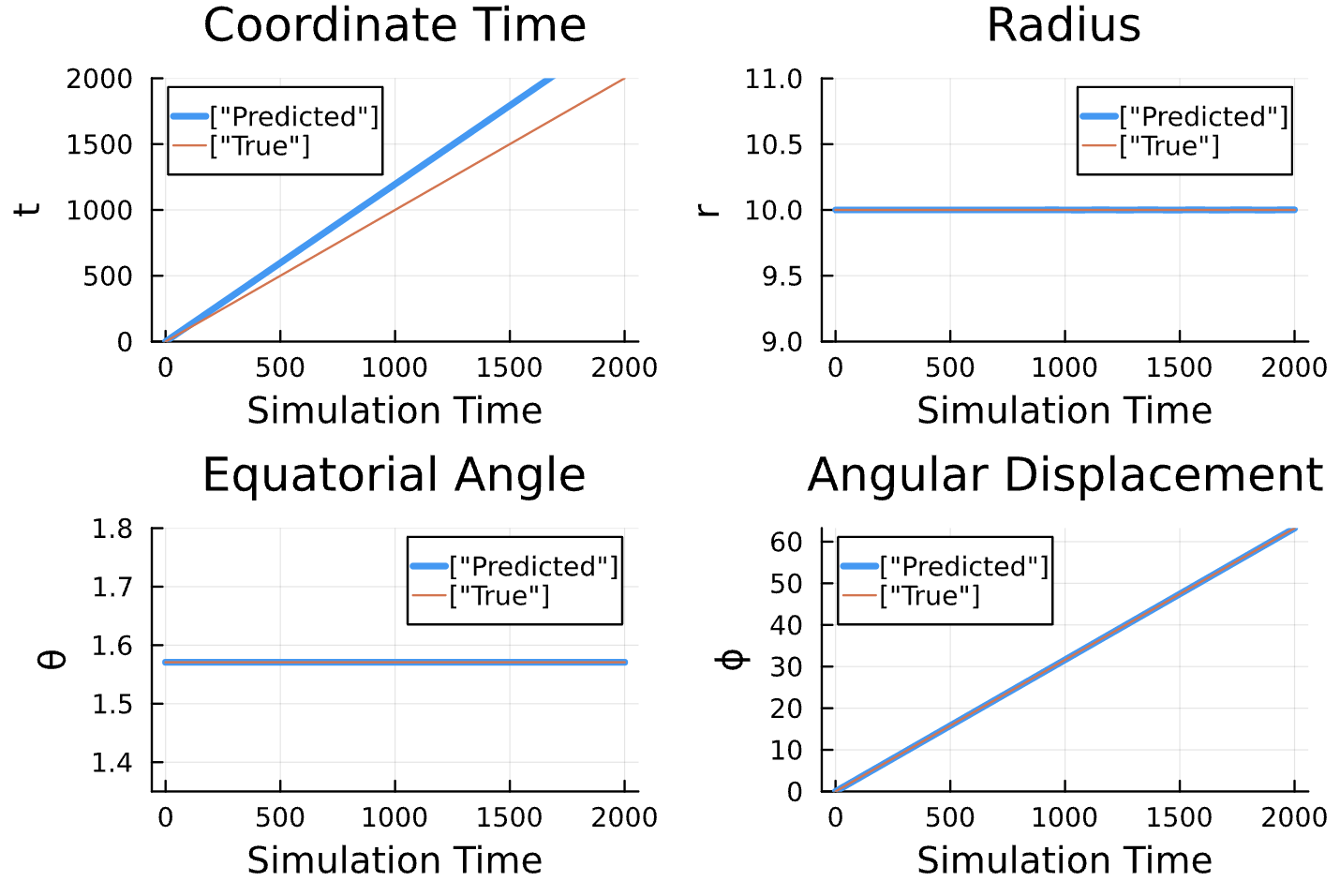
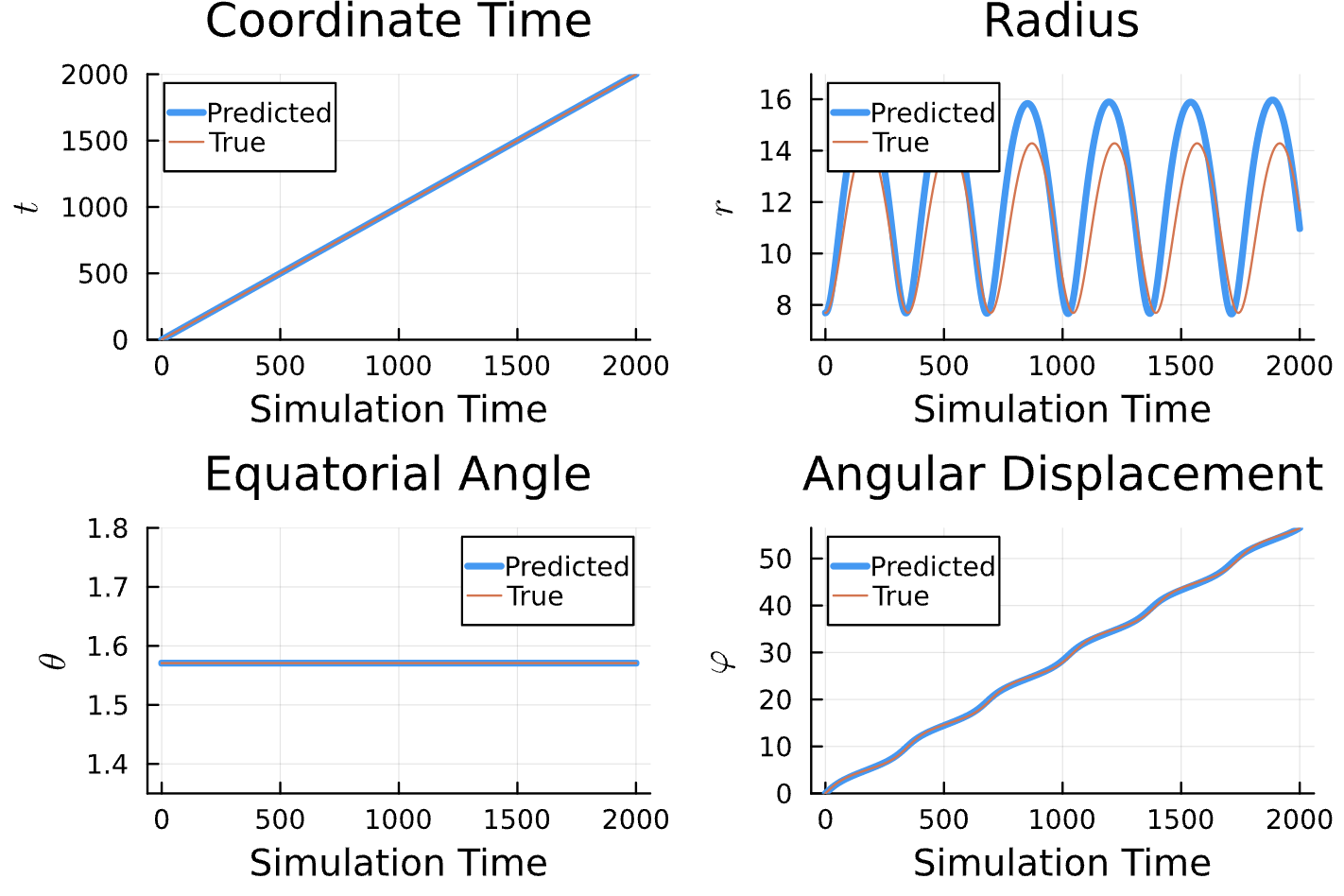
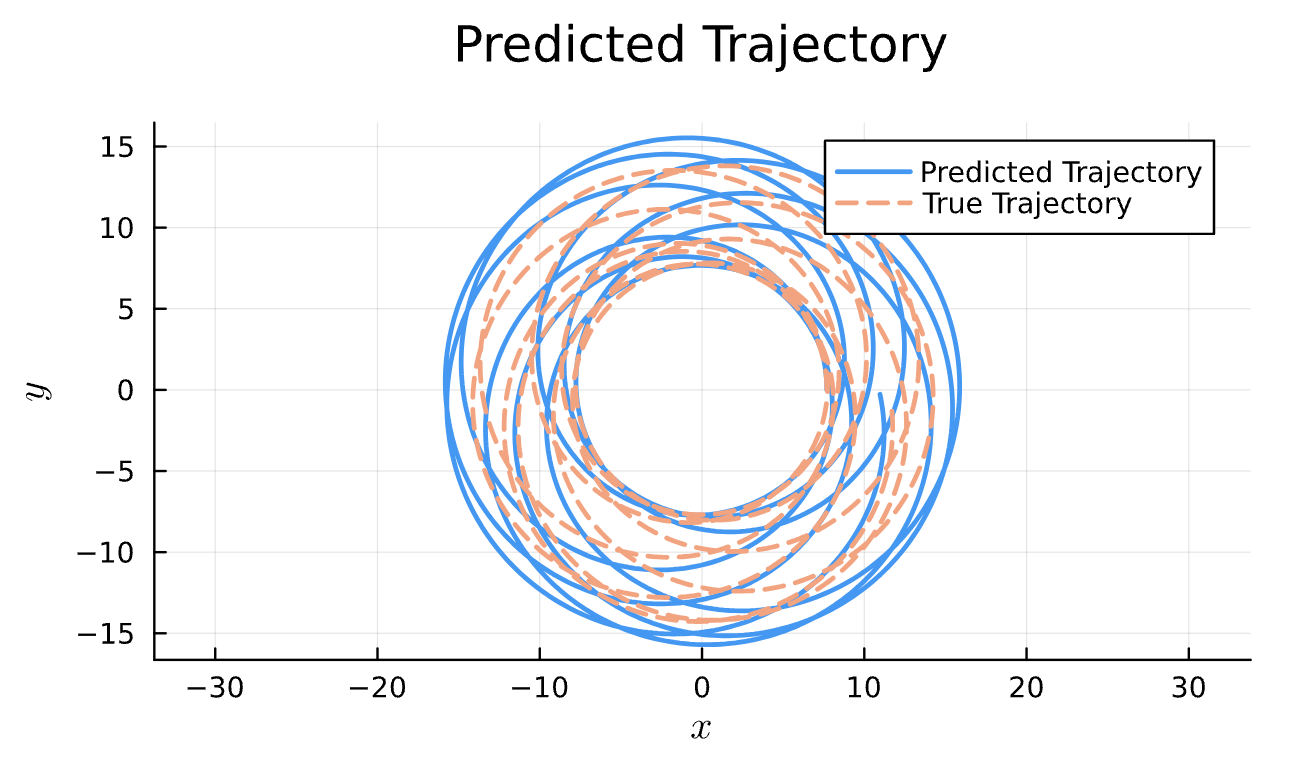
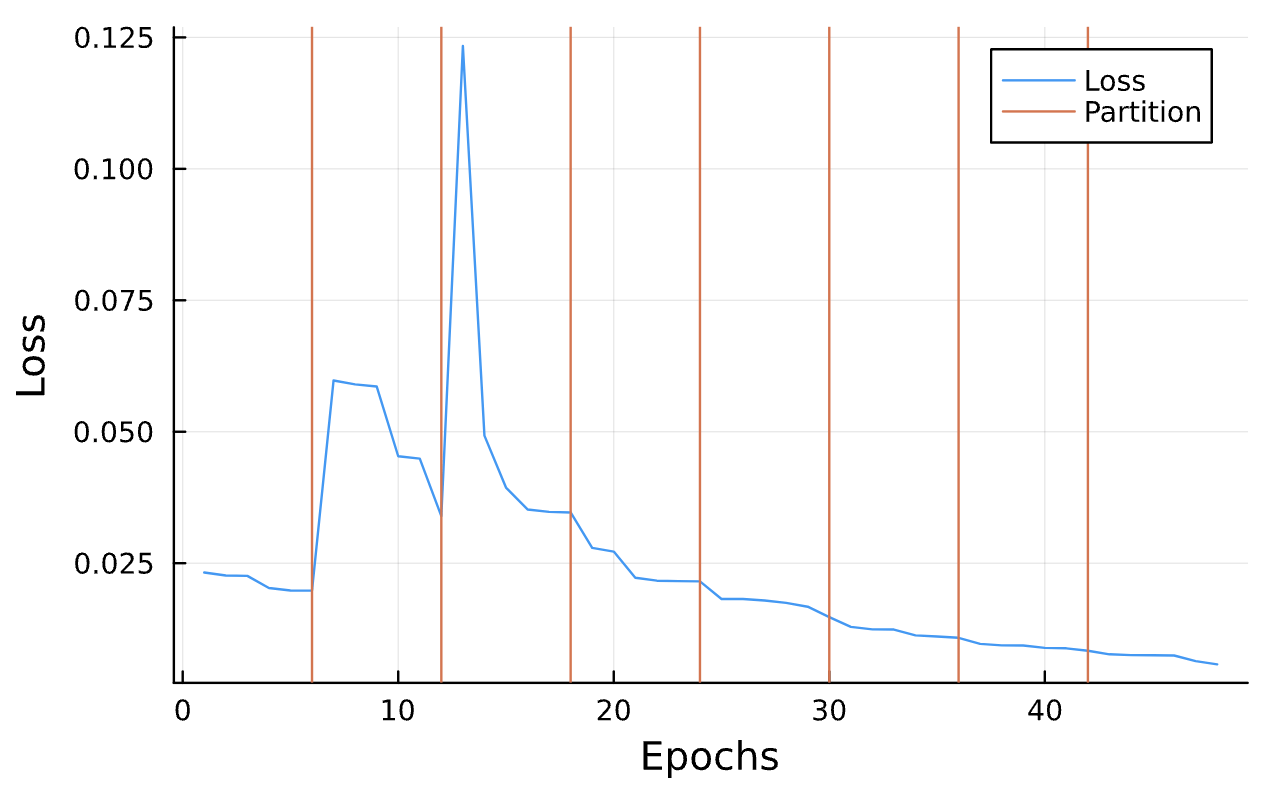
Learning Rate = 1e-2, Epochs = 5, # Iterations = 7, Training = 5% ~ 100/2000 time steps
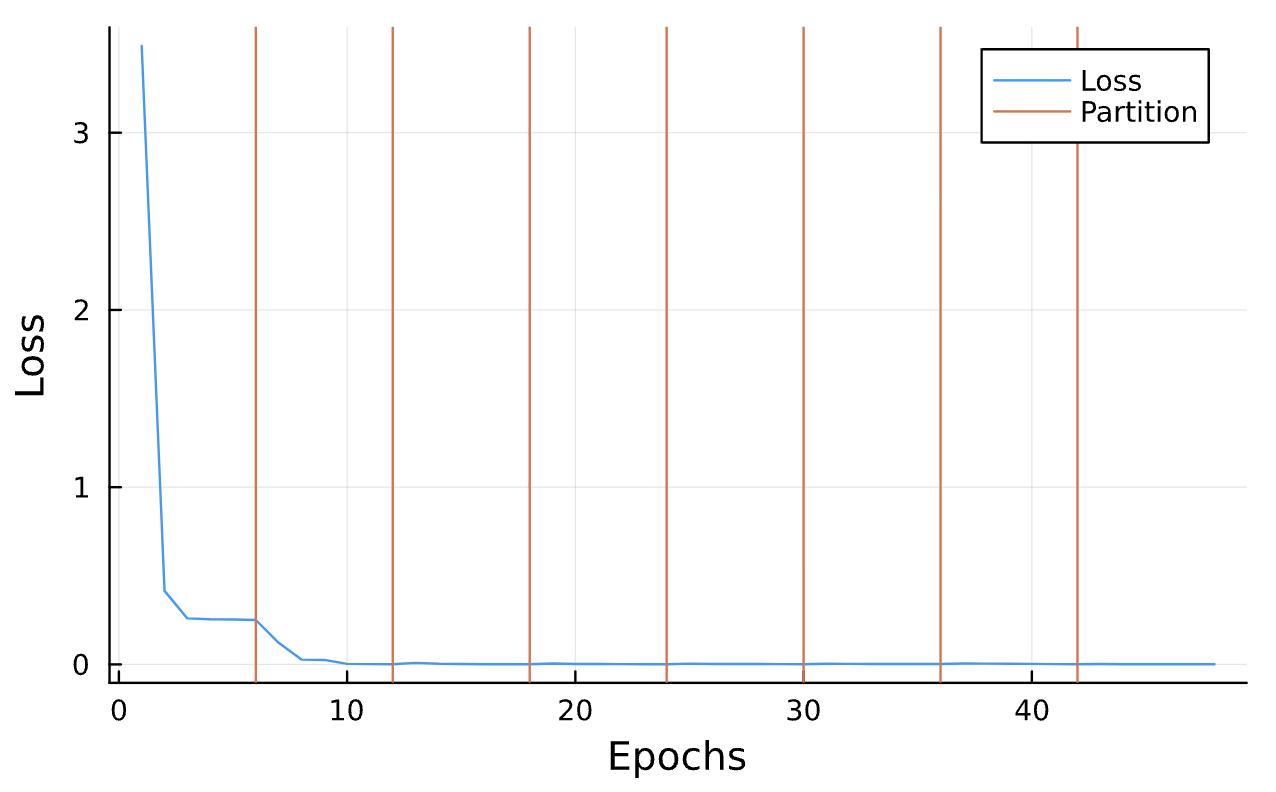
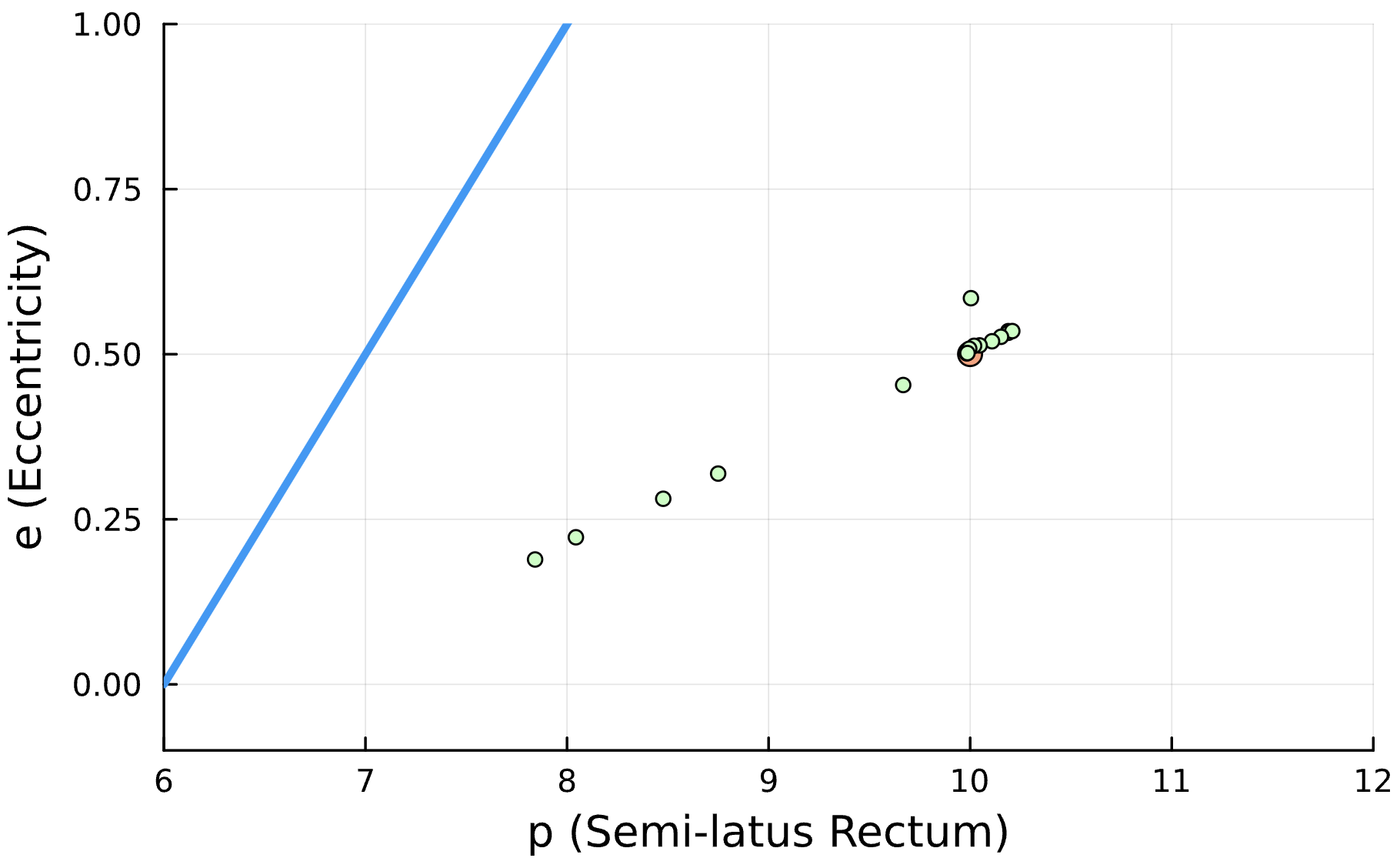
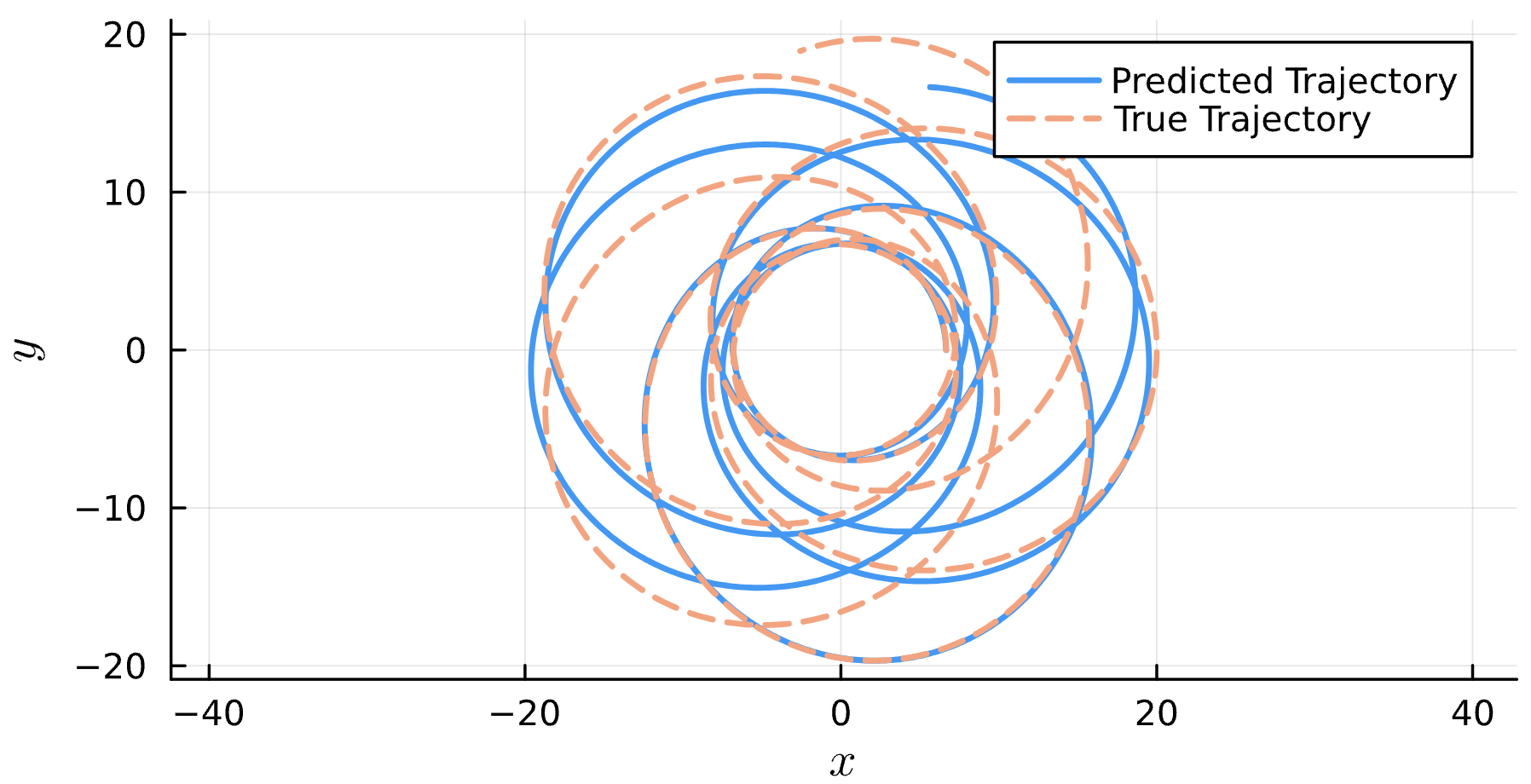
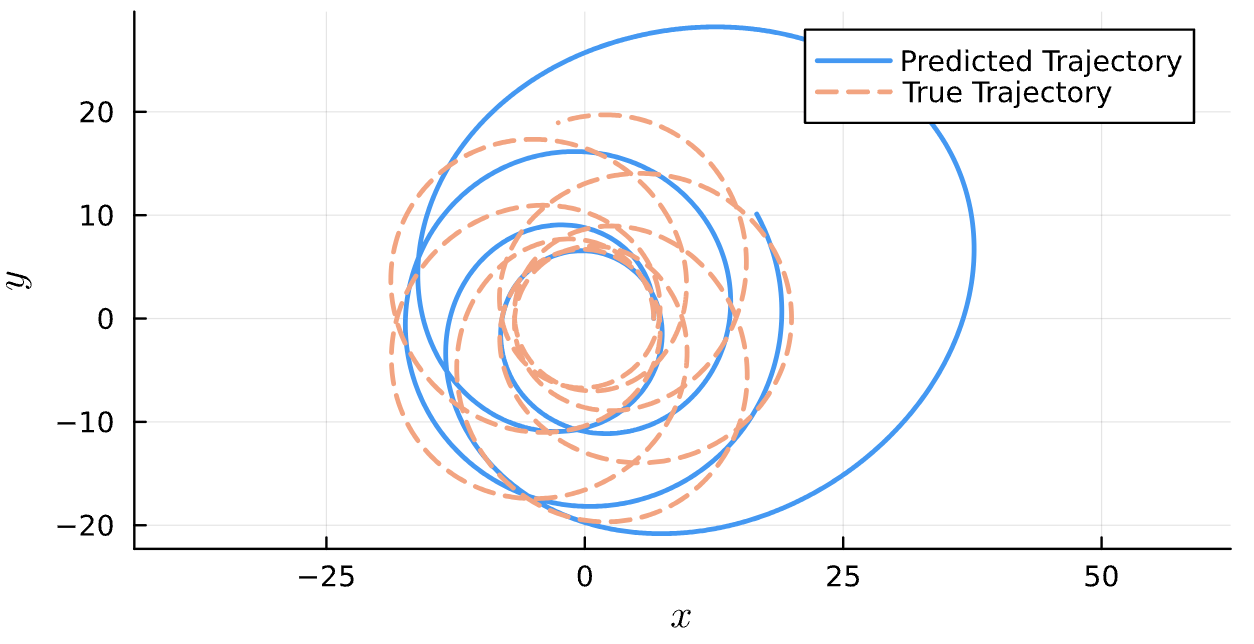
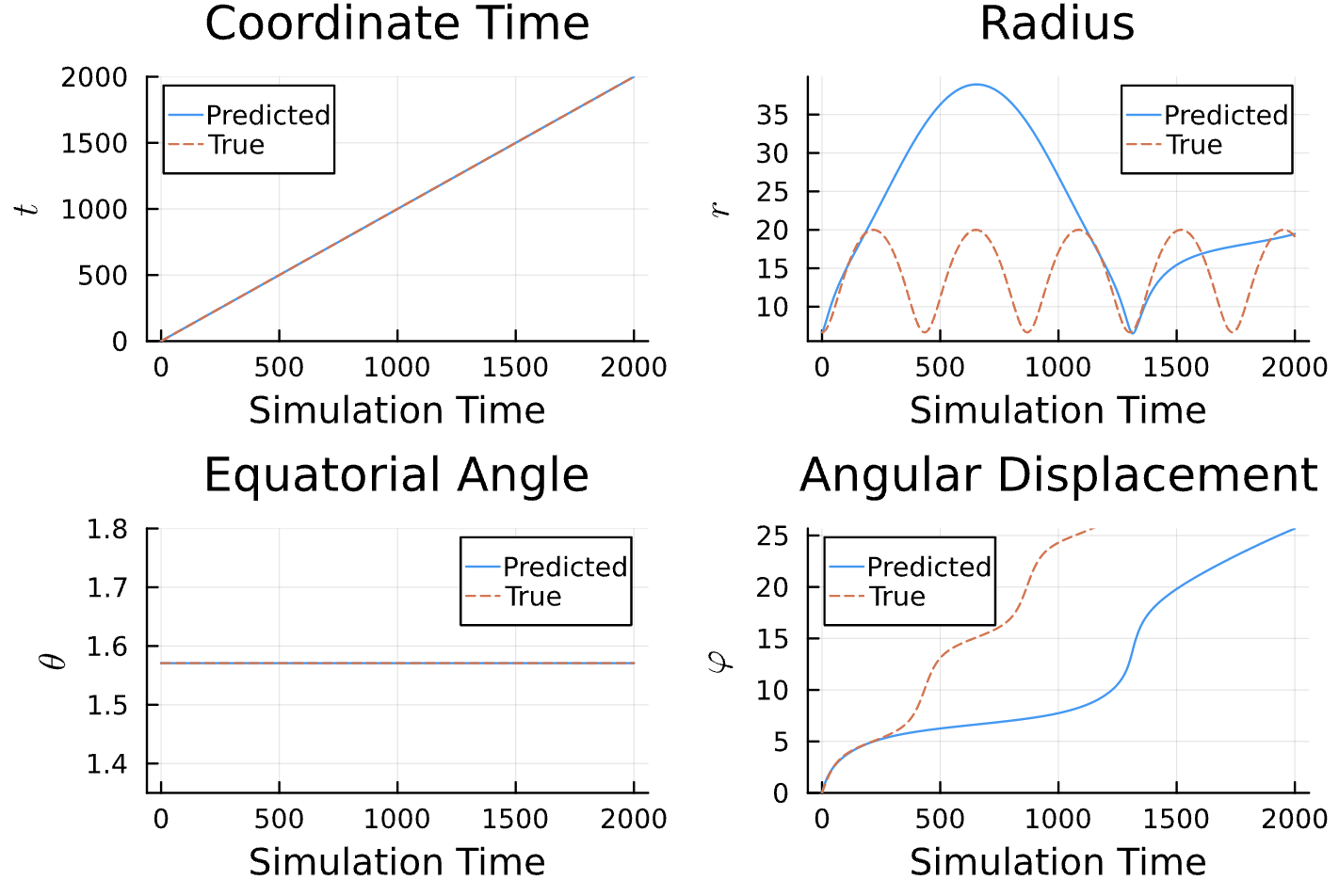
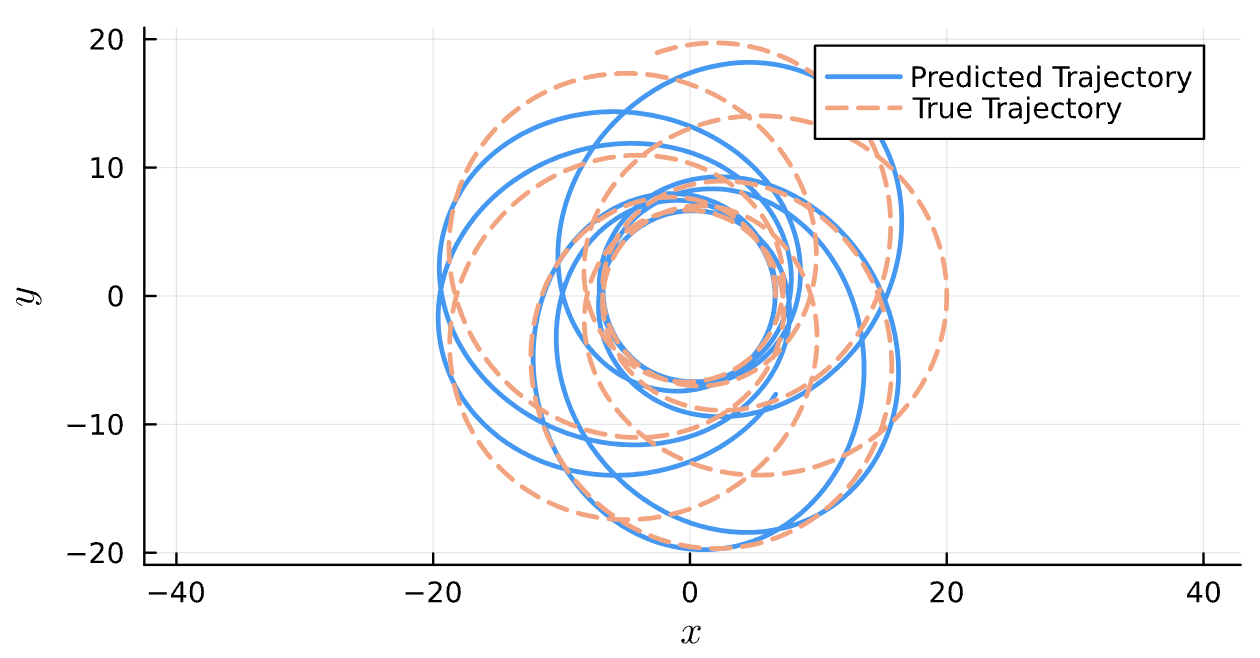
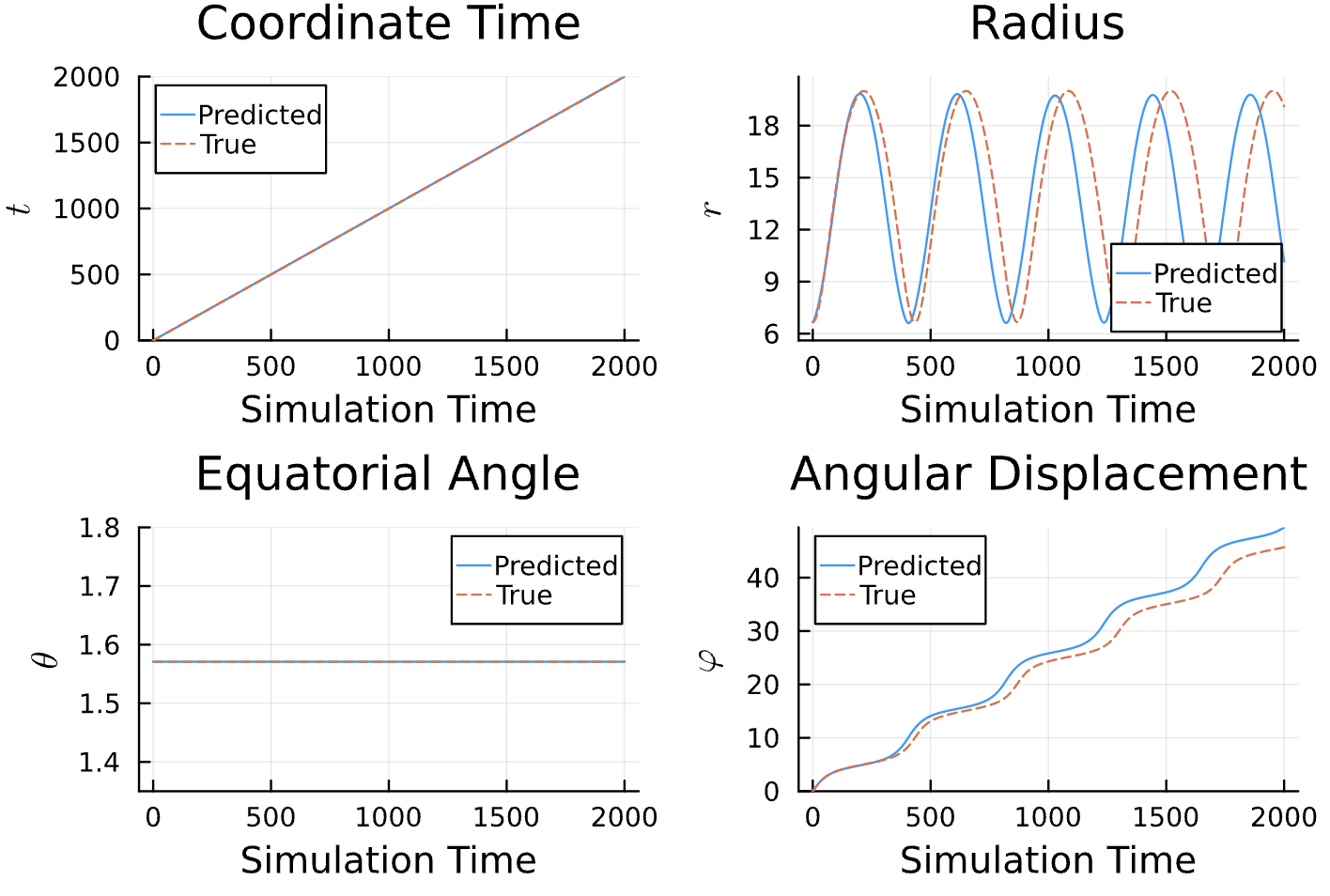
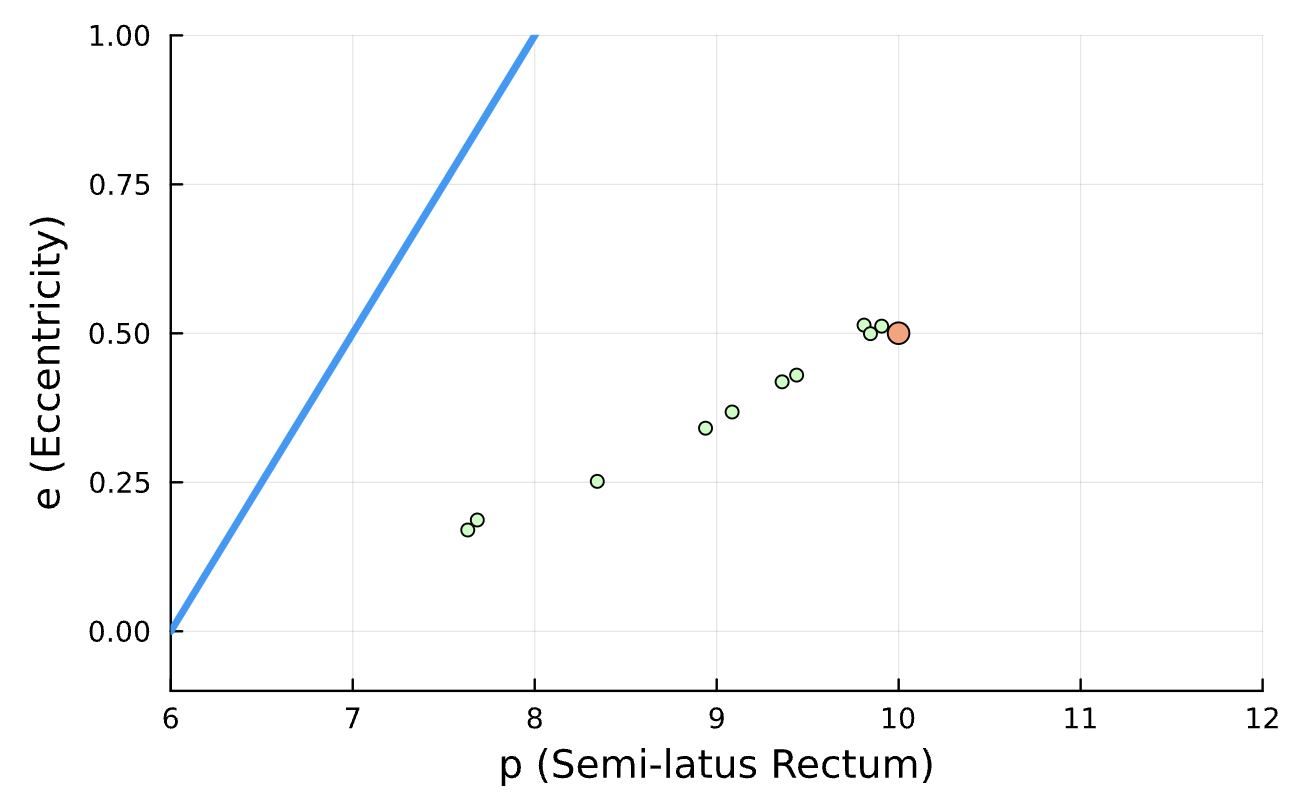
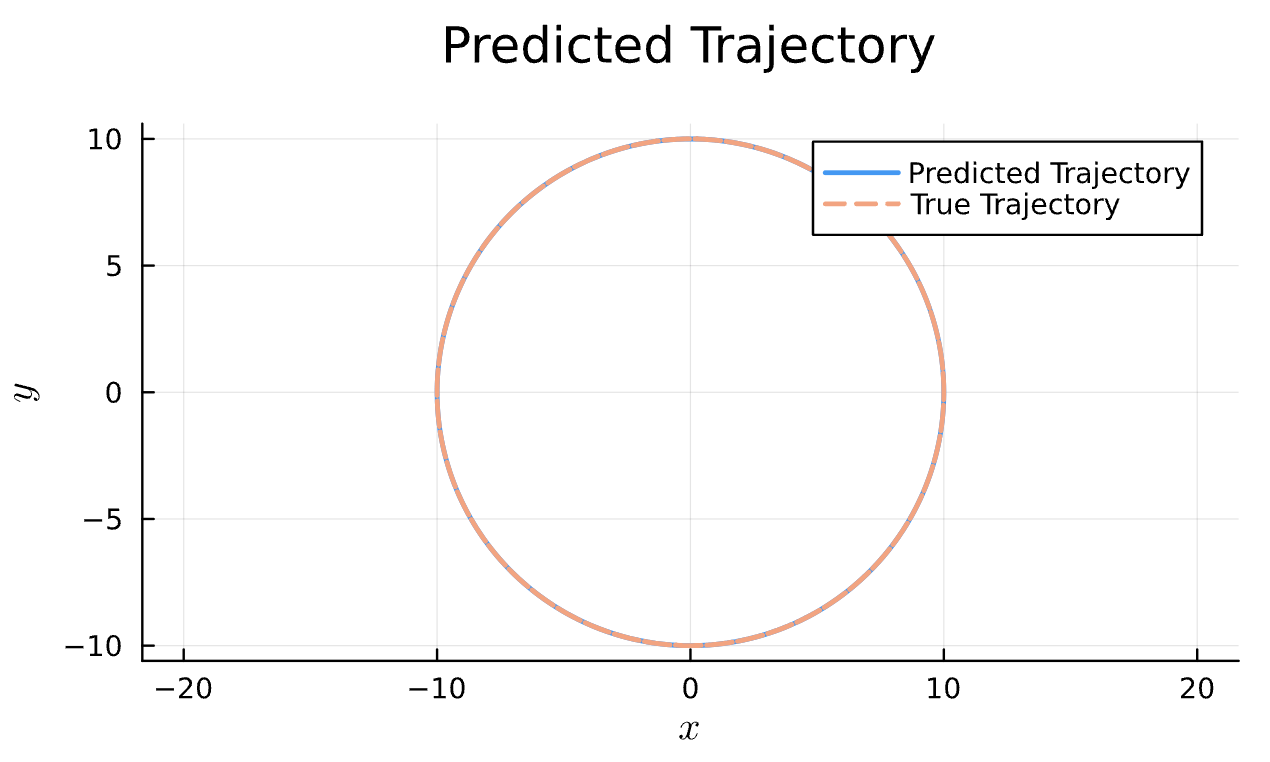
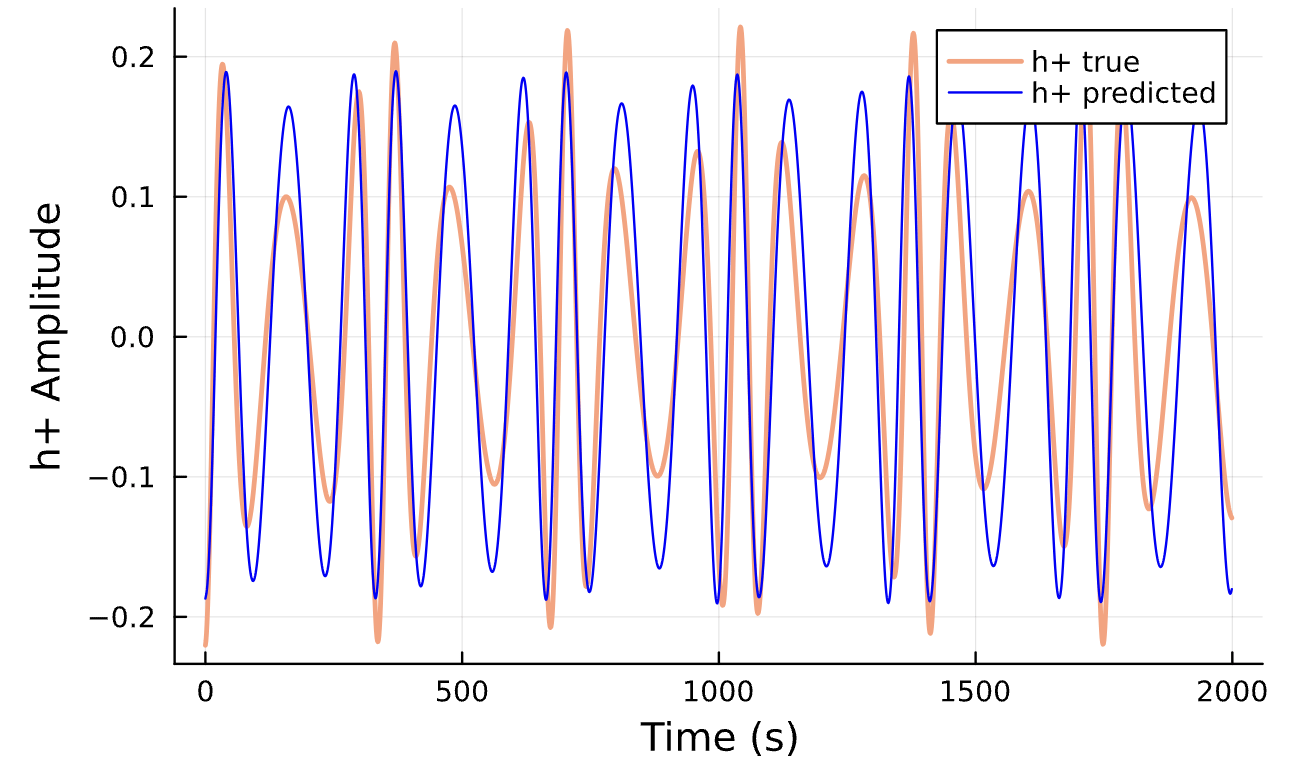
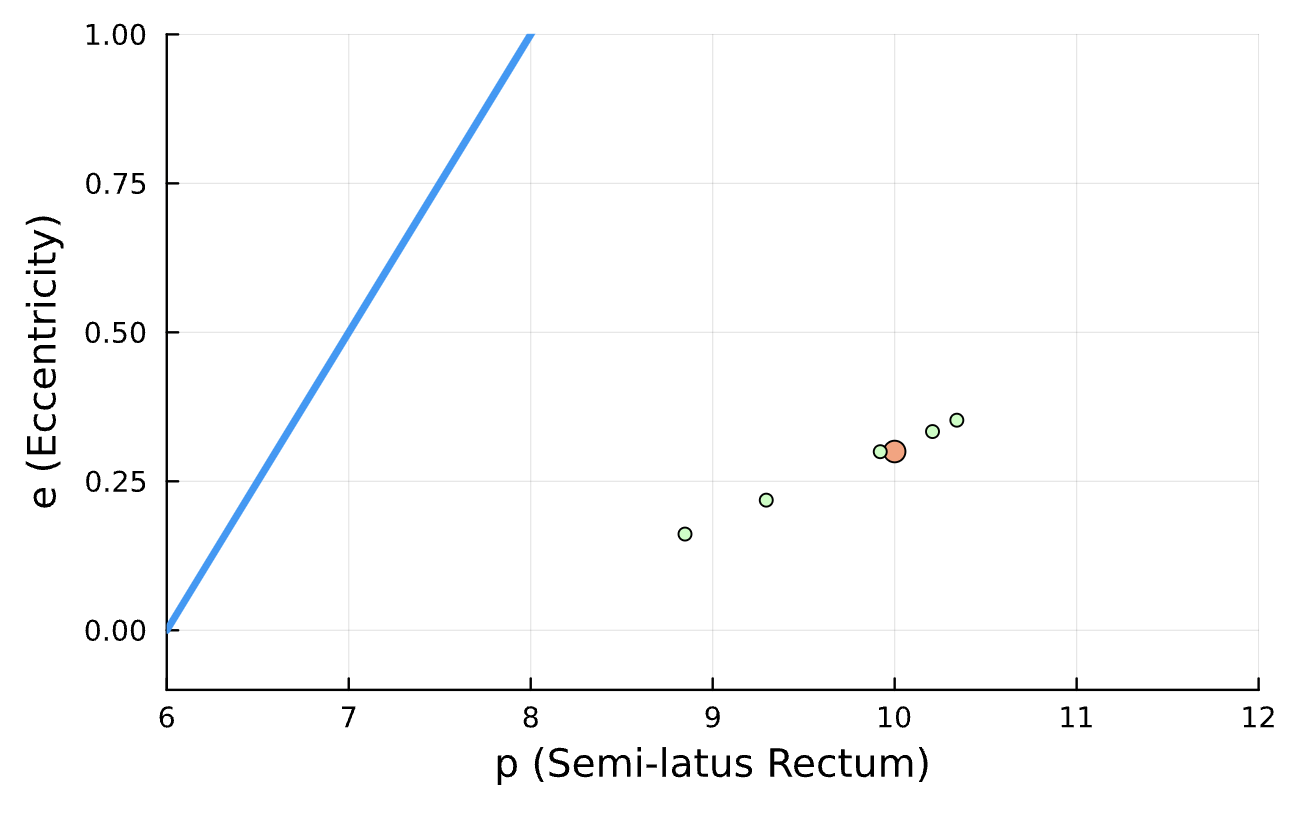
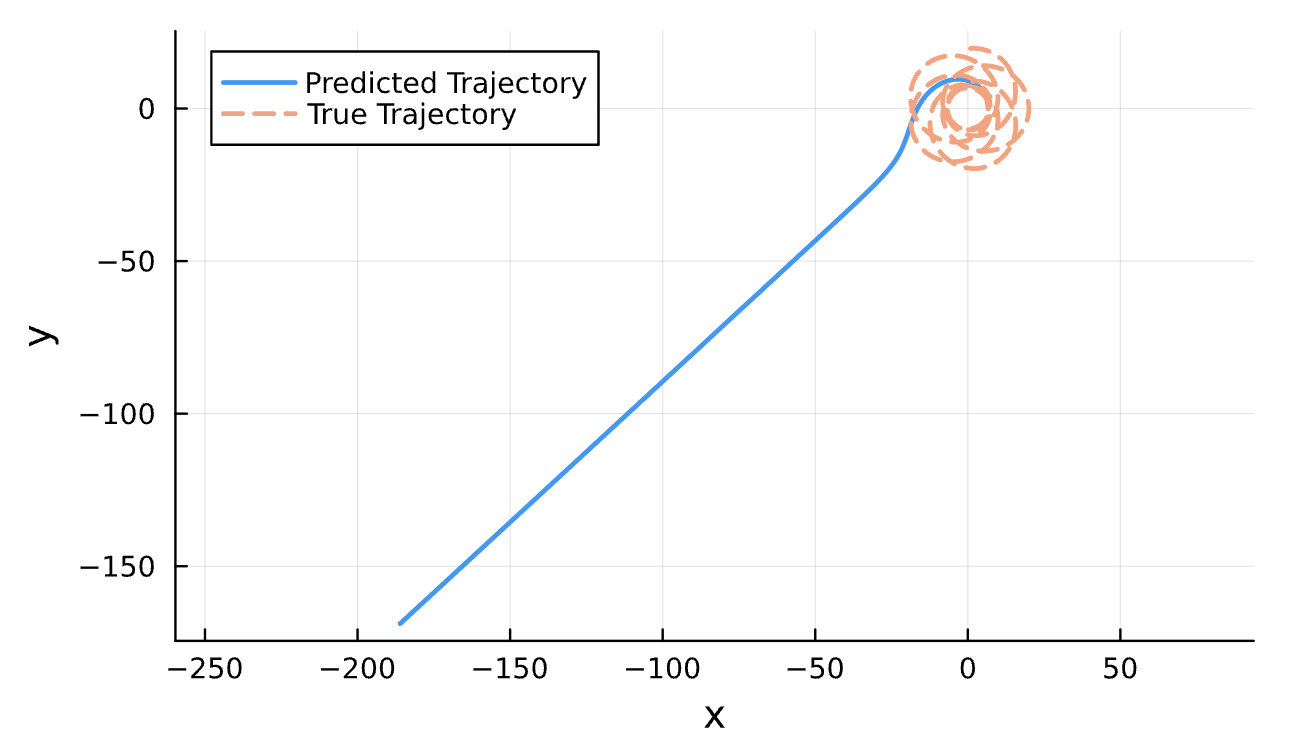
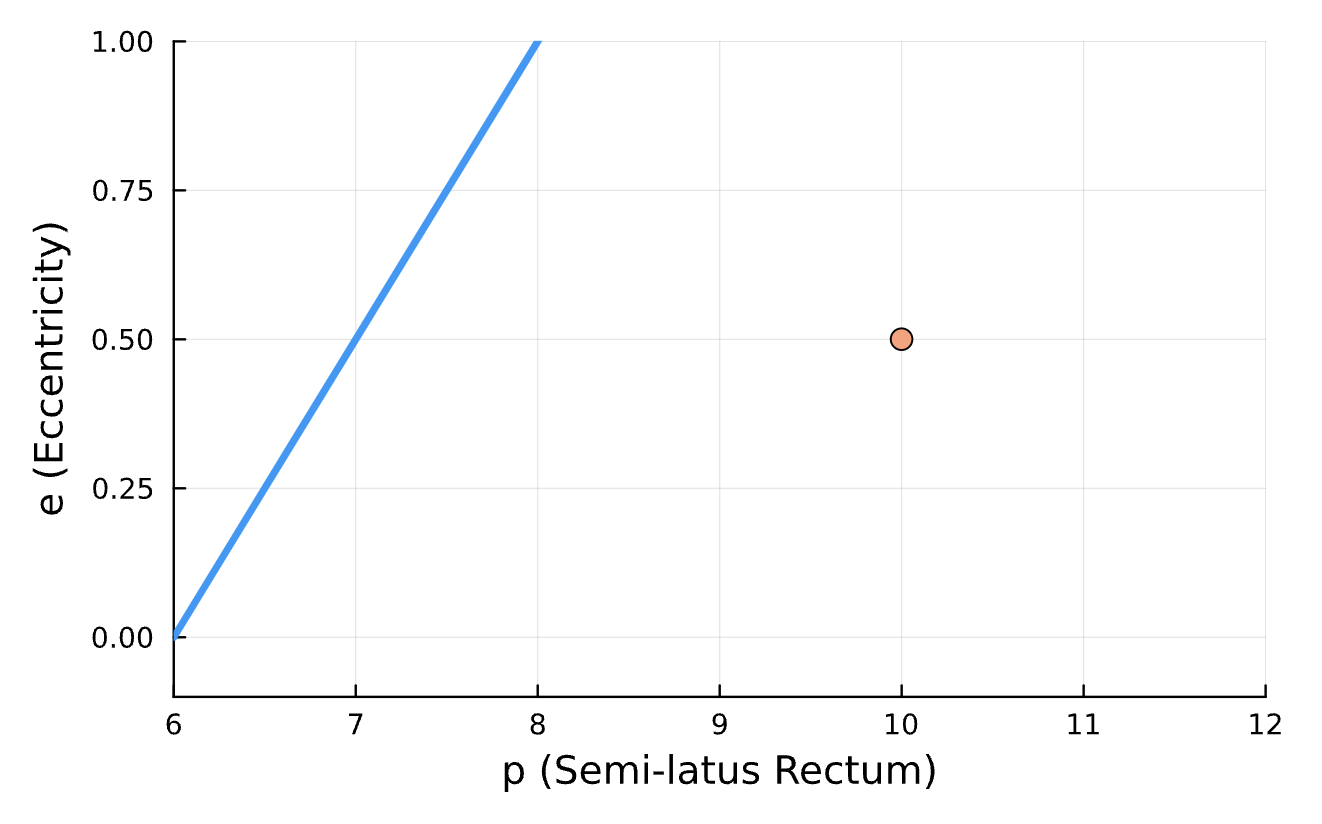
True (p = 100, e = 0.5); Guess (p = 100, e = 0.5)

Results




Learning Rate = 1e-2, Epochs = 5, # Iterations = 14, Training = 10% ~ 200/2000 time steps

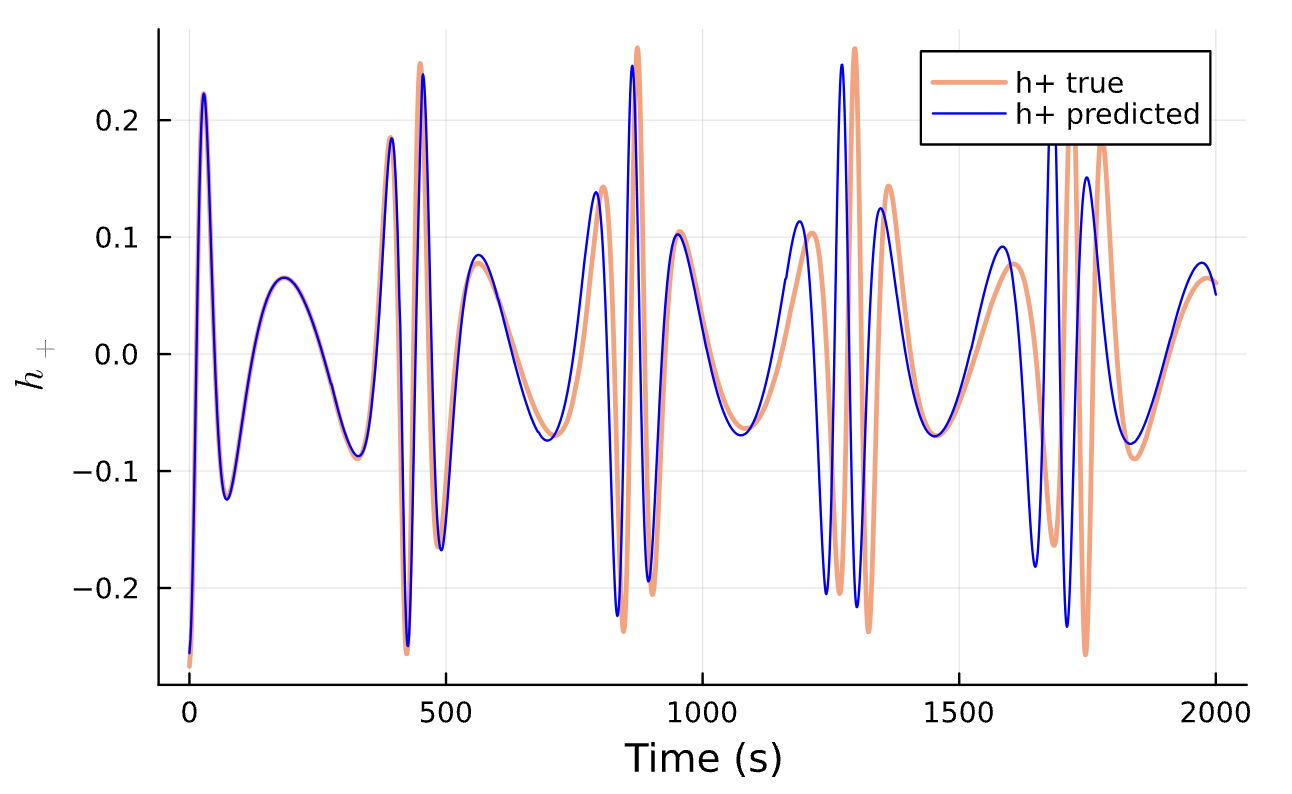
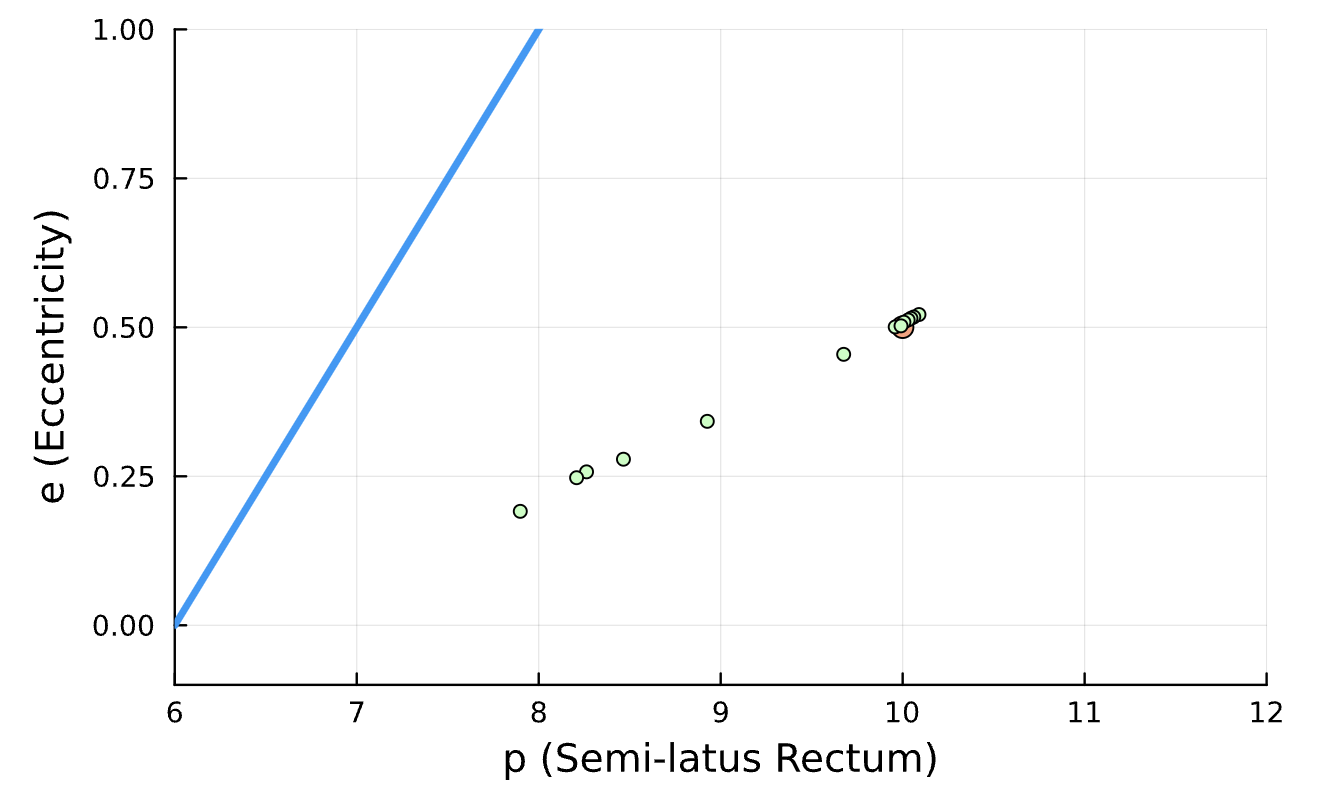
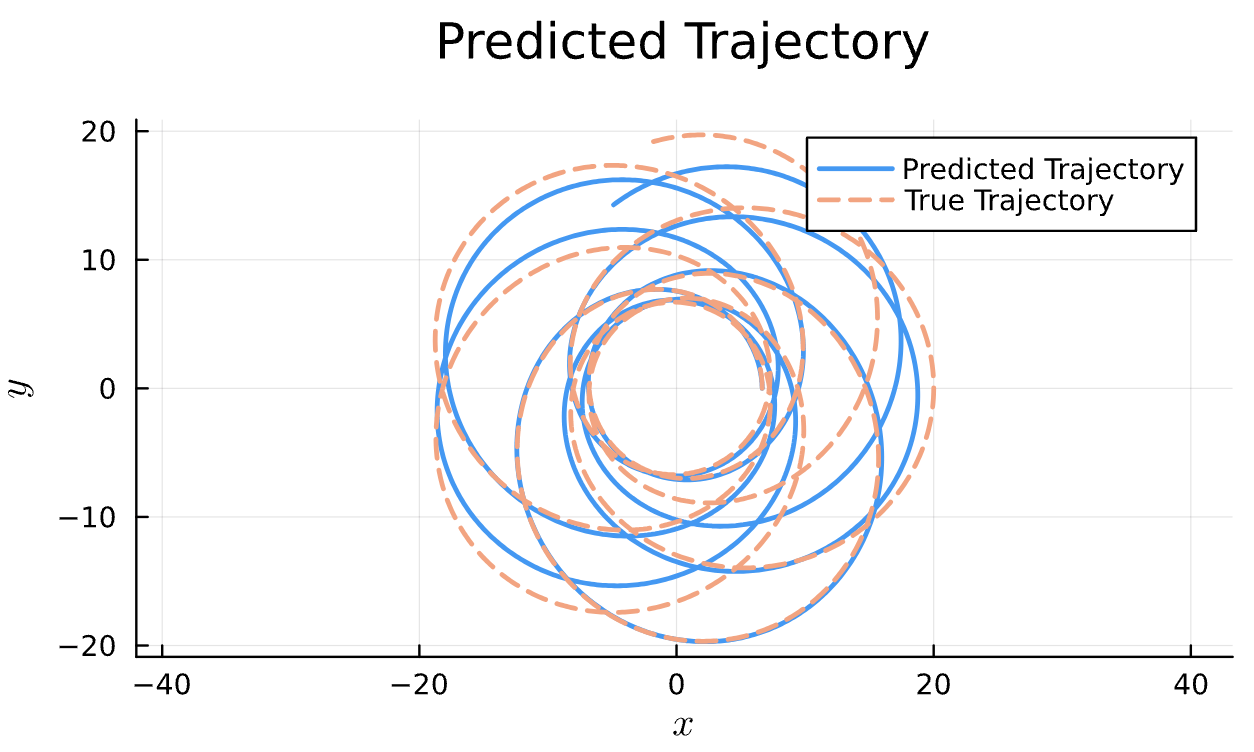
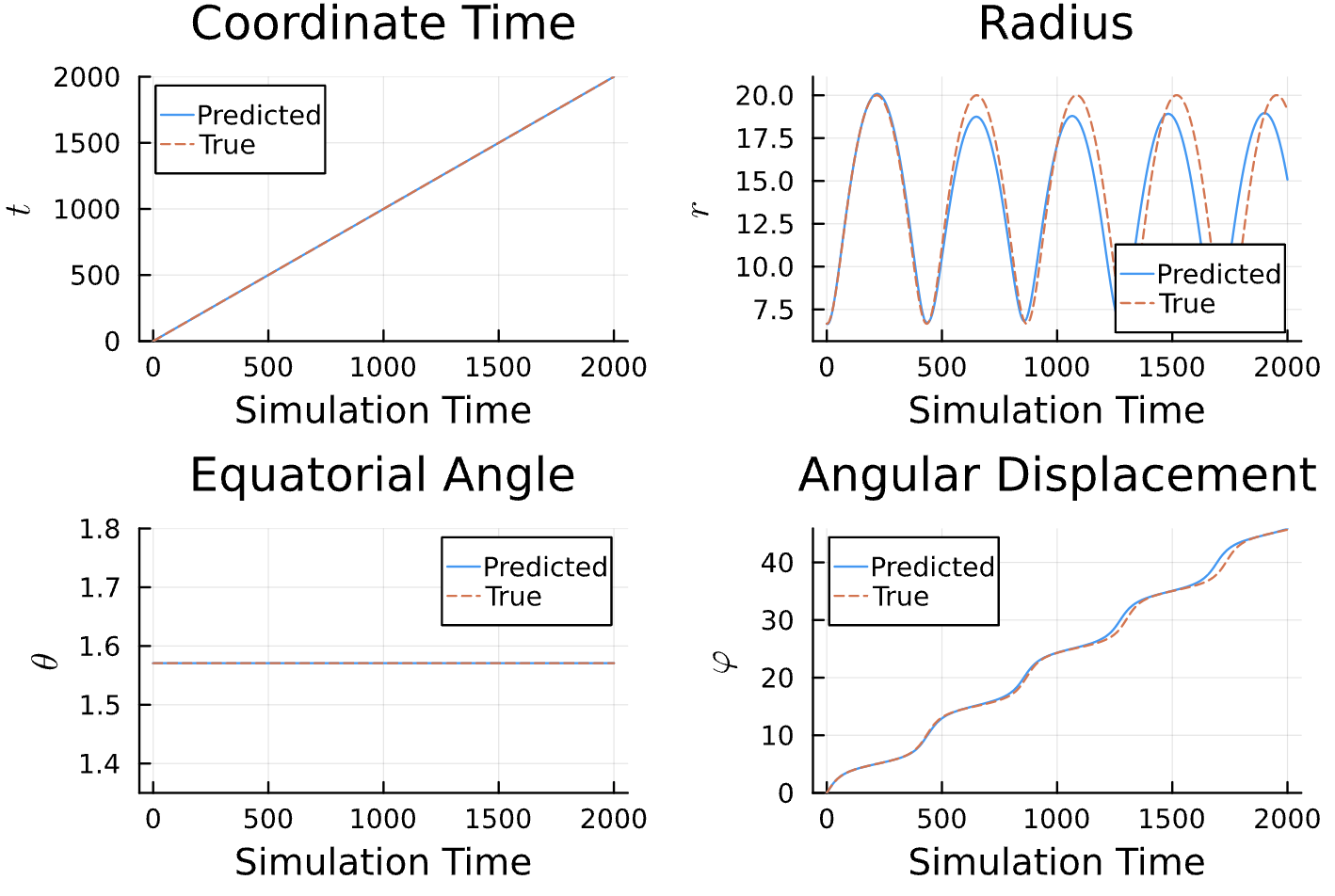
True (p = 100, e = 0.5); Guess (p = 100, e = 0.5)
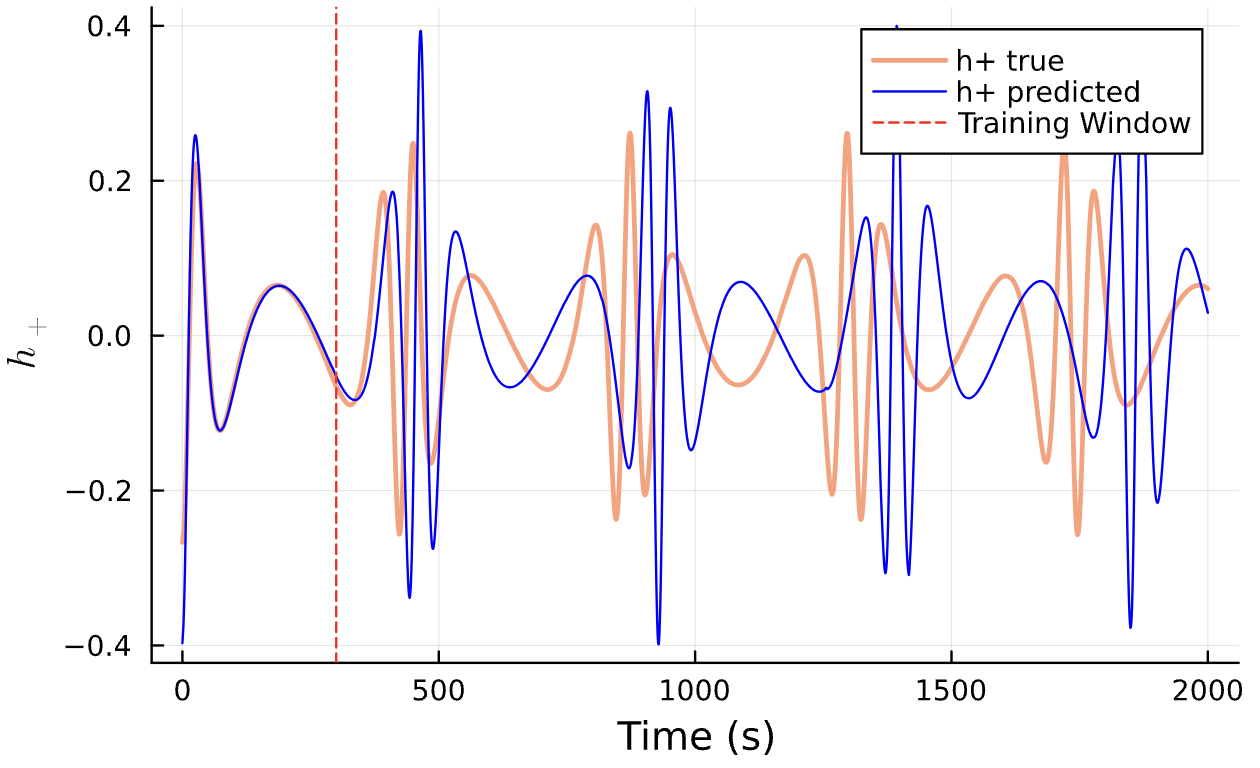
Training Window

Results




Learning Rate = 9e-3, Epochs = 6, # Iterations = 16, Training = 11% ~ 220/2000 time steps





True (p = 100, e = 0.5); Guess (p = 100, e = 0.5)
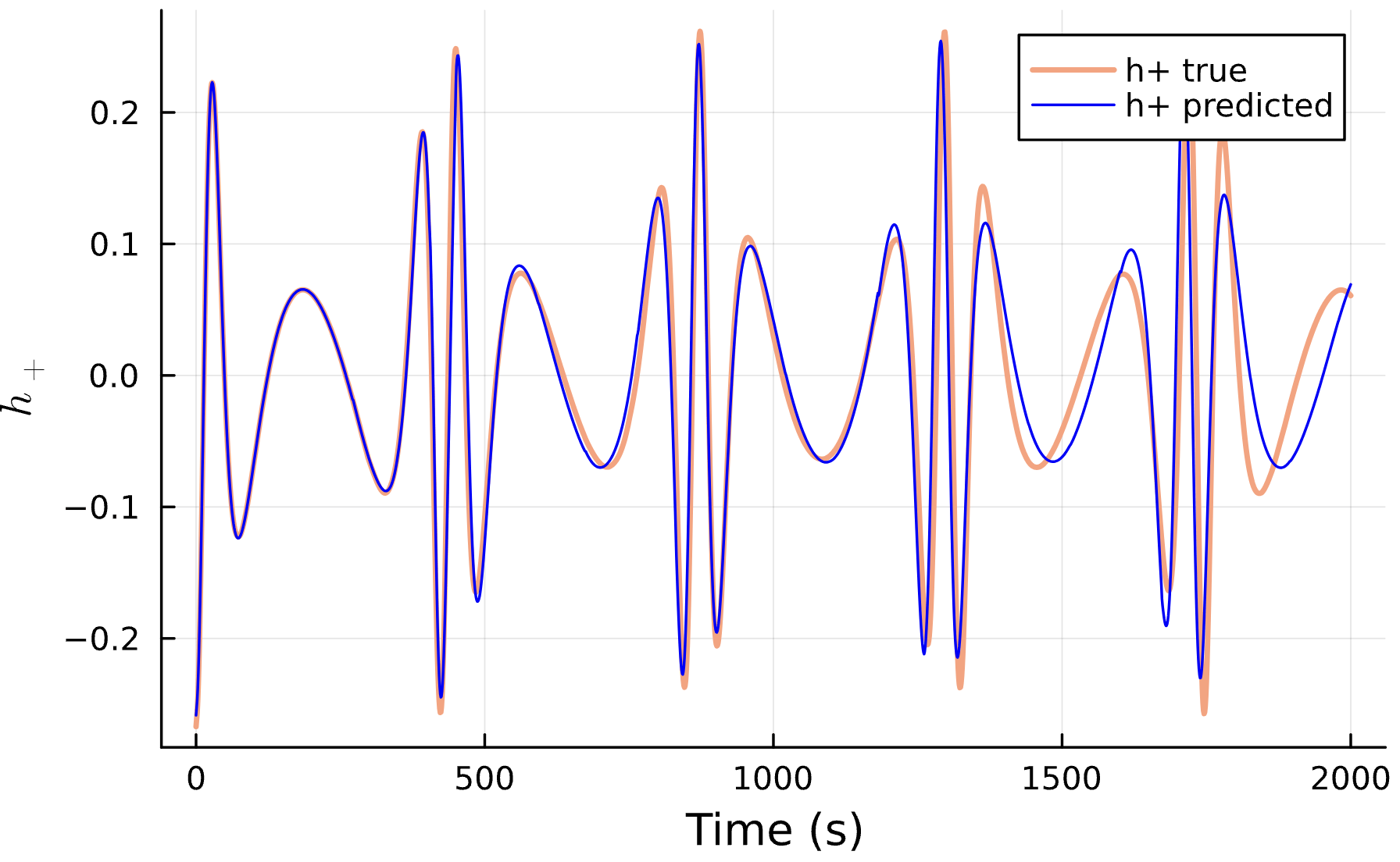
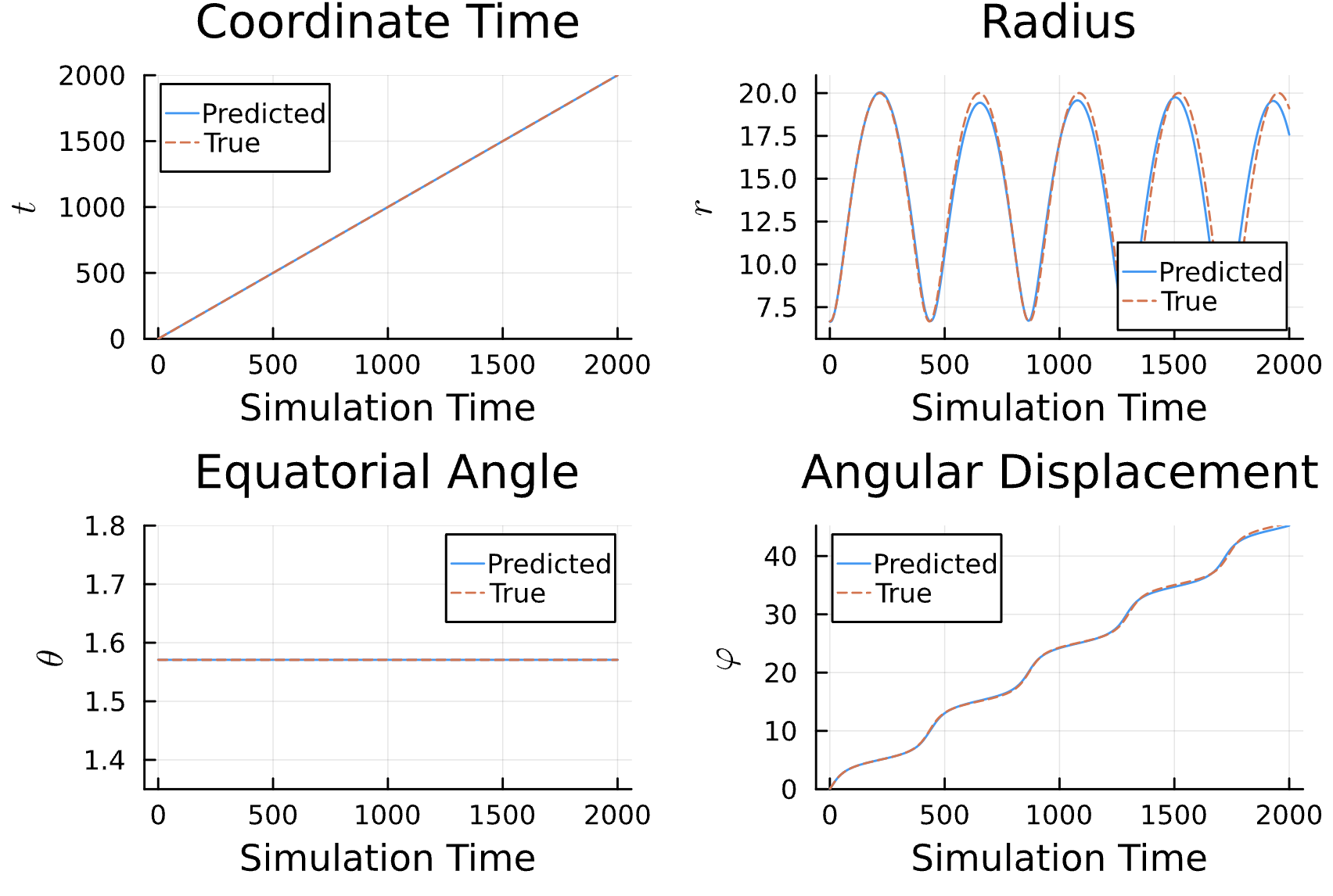
Training Window

Results
- Learning Rate = 1e-2
- Epochs = 5
- # Iterations = 14
- Training = 10% ~ 200/2000 secs

True (p = 100, e = 0.5); Guess (p = 100, e = 0.5)

- Learning Rate = 9e-3
- Epochs = 6
- # Iterations = 16
- Training = 11% ~ 220/2000 secs

Results
- Learning Rate = 1e-2
- Epochs = 5
- # Iterations = 14
- Training = 10% ~ 200/2000 secs

True (p = 100, e = 0.5); Guess (p = 100, e = 0.5)

- Learning Rate = 9e-3
- Epochs = 6
- # Iterations = 16
- Training = 11% ~ 220/2000 secs

Results*
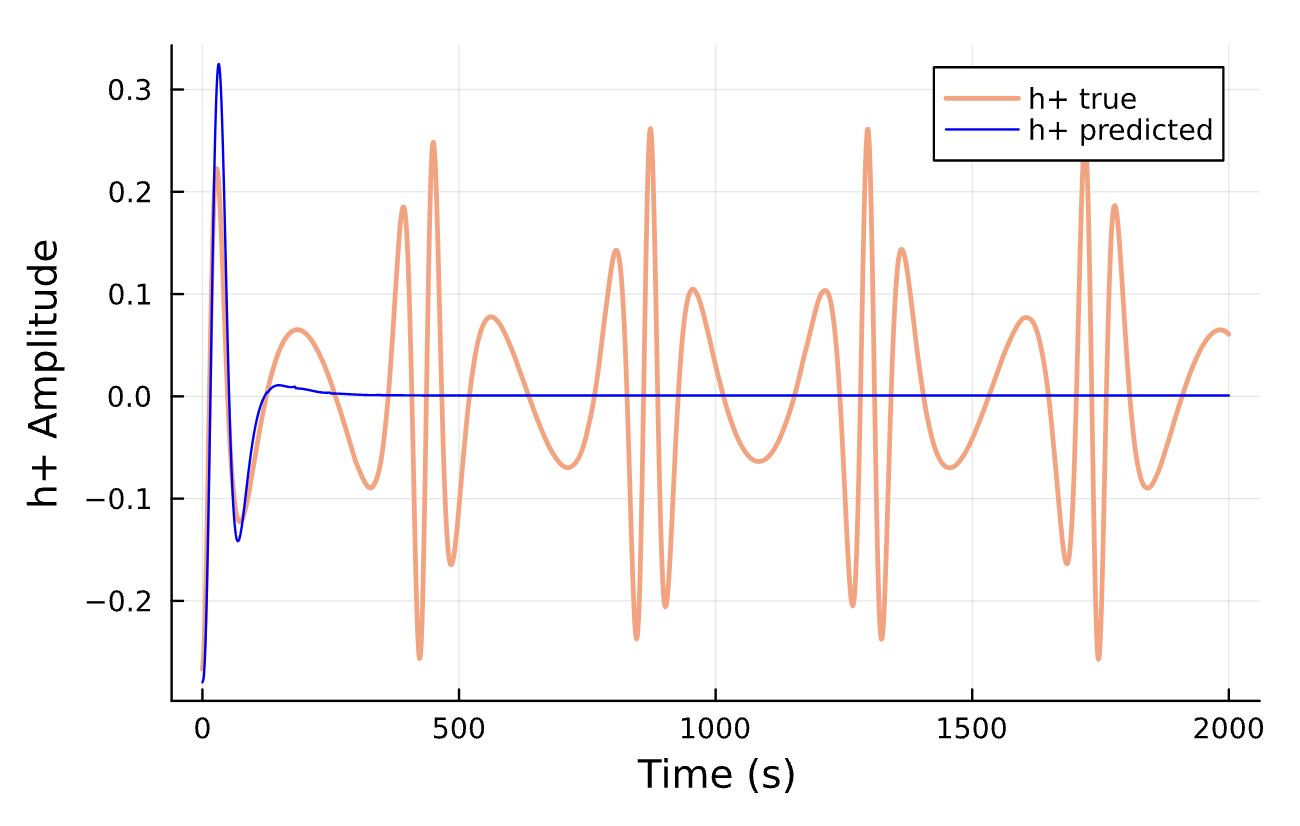
Learning Rate = 1e-2, Epochs = 5, # Iterations = 5, Training = 5% ~ 100/2000 time steps
True (p = 100, e = 0.5); Guess (p = 100, e = 0.5) *Neural Network is fully handicapped
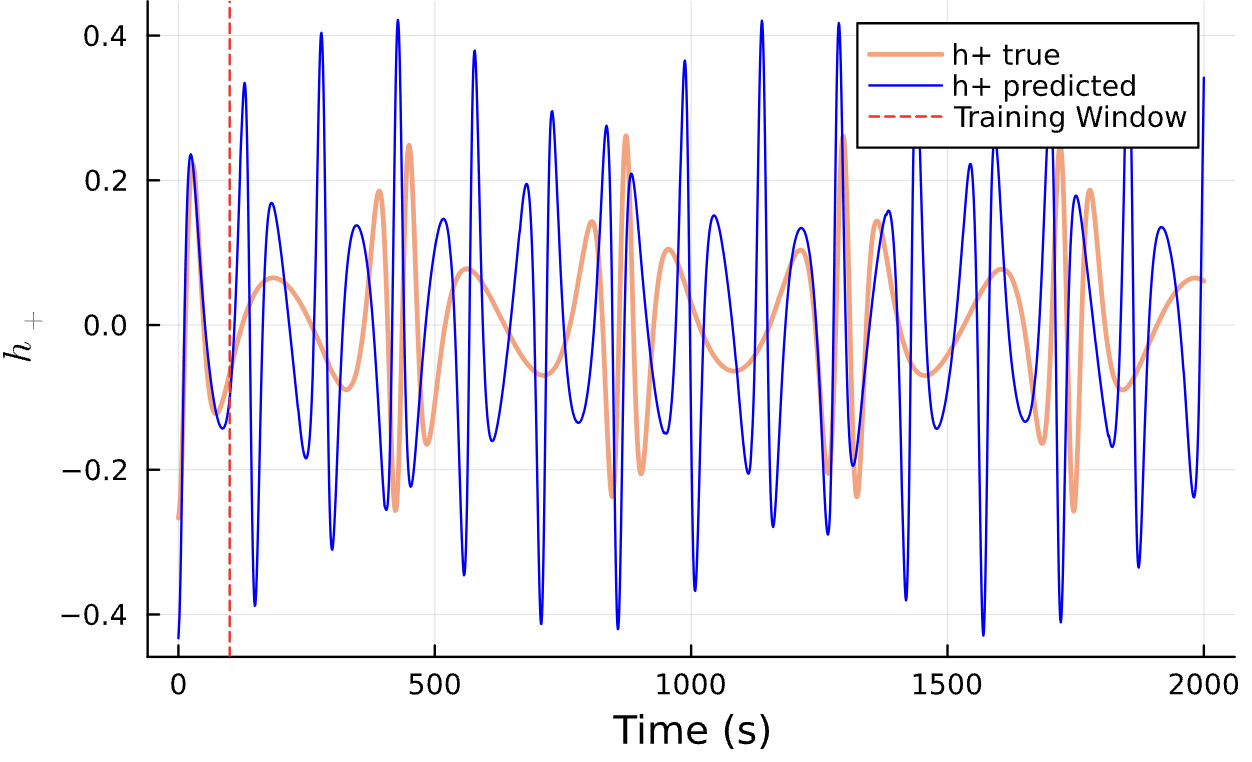

Results*
Learning Rate = 9e-3, Epochs = 7, # Iterations = 16, Training = 11% ~ 220/2000 time steps
True (p = 100, e = 0.5); Guess (p = 100, e = 0.5) *Neural Network is fully handicapped
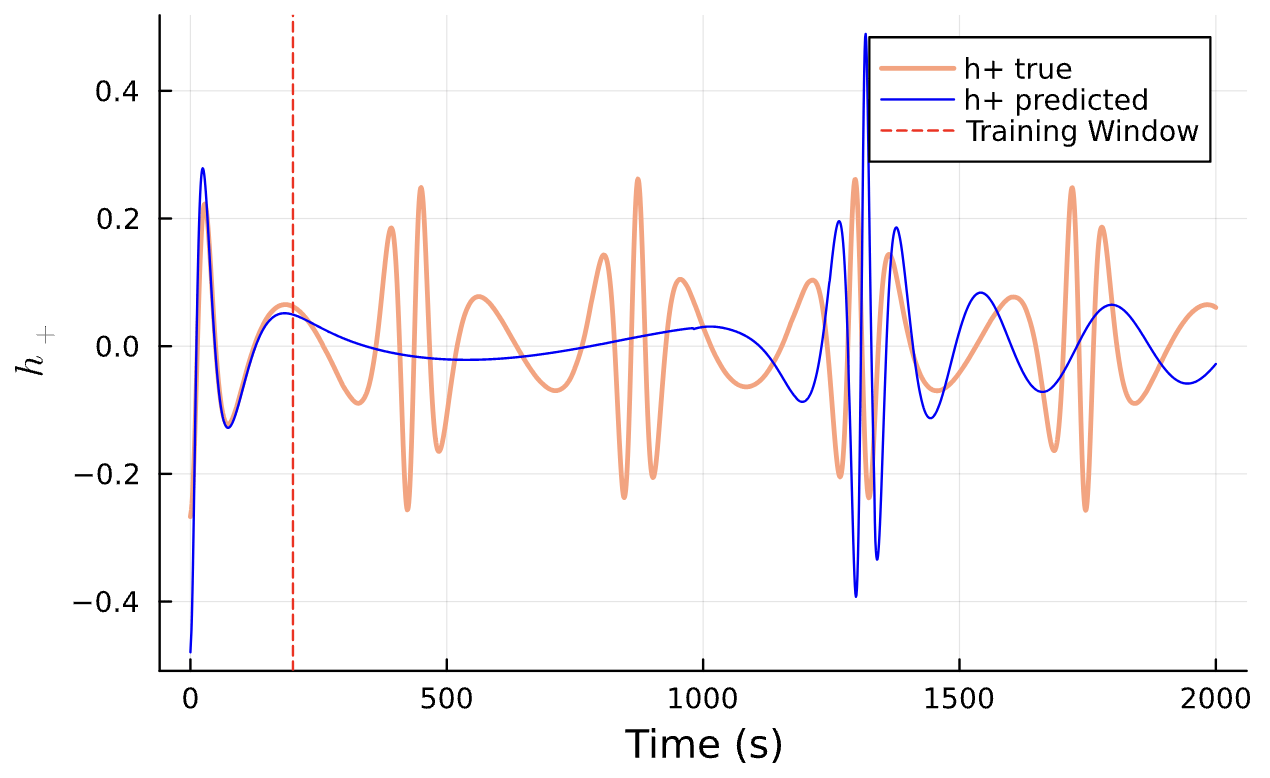
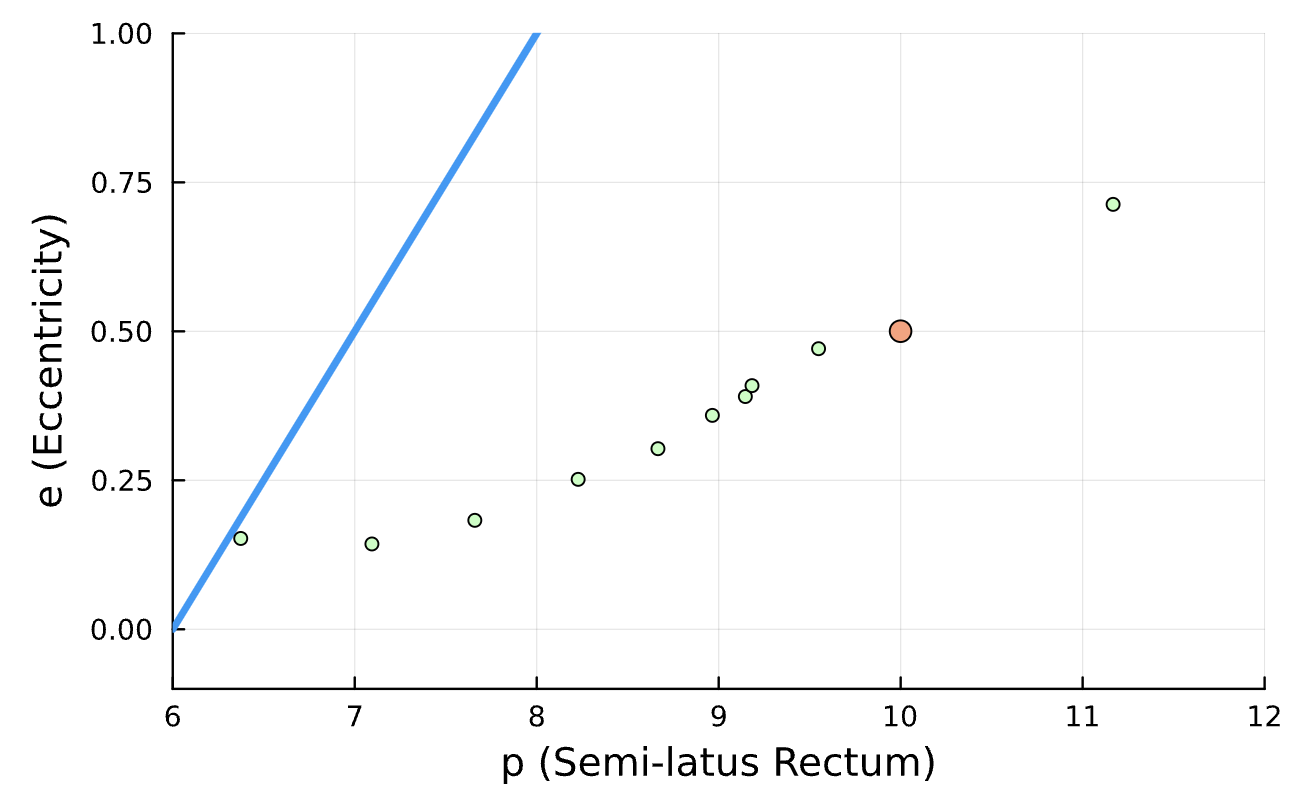

Results*
Learning Rate = 9e-3, Epochs = 7, # Iterations = 16, Training = 11% ~ 220/2000 time steps
True (p = 100, e = 0.5); Guess (p = 100, e = 0.5) *Neural Network is fully handicapped

Results*
Learning Rate = 9e-3, Epochs = 5, # Iterations = 10, Training = 15% ~ 300/2000 time steps
True (p = 100, e = 0.5); Guess (p = 100, e = 0.5) *Neural Network is fully handicapped

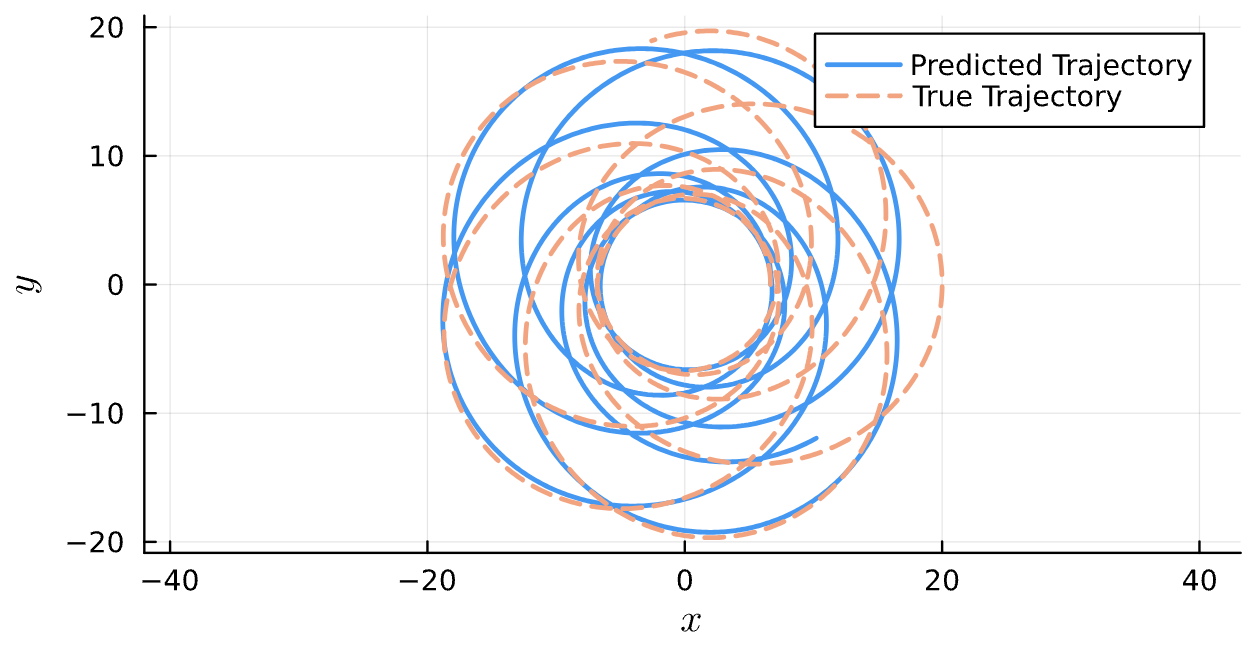
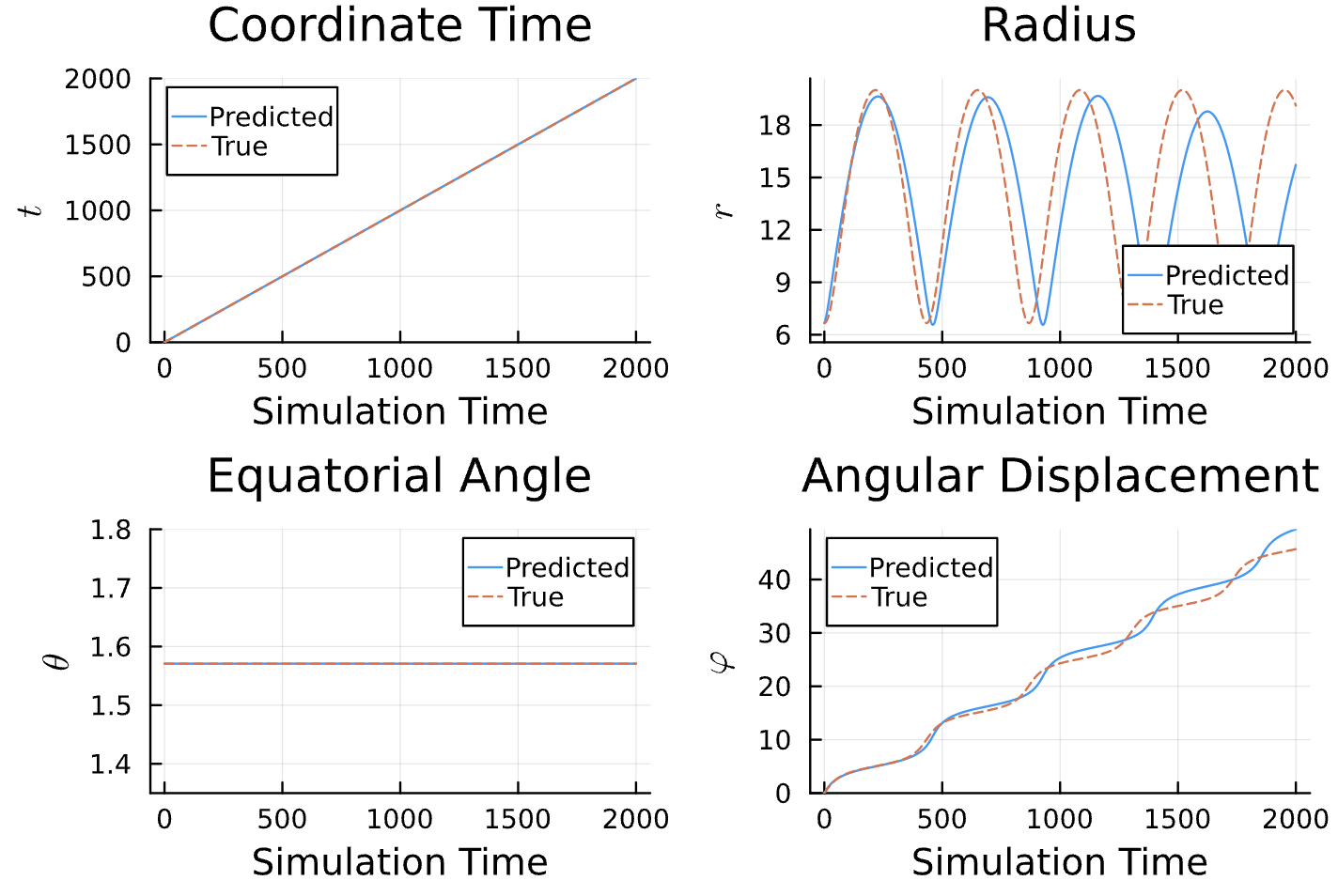

Results*
Learning Rate = 9e-3, Epochs = 5, # Iterations = 12, Training = 16% ~ 320/2000 time steps
True (p = 100, e = 0.5); Guess (p = 100, e = 0.5) *Neural Network is fully handicapped


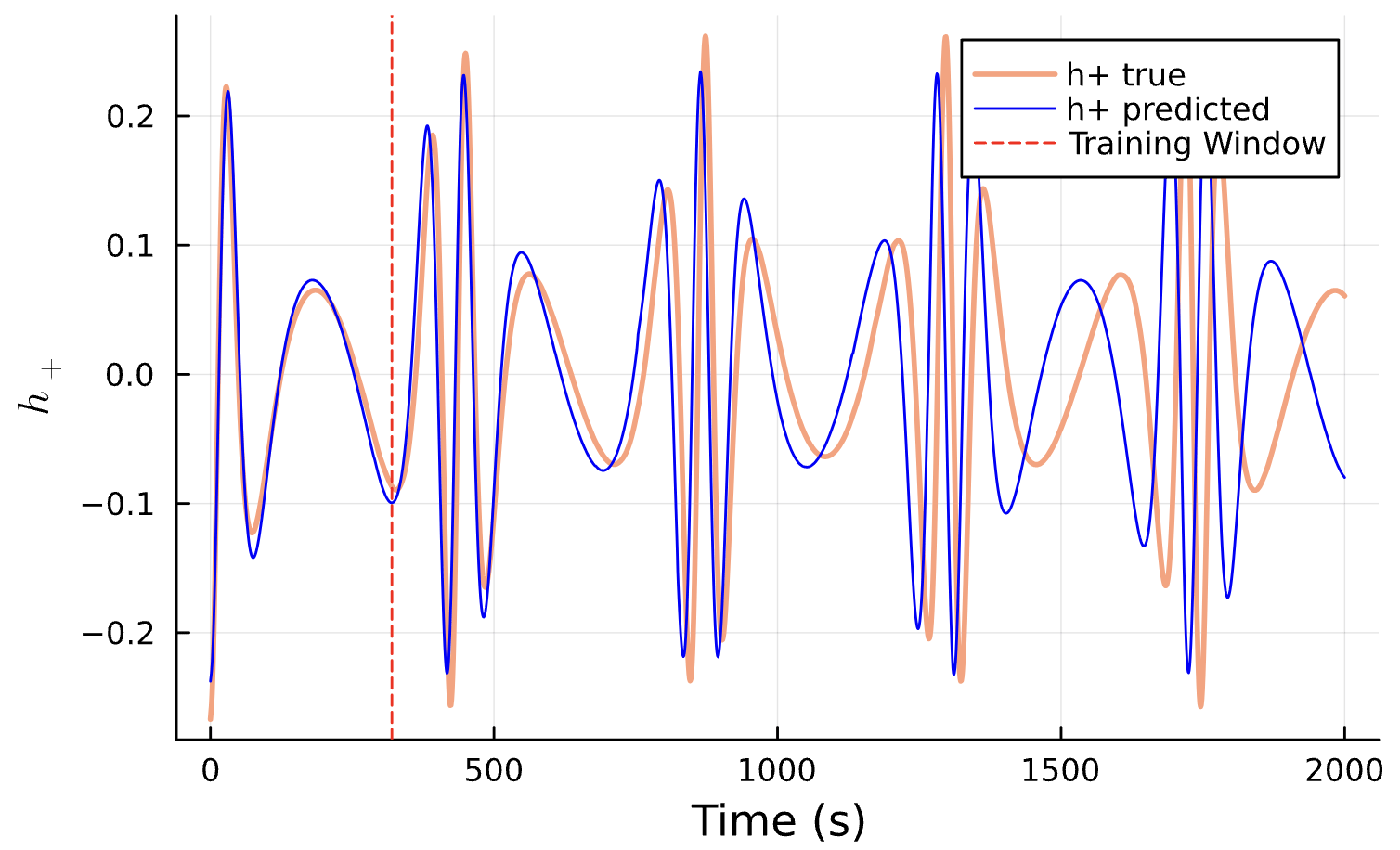
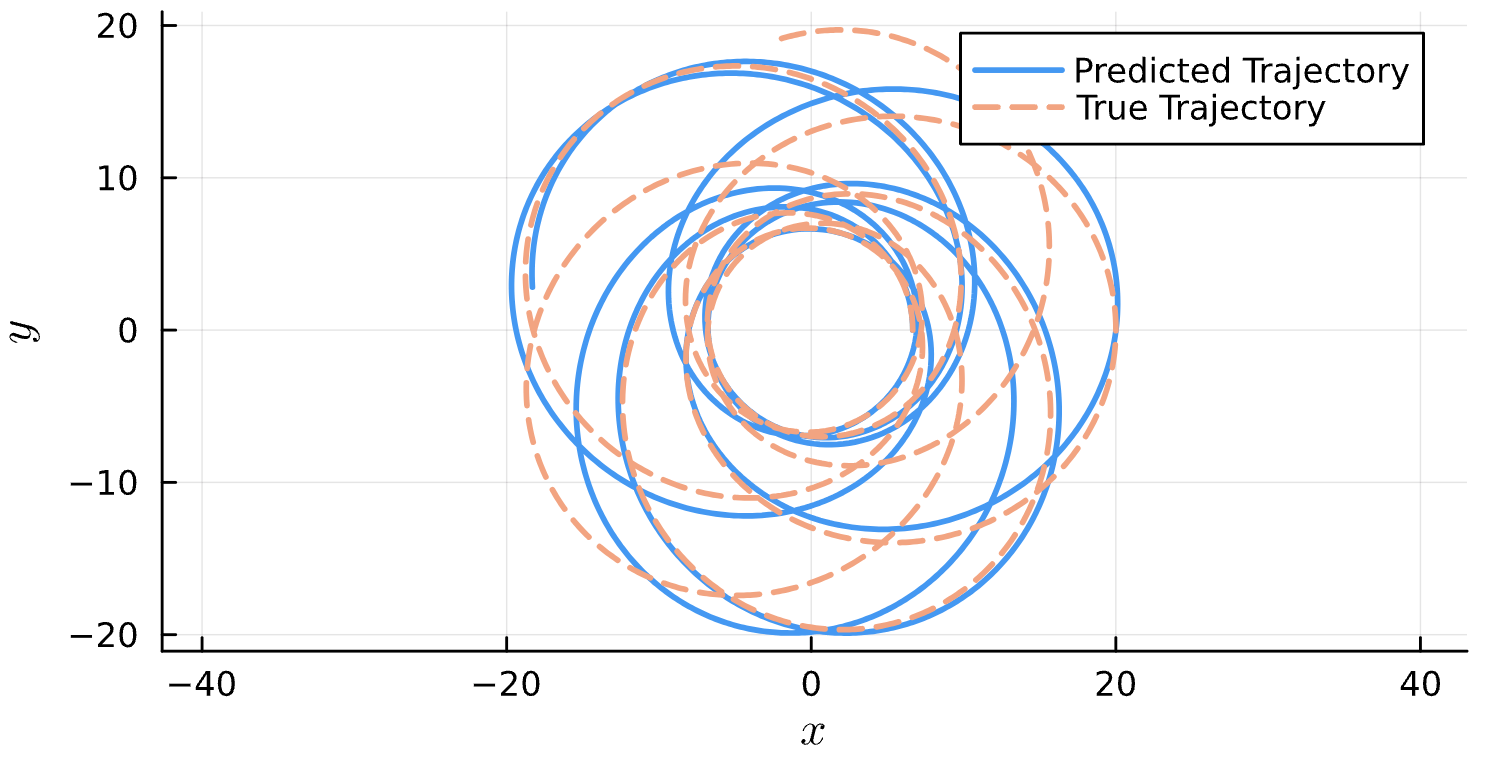
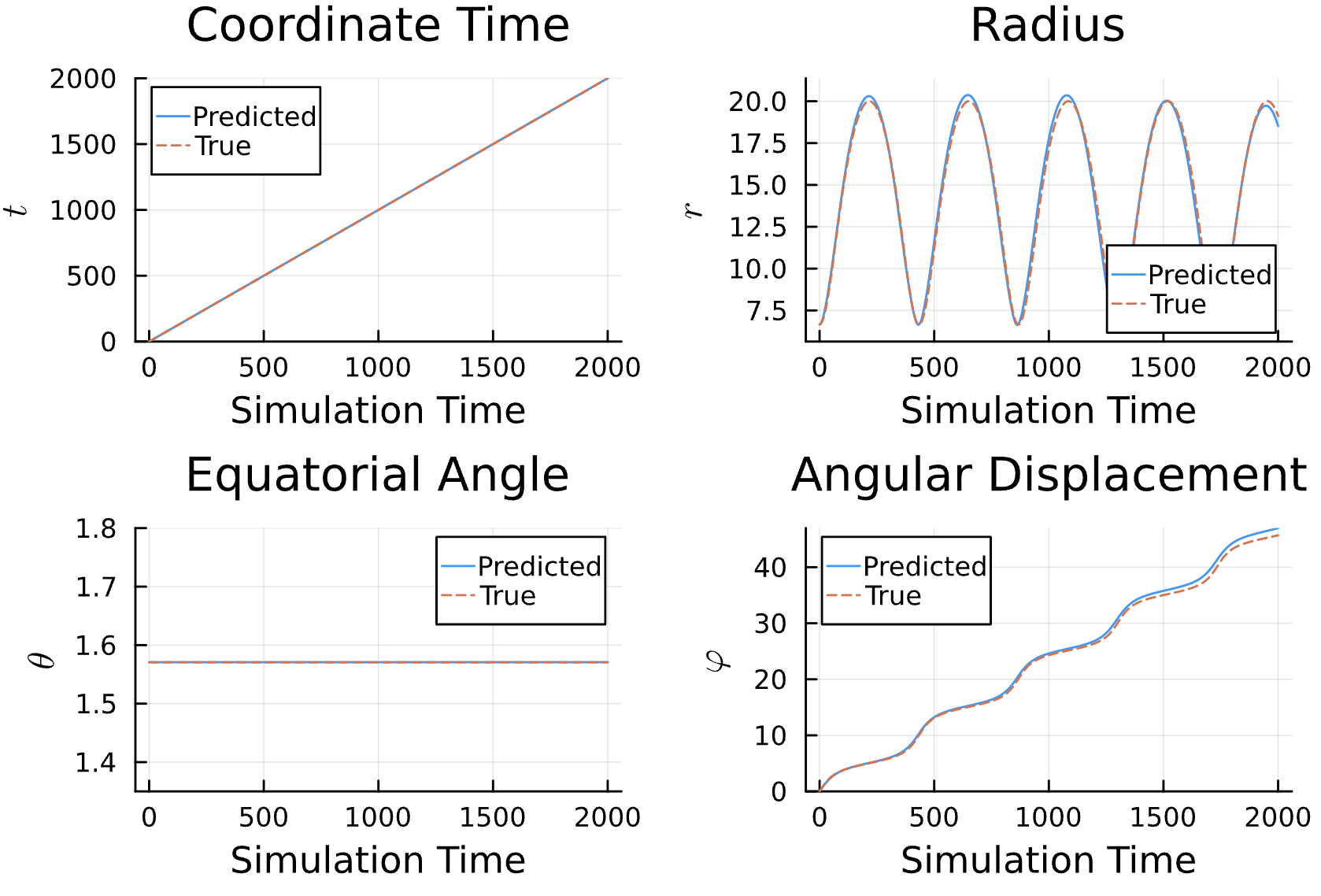

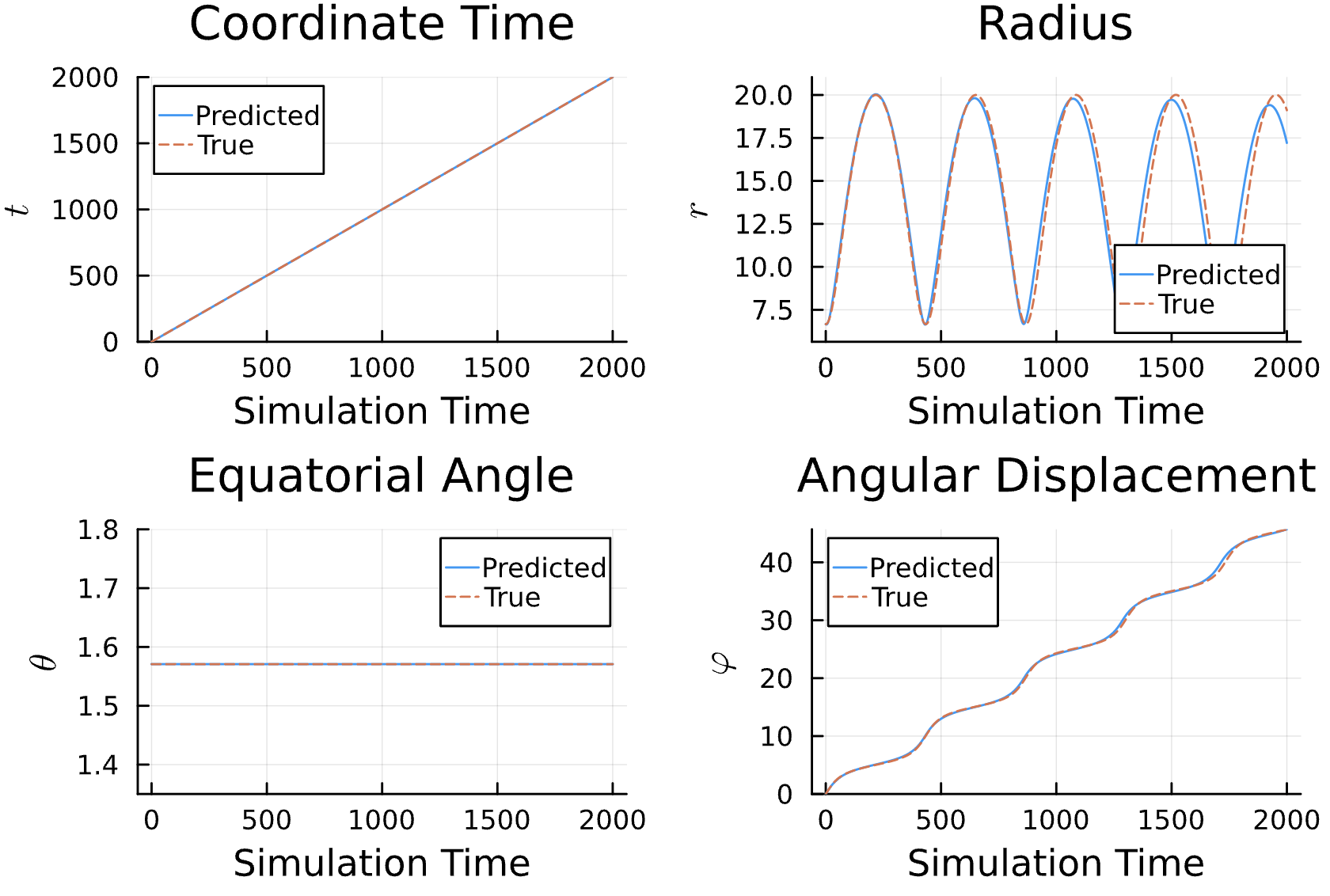
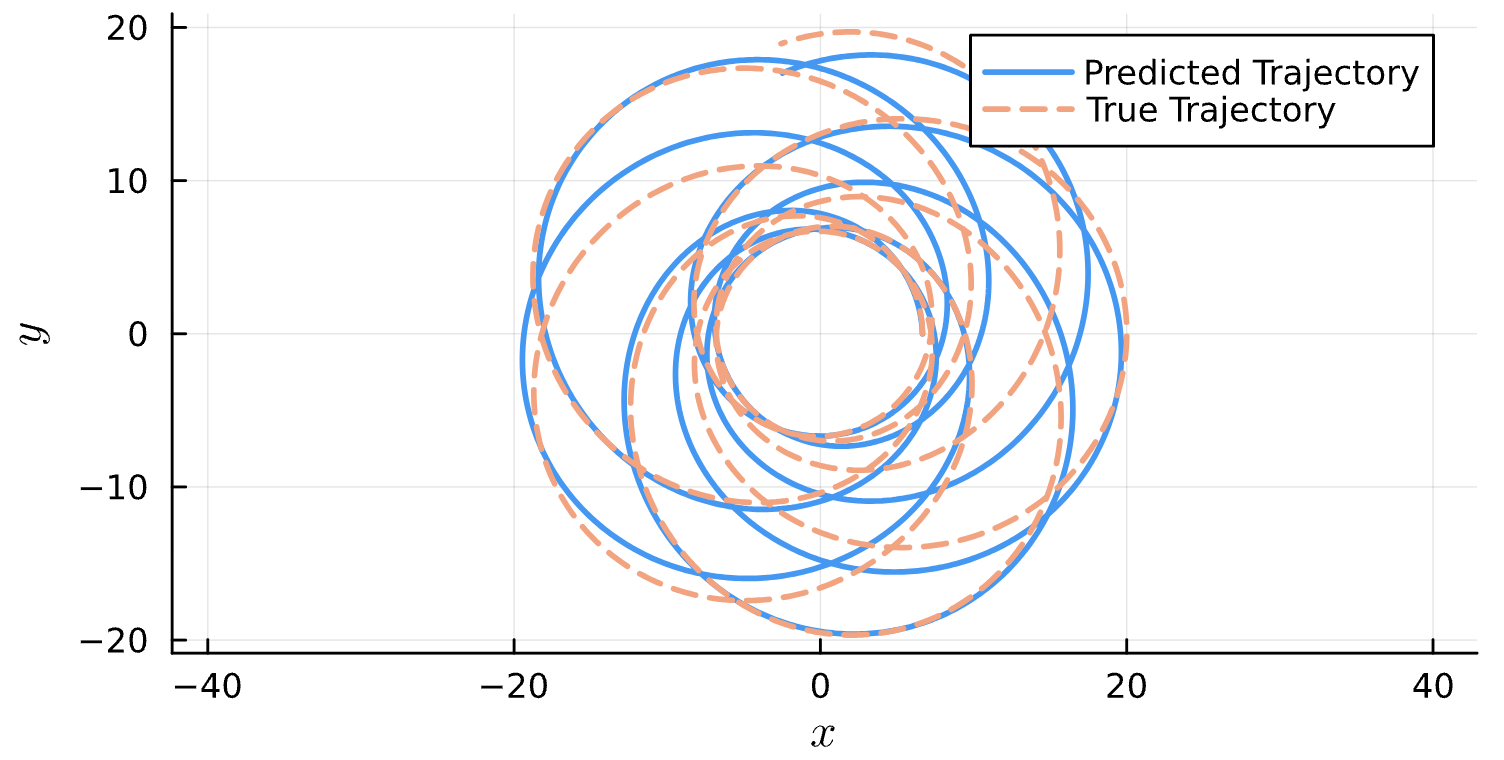
Results*
Learning Rate = 9e-3, Epochs = 6, # Iterations = 12, Training = 16% ~ 320/2000 time steps
True (p = 100, e = 0.5); Guess (p = 100, e = 0.5) *Neural Network is fully handicapped
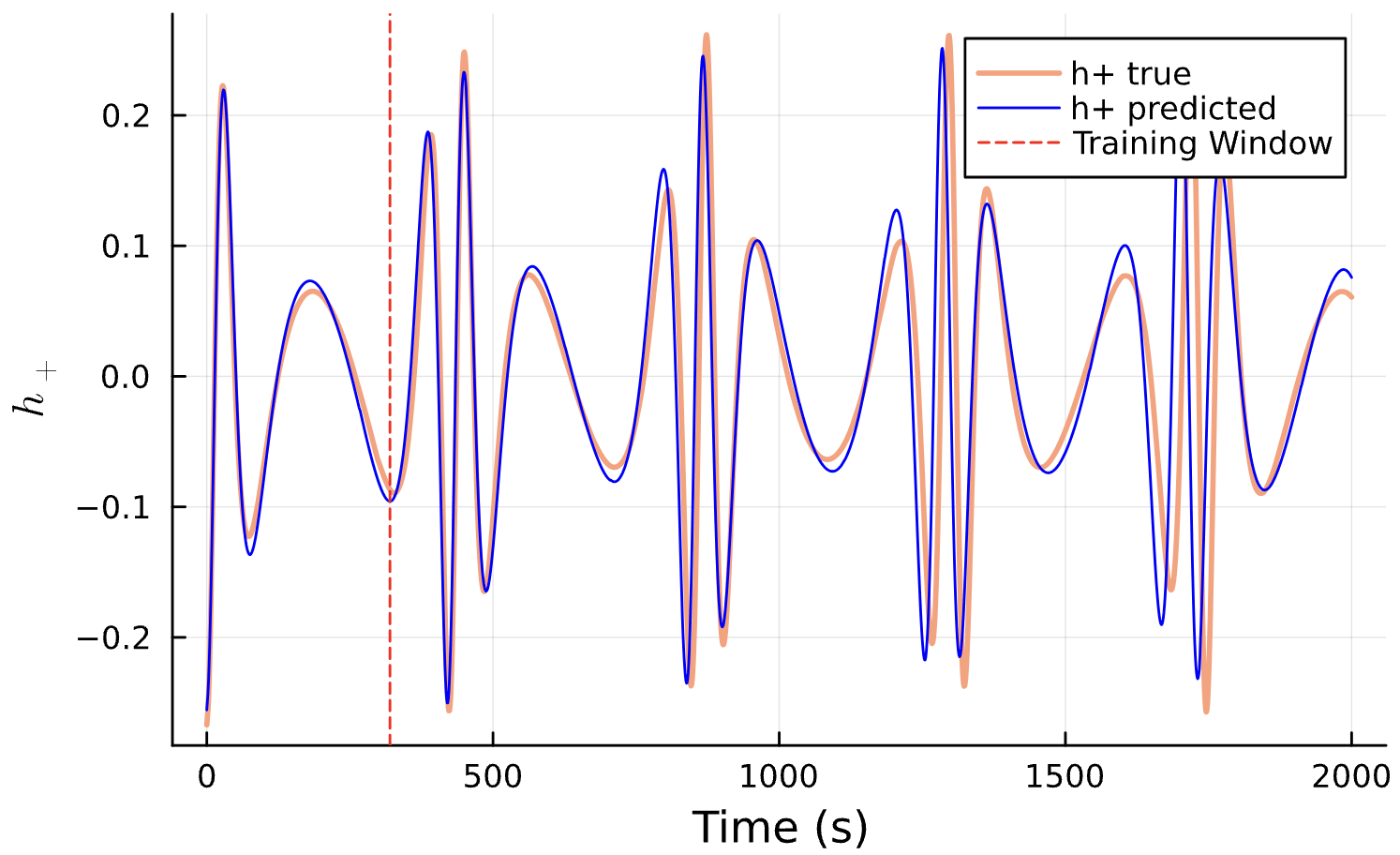
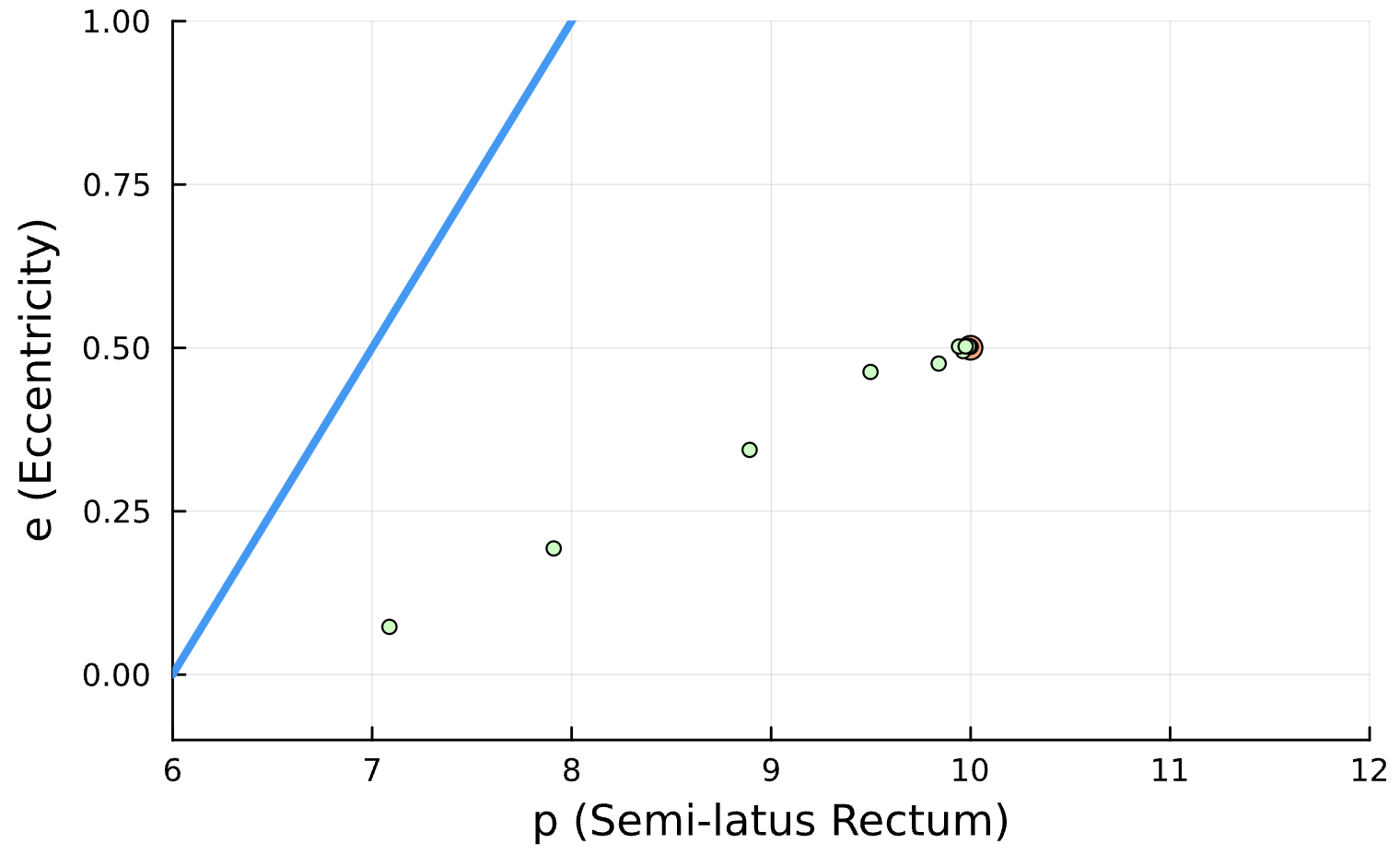

The Goal

The Goal
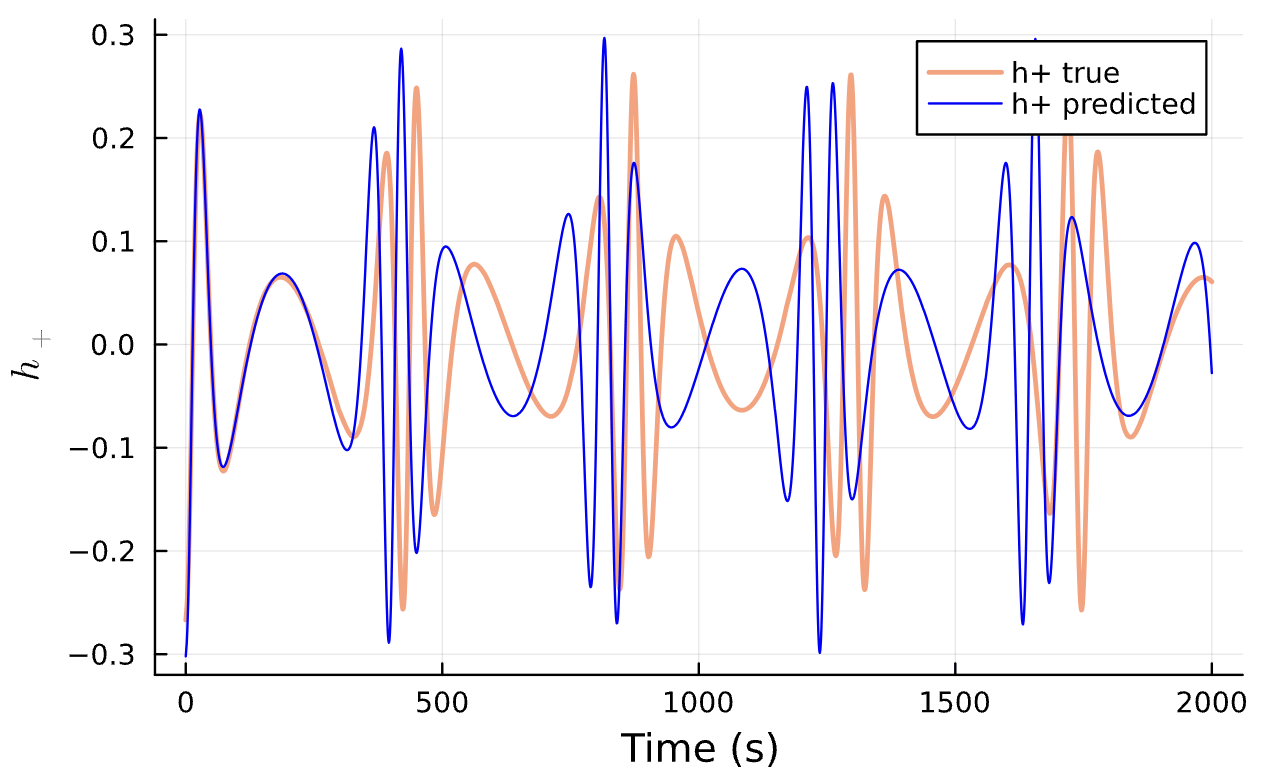
Learned Corrections

The Goal
Conserved Quantities:

Latest Results
Learning Rate = 7e-3, Epochs = 6, # Iterations = 6, Training = 5% ~ 100/2000 time steps
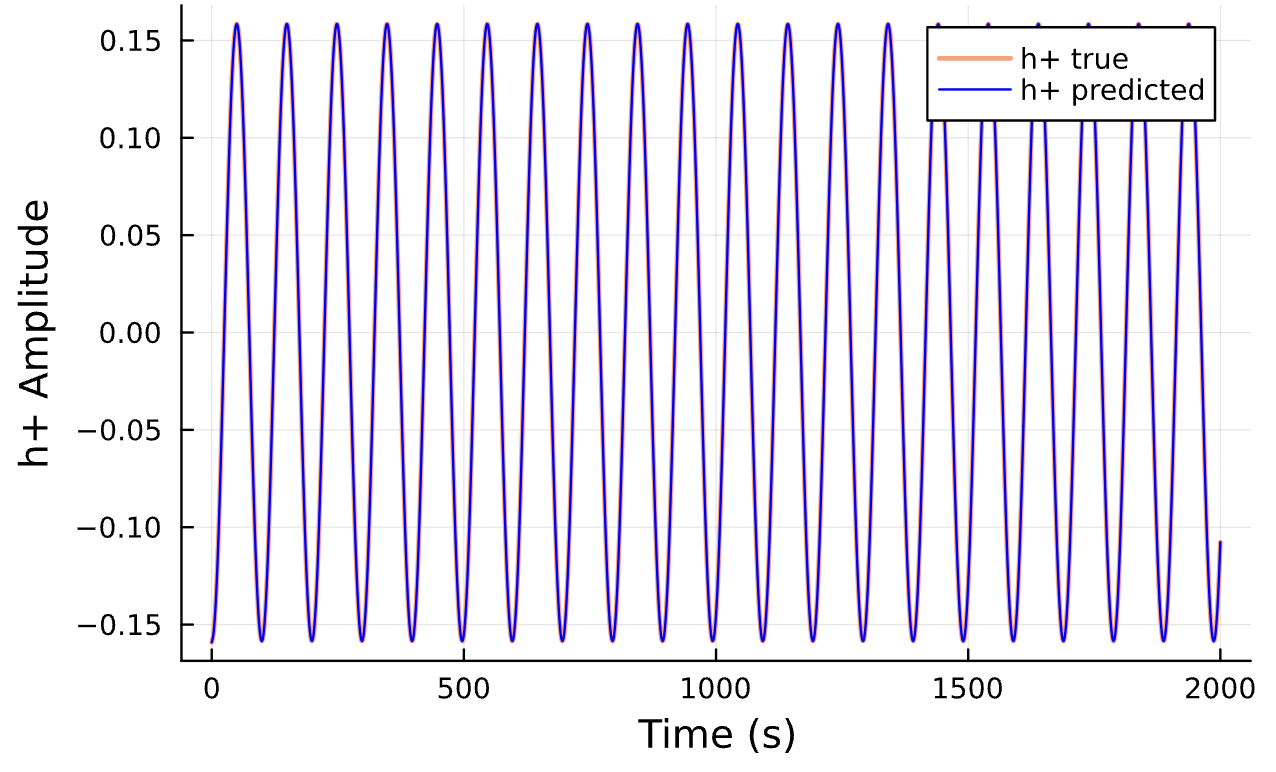

Latest Results
Learning Rate = 1e-2, Epochs = 4, # Iterations = 5, Training = 22% ~ 440/2000 time steps

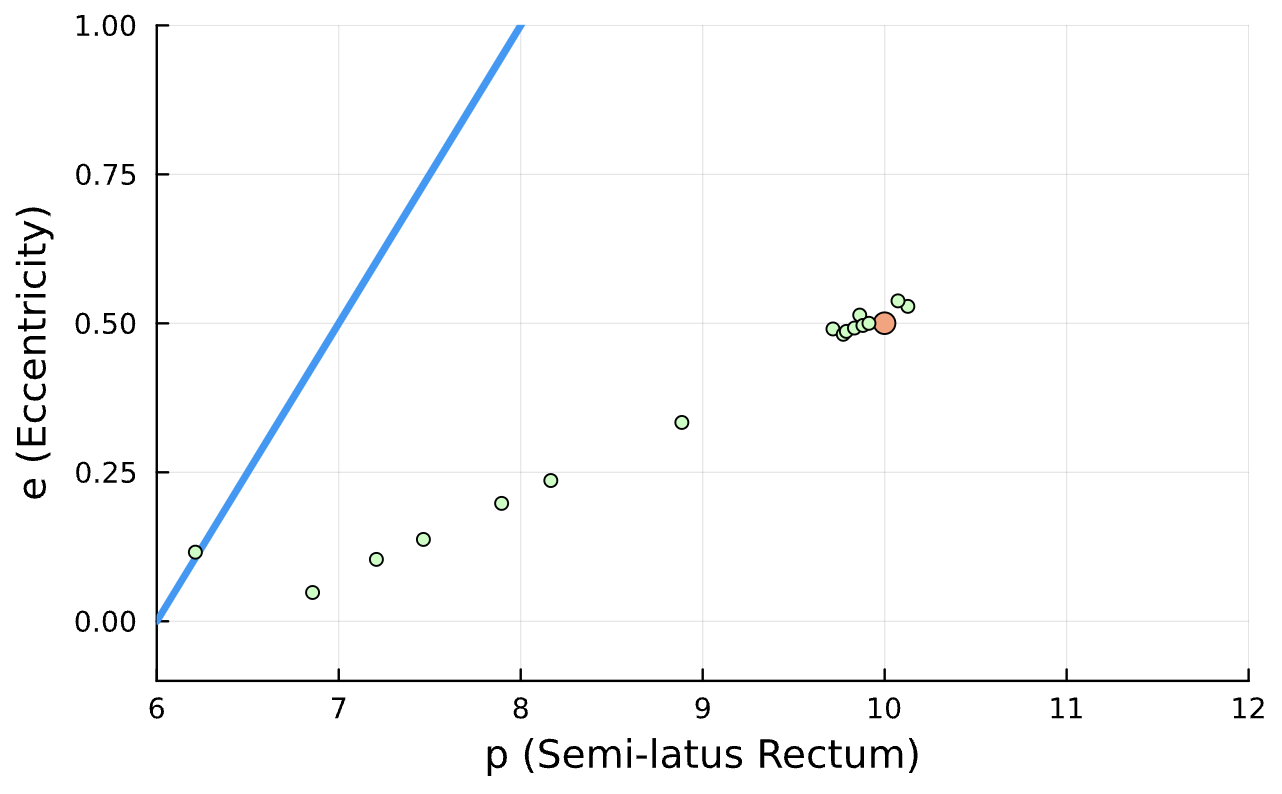
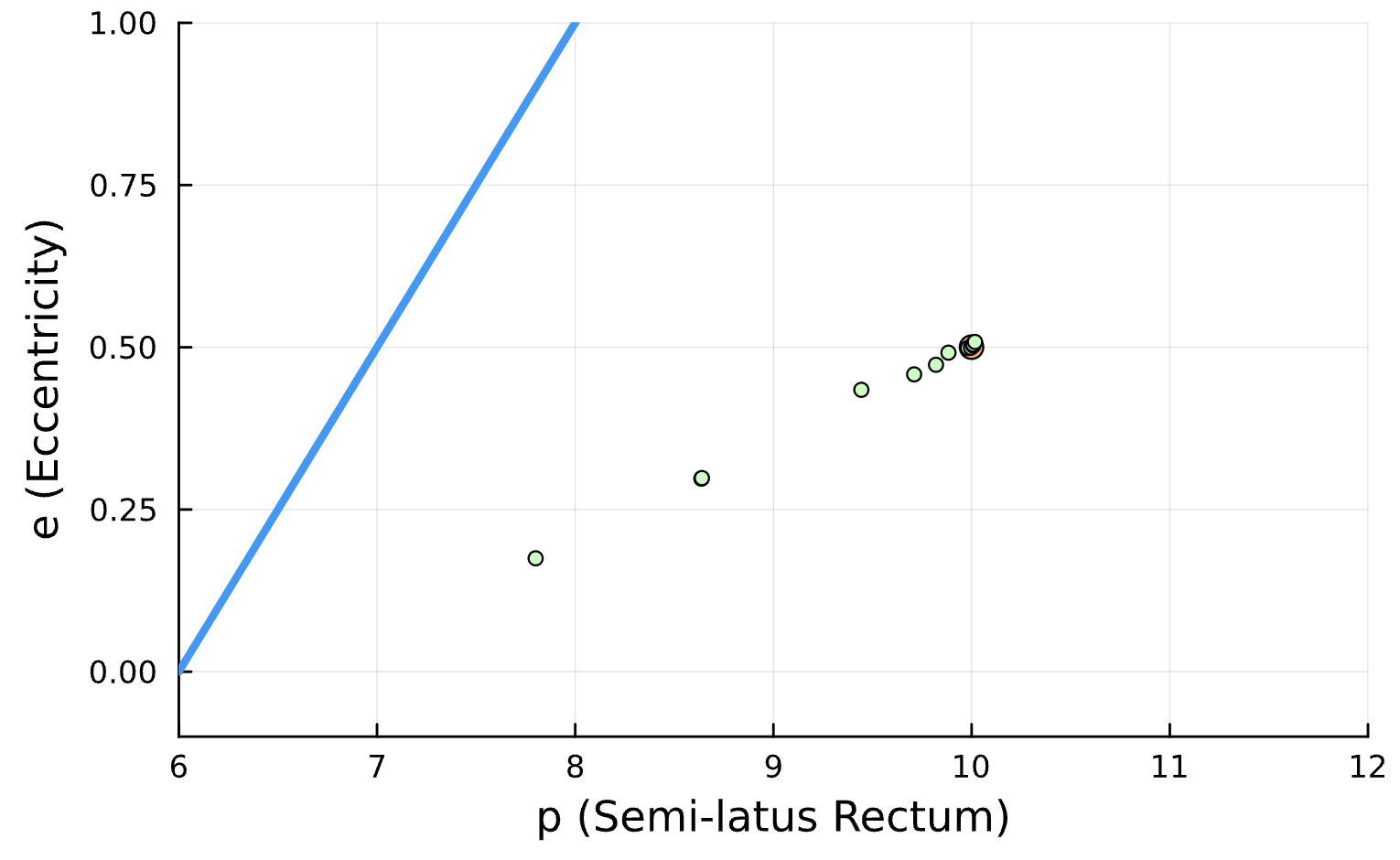
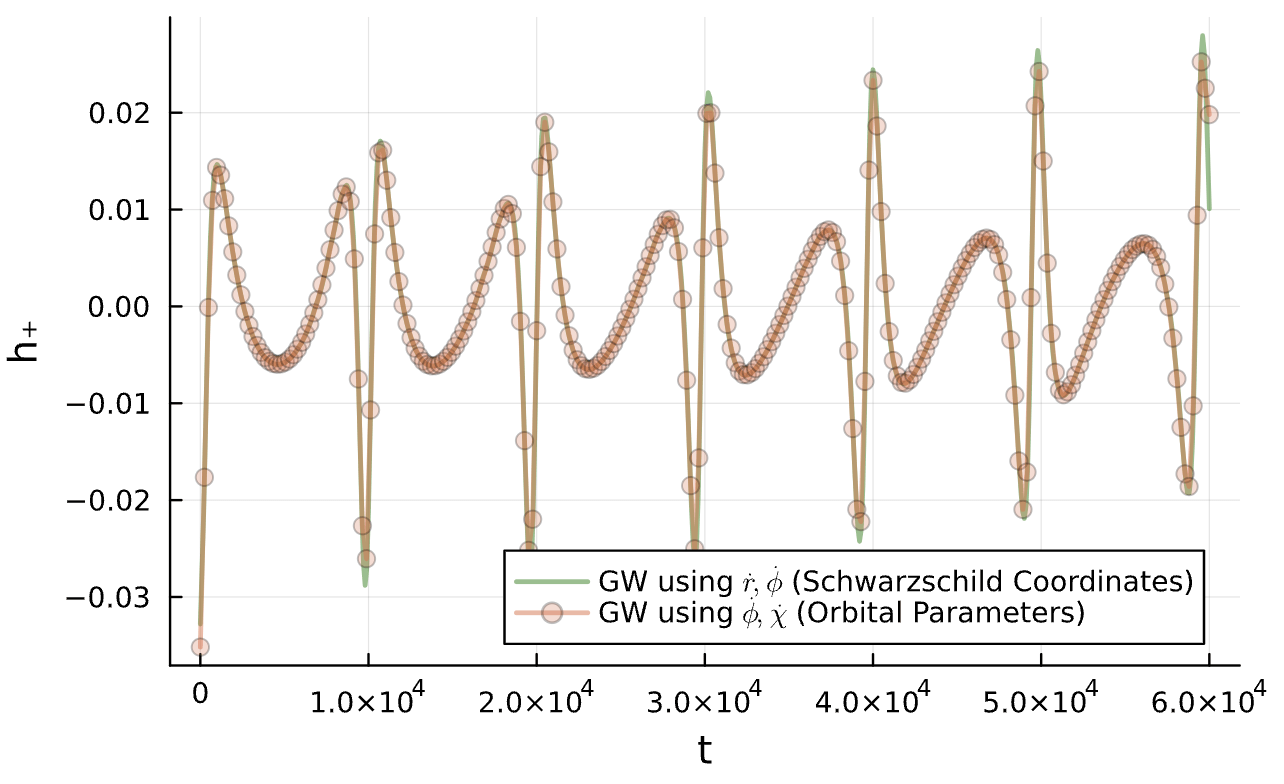
Sensitive!

The Steps
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?

The Steps
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
Yes (thankfully)
Yes (unfortunately)
Yes (no further comment)
Yes (duh)

Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?

Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
M, E, L = p
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
f = (1 - ((2*M)/r))
H_schwarzschild = 1/2 * ( - f^(-1) * (p_t)^2
+ f * (p_r)^2 + (p_φ)^2/r^2 )
return H_schwarzschild
end
# Compute gradient using ForwardDiff
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix J (8x8) -- L is taken!
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
t_val, r_val = x[1], x[2]
f_val = 1 - 2*M/r_val
dτ_dt = f_val/E
du .= du_dτ .* dτ_dt
end
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
M, E, L = p
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_schwarzschild = H(u)
return H_schwarzschild
end
# Compute gradient using ForwardDiff
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix J (8x8)
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
t_val, r_val = x[1], x[2]
f_val = 1 - 2*M/r_val
dτ_dt = f_val/E
du .= du_dτ .* dτ_dt
end
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
M, E, L = p
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_schwarzschild = H(u)
return H_schwarzschild
end
# Compute gradient using ForwardDiff
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix J (8x8)
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
t_val, r_val = x[1], x[2]
f_val = 1 - 2*M/r_val
dτ_dt = f_val/E
du .= du_dτ .* dτ_dt
end
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
M, E, L = p
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_schwarzschild = H(u)
return H_schwarzschild
end
# Compute gradient using ForwardDiff
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix J (8x8)
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
t_val, r_val = x[1], x[2]
f_val = 1 - 2*M/r_val
dτ_dt = f_val/E
du .= du_dτ .* dτ_dt
end
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
M, E, L = p
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_schwarzschild = H(u)
return H_schwarzschild
end
# Compute gradient using ForwardDiff
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix J (8x8)
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
t_val, r_val = x[1], x[2]
f_val = 1 - 2*M/r_val
dτ_dt = f_val/E
du .= du_dτ .* dτ_dt
end
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
M, E, L = p
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_schwarzschild = H(u)
return H_schwarzschild
end
# Compute gradient using ForwardDiff
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix J (8x8)
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
t_val, r_val = x[1], x[2]
f_val = 1 - 2*M/r_val
dτ_dt = f_val/E
du .= du_dτ .* dτ_dt
end
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u # u[1] = t, u[2] = r, u[3] = θ, u[4] = ϕ
M, E, L = p
function H(state_vec)
t, r, θ, φ, p_t, p_r, p_θ, p_φ = state_vec
H_schwarzschild = H(u)
return H_schwarzschild
end
# Compute gradient using ForwardDiff
grad_H = ForwardDiff.gradient(H, x)
# Define antisymmetric matrix J (8x8)
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
t_val, r_val = x[1], x[2]
f_val = 1 - 2*M/r_val
dτ_dt = f_val/E
du .= du_dτ .* dτ_dt
end
The Steps
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?

Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
function SchwarzschildHamiltonian_GENERIC(du, u, p, t)
x = u
NN_params = p.NN
M, E, L = p.parameters.M, p.parameters.E, p.parameters.L
function H(state_vec)
define state_vector
define H_kepler
define NN_correction
return H_kepler + NN_correction
end
# Compute gradient using ForwardDiff
grad_H = ForwardDiff.gradient(H, x)
# Define symplectic matrix L (8x8)
J = [zeros(4,4) I(4);
-I(4) zeros(4,4)]
# Hamilton's equations: ẋ = J*∇H
du_dτ = J * grad_H
t_val, r_val = x[1], x[2]
f_val = 1 - 2*M/r_val
dτ_dt = f_val/E
du .= du_dτ .* dτ_dt
end
The Steps
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?

Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
using hyperopt
function objective_function(lr, epochs, numCycles, train%)
parameter_error = optimizeBlackHole(learningRate = learningRate,
epochsPerIteration = epochsPerIteration,
numberOfCycles = numberOfCycles,
totalTrainingPercent = totalTrainingPercent,
true_parameters = [10, 0.2],
initial_guess = [10, 0.2])
println("lr=$learningRate, epochs=$epochsPerIteration → error=$parameter_error")
return parameter_error
end
ho = @hyperopt for i=20,
learningRate = [1e-3, 3e-3, 6e-3, 1e-2, 2e-2],
epochsPerIteration = [2, 5, 10, 20, 50],
numberOfCycles = [3, 5, 7, 10, 15],
totalTrainingPercent = [0.1, 0.2, 0.3, 0.5, 0.7]
objective_function(learningRate, epochsPerIteration,
numberOfCycles, totalTrainingPercent)
endLearning Rate = 6e-3, Epochs = 10
# Iterations = 15, Training = 20%

Base Model
Does the base model even matter?
What are the optimal hyperparameters?
Do we have to be careful with proper v. coordinate time?
Does my training data match the 2021 paper's training data?
complexity

Base Model
Does the base model even matter?
complexity