Binary Black Holes
A GENERIC Approach
Ref Bari
Advisor: Prof. Brendan Keith


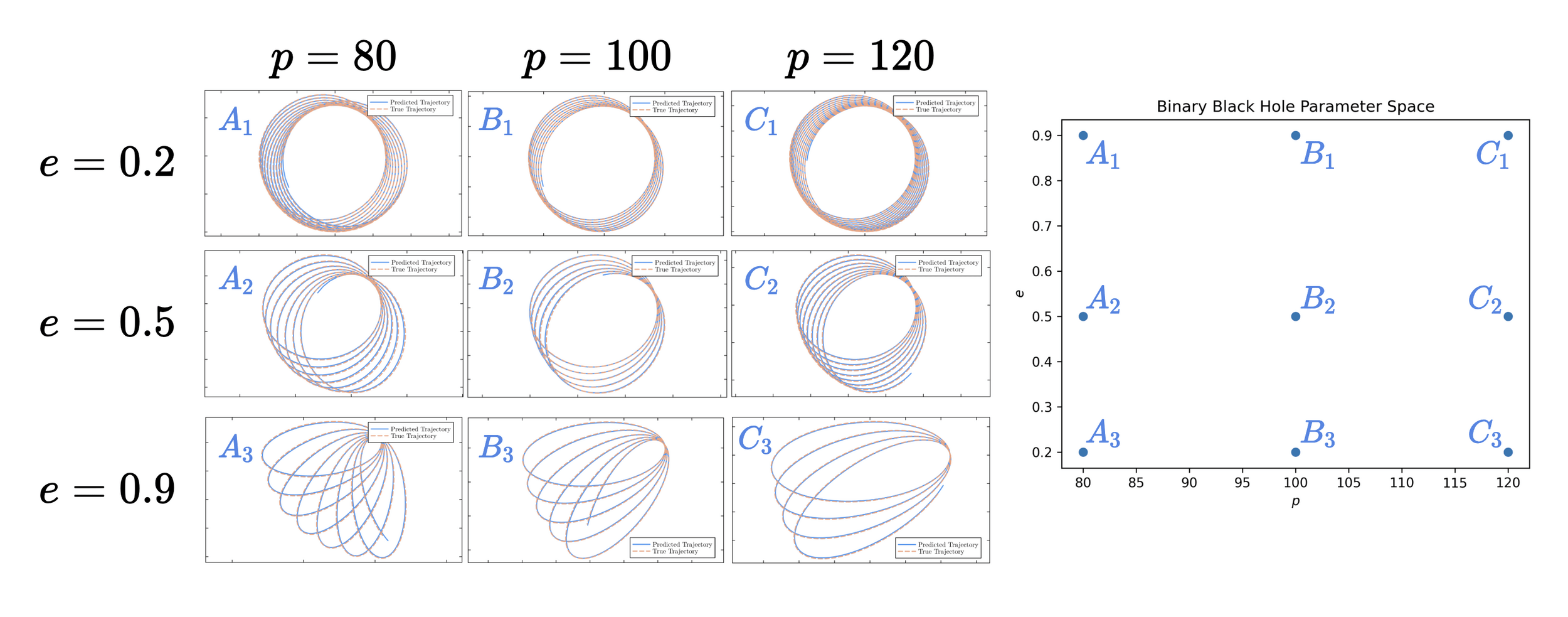

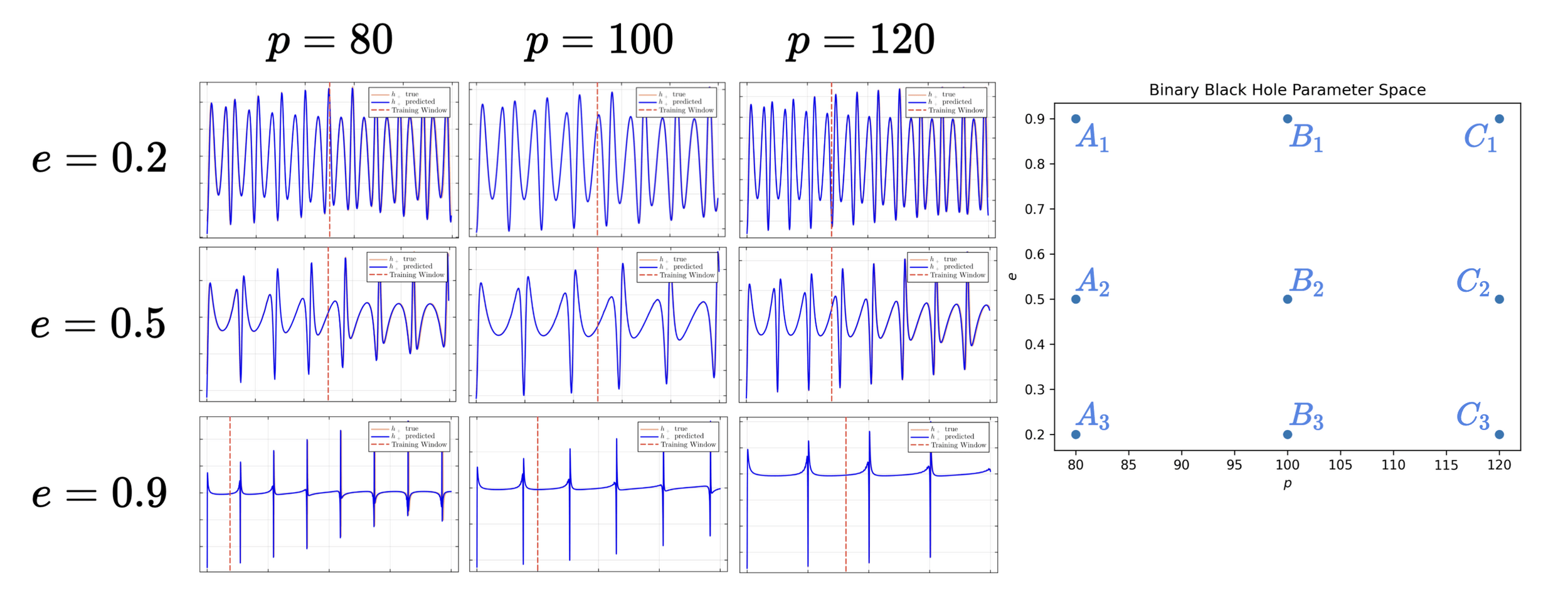


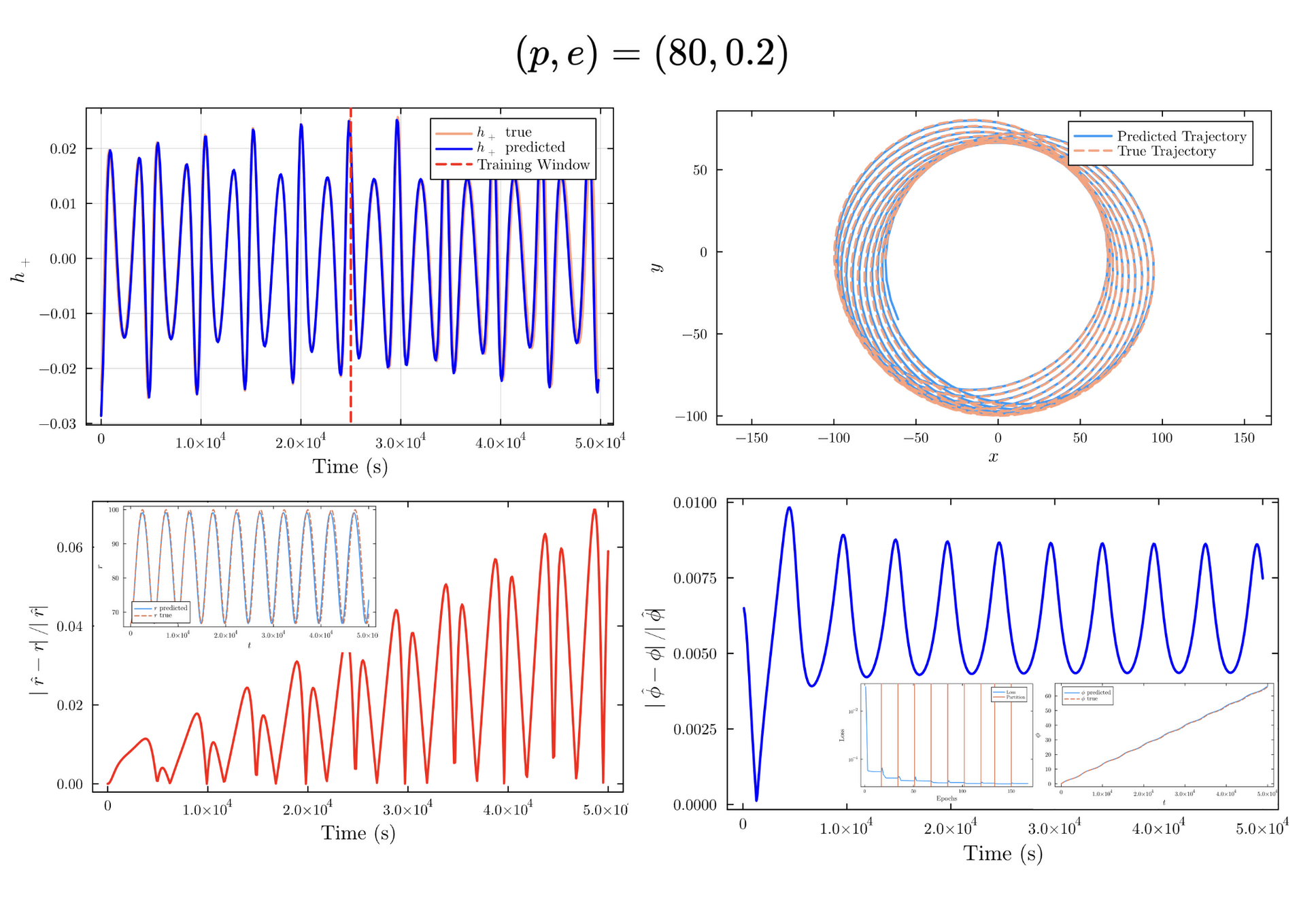
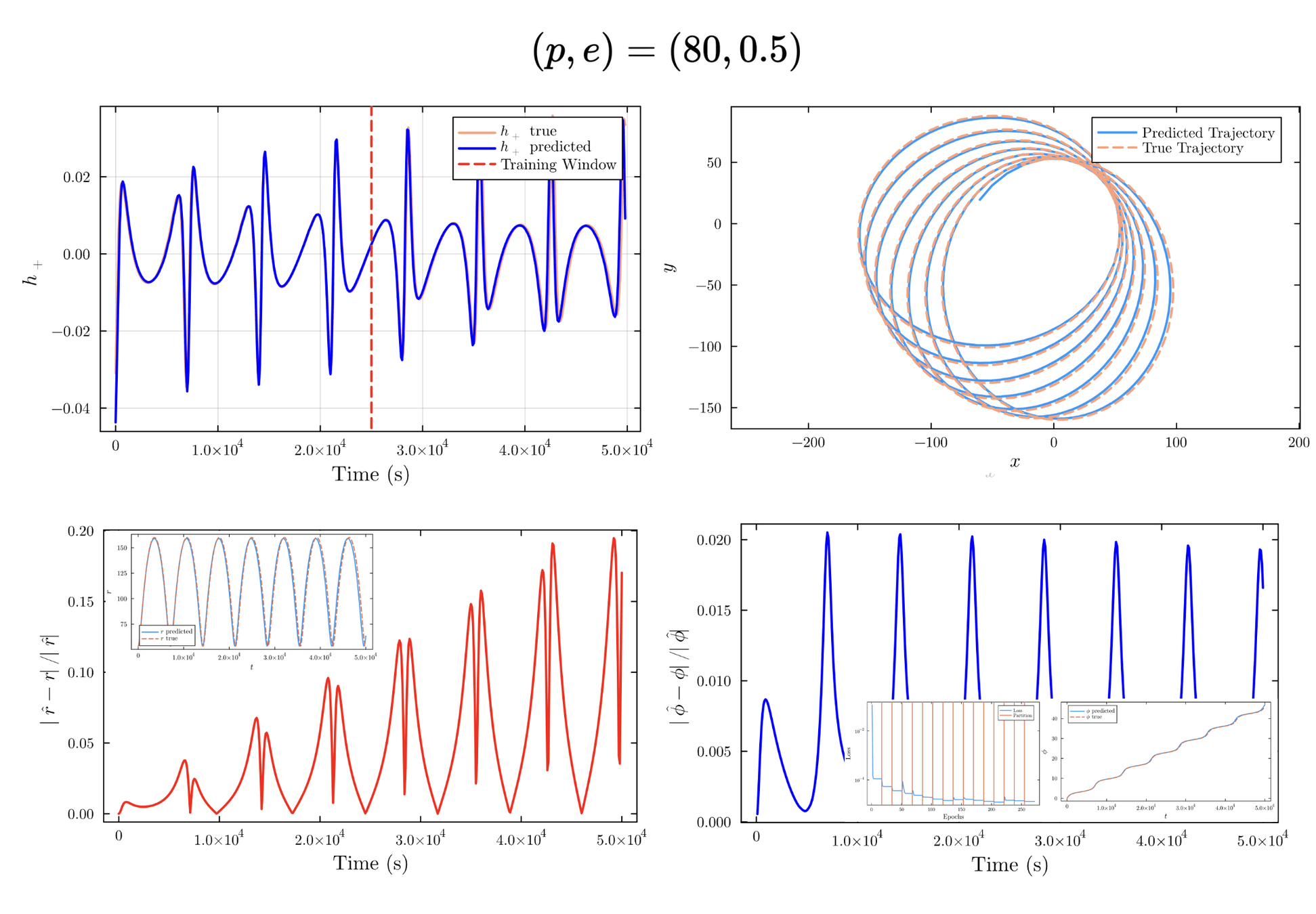














L_2 = \sum |h-\hat h|^2 + |\dot h - \dot{\hat{h}}|^2
L_2 = \sum |h-\hat h|^2






Neural ODE
Training Data
ODE Solver
BFGS Optimizer
g_{\text{Newtonian}}
g_{\text{Schwarzschild}}
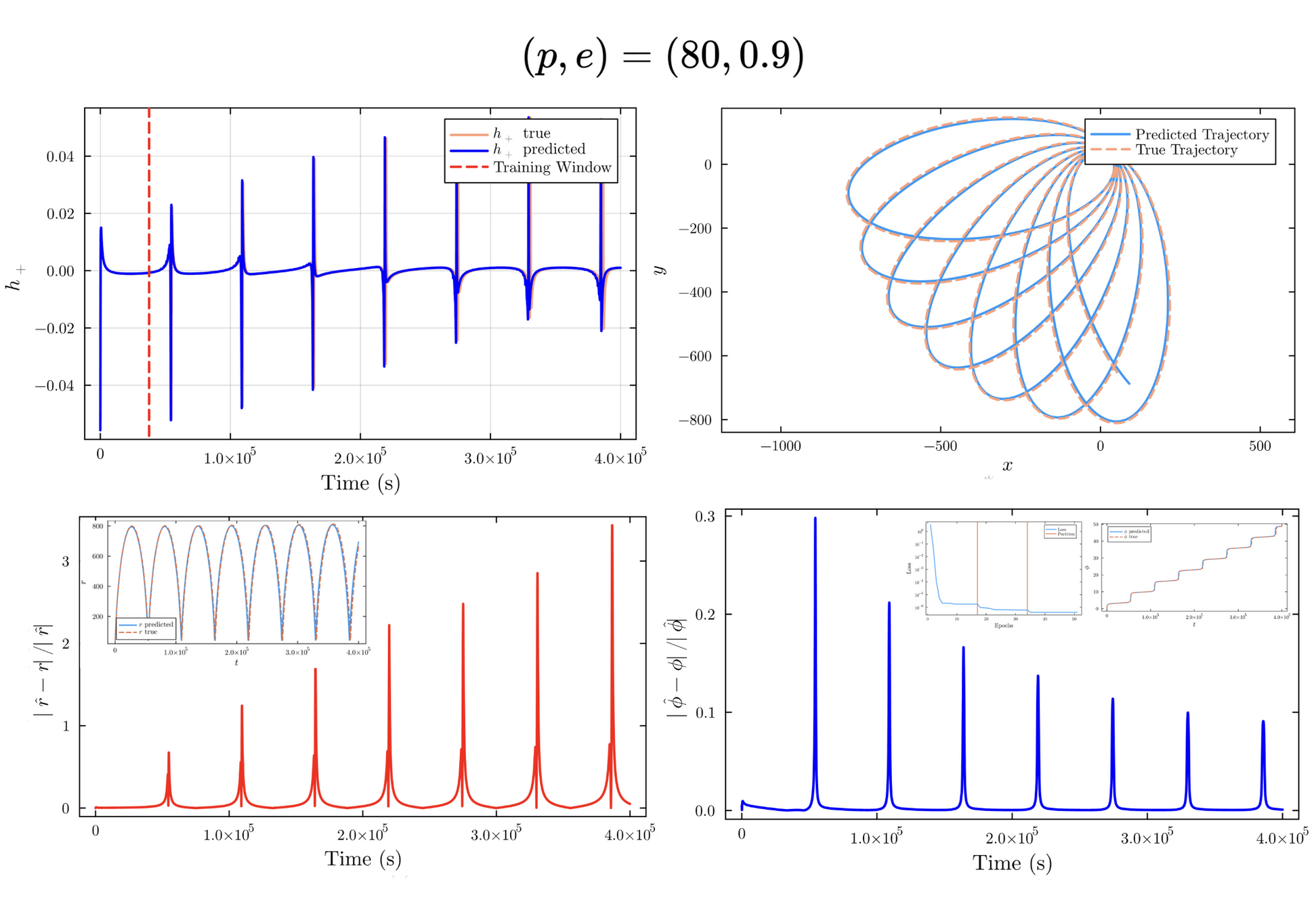
Neural ODE:
Training Data:
H_{pred} = \frac{1}{2}p^T g_{pred} p = \frac{1}{2}p^T [g_{Newton}+f_{NN}] p \to \dot x = L\nabla H_{pred}
ODE Solver:
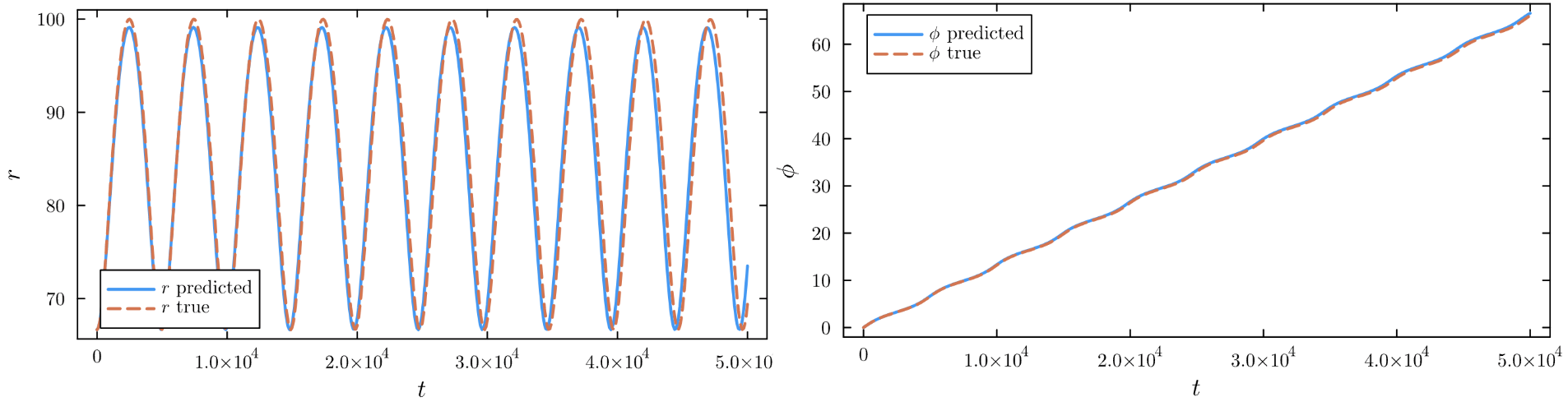
u(t) = [t(t), r(t), \theta(t), \phi(t), p_t(t), p_r(t), p_\theta(t), p_\phi(t)]
(r(t), \phi(t)) \to (x(t), y(t)) \to h(t)
BFGS Optimizer:
\begin{align*}\text{min}_{\eta} \sum &(h_{pred}-h_{true})^2 \\+ &(\dot h_{pred}-\dot h_{true})^2+ (\ddot h_{pred}-\ddot h_{true})^2\end{align*}
\frac{du}{d\tau} = L \nabla H_{Schwarzschild} \to \frac{du}{dt} = \frac{du}{d\tau}\frac{d\tau}{dt} \to u(t) \to h(t)
g_{\text{Newtonian}}=\begin{pmatrix}
-(1+2\phi) & 0 & 0 & 0\\
0 & (1-2\phi) & 0 & 0\\
0 & 0 & r^{2}(1-2\phi) & 0 \\
0 & 0 & 0 & r^{2}(1-2\phi)
\end{pmatrix}
g_{\text{Schwarzschild}} = \begin{pmatrix}
-\left(1-\frac{2M}{r} \right) & 0 & 0 & 0 \\
0 & \left(1-\frac{2M}{r} \right)^{-1} & 0 & 0 \\
0 & 0 & r^2 & 0 \\
0 & 0 & 0 & r^2
\end{pmatrix}
g_{\text{Newtonian}}=\begin{pmatrix}
-(1+2\phi) & 0 & 0 & 0\\
0 & (1-2\phi) & 0 & 0\\
0 & 0 & r^{2}(1-2\phi) & 0 \\
0 & 0 & 0 & r^{2}(1-2\phi)
\end{pmatrix}
g_{\text{Newtonian}}=\begin{pmatrix}
-(1+2\phi) & 0 & 0 & 0\\
0 & (1-2\phi) & 0 & 0\\
0 & 0 & r^{2}(1-2\phi) & 0 \\
0 & 0 & 0 & r^{2}(1-2\phi)
\end{pmatrix}
g_{\text{Newtonian}}=\begin{pmatrix}
-(1+2\phi) & 0 & 0 & 0\\
0 & (1-2\phi) & 0 & 0\\
0 & 0 & r^{2}(1-2\phi) & 0 \\
0 & 0 & 0 & r^{2}(1-2\phi)
\end{pmatrix}
\phi = -\frac{GM}{r}\to\phi =-\frac{1}{r}
g_{\text{Newtonian}}=\begin{pmatrix}
-(1-\frac{2}{r}) & 0 & 0 & 0\\
0 & (1+\frac{2}{r}) & 0 & 0\\
0 & 0 & r^{2}(1+\frac{2}{r}) & 0 \\
0 & 0 & 0 & r^{2}(1+\frac{2}{r})
\end{pmatrix}
g_{\text{Newtonian}}=\begin{pmatrix}
-(1-\frac{2}{r}) & 0 & 0 & 0\\
0 & (1+\frac{2}{r}) & 0 & 0\\
0 & 0 & r^{2}(1+\frac{2}{r}) & 0 \\
0 & 0 & 0 & r^{2}(1+\frac{2}{r})
\end{pmatrix}
g_{\text{Newtonian}}=\begin{pmatrix}
-(1-\frac{2}{r}) & 0 & 0 & 0\\
0 & (1+\frac{2}{r}) & 0 & 0\\
0 & 0 & r^{2}(1+\frac{2}{r}) & 0 \\
0 & 0 & 0 & r^{2}(1+\frac{2}{r})
\end{pmatrix}
\nabla_p p=0
g_{\text{Newtonian}}=\begin{pmatrix}
-(1-\frac{2}{r}) & 0 & 0 & 0\\
0 & (1+\frac{2}{r}) & 0 & 0\\
0 & 0 & r^{2}(1+\frac{2}{r}) & 0 \\
0 & 0 & 0 & r^{2}(1+\frac{2}{r})
\end{pmatrix}
\nabla_p p=0
\mu = 0
\mu = i
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^0+\Gamma_{\alpha \beta}^0 p^\alpha p^\beta=0
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^i+\Gamma_{\alpha \beta}^i p^\alpha p^\beta=0
g_{\text{Newtonian}}=\begin{pmatrix}
-(1-\frac{2}{r}) & 0 & 0 & 0\\
0 & (1+\frac{2}{r}) & 0 & 0\\
0 & 0 & r^{2}(1+\frac{2}{r}) & 0 \\
0 & 0 & 0 & r^{2}(1+\frac{2}{r})
\end{pmatrix}
\nabla_p p=0
\mu = 0
\mu = i
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^0+\Gamma_{\alpha \beta}^0 p^\alpha p^\beta=0
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^i+\Gamma_{\alpha \beta}^i p^\alpha p^\beta=0
\begin{aligned} \Gamma_{00}^0 & =\frac{1}{2} g^{00} g_{00,0} =\phi_{, 0}+0\left(\phi^2\right) \end{aligned}
\begin{aligned} \Gamma_{00}^i & =-\frac{1}{2} g_{00, j} \delta^{i j} =-\frac{1}{2}(-2 \phi)_j \delta^{i j} \end{aligned}
g_{\text{Newtonian}}=\begin{pmatrix}
-(1-\frac{2}{r}) & 0 & 0 & 0\\
0 & (1+\frac{2}{r}) & 0 & 0\\
0 & 0 & r^{2}(1+\frac{2}{r}) & 0 \\
0 & 0 & 0 & r^{2}(1+\frac{2}{r})
\end{pmatrix}
\nabla_p p=0
\mu = 0
\mu = i
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^0+\Gamma_{\alpha \beta}^0 p^\alpha p^\beta=0
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^i+\Gamma_{\alpha \beta}^i p^\alpha p^\beta=0
\begin{aligned} \Gamma_{00}^0 & =\frac{1}{2} g^{00} g_{00,0} =\phi_{, 0}+0\left(\phi^2\right) \end{aligned}
\begin{aligned} \Gamma_{00}^i & =-\frac{1}{2} g_{00, j} \delta^{i j} =-\frac{1}{2}(-2 \phi)_j \delta^{i j} \end{aligned}
\frac{\mathrm{d}}{\mathrm{d} \tau} p^0=-m \frac{\partial \phi}{\partial \tau}
\frac{d}{d\tau}p^i=-m \phi_j \delta^{i j}
g_{\text{Newtonian}}=\begin{pmatrix}
-(1-\frac{2}{r}) & 0 & 0 & 0\\
0 & (1+\frac{2}{r}) & 0 & 0\\
0 & 0 & r^{2}(1+\frac{2}{r}) & 0 \\
0 & 0 & 0 & r^{2}(1+\frac{2}{r})
\end{pmatrix}
\nabla_p p=0
\mu = 0
\mu = i
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^0+\Gamma_{\alpha \beta}^0 p^\alpha p^\beta=0
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^i+\Gamma_{\alpha \beta}^i p^\alpha p^\beta=0
\begin{aligned} \Gamma_{00}^0 & =\frac{1}{2} g^{00} g_{00,0} =\phi_{, 0}+0\left(\phi^2\right) \end{aligned}
\begin{aligned} \Gamma_{00}^i & =-\frac{1}{2} g_{00, j} \delta^{i j} =-\frac{1}{2}(-2 \phi)_j \delta^{i j} \end{aligned}
\frac{\mathrm{d}}{\mathrm{d} \tau} p^0=-m \frac{\partial \phi}{\partial \tau}
\frac{d}{d\tau}p^i=-m \phi_j \delta^{i j}
g_{\text{Newtonian}}=\begin{pmatrix}
-(1-\frac{2}{r}) & 0 & 0 & 0\\
0 & (1+\frac{2}{r}) & 0 & 0\\
0 & 0 & r^{2}(1+\frac{2}{r}) & 0 \\
0 & 0 & 0 & r^{2}(1+\frac{2}{r})
\end{pmatrix}
\nabla_p p=0
\mu = 0
\mu = i
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^0+\Gamma_{\alpha \beta}^0 p^\alpha p^\beta=0
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^i+\Gamma_{\alpha \beta}^i p^\alpha p^\beta=0
\begin{aligned} \Gamma_{00}^0 & =\frac{1}{2} g^{00} g_{00,0} =\phi_{, 0}+0\left(\phi^2\right) \end{aligned}
\begin{aligned} \Gamma_{00}^i & =-\frac{1}{2} g_{00, j} \delta^{i j} =-\frac{1}{2}(-2 \phi)_j \delta^{i j} \end{aligned}
\dot E = 0
F=ma
g_{\text{Newtonian}}=\begin{pmatrix}
-(1-\frac{2}{r}) & 0 & 0 & 0\\
0 & (1+\frac{2}{r}) & 0 & 0\\
0 & 0 & r^{2}(1+\frac{2}{r}) & 0 \\
0 & 0 & 0 & r^{2}(1+\frac{2}{r})
\end{pmatrix}
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^0+\Gamma_{\alpha \beta}^0 p^\alpha p^\beta=0
m \frac{\mathrm{~d}}{\mathrm{~d} \tau} p^i+\Gamma_{\alpha \beta}^i p^\alpha p^\beta=0
\begin{aligned} \Gamma_{00}^0 & =\frac{1}{2} g^{00} g_{00,0} =\phi_{, 0}+0\left(\phi^2\right) \end{aligned}
\begin{aligned} \Gamma_{00}^i & =-\frac{1}{2} g_{00, j} \delta^{i j} =-\frac{1}{2}(-2 \phi)_j \delta^{i j} \end{aligned}
g_{\text{Schwarzschild}} = \begin{pmatrix}
-\left(1-\frac{2}{r} \right) & 0 & 0 & 0 \\
0 & \left(1-\frac{2}{r} \right)^{-1} & 0 & 0 \\
0 & 0 & r^2 & 0 \\
0 & 0 & 0 & r^2
\end{pmatrix}