Binary Black Holes
A GENERIC Approach
Ref Bari
Advisor: Prof. Brendan Keith


Introduction to GENERIC

dU = {dW} +{dQ}
\dot{x} = \dot{x}_{\text{R}} + \dot{x}_{\text{I}}
Equilibrium
Inequilibrium
dU = {-p dV} +{T dS}
\dot{x} = L \nabla E + M \nabla S
\frac{dU}{dt} = 0
M \nabla E =0
L \nabla S =0
\frac{dS}{dt} \geq 0
L^T=-L
M^T=M, M\geq0
Introduction to GENERIC

\dot{x} = \dot{x}_{\text{R}} + \dot{x}_{\text{I}}
\dot{x} = L \nabla E + M \nabla S
\frac{dE}{dt} = 0
M \nabla E =0
L \nabla S =0
\frac{dS}{dt} \geq 0
L^T=-L
M^T=M, M\geq0
\dot{x} = L \nabla E + M \nabla S
\dot{x} = L \nabla E + M \nabla S
E(x) = H - TS
S(x) = S
\dot{x} = L \nabla E + M \nabla S
E(x) = H - TS \to \dot E=0
S(x) = S\to \dot S\geq 0
S(x) = E_{GW}\to \dot E_{GW}\geq 0
\dot{x} = L \nabla E + M \nabla S
E(x) = H - TS
S(x) = S
L = \begin{pmatrix}
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
-1 & 0 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0
\end{pmatrix}
M = \begin{pmatrix}
M_{11} & M_{12} & M_{13} & M_{14} & M_{15} \\
M_{12} & M_{22} & M_{23} & M_{24} & M_{25} \\
M_{13} & M_{23} & M_{33} & M_{34} & M_{35} \\
M_{14} & M_{24} & M_{34} & M_{44} & M_{45} \\
M_{15} & M_{25} & M_{35} & M_{45} & M_{55}
\end{pmatrix}
\dot{x} = L \nabla E + M \nabla S
E(x) = H - TS
S(x) = S
L = \begin{pmatrix}
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
-1 & 0 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0
\end{pmatrix}
M = \begin{pmatrix}
M_{11} & M_{12} & M_{13} & M_{14} & M_{15} \\
M_{12} & M_{22} & M_{23} & M_{24} & M_{25} \\
M_{13} & M_{23} & M_{33} & M_{34} & M_{35} \\
M_{14} & M_{24} & M_{34} & M_{44} & M_{45} \\
M_{15} & M_{25} & M_{35} & M_{45} & M_{55}
\end{pmatrix}
x = \begin{pmatrix}
r \\
\phi \\
p_r \\
p_\phi \\
S
\end{pmatrix}
\dot{x} = L \nabla E + M \nabla S
E(x) = H - TS \to \nabla E = \begin{pmatrix}
\frac{\partial H}{\partial r},
0,
\frac{\partial H}{\partial p_r},
\frac{\partial H}{\partial p_\phi},
-1
\end{pmatrix}
S(x) = S \to \nabla S = (0, 0, 0, 0, 1)
L = \begin{pmatrix}
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
-1 & 0 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0
\end{pmatrix}
M = \begin{pmatrix}
M_{11} & M_{12} & M_{13} & M_{14} & M_{15} \\
M_{12} & M_{22} & M_{23} & M_{24} & M_{25} \\
M_{13} & M_{23} & M_{33} & M_{34} & M_{35} \\
M_{14} & M_{24} & M_{34} & M_{44} & M_{45} \\
M_{15} & M_{25} & M_{35} & M_{45} & M_{55}
\end{pmatrix}
x = \begin{pmatrix}
r,
\phi,
p_r,
p_\phi,
S
\end{pmatrix}
\dot{x} = L \nabla E + M \nabla S
\begin{pmatrix}
\frac{\partial H}{\partial r}\\
0\\
\frac{\partial H}{\partial p_r}\\
\frac{\partial H}{\partial p_\phi}\\
-1
\end{pmatrix} +
\begin{pmatrix}
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
-1 & 0 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
M_{11} & M_{12} & M_{13} & M_{14} & M_{15} \\
M_{12} & M_{22} & M_{23} & M_{24} & M_{25} \\
M_{13} & M_{23} & M_{33} & M_{34} & M_{35} \\
M_{14} & M_{24} & M_{34} & M_{44} & M_{45} \\
M_{15} & M_{25} & M_{35} & M_{45} & M_{55}
\end{pmatrix}
\dot x = \begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r\\
\dot p_\phi\\
\dot S
\end{pmatrix}=
\begin{pmatrix}0\\ 0\\ 0\\ 0\\ 1\end{pmatrix}
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix} = \begin{pmatrix}
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 \\
-1 & 0 & 0 & 0 & 0 \\
0 & -1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
\frac{\partial H}{\partial r} \\
0 \\
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
1
\end{pmatrix} +
\begin{pmatrix}
M_{11} & M_{12} & M_{13} & M_{14} & M_{15} \\
M_{12} & M_{22} & M_{23} & M_{24} & M_{25} \\
M_{13} & M_{23} & M_{33} & M_{34} & M_{35} \\
M_{14} & M_{24} & M_{34} & M_{44} & M_{45} \\
M_{15} & M_{25} & M_{35} & M_{45} & M_{55}
\end{pmatrix}
\begin{pmatrix}
0 \\
0 \\
0 \\
0 \\
1
\end{pmatrix}
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
M_{15} \\
M_{25} \\
M_{35} \\
M_{45} \\
M_{55}
\end{pmatrix}
M_{i5} \text{ contributes to } \dot x
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
M_{15} \\
M_{25} \\
M_{35} \\
M_{45} \\
M_{55}
\end{pmatrix}
S(x)=-S
E= H-TS
\begin{pmatrix}
M_{11} & M_{12} & M_{13} & M_{14} & M_{15} \\
M_{12} & M_{22} & M_{23} & M_{24} & M_{25} \\
M_{13} & M_{23} & M_{33} & M_{34} & M_{35} \\
M_{14} & M_{24} & M_{34} & M_{44} & M_{45} \\
M_{15} & M_{25} & M_{35} & M_{45} & M_{55}
\end{pmatrix}
\begin{pmatrix}
\frac{\partial H}{\partial r} \\
0 \\
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-1
\end{pmatrix}=
\begin{pmatrix}
0 \\
0 \\
0 \\
0 \\
0
\end{pmatrix}
M_{11}\frac{\partial H}{\partial r}+M_{13}\frac{\partial H}{\partial p_r}+M_{14}\frac{\partial H}{\partial p_\phi}+M_{15}=0
M_{12}\frac{\partial H}{\partial r}+M_{23}\frac{\partial H}{\partial p_r}+M_{24}\frac{\partial H}{\partial p_\phi}+M_{25}=0
M_{13}\frac{\partial H}{\partial r}+M_{33}\frac{\partial H}{\partial p_r}+M_{34}\frac{\partial H}{\partial p_\phi}+M_{35}=0
M_{14}\frac{\partial H}{\partial r}+M_{34}\frac{\partial H}{\partial p_r}+M_{44}\frac{\partial H}{\partial p_\phi}+M_{45}=0
M_{15}\frac{\partial H}{\partial r}+M_{35}\frac{\partial H}{\partial p_r}+M_{45}\frac{\partial H}{\partial p_\phi}-M_{55}=0
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} -
\begin{pmatrix}
0 \\
0\\
0 \\
M_{45} \\
M_{55}
\end{pmatrix}
M_{55}>0
M_{15}=M_{35}=0
M_{45}\frac{\partial H}{\partial p_\phi}-M_{55}=0\to \boxed{M_{45}=\left(\frac{\partial H}{\partial p_\phi} \right)^{-1}M_{55}}
M_{45}>0
M_{55}=1\mathrm{e}{-5}
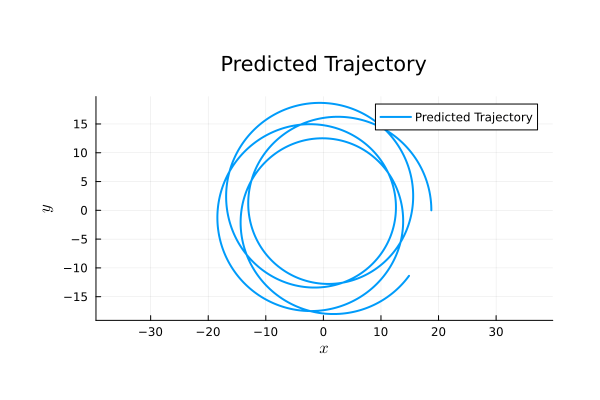
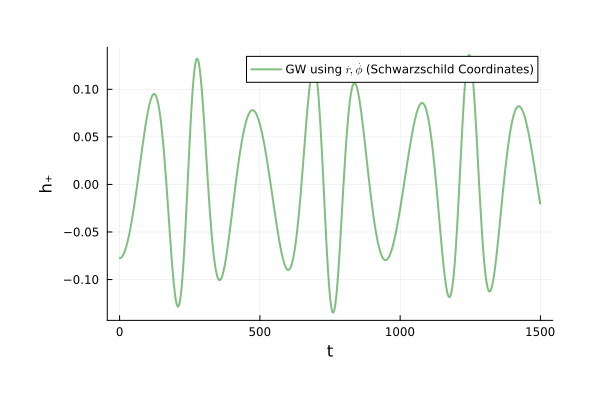
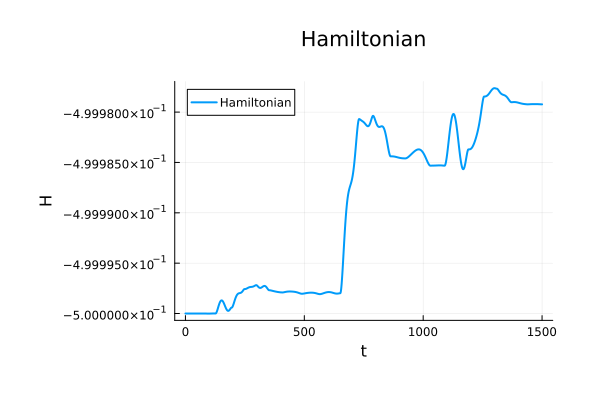
M_{55}=0 \text{ (reference)}

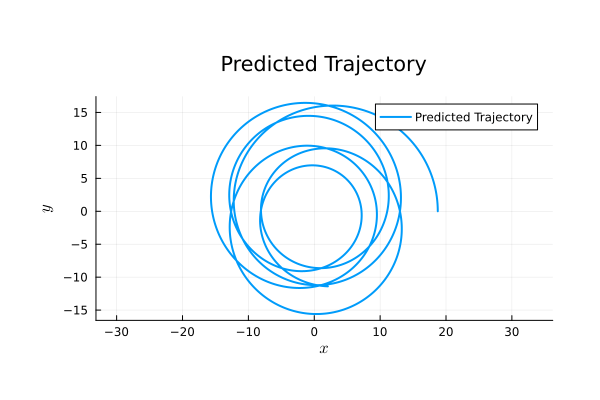
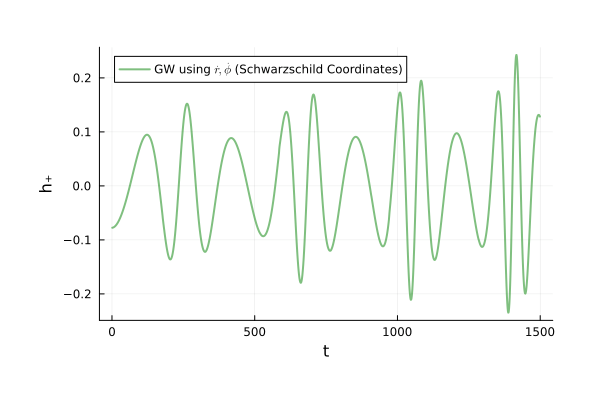
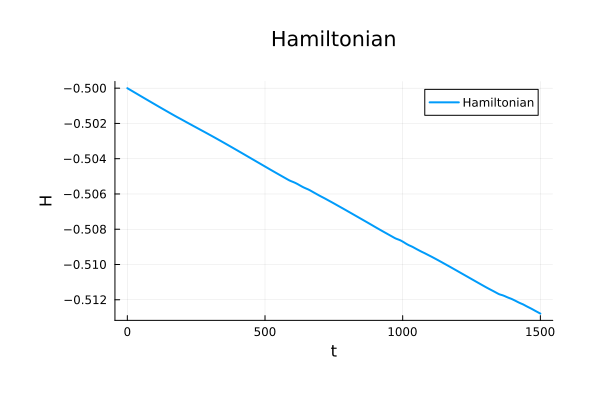
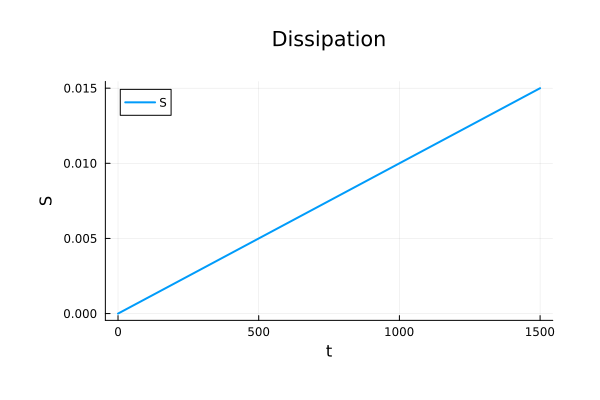
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
0 \\
0\\
M_{35} \\
0 \\
M_{55}
\end{pmatrix}
M_{55}>0
M_{15}=M_{45}=0
M_{35}\neq0
M_{55}=1\mathrm{e}{-7}
M_{55}=0 \text{ (reference)}
M_{35}\frac{\partial H}{\partial p_r}-M_{55}=0 \to \boxed{M_{35} = \left(\frac{\partial H}{\partial p_r} \right)^{-1} M_{55}}
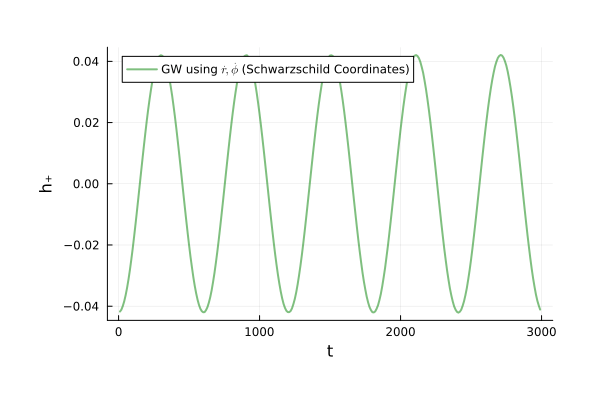
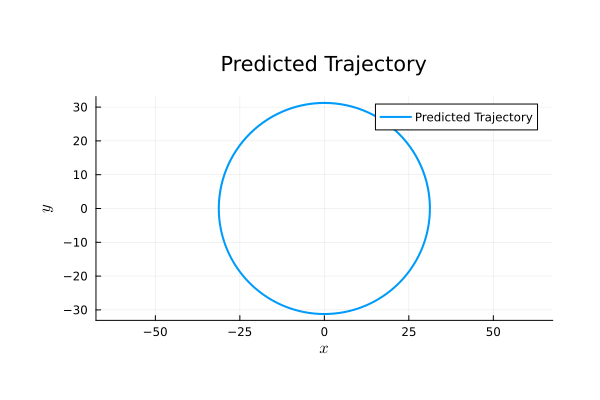
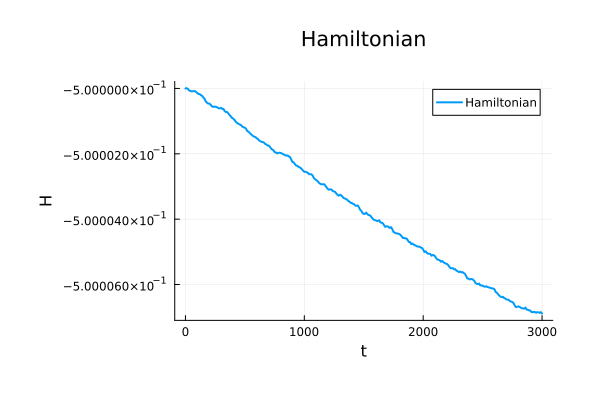
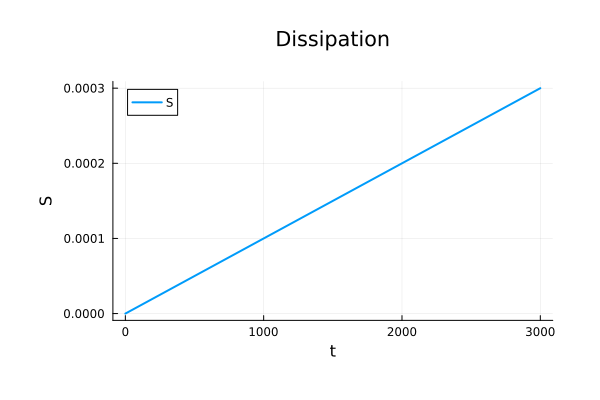
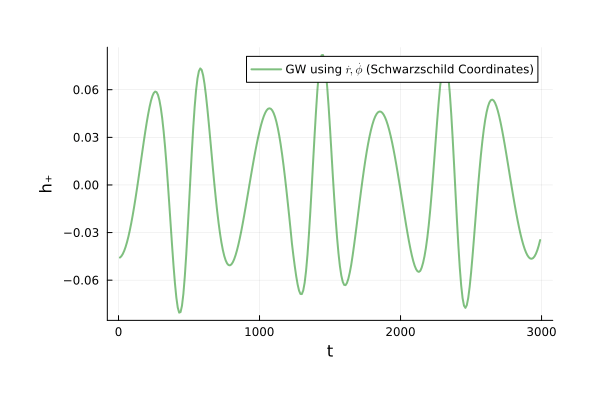
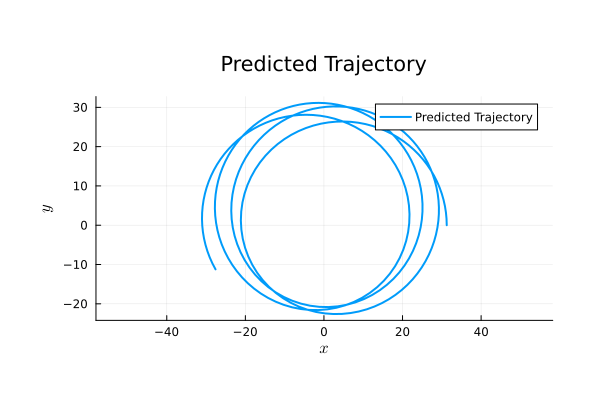
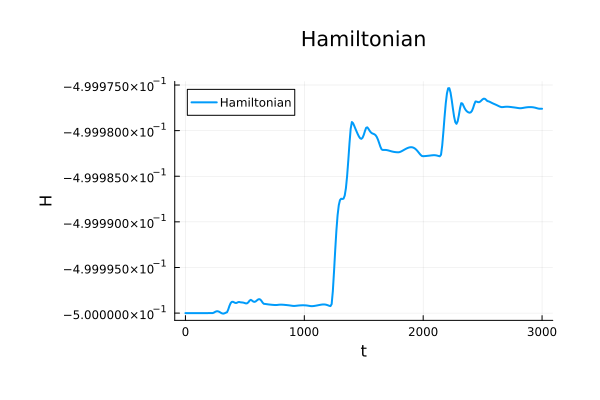
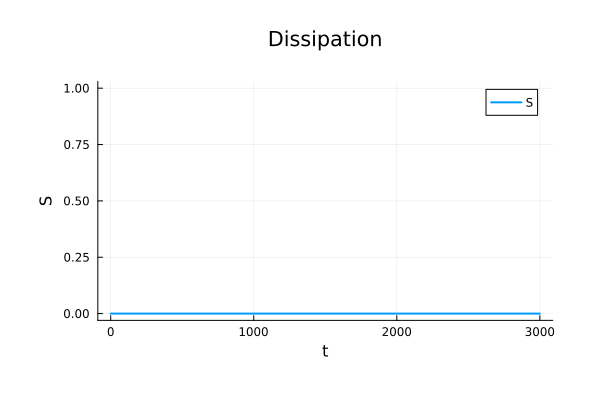
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
M_{15} \\
0\\
0 \\
0 \\
M_{55}
\end{pmatrix}
M_{55}>0
M_{35}=M_{45}=0
M_{15}\neq0
M_{55}=1\mathrm{e}{-6}
M_{55}=0 \text{ (reference)}
M_{15}\frac{\partial H}{\partial r}-M_{55}=0 \to \boxed{M_{15}=\left(\frac{\partial H}{\partial r} \right)^{-1} M_{55}}
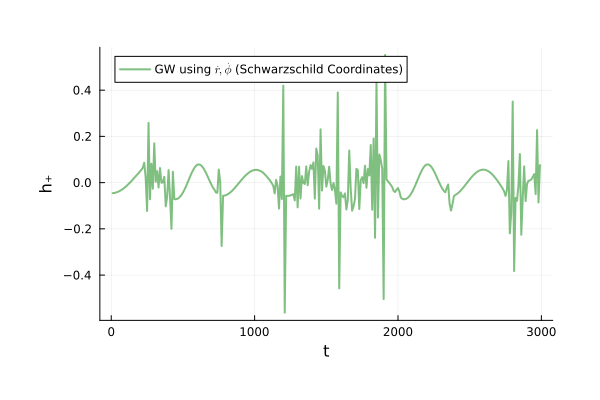
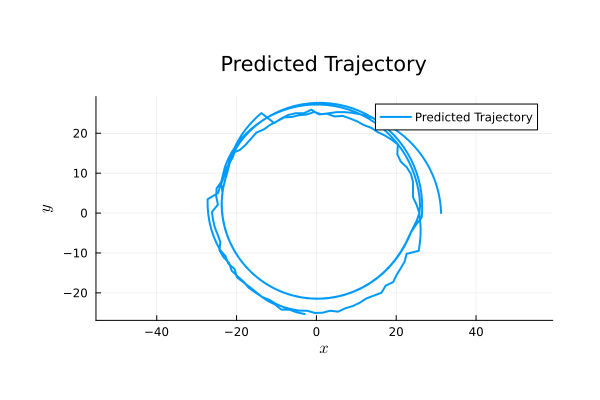
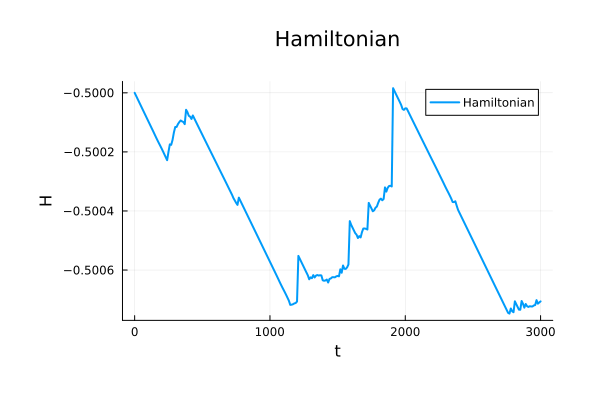
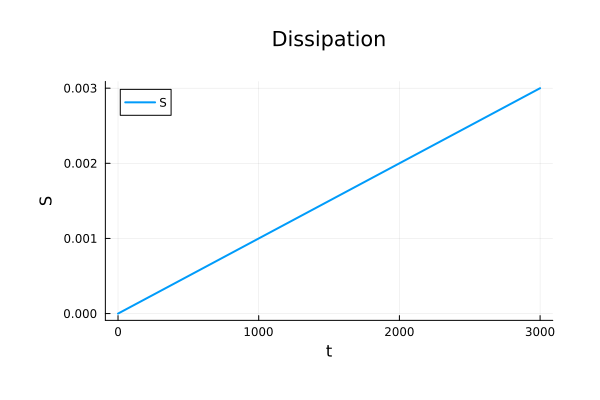




\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} -
\begin{pmatrix}
0 \\
0\\
0 \\
M_{45}(p_\phi, r) \\
M_{55}
\end{pmatrix}
M_{55}>0
M_{15}=M_{35}=0
M_{45}\frac{\partial H}{\partial p_\phi}-M_{55}=0\to \boxed{M_{55}=\left(\frac{\partial H}{\partial p_\phi} \right)M_{45}}
M_{45}>0
M_{55}=1\mathrm{e}{-5}


M_{55}=0 \text{ (reference)}






M\nabla E = 0, L \nabla S = 0
L\nabla E \cdot M \nabla S = 0
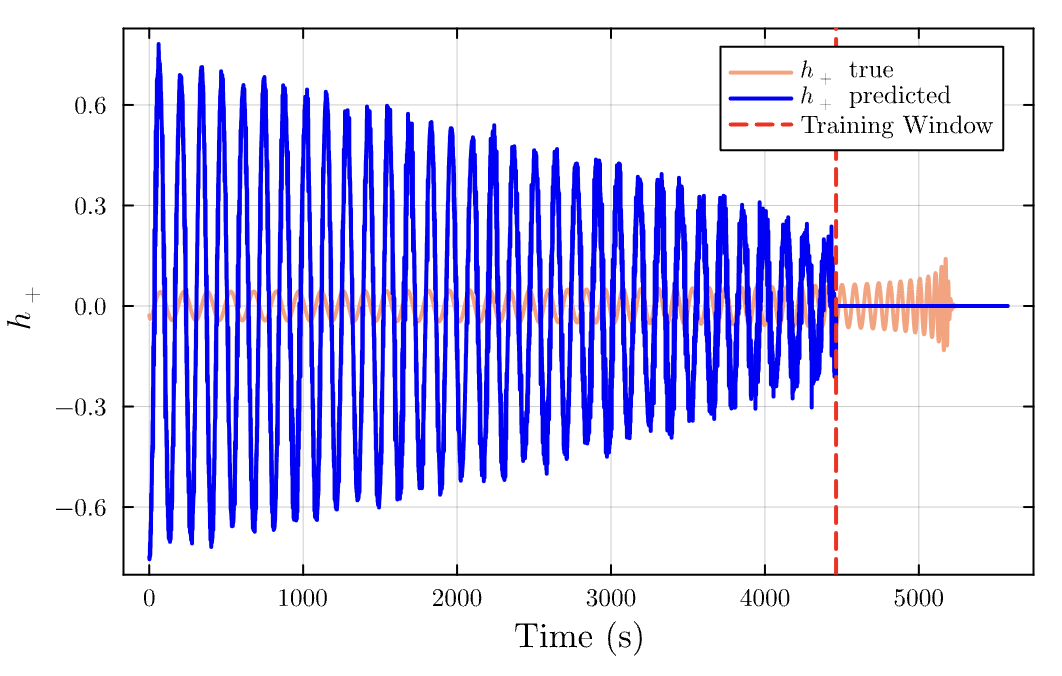
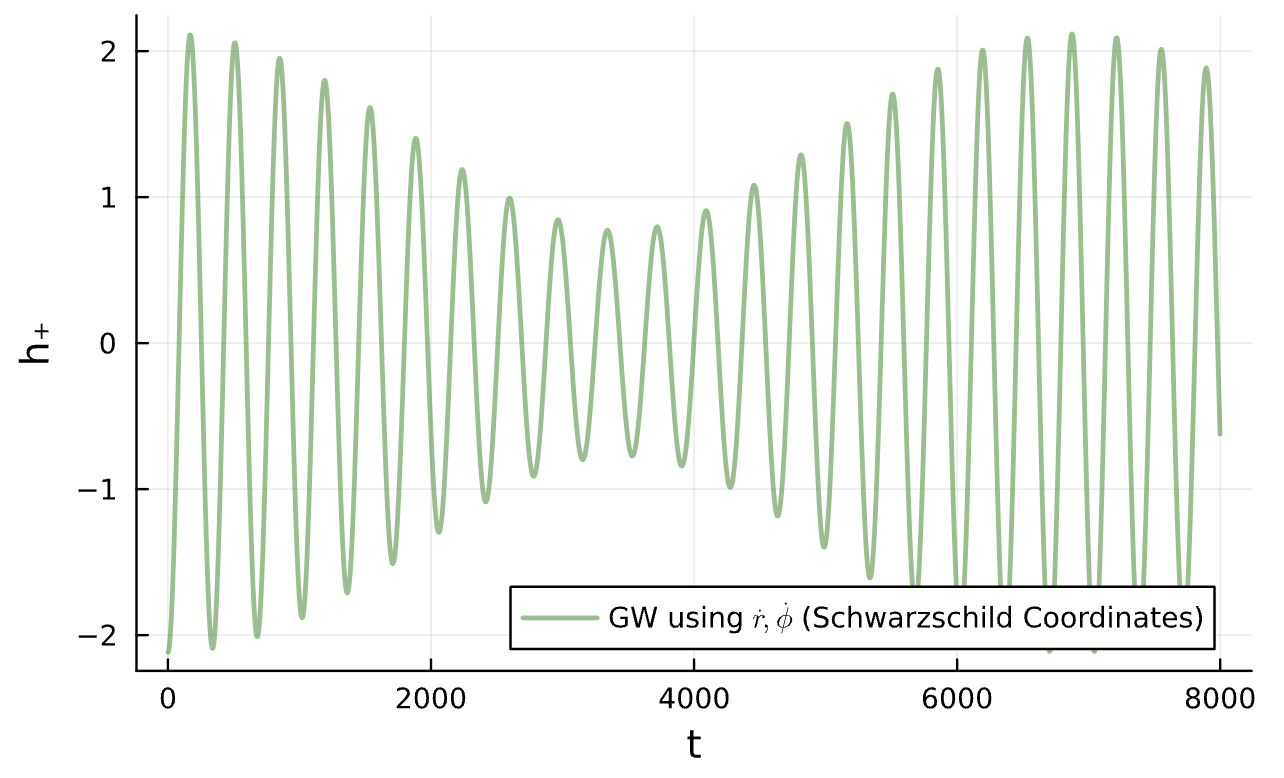
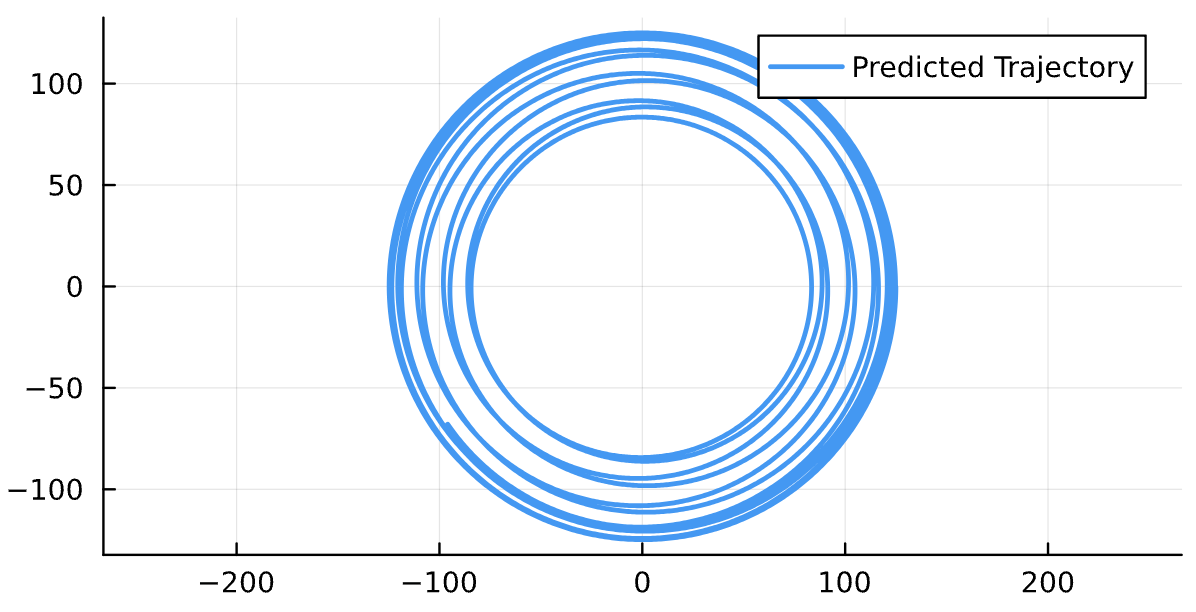
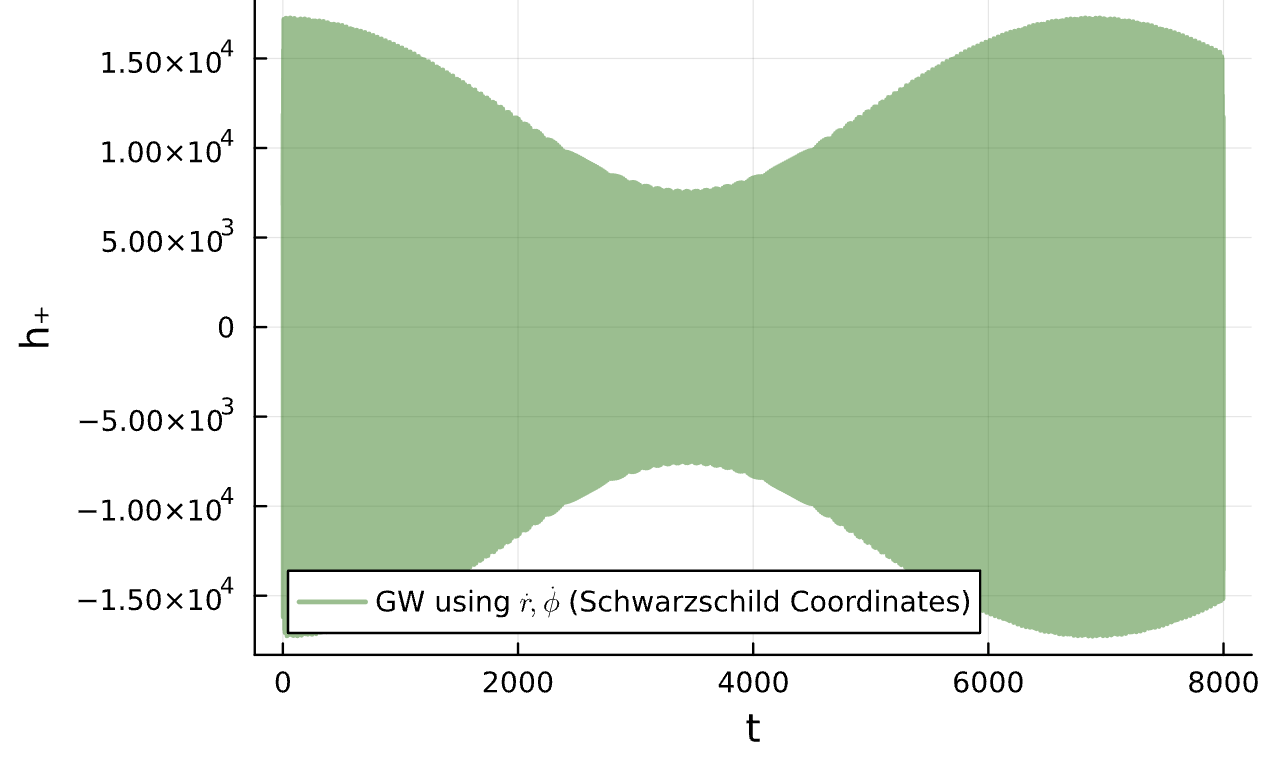
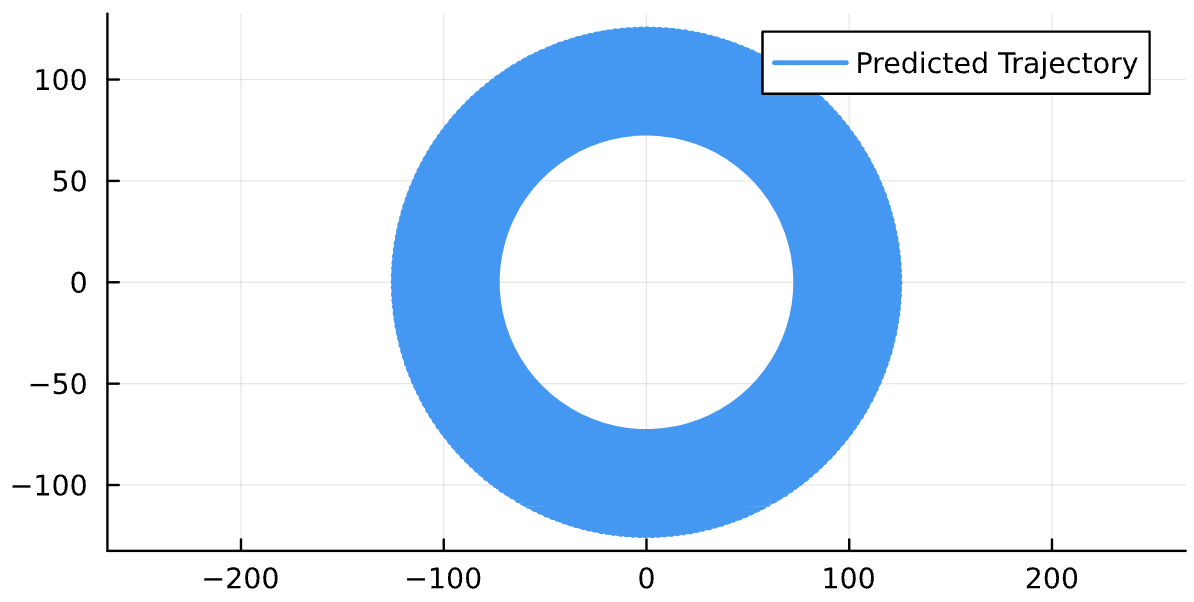
\dot \phi = \frac{\partial H}{\partial p_\phi}-TM_{25}, M_{25}>0
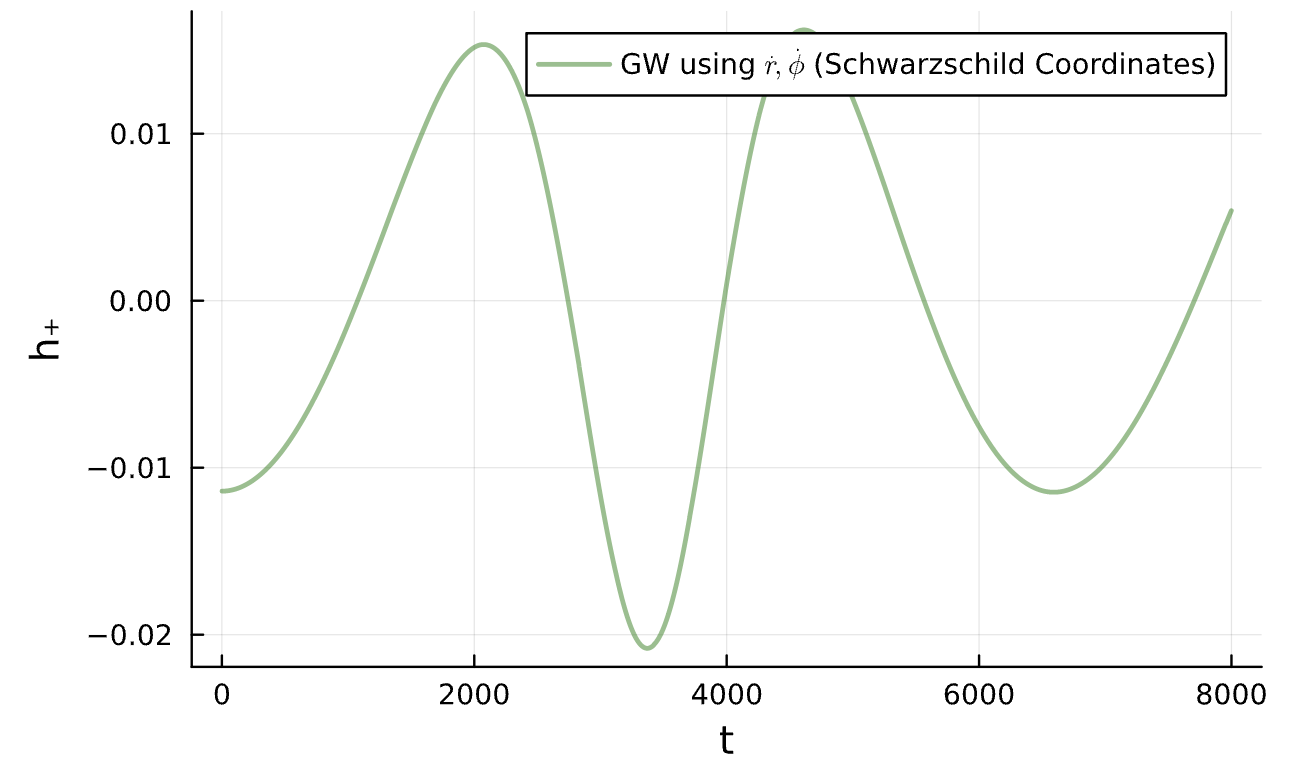
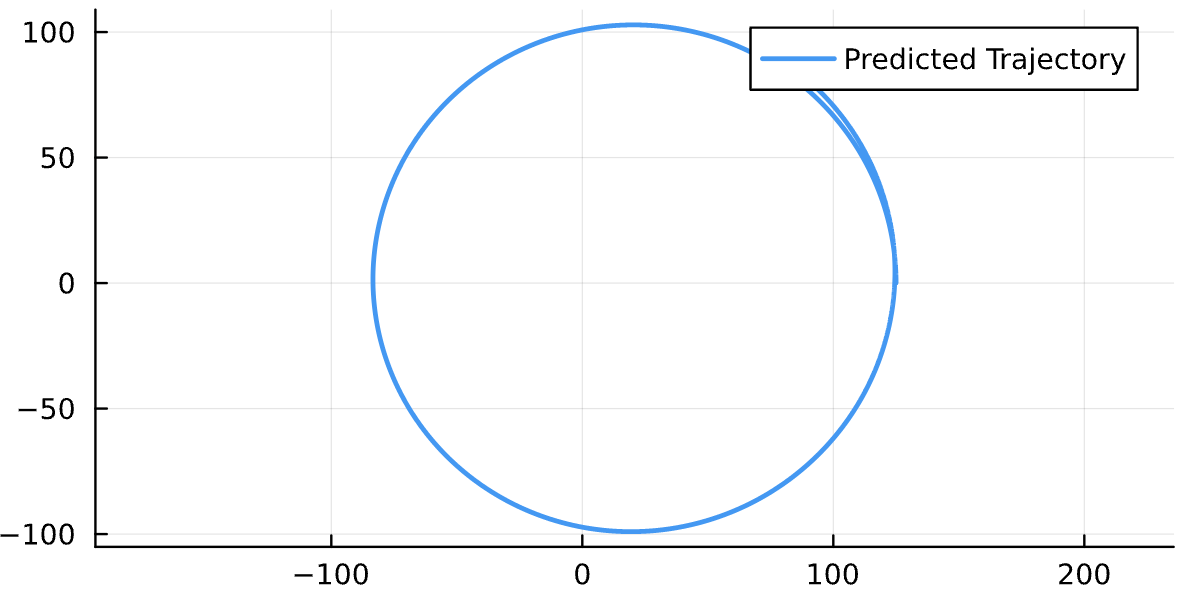
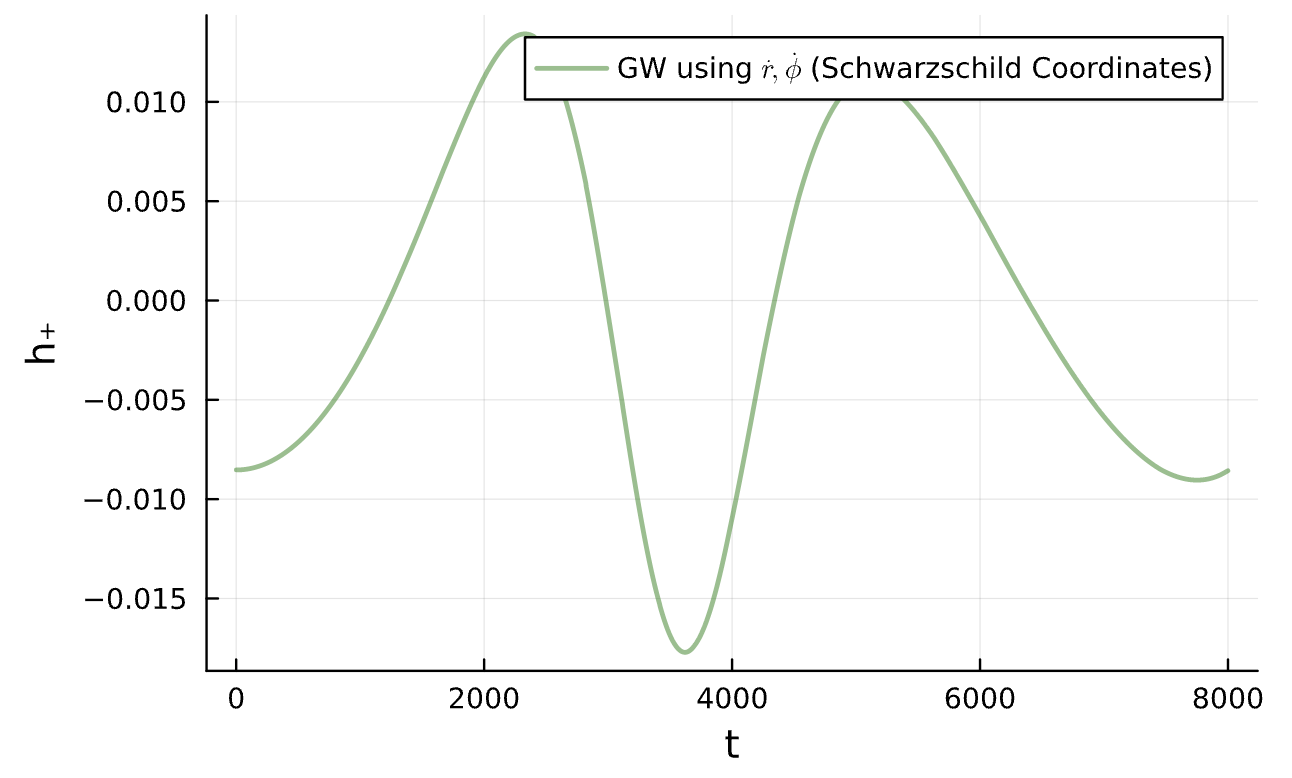
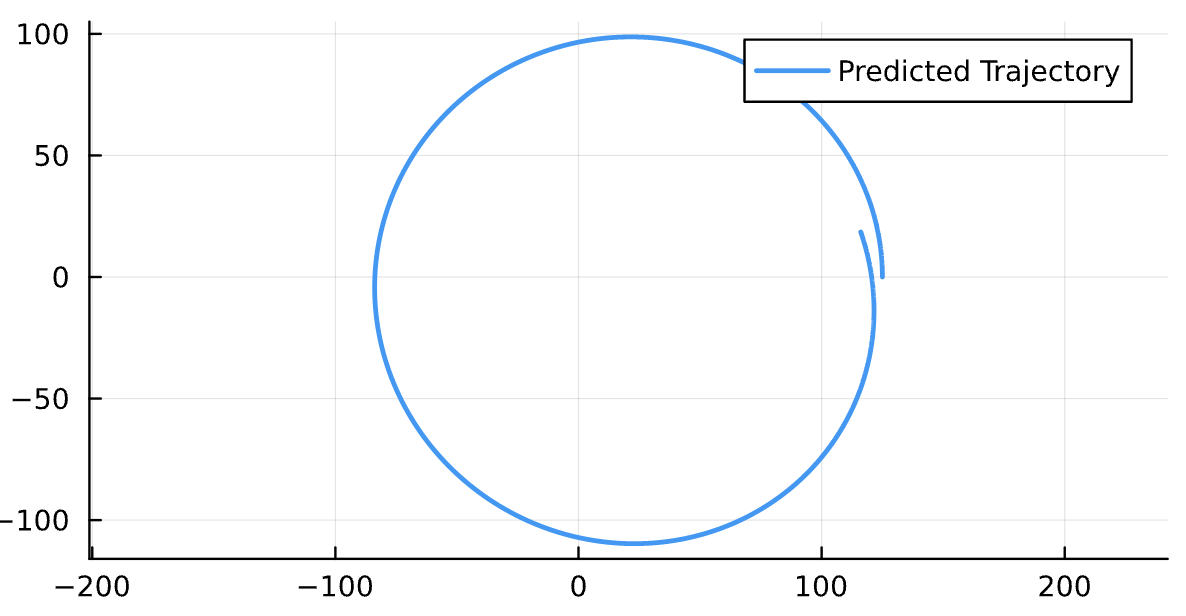
\dot \phi \text{ for different }(T,M_{25})
(1\mathrm{e}{-5},1\mathrm{e}{-5})
(1\mathrm{e}{-4},1\mathrm{e}{-4})
(1\mathrm{e}{-2},1\mathrm{e}{-2})
(1\mathrm{e}{-1},1\mathrm{e}{-1})
(1,1)
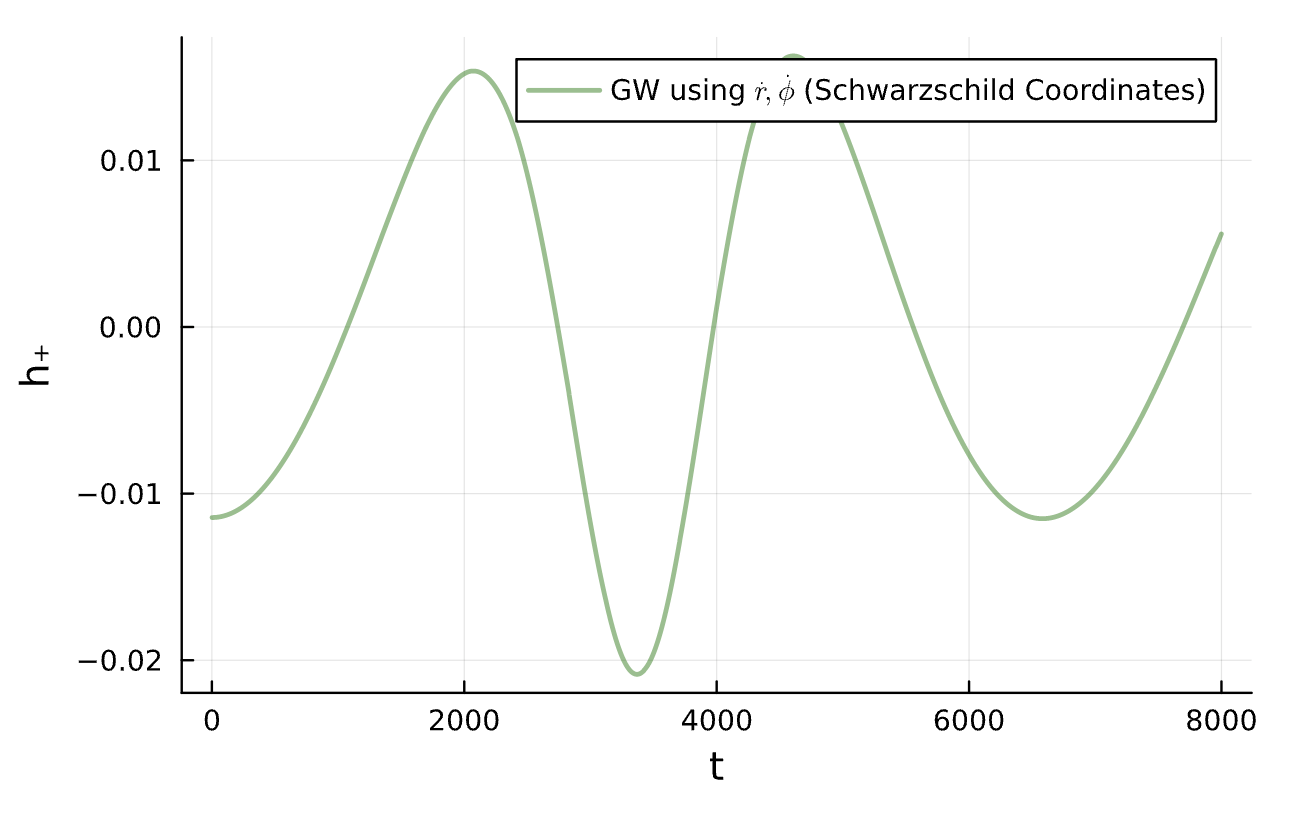
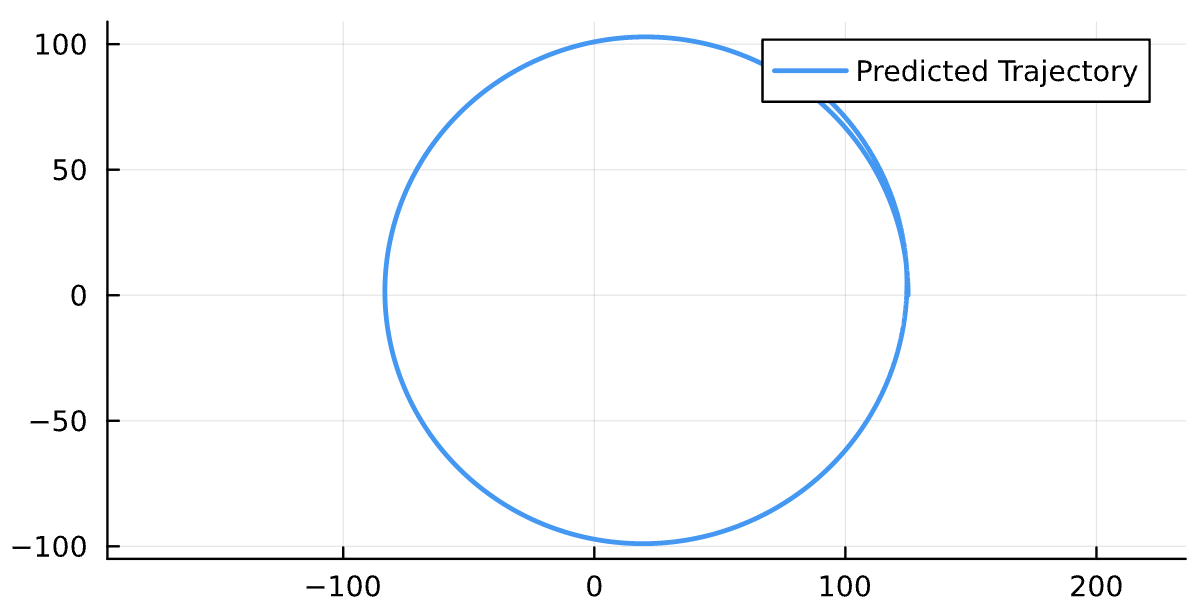
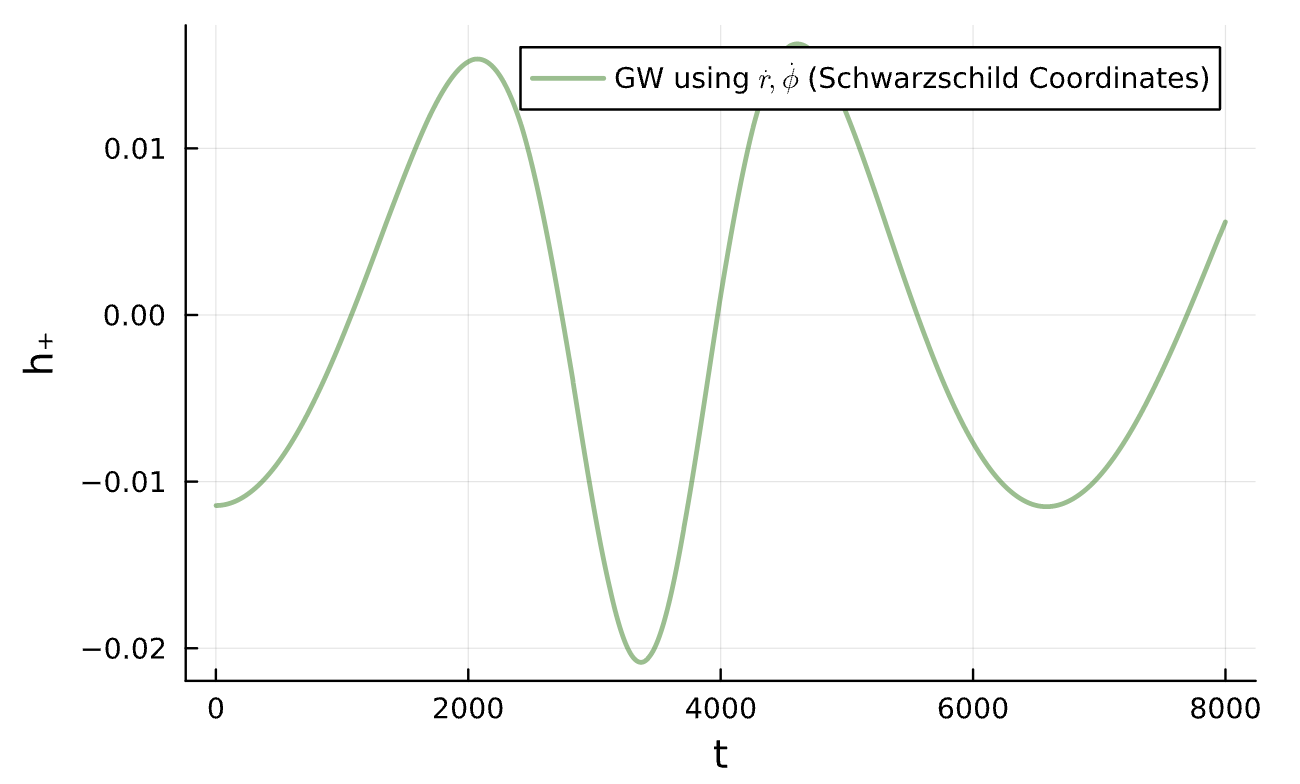
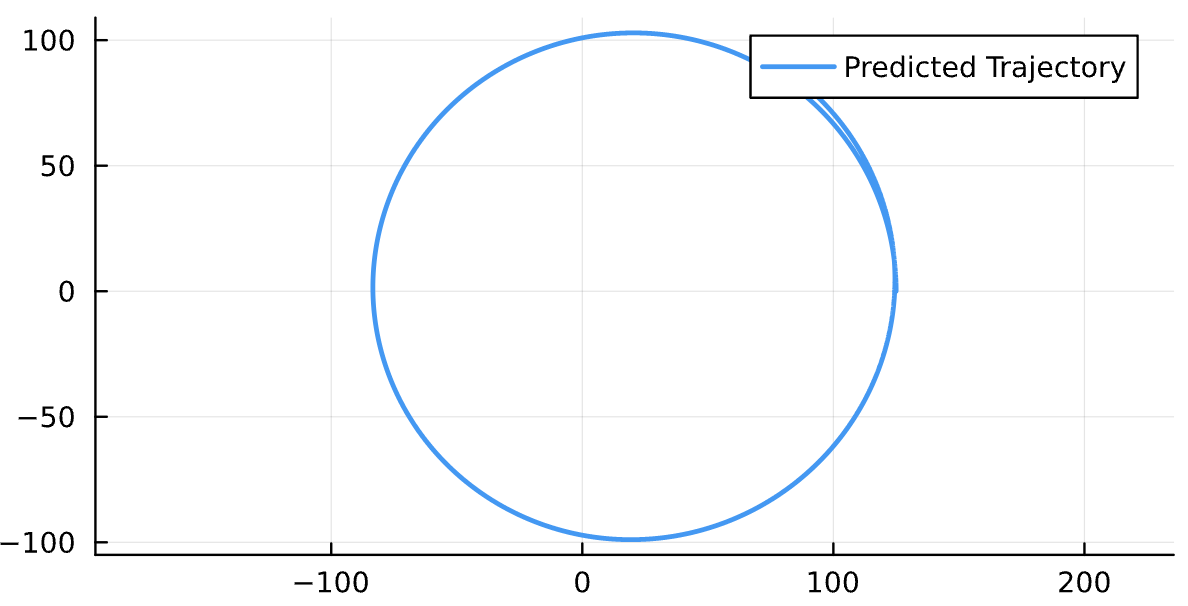
(1\mathrm{e}{-3},1\mathrm{e}{-3})
M_{11}\frac{\partial H}{\partial r}+M_{13}\frac{\partial H}{\partial p_r}+M_{14}\frac{\partial H}{\partial p_\phi}+M_{15}=0
M_{12}\frac{\partial H}{\partial r}+M_{23}\frac{\partial H}{\partial p_r}+M_{24}\frac{\partial H}{\partial p_\phi}+M_{25}=0
M_{13}\frac{\partial H}{\partial r}+M_{33}\frac{\partial H}{\partial p_r}+M_{34}\frac{\partial H}{\partial p_\phi}+M_{35}=0
M_{14}\frac{\partial H}{\partial r}+M_{34}\frac{\partial H}{\partial p_r}+M_{44}\frac{\partial H}{\partial p_\phi}+M_{45}=0
M_{15}\frac{\partial H}{\partial r}+M_{35}\frac{\partial H}{\partial p_r}+M_{45}\frac{\partial H}{\partial p_\phi}-M_{55}=0
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} -
\begin{pmatrix}
M_{15} \\
M_{25} \\
M_{35} \\
M_{45} \\
M_{55}
\end{pmatrix}
M_{11}\frac{\partial H}{\partial r}+M_{13}\frac{\partial H}{\partial p_r}+M_{14}\frac{\partial H}{\partial p_\phi}+M_{15}=0
M_{12}\frac{\partial H}{\partial r}+M_{23}\frac{\partial H}{\partial p_r}+M_{24}\frac{\partial H}{\partial p_\phi}+M_{25}=0
M_{13}\frac{\partial H}{\partial r}+M_{33}\frac{\partial H}{\partial p_r}+M_{34}\frac{\partial H}{\partial p_\phi}+M_{35}=0
M_{14}\frac{\partial H}{\partial r}+M_{34}\frac{\partial H}{\partial p_r}+M_{44}\frac{\partial H}{\partial p_\phi}+M_{45}=0
M_{15}\frac{\partial H}{\partial r}+M_{35}\frac{\partial H}{\partial p_r}+M_{45}\frac{\partial H}{\partial p_\phi}+M_{55}=0
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
M_{15} \\
0 \\
0 \\
0 \\
0
\end{pmatrix}
M_{15}>0
M_{11}=M_{13}=0
M_{14}\frac{\partial H}{\partial p_\phi}+M_{15}=0\to \boxed{M_{14}=-\left(\frac{\partial H}{\partial p_\phi} \right)^{-1}M_{15}}
\boxed{M_{15}>0}
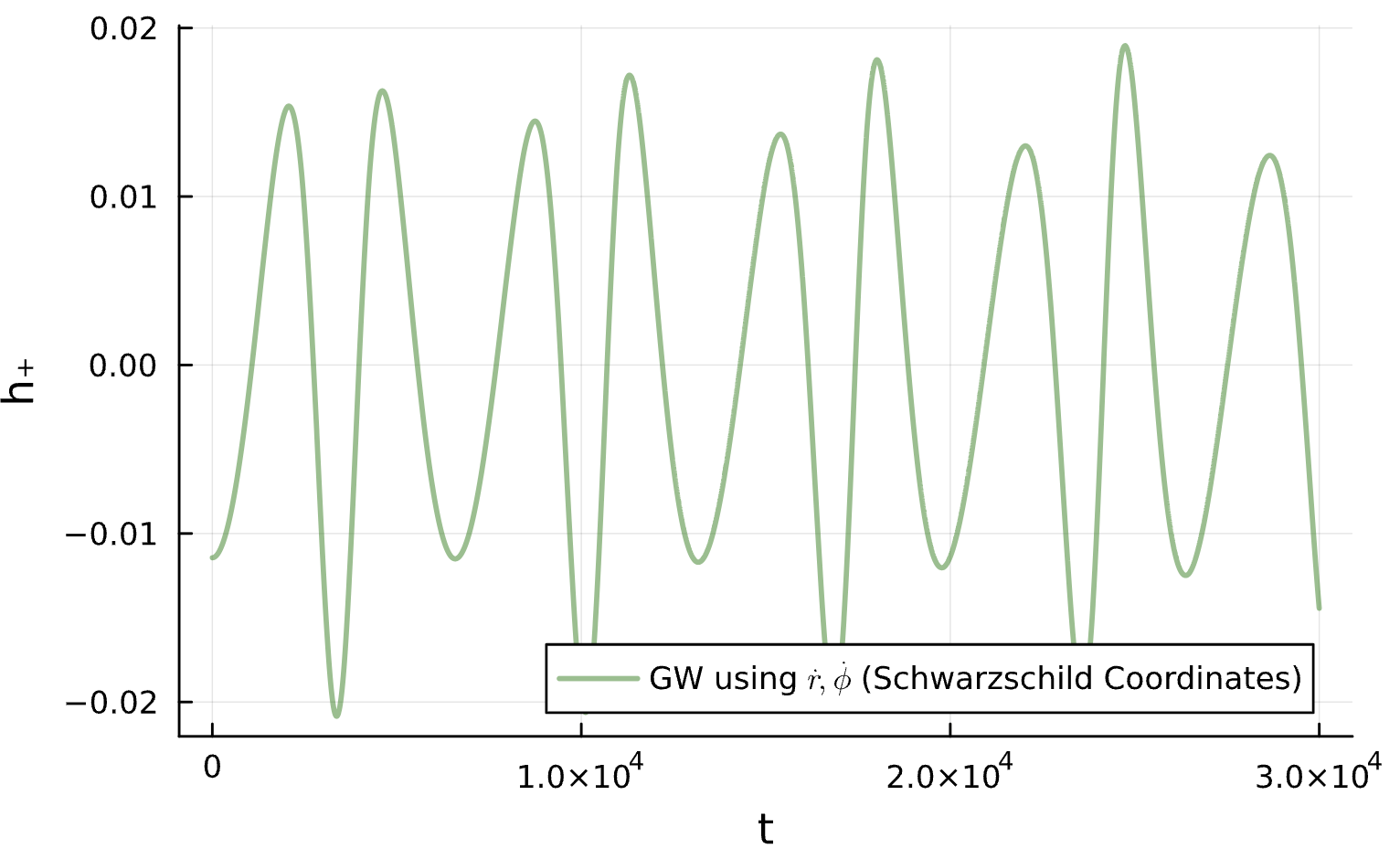
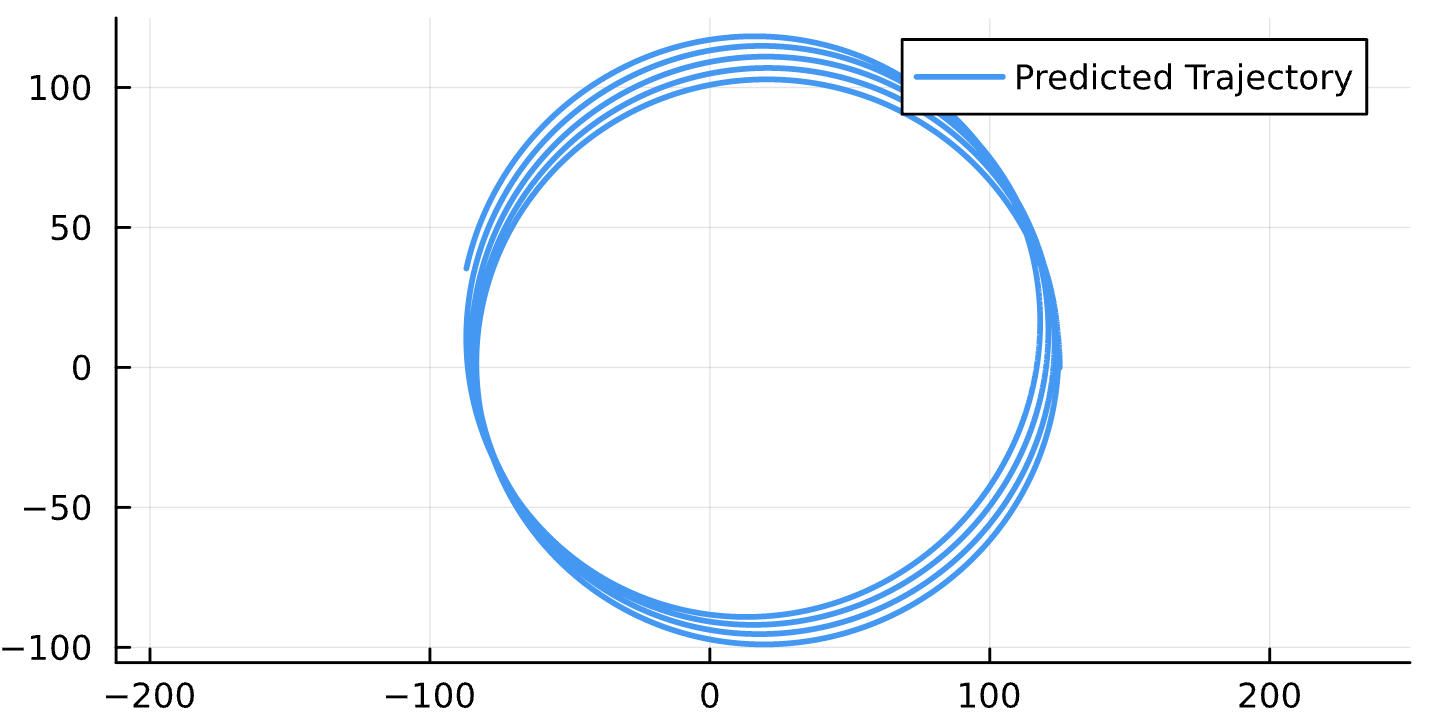
M_{15}=0
M_{15}=5\mathrm{e}{-2}
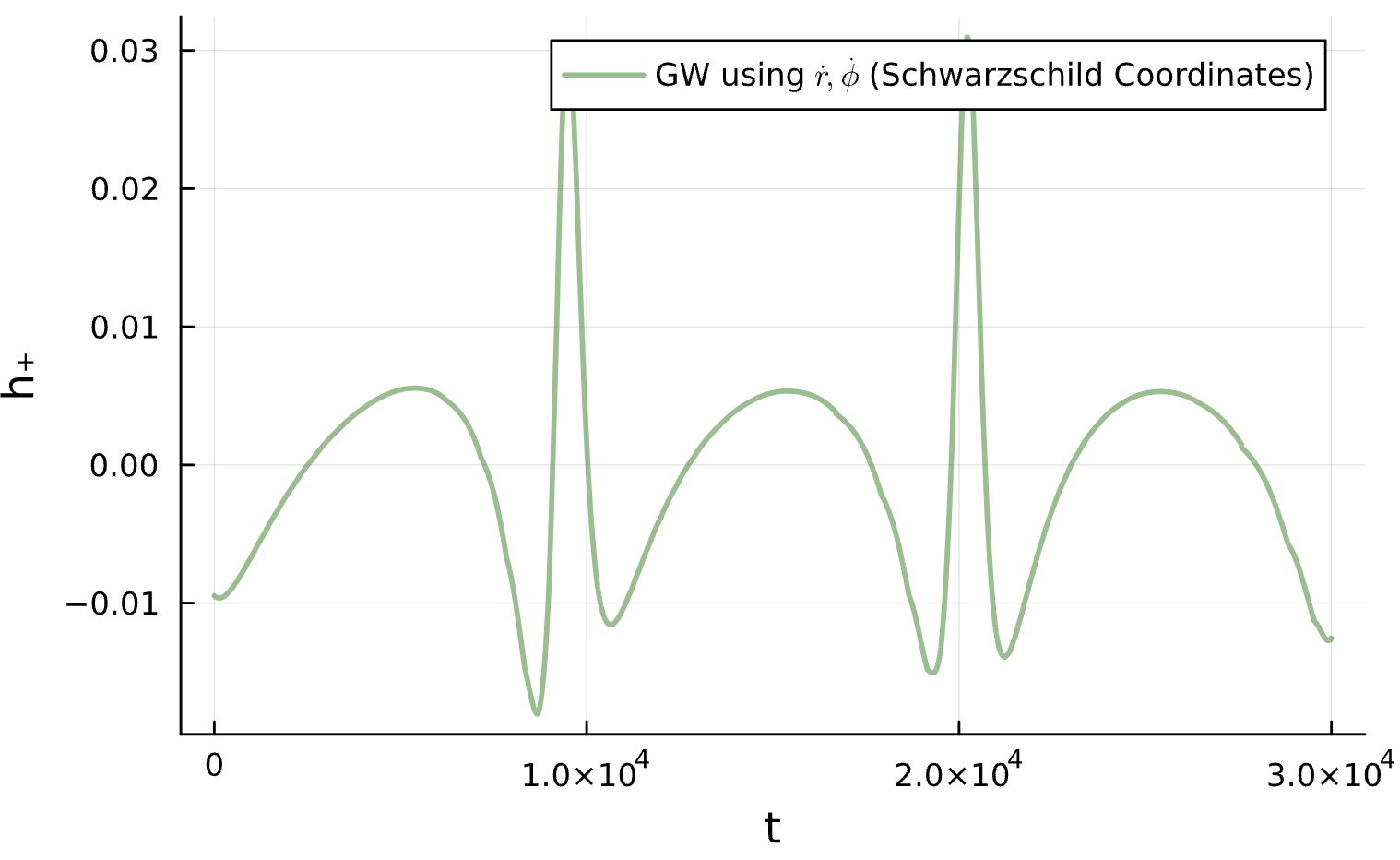
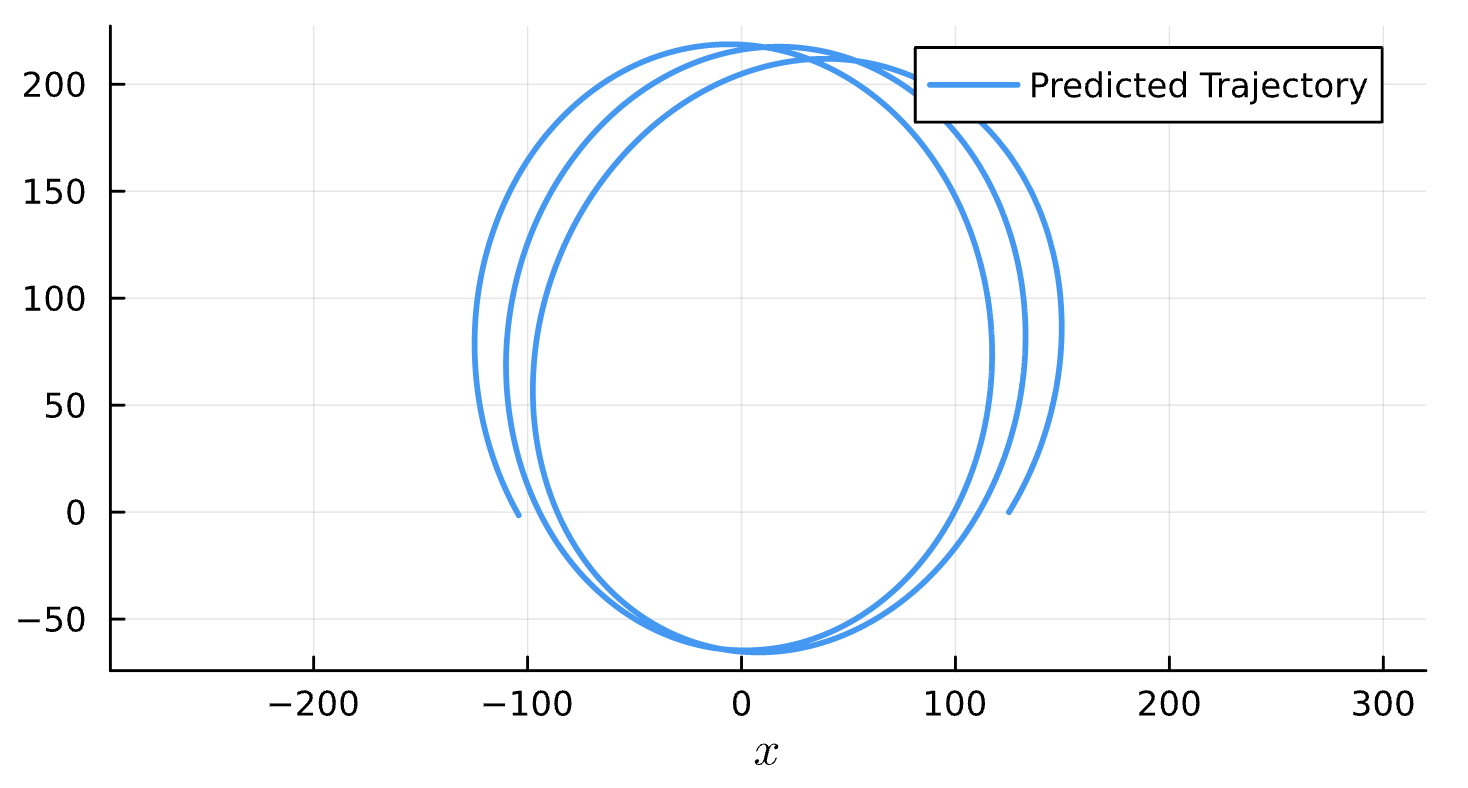
M_{12}\frac{\partial H}{\partial r}+M_{23}\frac{\partial H}{\partial p_r}+M_{24}\frac{\partial H}{\partial p_\phi}+M_{25}=0
M_{13}\frac{\partial H}{\partial r}+M_{33}\frac{\partial H}{\partial p_r}+M_{34}\frac{\partial H}{\partial p_\phi}+M_{35}=0
M_{14}\frac{\partial H}{\partial r}+M_{34}\frac{\partial H}{\partial p_r}+M_{44}\frac{\partial H}{\partial p_\phi}+M_{45}=0
M_{15}\frac{\partial H}{\partial r}+M_{35}\frac{\partial H}{\partial p_r}+M_{45}\frac{\partial H}{\partial p_\phi}+M_{55}=0
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
0 \\
M_{25} \\
0 \\
0 \\
0
\end{pmatrix}
M_{25}>0


M_{25}=0
M_{25}=5\mathrm{e}{-4}
M_{12}\frac{\partial H}{\partial r}+M_{23}\frac{\partial H}{\partial p_r}+M_{24}\frac{\partial H}{\partial p_\phi}+M_{25}=0
M_{12}=M_{23}=0
M_{24}\frac{\partial H}{\partial p_\phi}+M_{25}=0\to \boxed{M_{24}=-\left(\frac{\partial H}{\partial p_\phi} \right)^{-1}M_{25}}
\boxed{M_{25}>0}
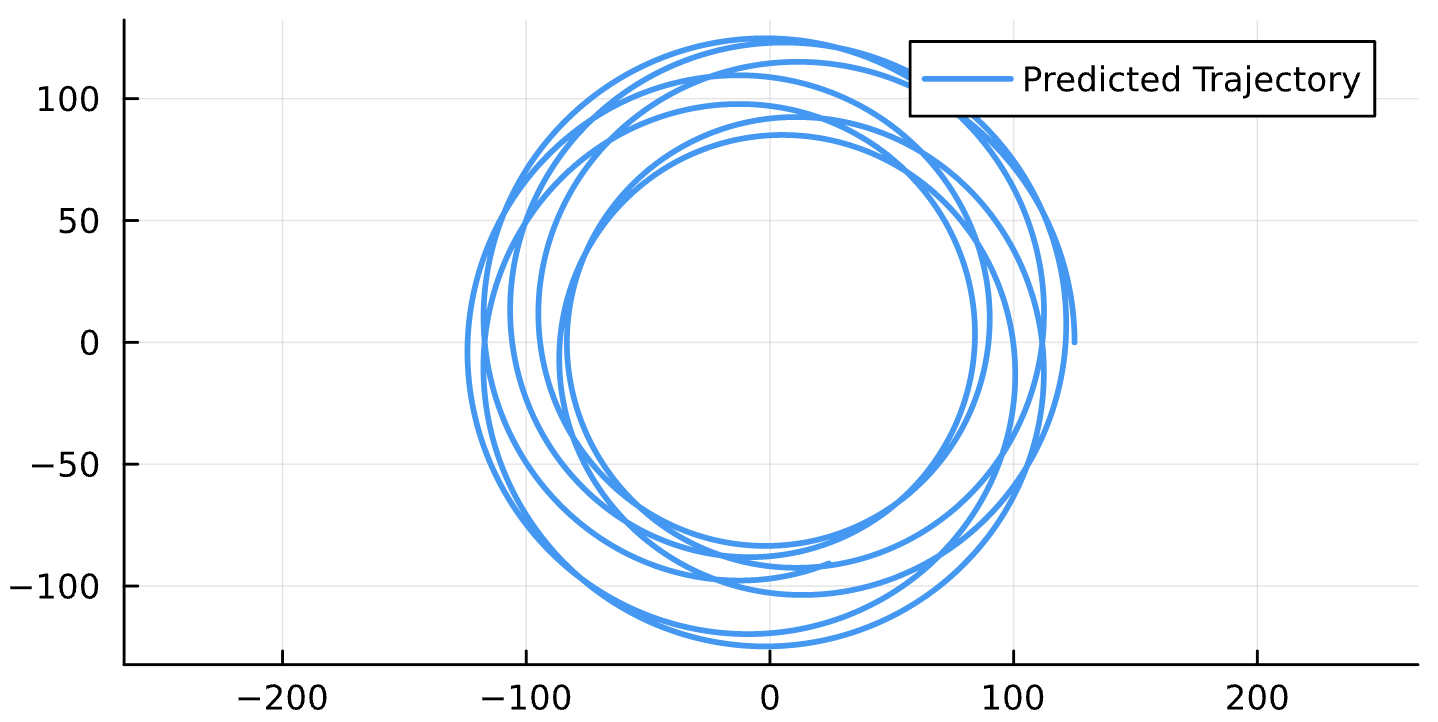
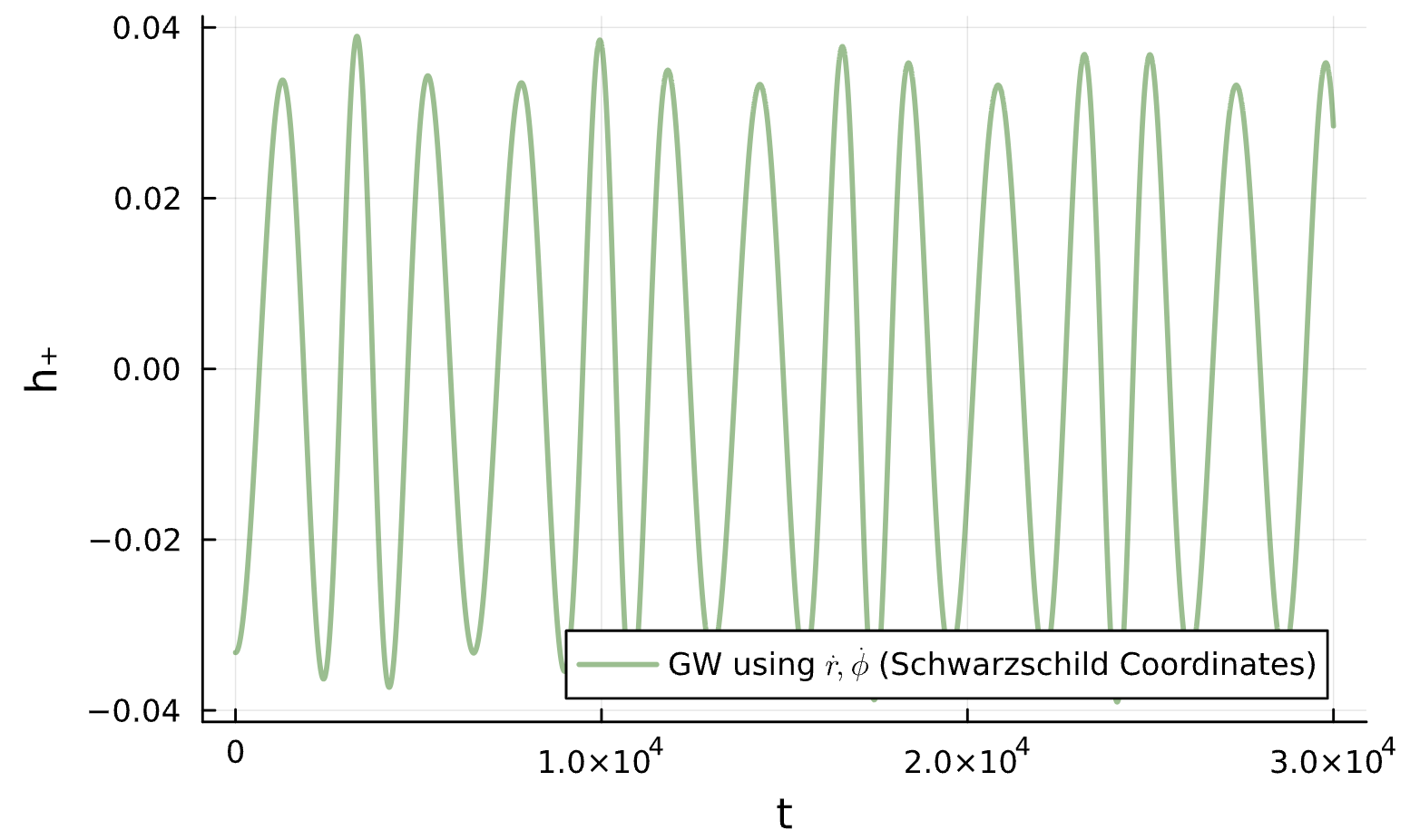
M_{12}\frac{\partial H}{\partial r}+M_{23}\frac{\partial H}{\partial p_r}+M_{24}\frac{\partial H}{\partial p_\phi}+M_{25}=0
M_{13}\frac{\partial H}{\partial r}+M_{33}\frac{\partial H}{\partial p_r}+M_{34}\frac{\partial H}{\partial p_\phi}+M_{35}=0
M_{14}\frac{\partial H}{\partial r}+M_{34}\frac{\partial H}{\partial p_r}+M_{44}\frac{\partial H}{\partial p_\phi}+M_{45}=0
M_{15}\frac{\partial H}{\partial r}+M_{35}\frac{\partial H}{\partial p_r}+M_{45}\frac{\partial H}{\partial p_\phi}+M_{55}=0
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
0 \\
0\\
M_{35} \\
0 \\
0
\end{pmatrix}
M_{35}>0


M_{35}=0
M_{35}=1.44\mathrm{e}{-5}
M_{13}=M_{33}=0
M_{34}\frac{\partial H}{\partial p_\phi}+M_{35}=0\to \boxed{M_{34}=-\left(\frac{\partial H}{\partial p_\phi} \right)^{-1}M_{35}}
\boxed{M_{35}>0}
M_{13}\frac{\partial H}{\partial r}+M_{33}\frac{\partial H}{\partial p_r}+M_{34}\frac{\partial H}{\partial p_\phi}+M_{35}=0
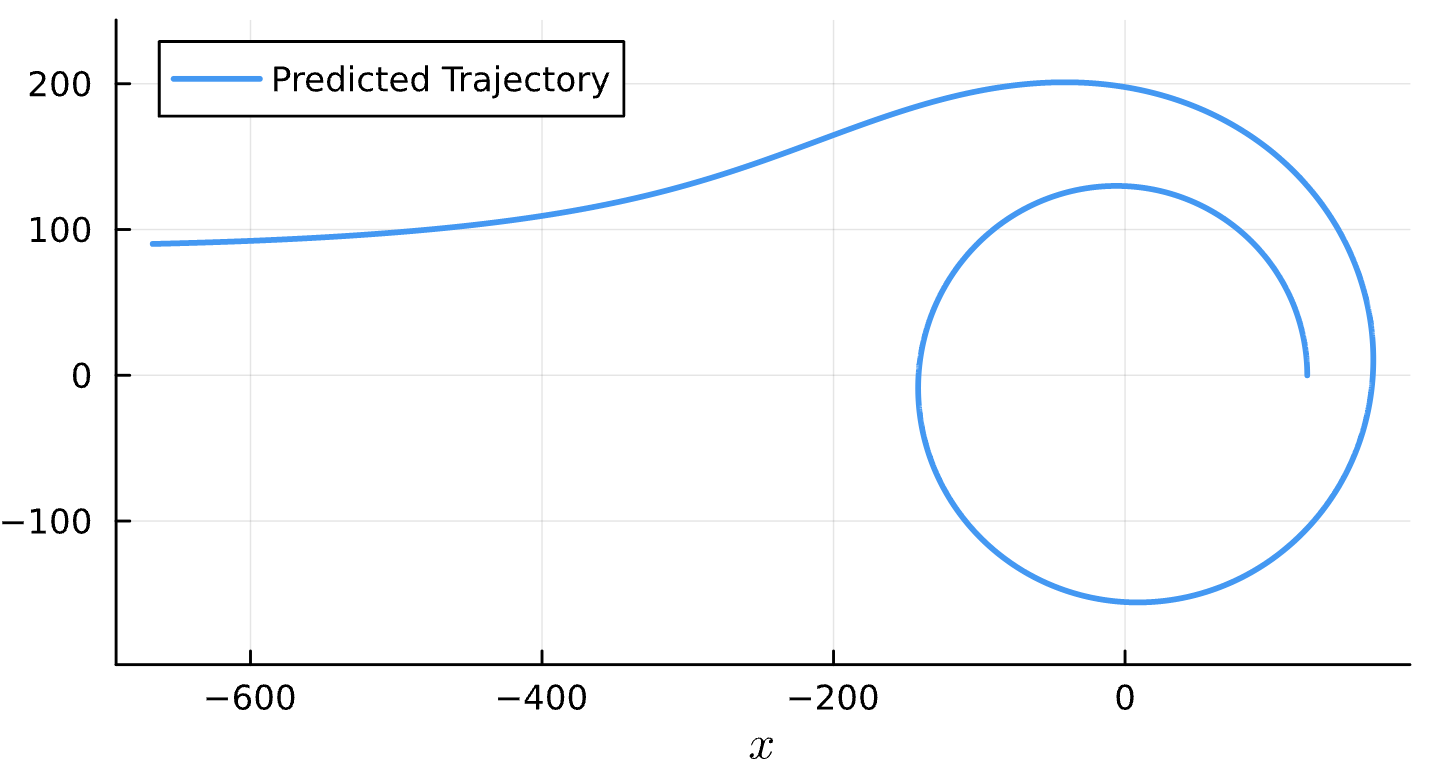
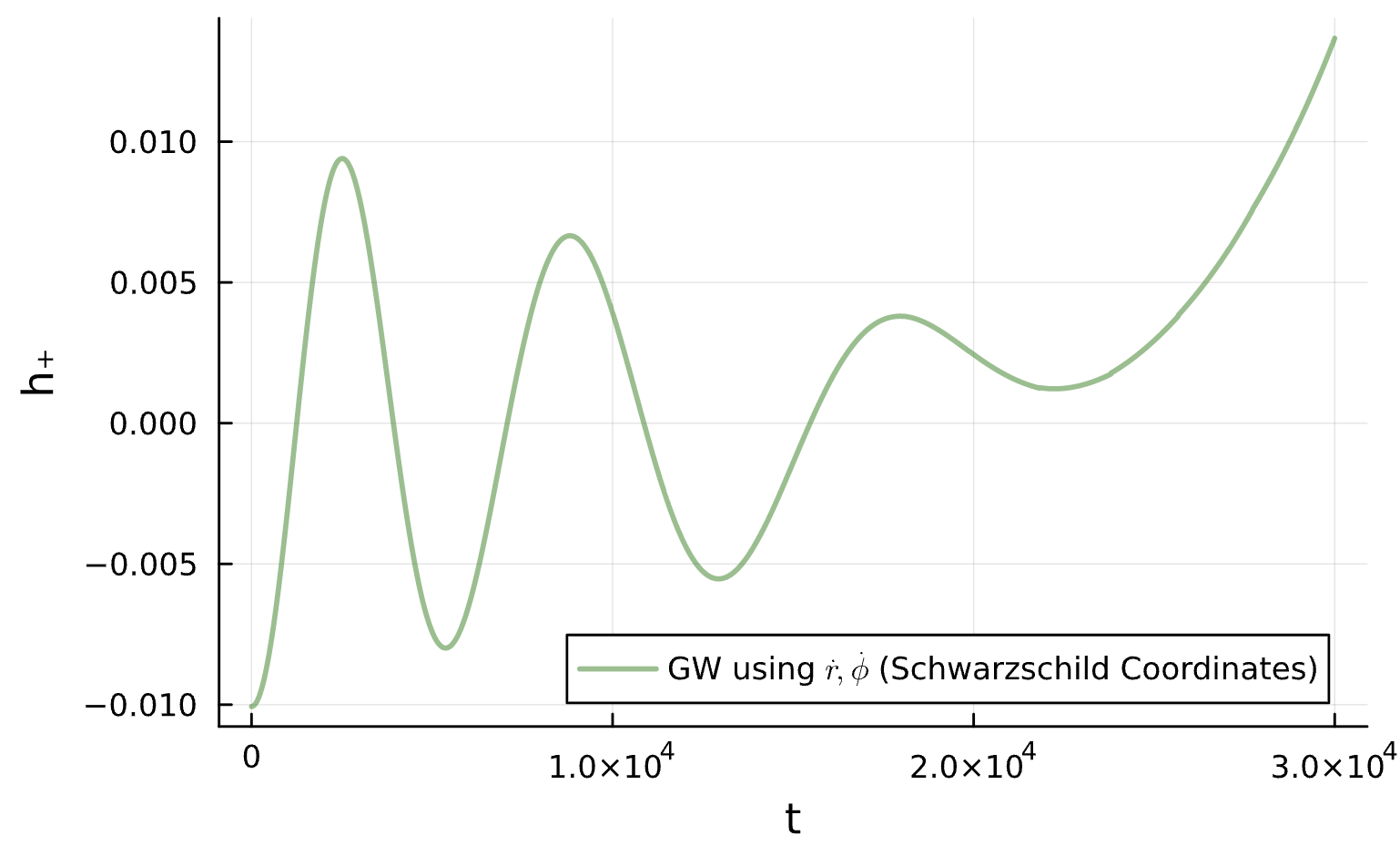
M_{12}\frac{\partial H}{\partial r}+M_{23}\frac{\partial H}{\partial p_r}+M_{24}\frac{\partial H}{\partial p_\phi}+M_{25}=0
M_{13}\frac{\partial H}{\partial r}+M_{33}\frac{\partial H}{\partial p_r}+M_{34}\frac{\partial H}{\partial p_\phi}+M_{35}=0
M_{14}\frac{\partial H}{\partial r}+M_{34}\frac{\partial H}{\partial p_r}+M_{44}\frac{\partial H}{\partial p_\phi}+M_{45}=0
M_{15}\frac{\partial H}{\partial r}+M_{35}\frac{\partial H}{\partial p_r}+M_{45}\frac{\partial H}{\partial p_\phi}+M_{55}=0
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
0 \\
0\\
0 \\
M_{45} \\
0
\end{pmatrix}
M_{45}>0


M_{45}=0
M_{45}=2\mathrm{e}{-4}
M_{14}\frac{\partial H}{\partial r}+M_{34}\frac{\partial H}{\partial p_r}+M_{44}\frac{\partial H}{\partial p_\phi}+M_{45}=0
M_{14}=M_{34}=0
M_{44}\frac{\partial H}{\partial p_\phi}+M_{45}=0\to \boxed{M_{44}=-\left(\frac{\partial H}{\partial p_\phi} \right)^{-1}M_{45}}
\boxed{M_{45}>0}
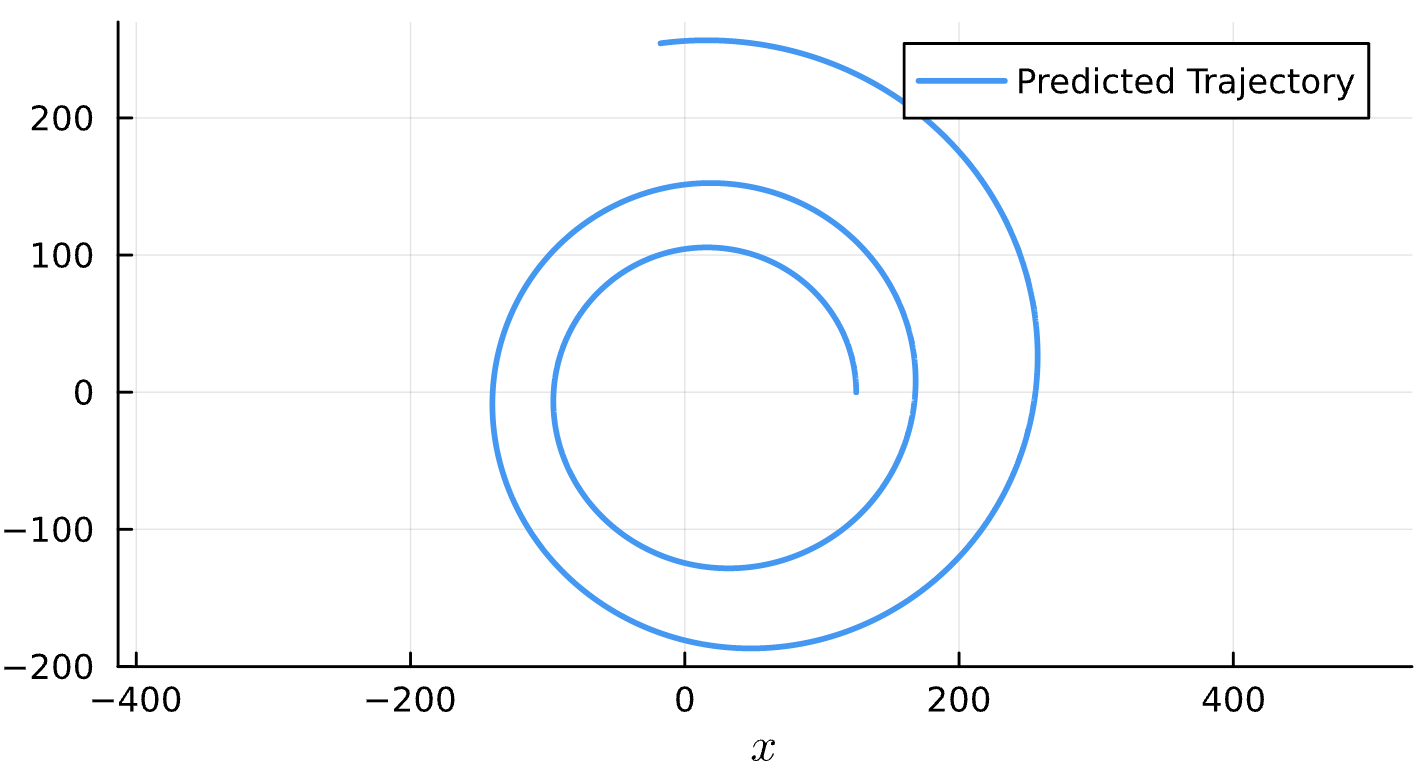
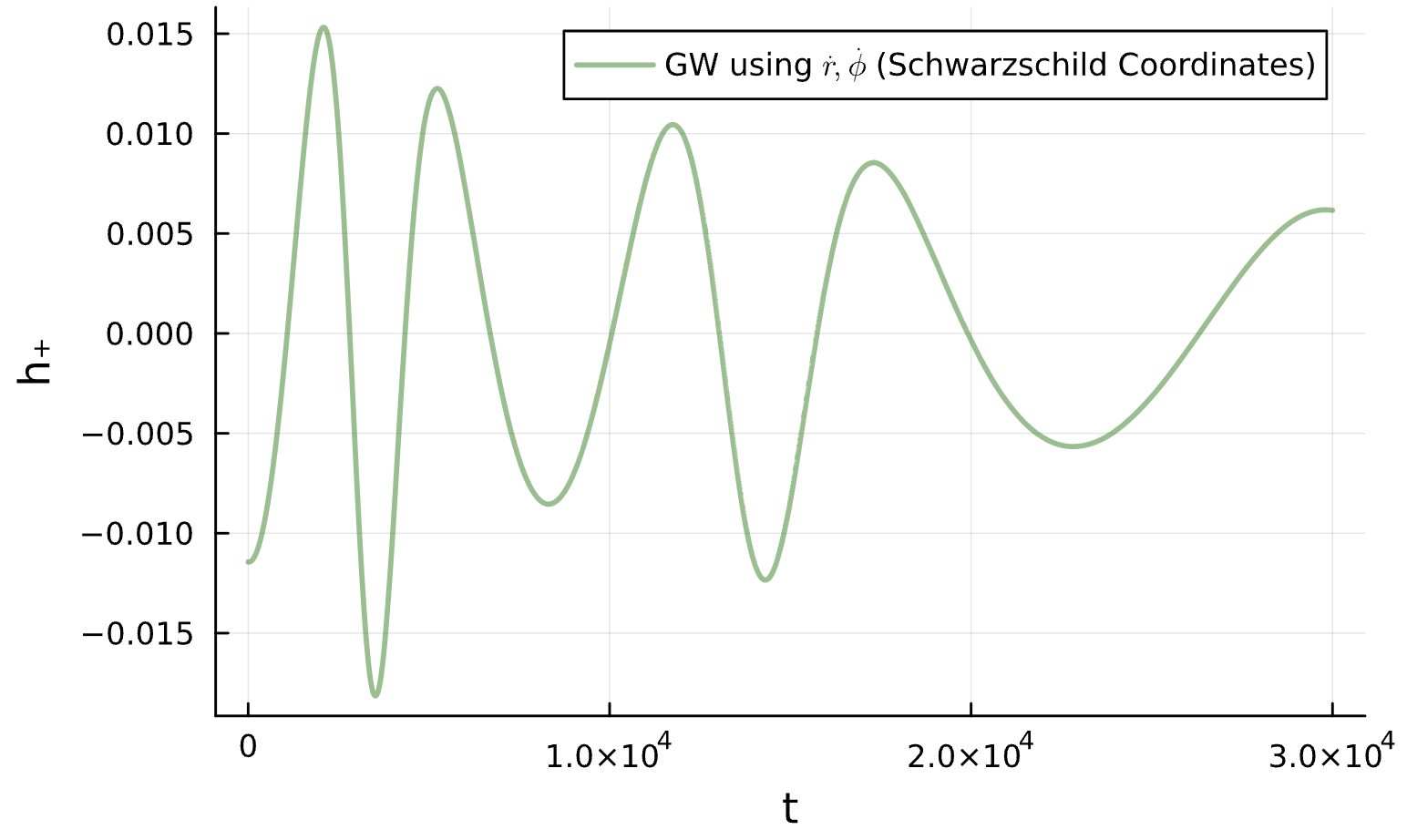
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
0 \\
0\\
M_{35} \\
0 \\
M_{55}
\end{pmatrix}
M_{55}>0
M_{15}=M_{45}=0
M_{35}=-\left(\frac{\partial H}{\partial p_r} \right)^{-1}M_{55}
M_{35}\frac{\partial H}{\partial p_r}+M_{55}=0 \to \boxed{M_{35} = -\left(\frac{\partial H}{\partial p_r} \right)^{-1} M_{55}}
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
M_{15} \\
0\\
0 \\
0 \\
M_{55}
\end{pmatrix}
M_{55}>0
M_{35}=M_{45}=0
M_{15}=-\left(\frac{\partial H}{\partial r} \right)^{-1}M_{55}
M_{15}\frac{\partial H}{\partial r}+M_{55}=0 \to \boxed{M_{15}=\left(\frac{\partial H}{\partial r} \right)^{-1} M_{55}}
\begin{pmatrix}
\dot r \\
\dot \phi \\
\dot p_r \\
\dot p_\phi \\
\dot S
\end{pmatrix}=
\begin{pmatrix}
\frac{\partial H}{\partial p_r} \\
\frac{\partial H}{\partial p_\phi} \\
-\frac{\partial H}{\partial r} \\
0 \\
0
\end{pmatrix} +
\begin{pmatrix}
0 \\
0\\
0 \\
- p_\phi \\
p_\phi
\end{pmatrix}
\dot p_\phi \propto -p_\phi
Binary Black Holes | 08/12 Update
By Ref Bari
Binary Black Holes | 08/12 Update
- 206


