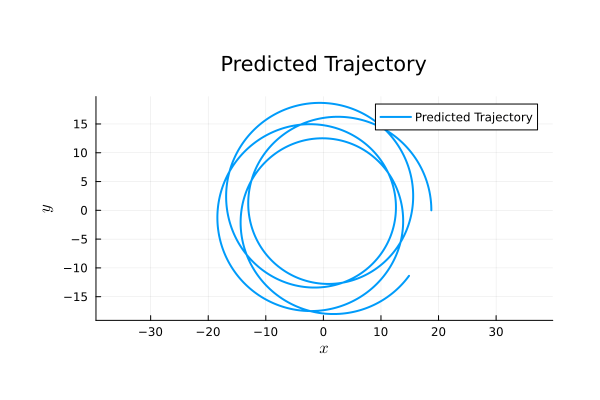
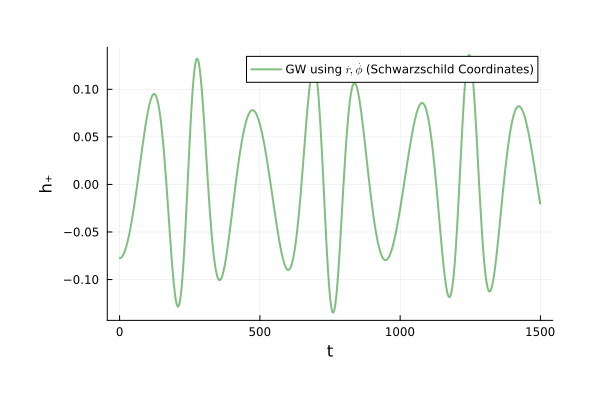
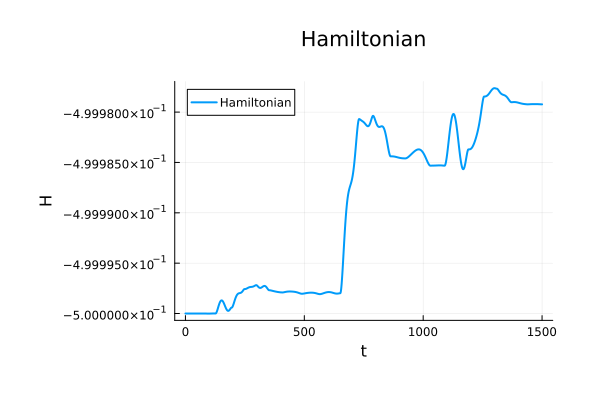
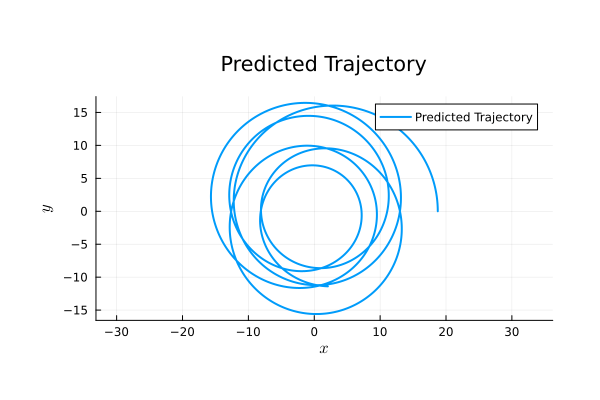
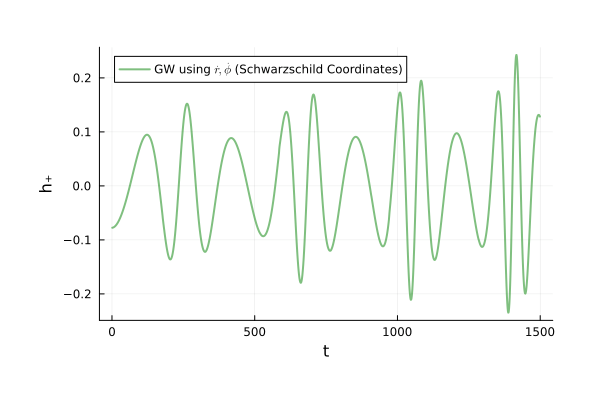
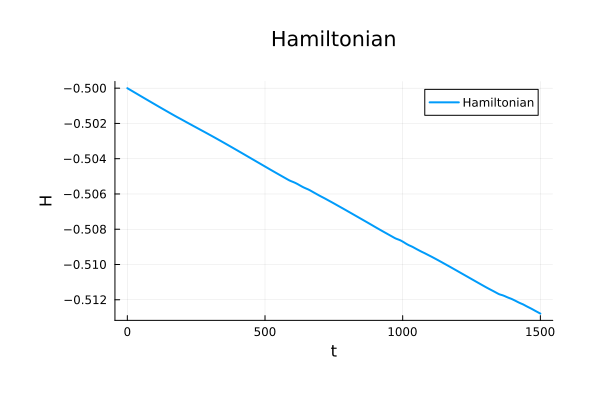
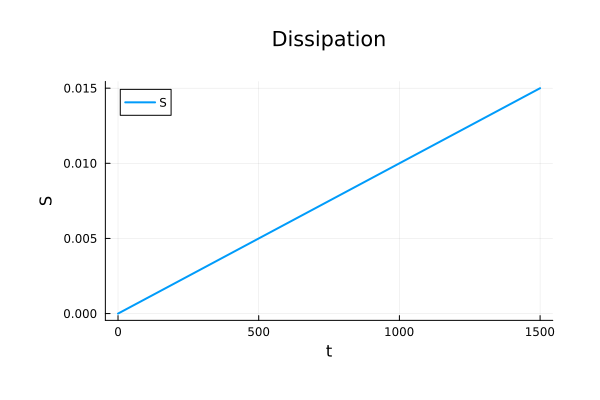
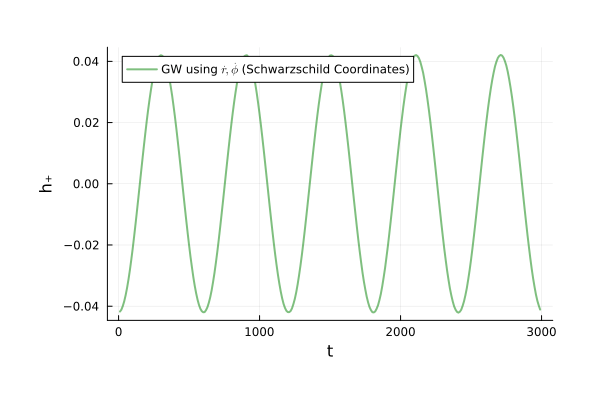
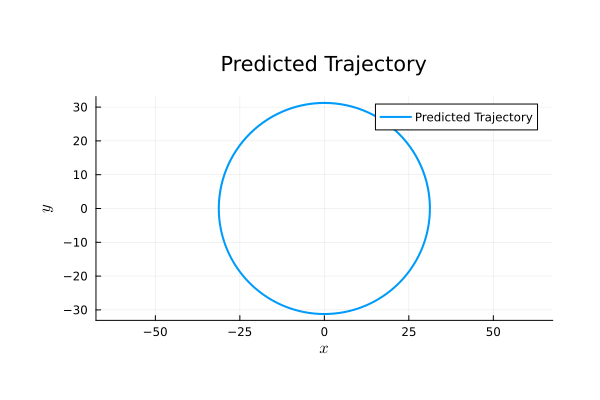
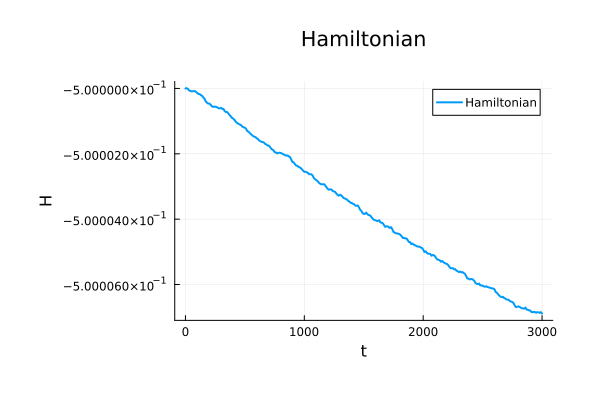
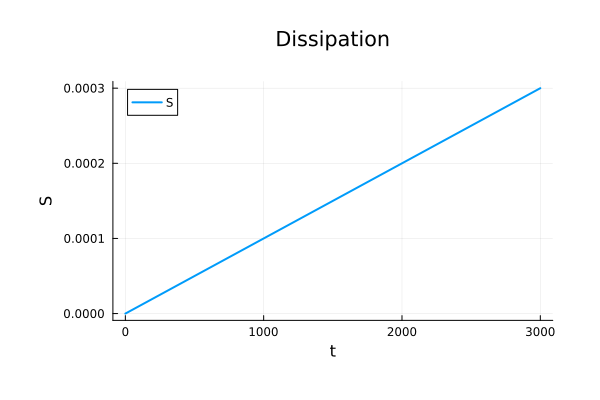
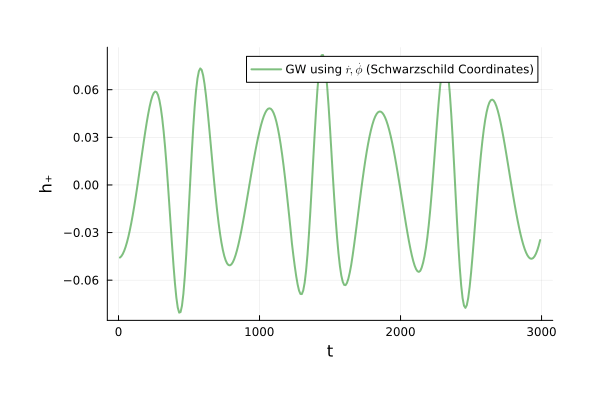
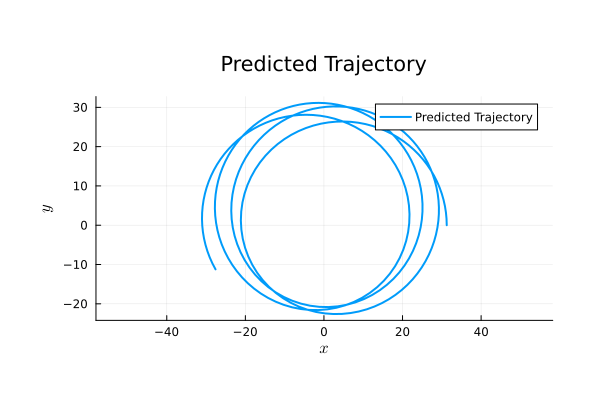
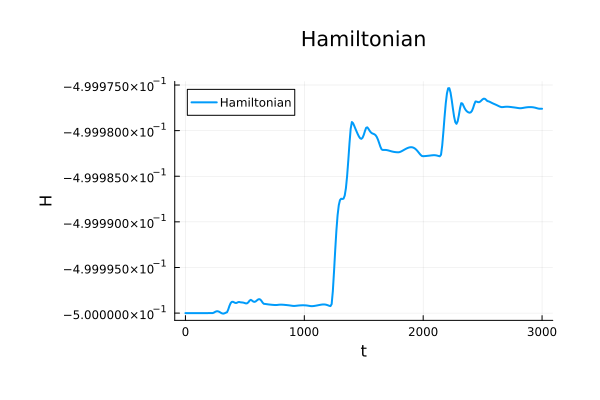
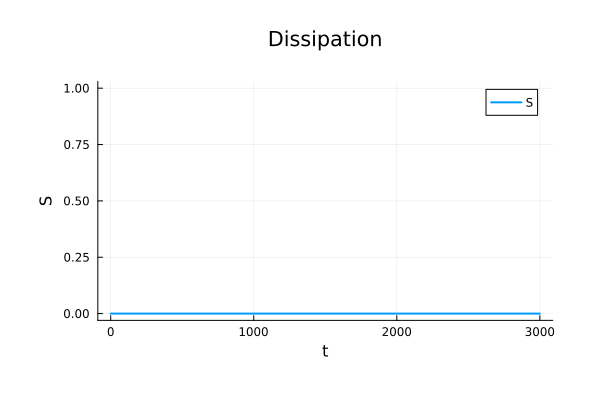
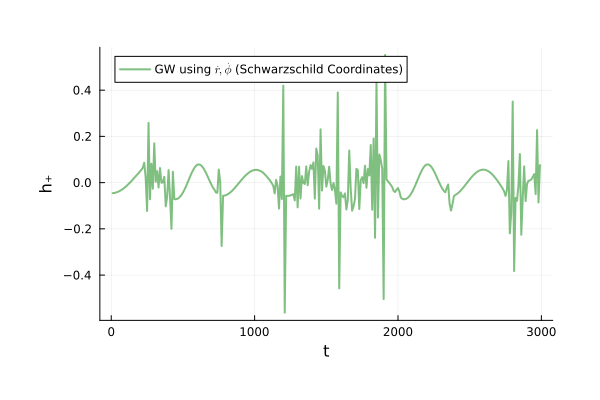
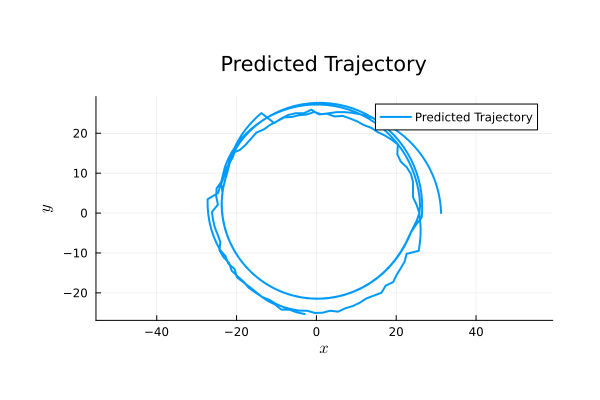
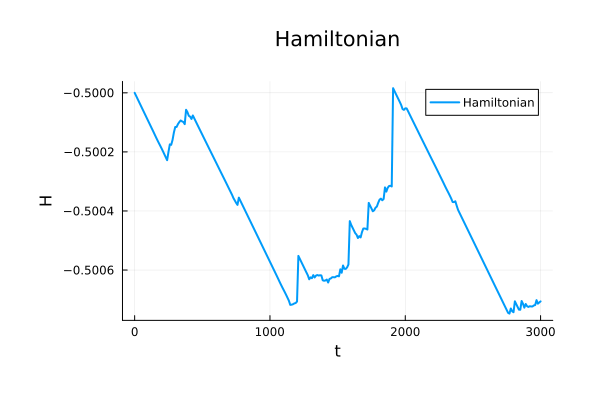
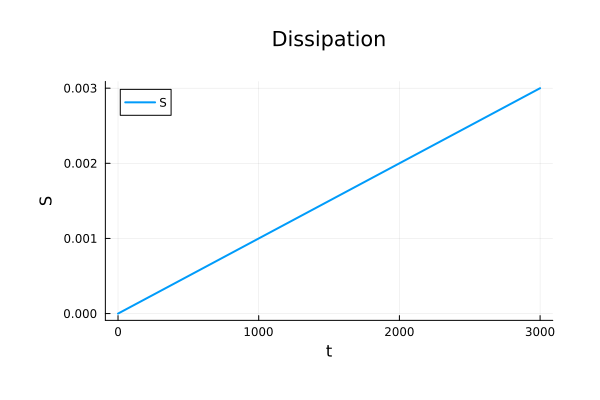
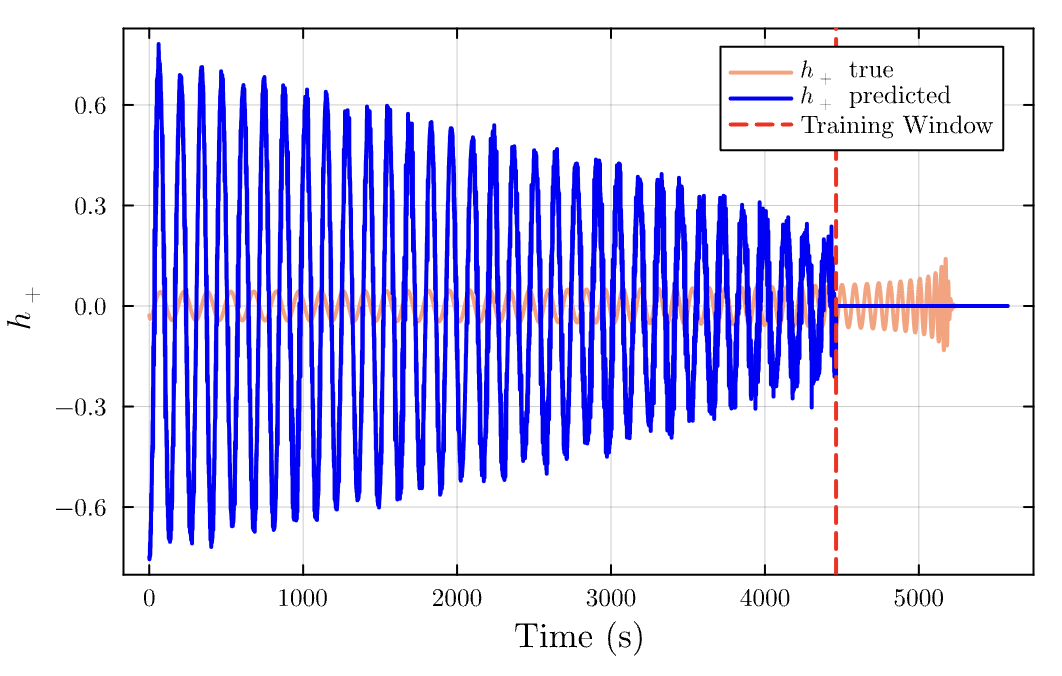
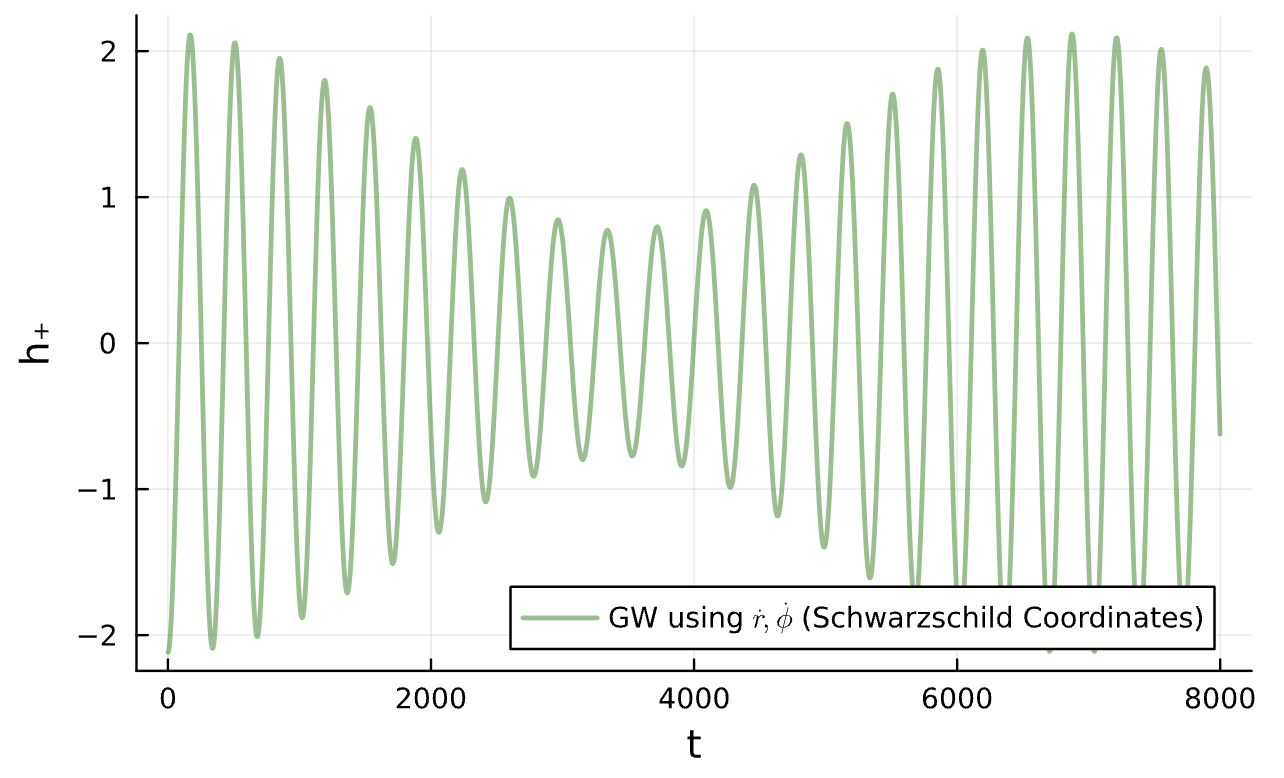
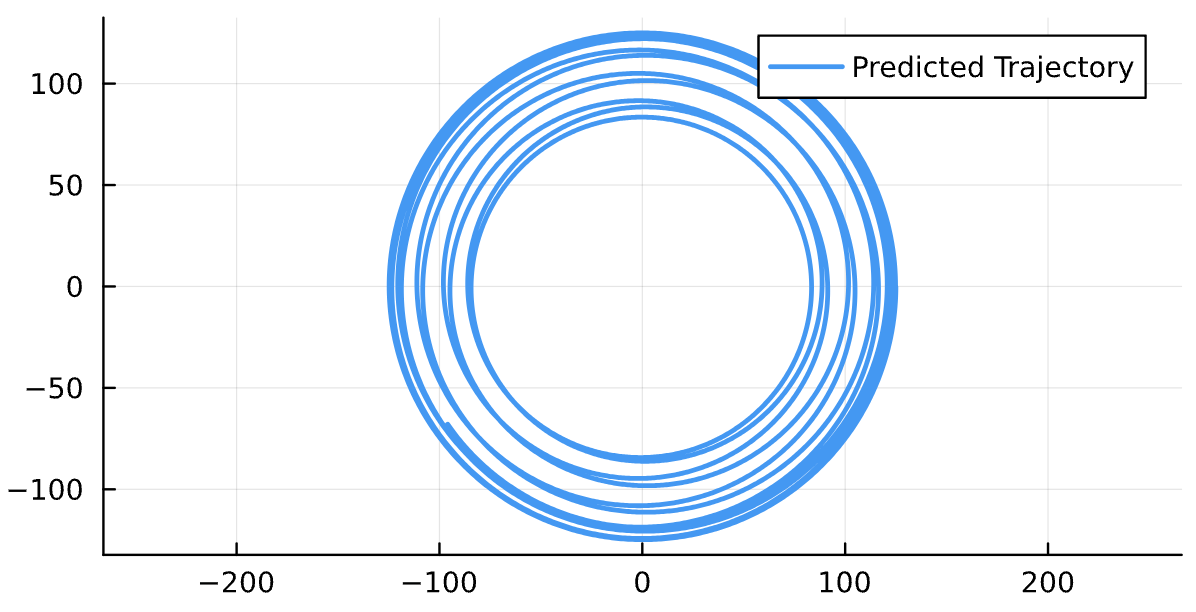
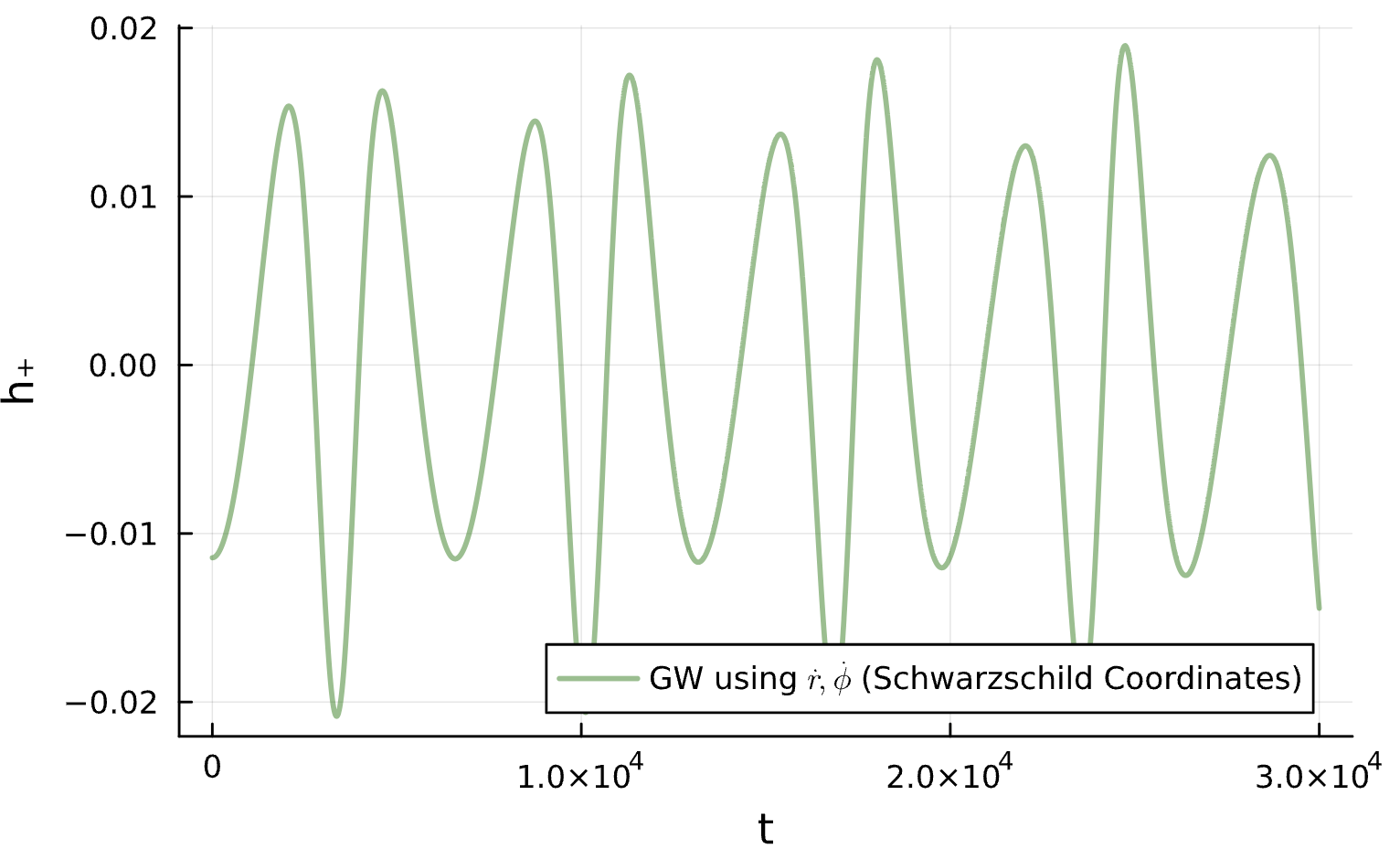
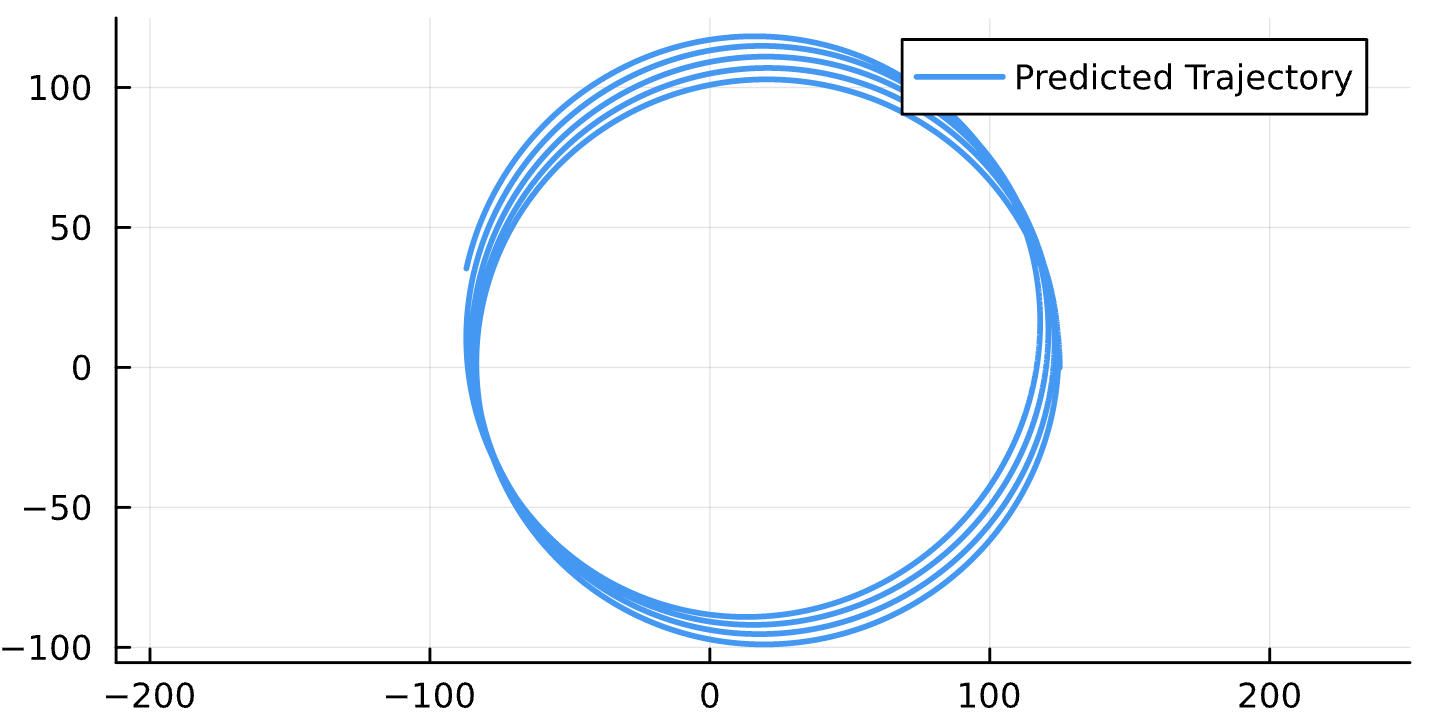
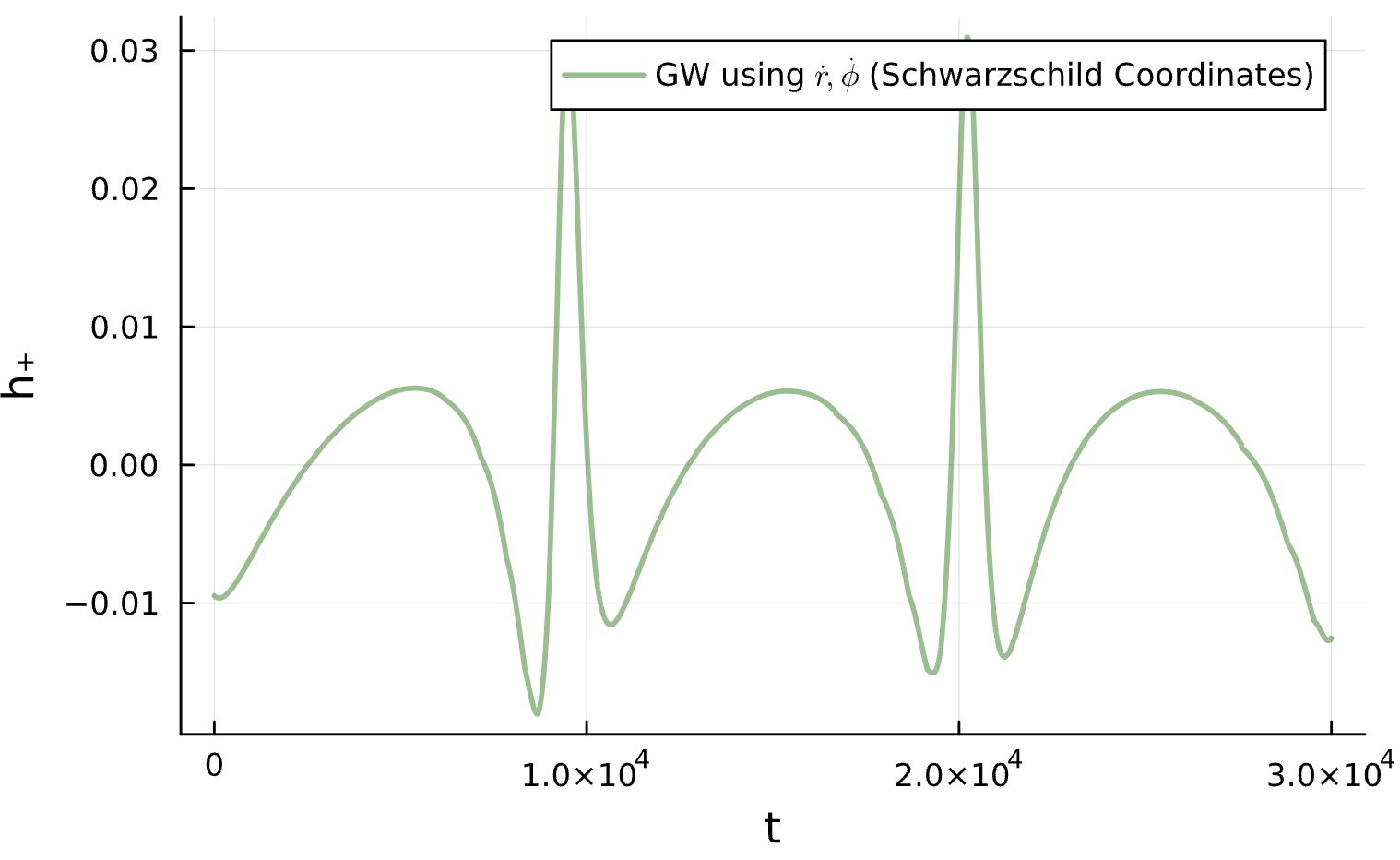
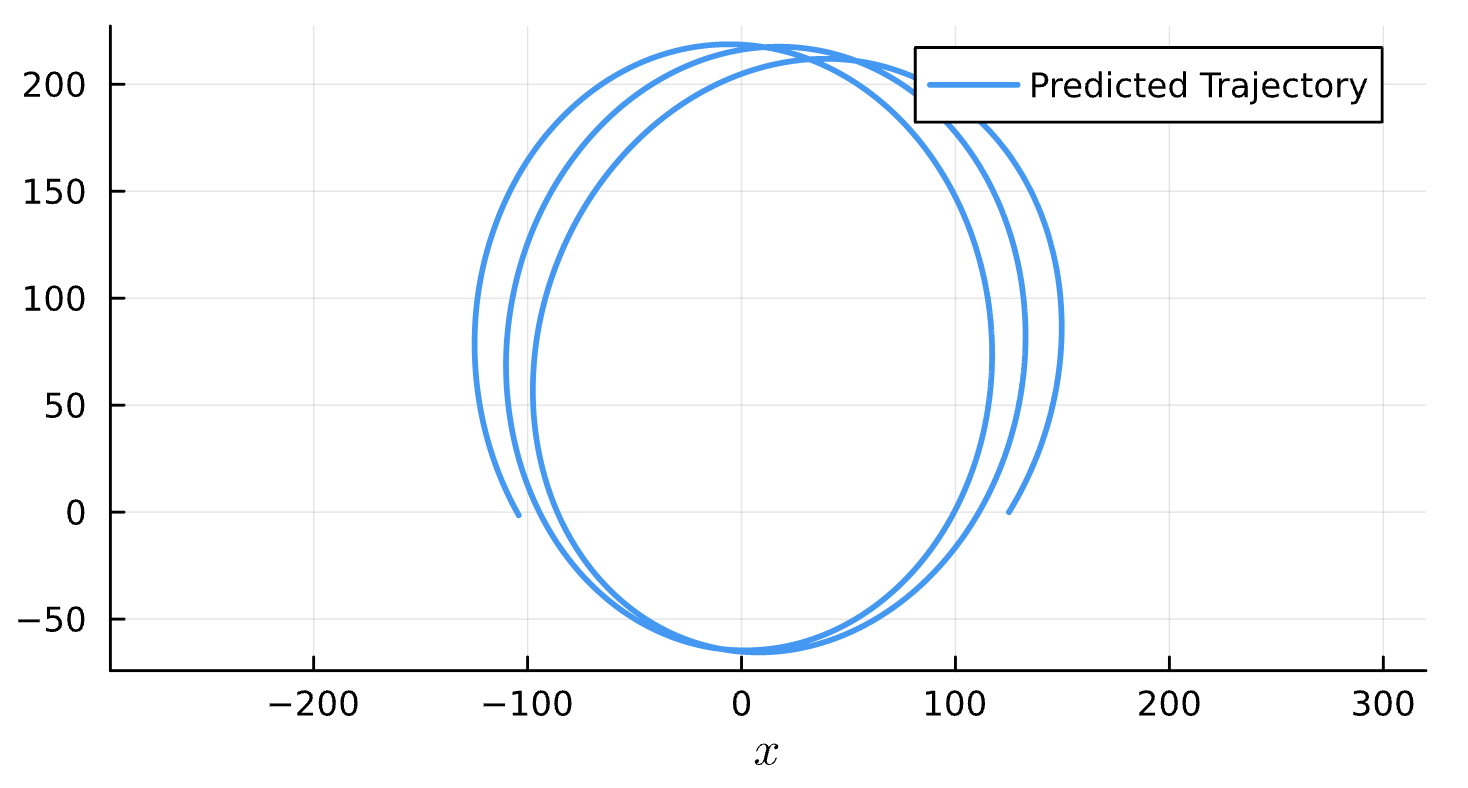
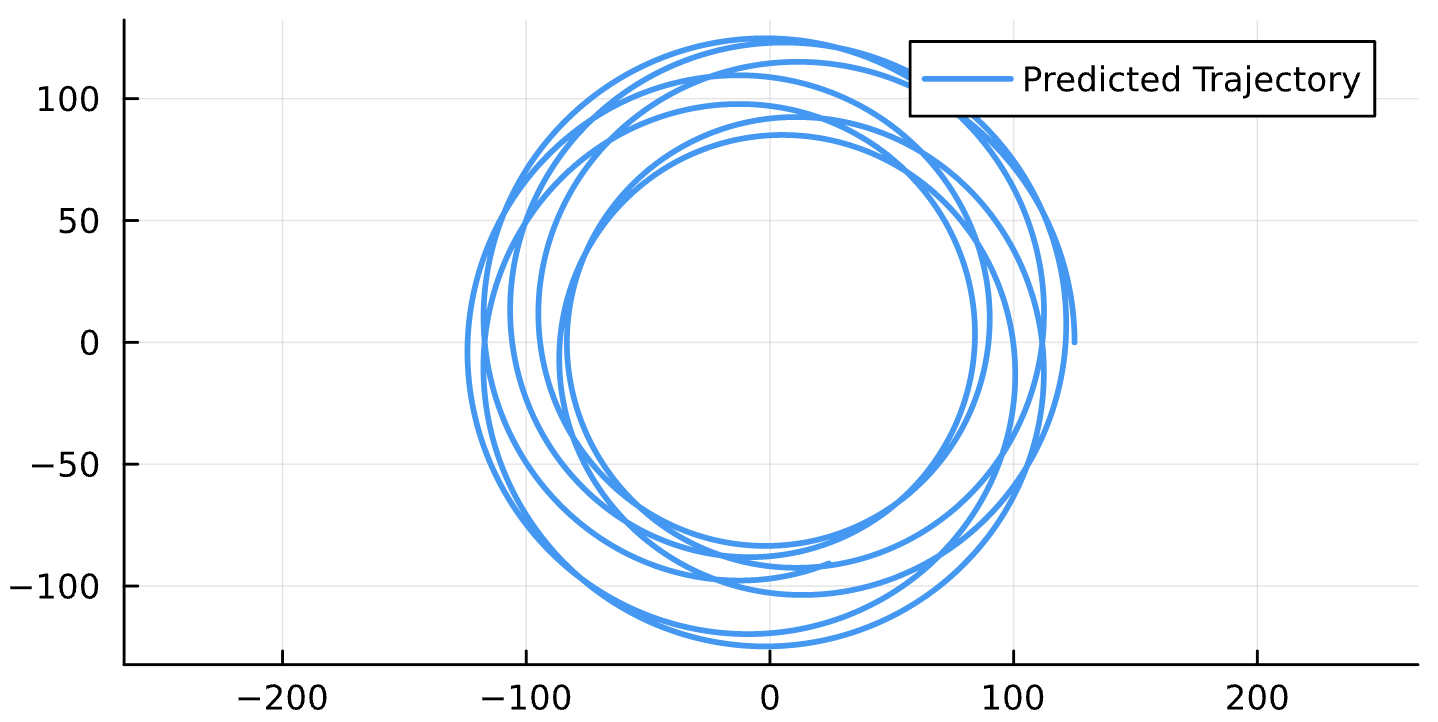
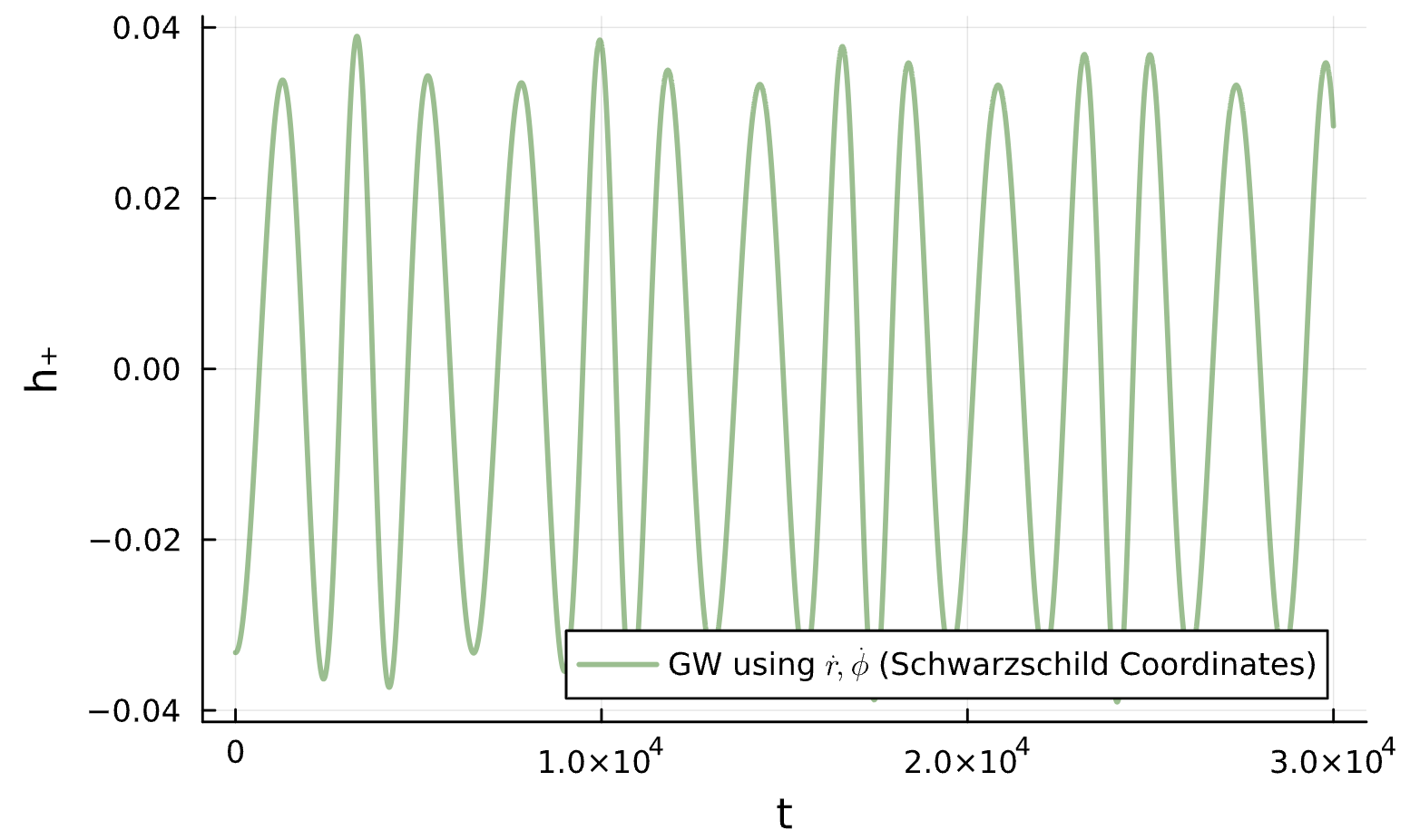
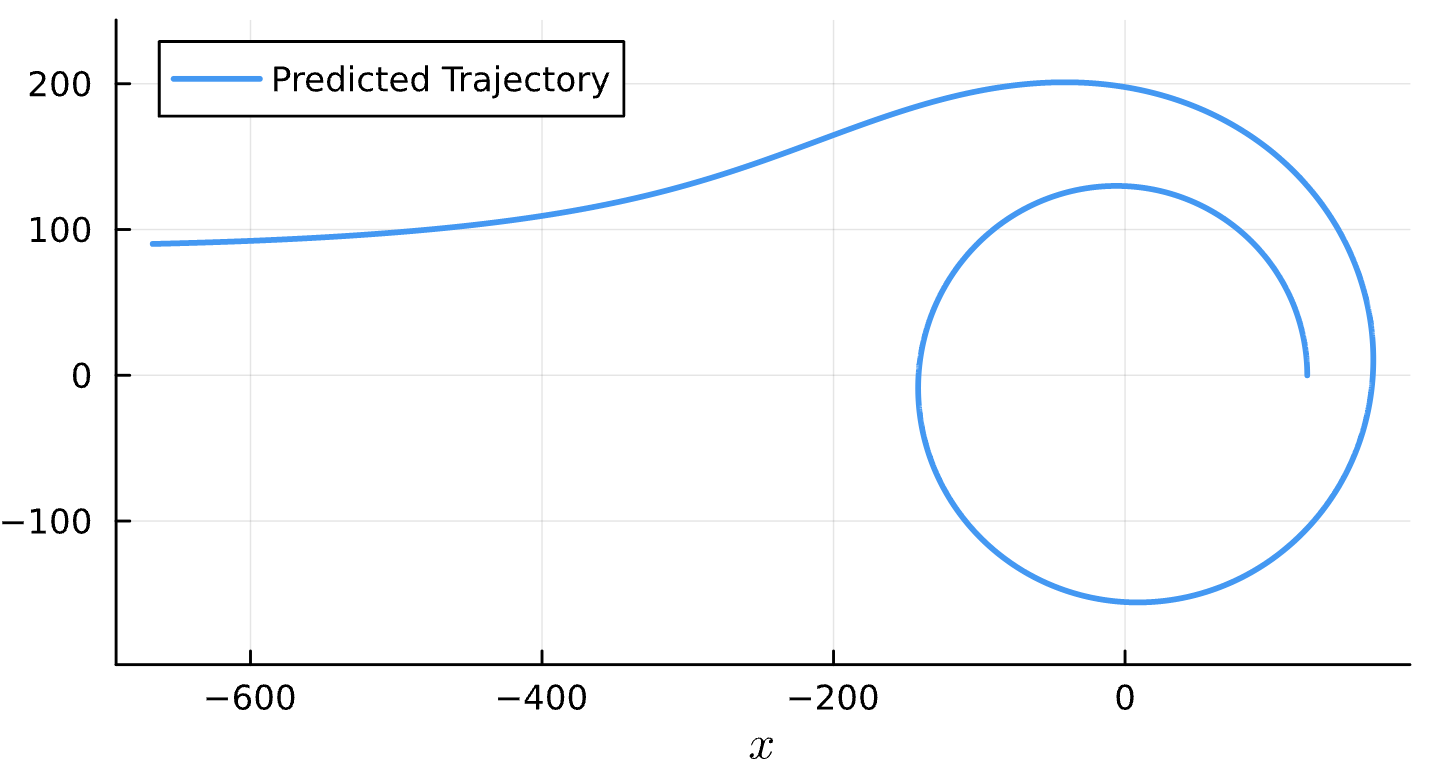
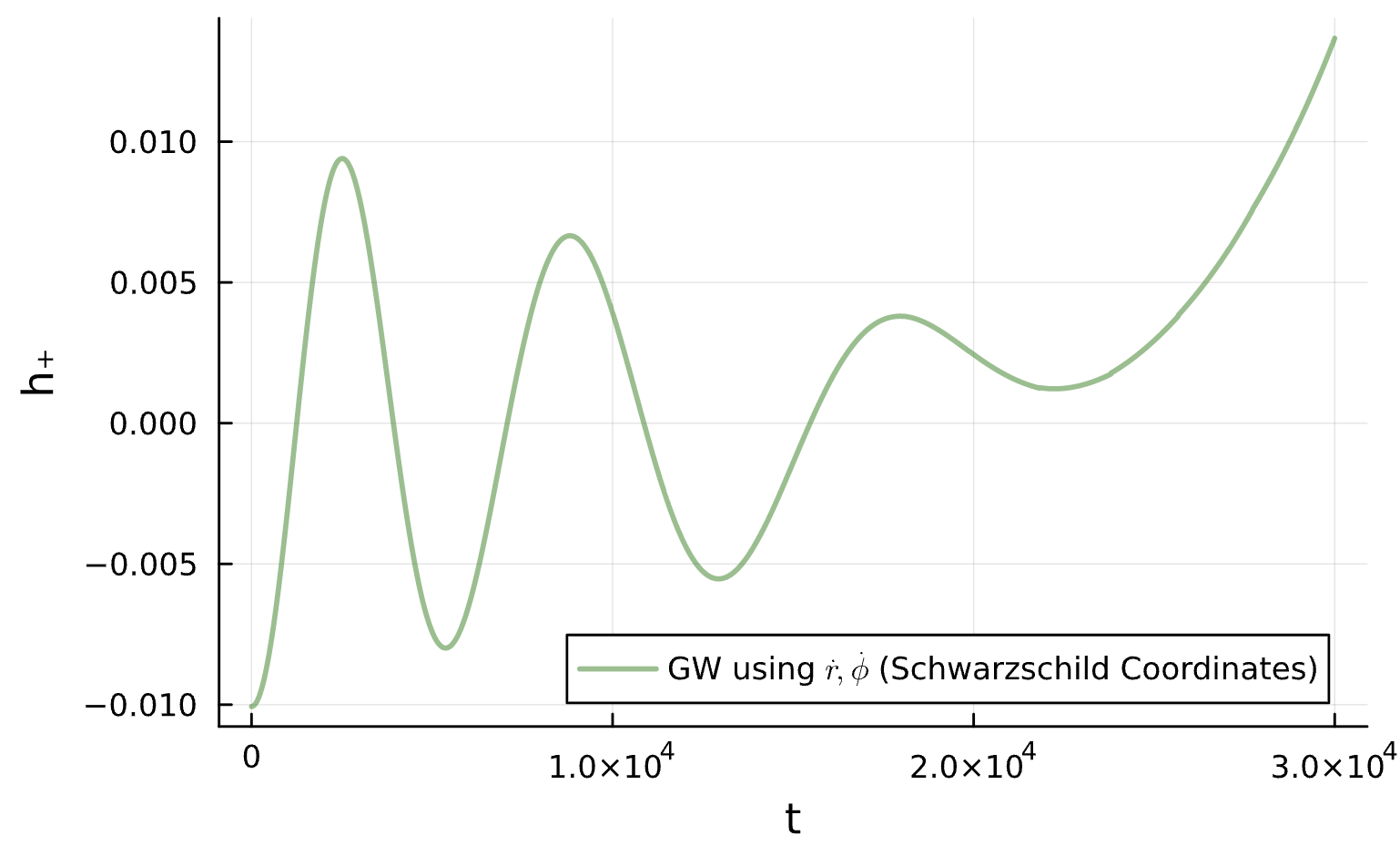
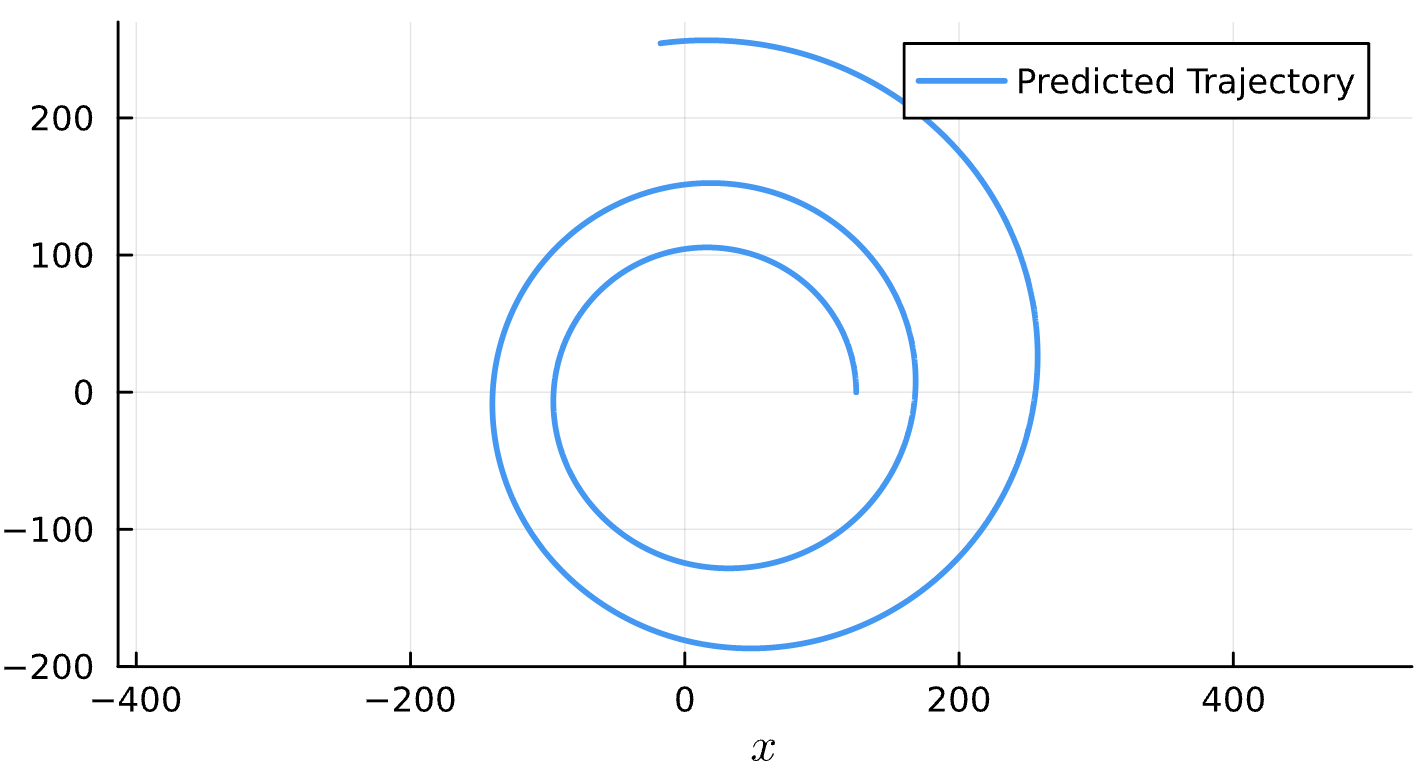
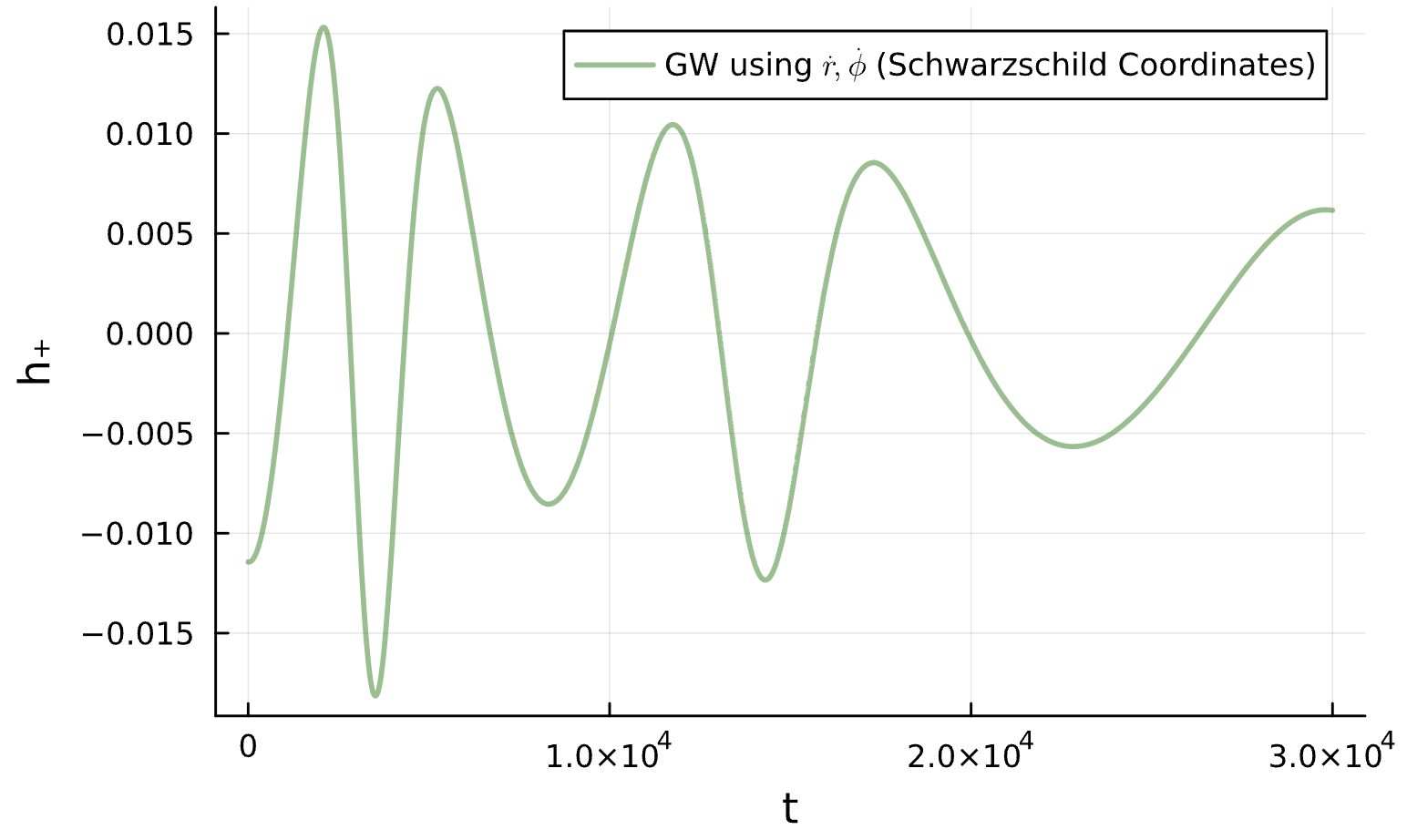
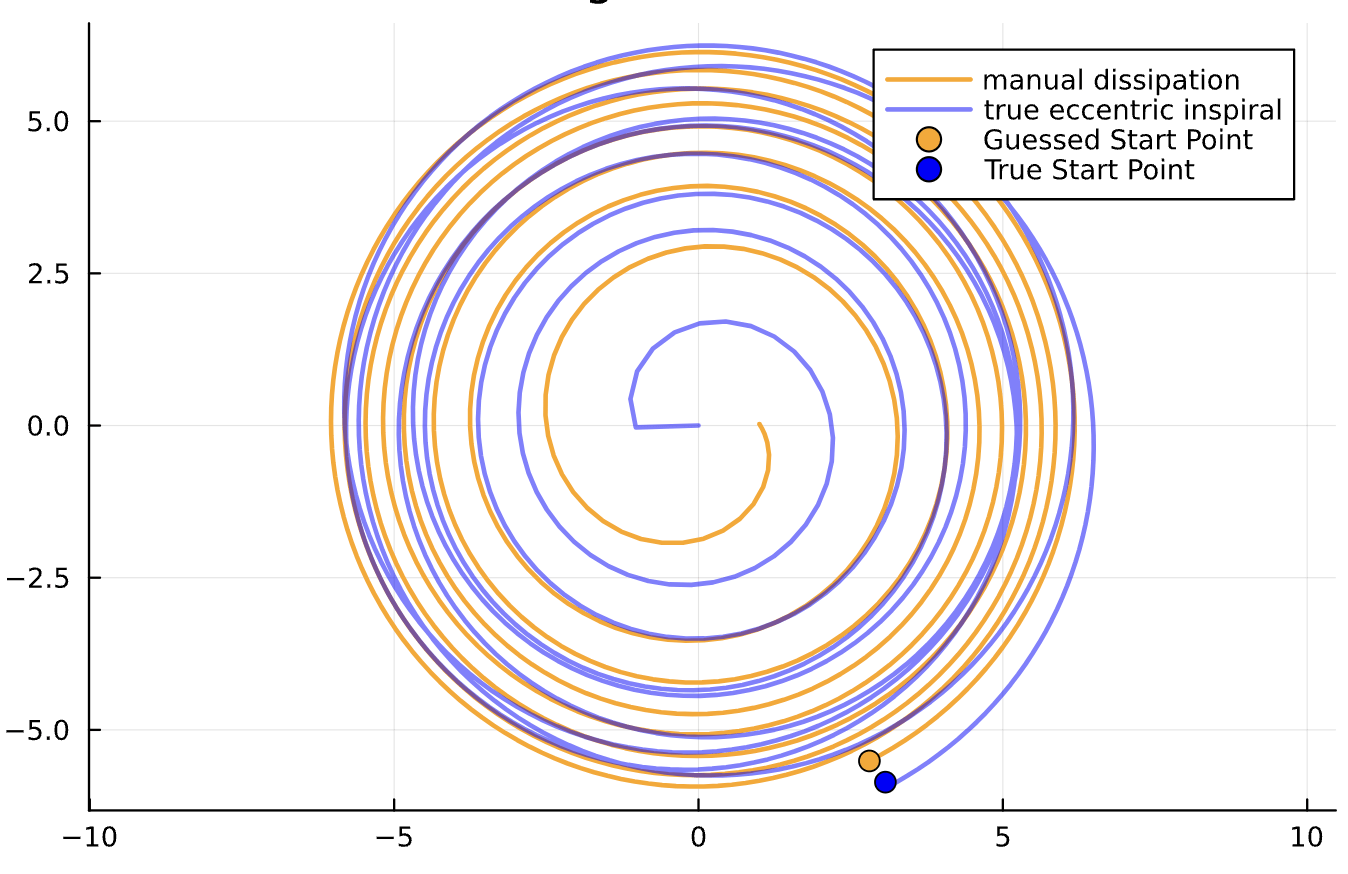
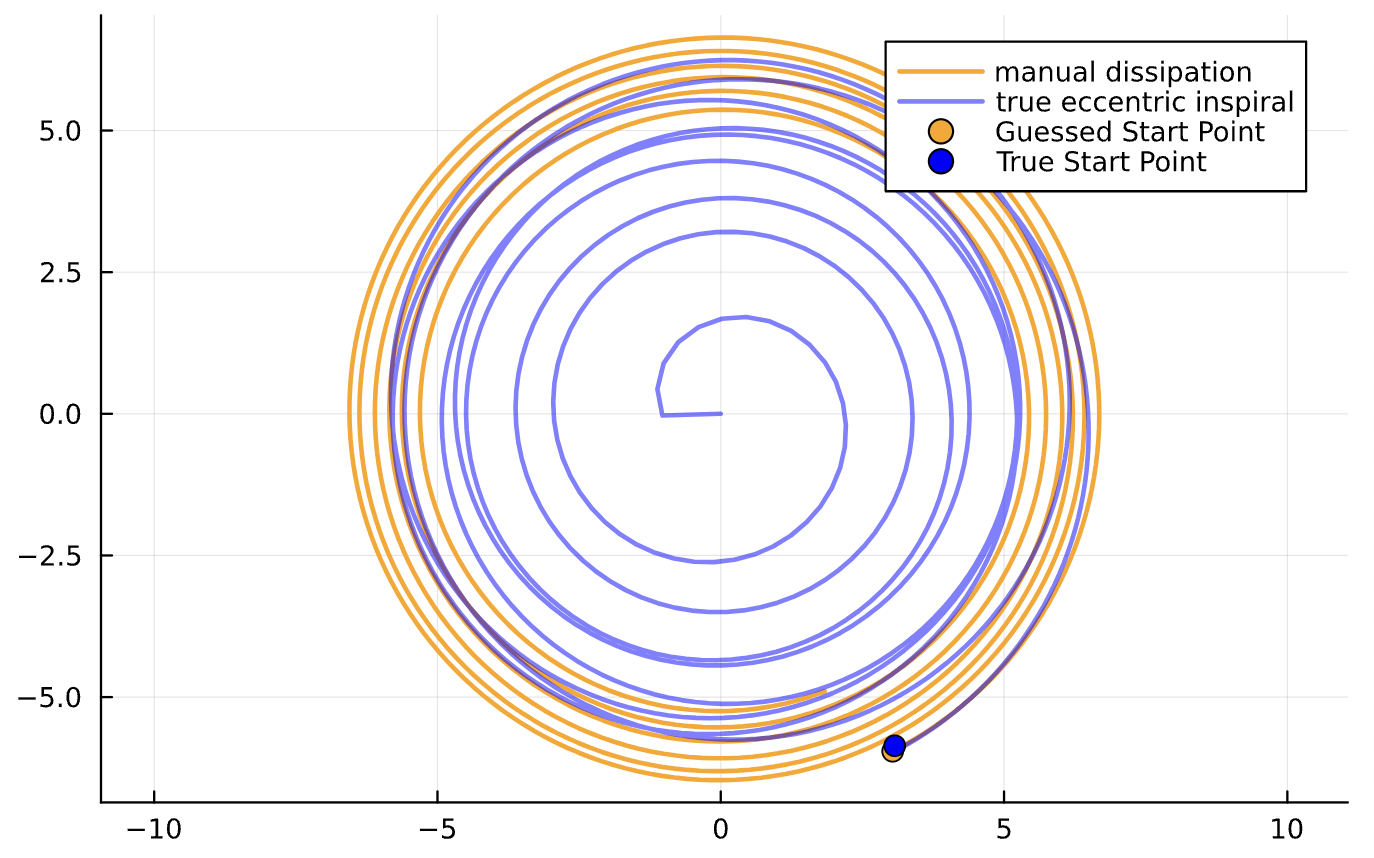
Binary Black Holes
A GENERIC Approach
Ref Bari
Advisor: Prof. Brendan Keith





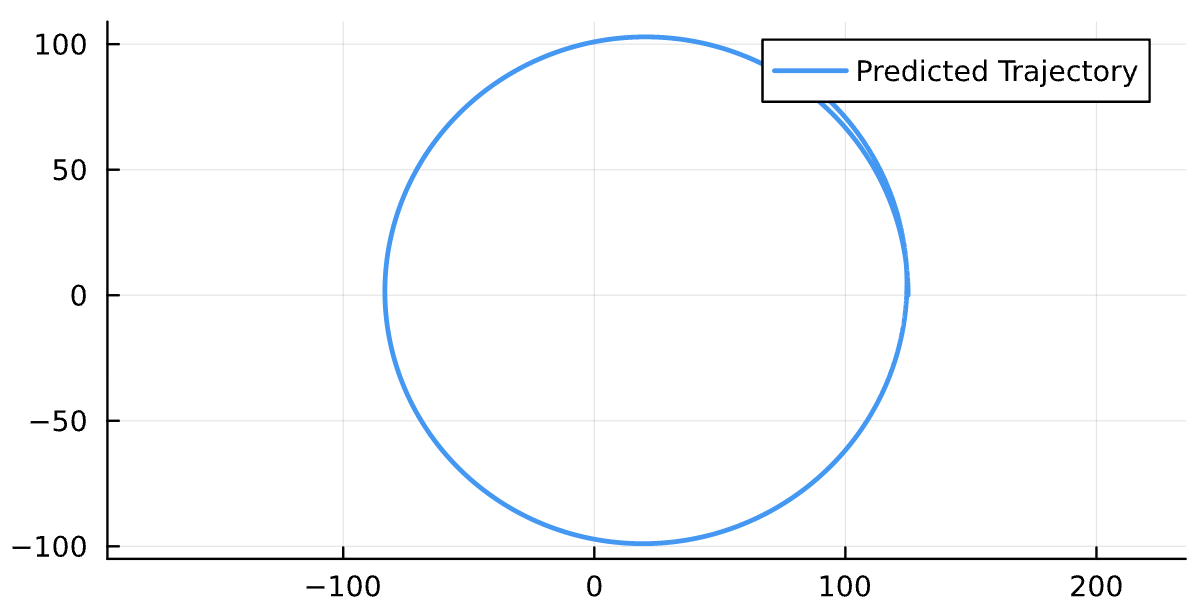
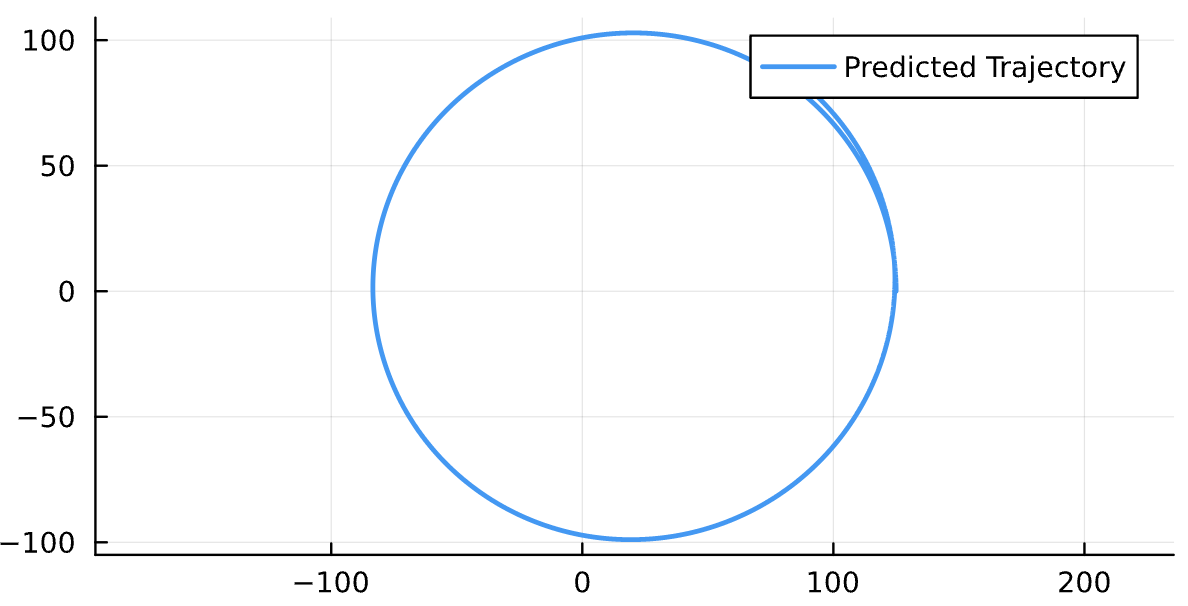
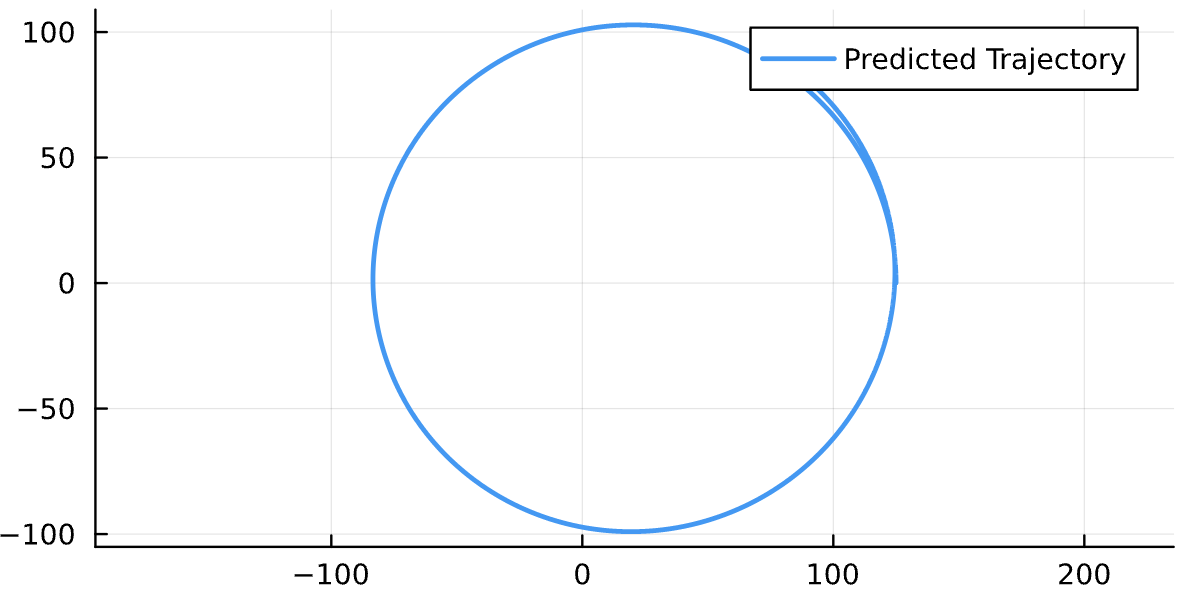
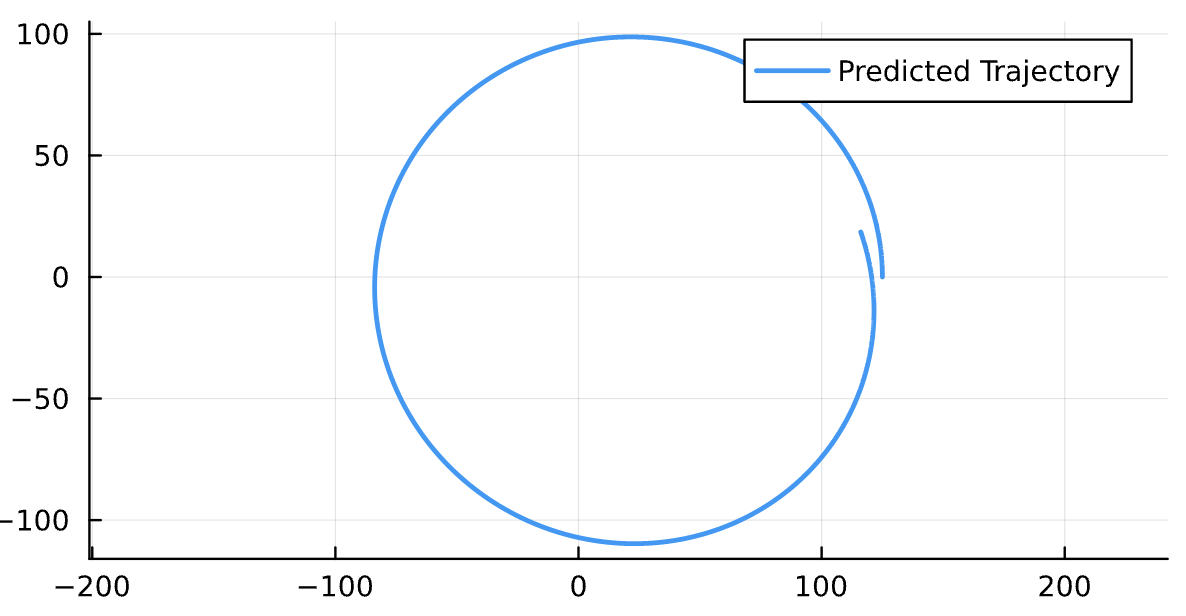
Energy of Particle:
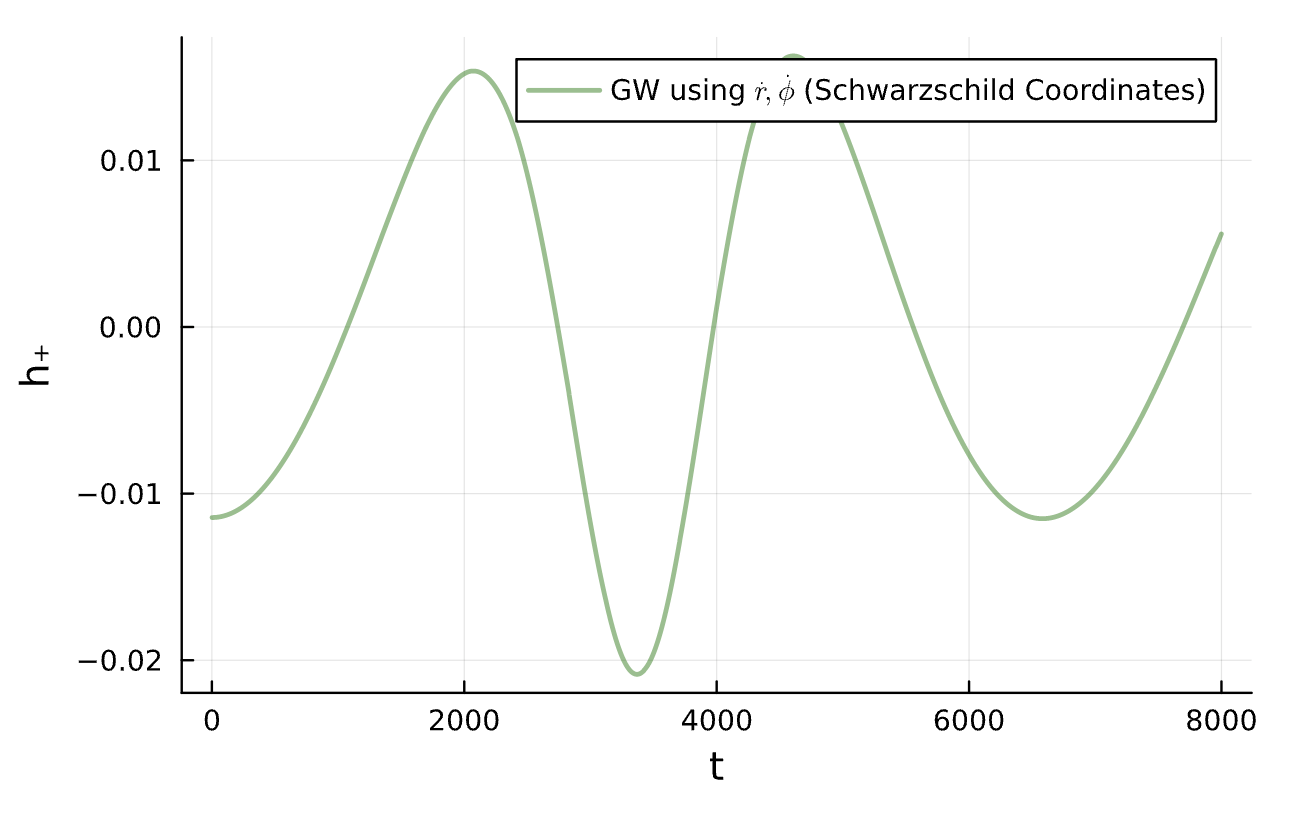
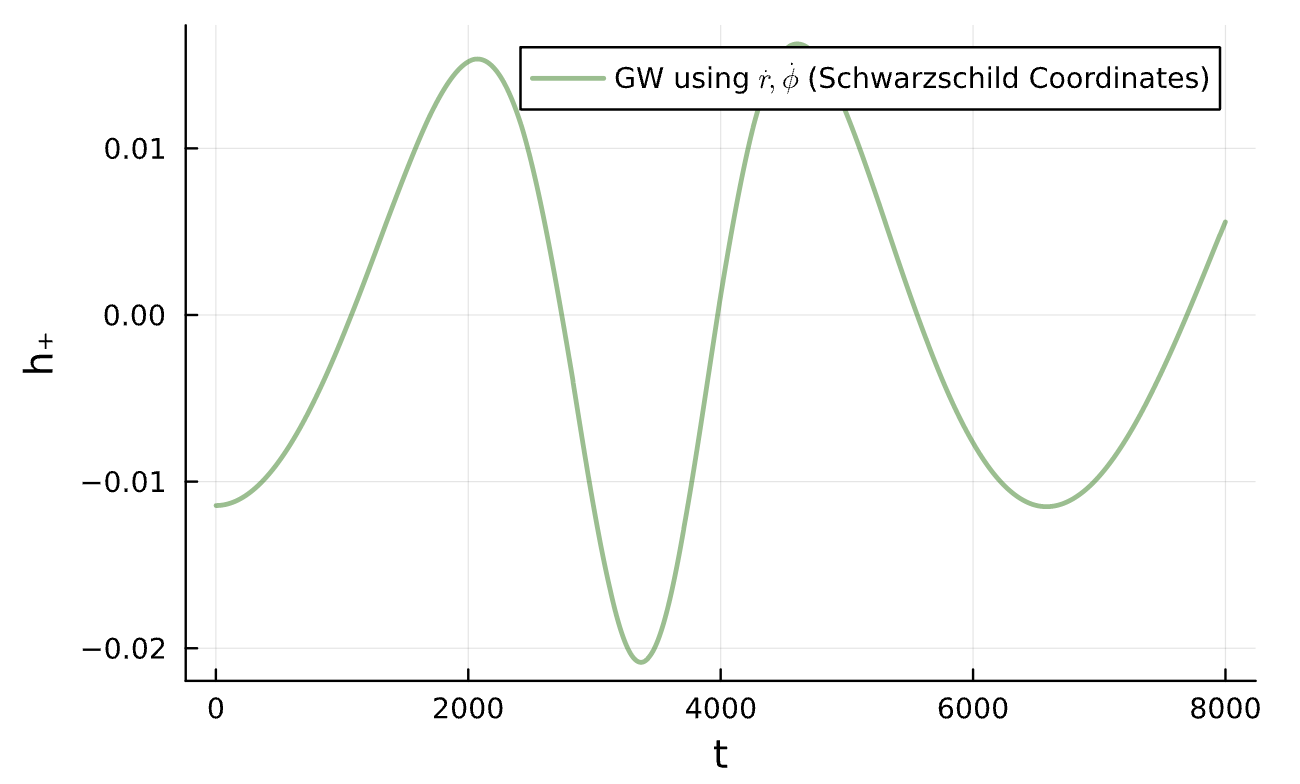
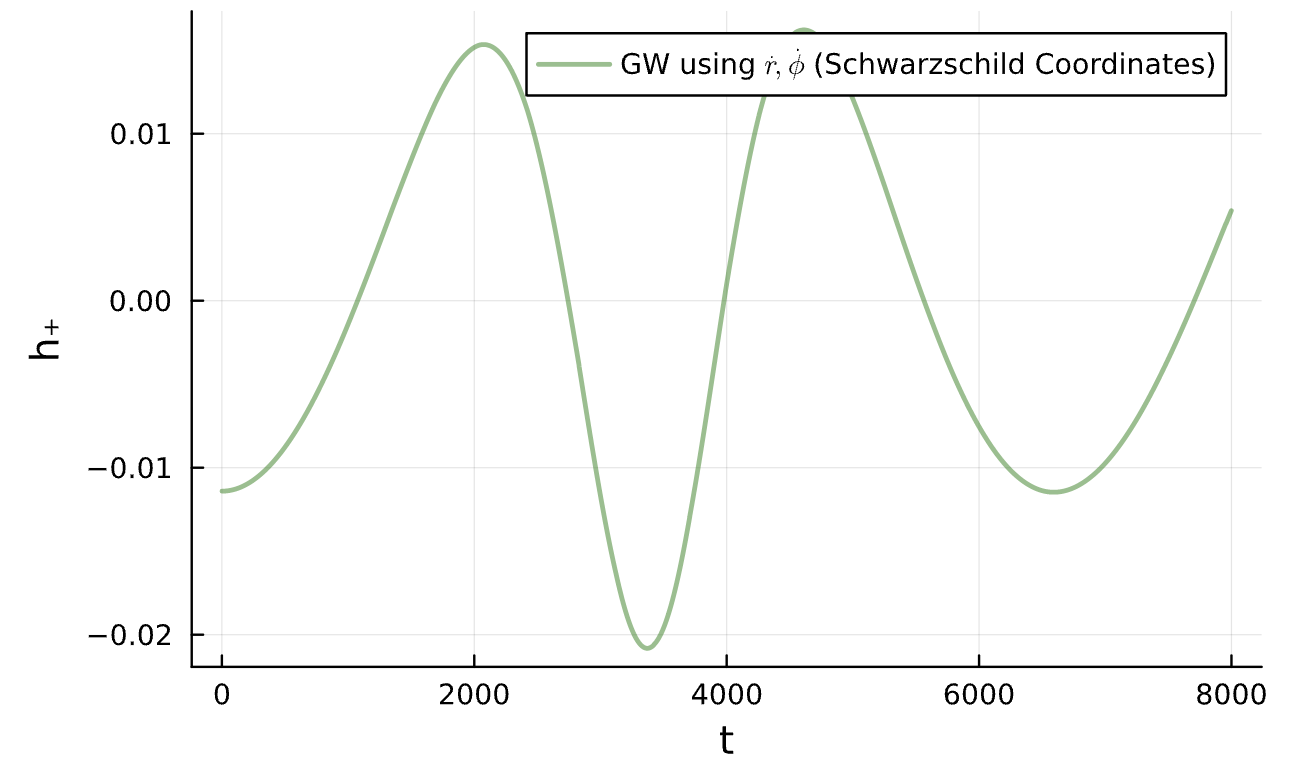
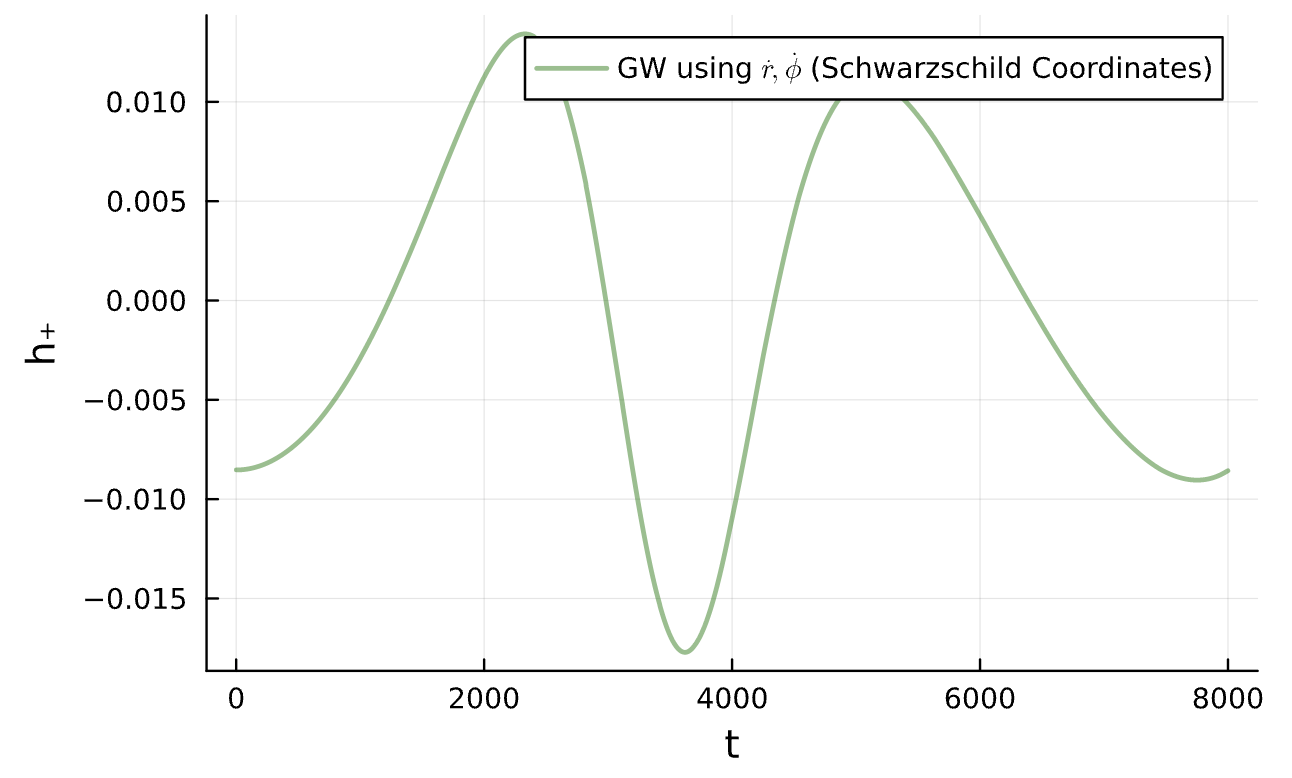
Energy taken away by Gravitational Wave:
| t | h |
|---|---|
| 1.155987123132360184e+00 | -5.609346551357122235e-02 |
| 2.285489553960637910e+00 | -6.036403746984250751e-02 |
| 3.402211606323863879e+00 | -6.318515807196223300e-02 |
| 4.523268886770305031e+00 | -6.485891351192739351e-02 |
| 5.651430592468121183e+00 | -6.641091336216202456e-02 |
Raw SXS Data
2021 SXS Waveform
| t | h |
|---|---|
| 1.155987123132368399e+00 | -5.717062632140130357e-02 |
| 2.285489553960653897e+00 | -6.130264068534922728e-02 |
| 3.402211606323888304e+00 | -6.379464706226181669e-02 |
| 4.523268886770337005e+00 | -6.530329070047019568e-02 |
| 5.651430592468161151e+00 | -6.716188456065923240e-02 |


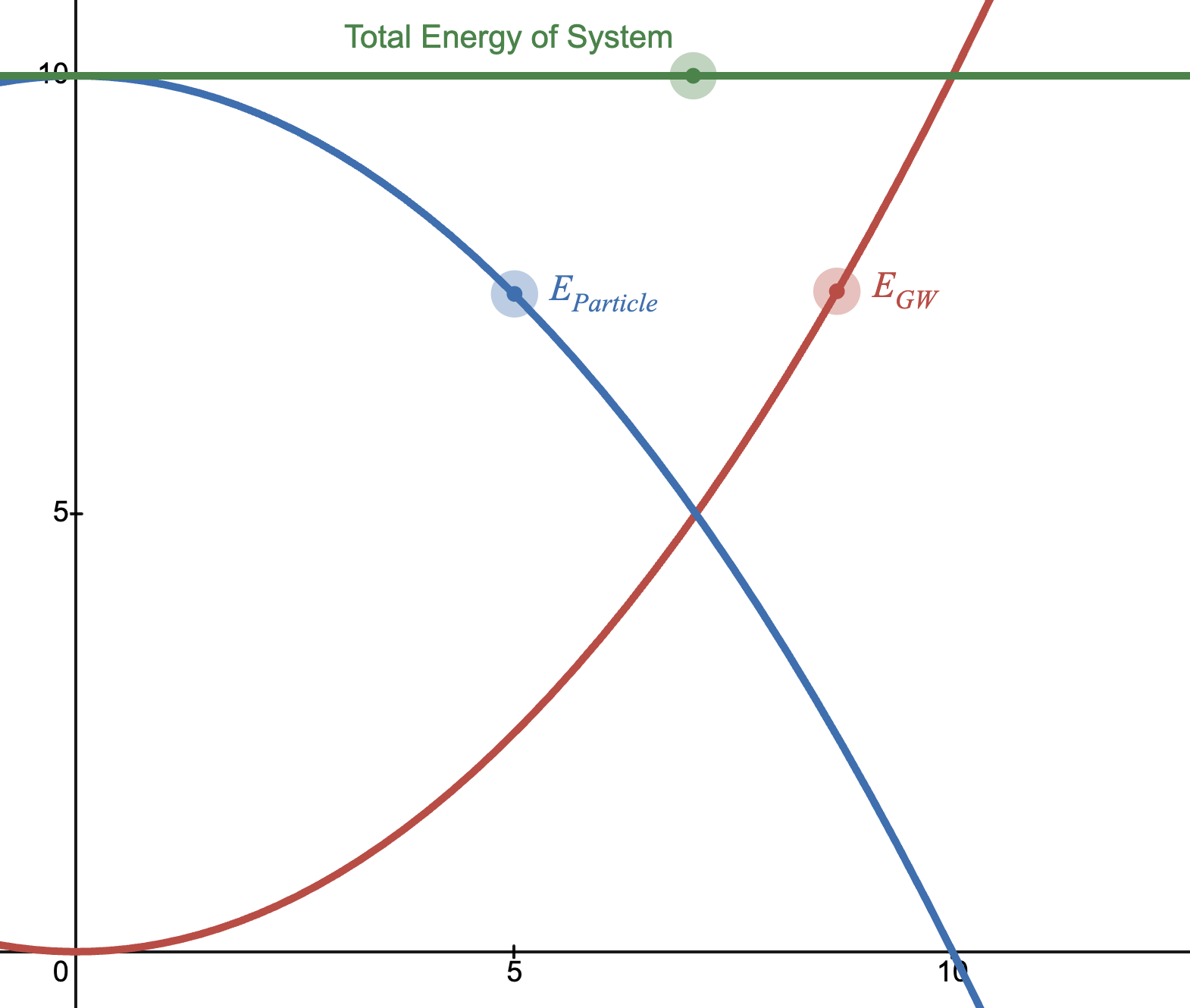
Energy of Particle:
Energy taken away by Gravitational Wave:
Total Energy of System:

Energy of Particle:
Energy taken away by Gravitational Wave:
Total Energy of System:

Energy of Particle:
Energy taken away by Gravitational Wave:
Total Energy of System:

Energy of Particle:
Energy taken away by Gravitational Wave:
GENERIC
What should our energy functional E(x) be?
What should our entropy functional S(x) be?
What should our friction matrix M be?
Should reduce to conservative dynamics if "T=0"
Should conserve the total energy of the closed system
Energy of Particle:
Energy taken away by Gravitational Wave:
Poisson Matrix
Energy Functional
Friction Matrix
Entropy Functional
Energy of Particle:
Energy taken away by Gravitational Wave:
Energy Functional
Friction Matrix
Entropy Functional

L
Energy of Particle:
Energy taken away by Gravitational Wave:
Friction Matrix
Entropy Functional
L

E
Energy of Particle:
Energy taken away by Gravitational Wave:
Entropy Functional
L

E
M
Energy of Particle:
Energy taken away by Gravitational Wave:
L
E
M

S
Energy of Particle:
Energy taken away by Gravitational Wave:
L
E
M

S
Energy of Particle:
Energy taken away by Gravitational Wave:
L
E
M

S
Energy of Particle:
Energy taken away by Gravitational Wave:
L
E
M

S

Energy of Particle:
Energy taken away by Gravitational Wave:
L
E
M

S

Energy of Particle:
Energy taken away by Gravitational Wave:
L
E
M

S

Energy of Particle:
Energy taken away by Gravitational Wave:
L
E
M

S
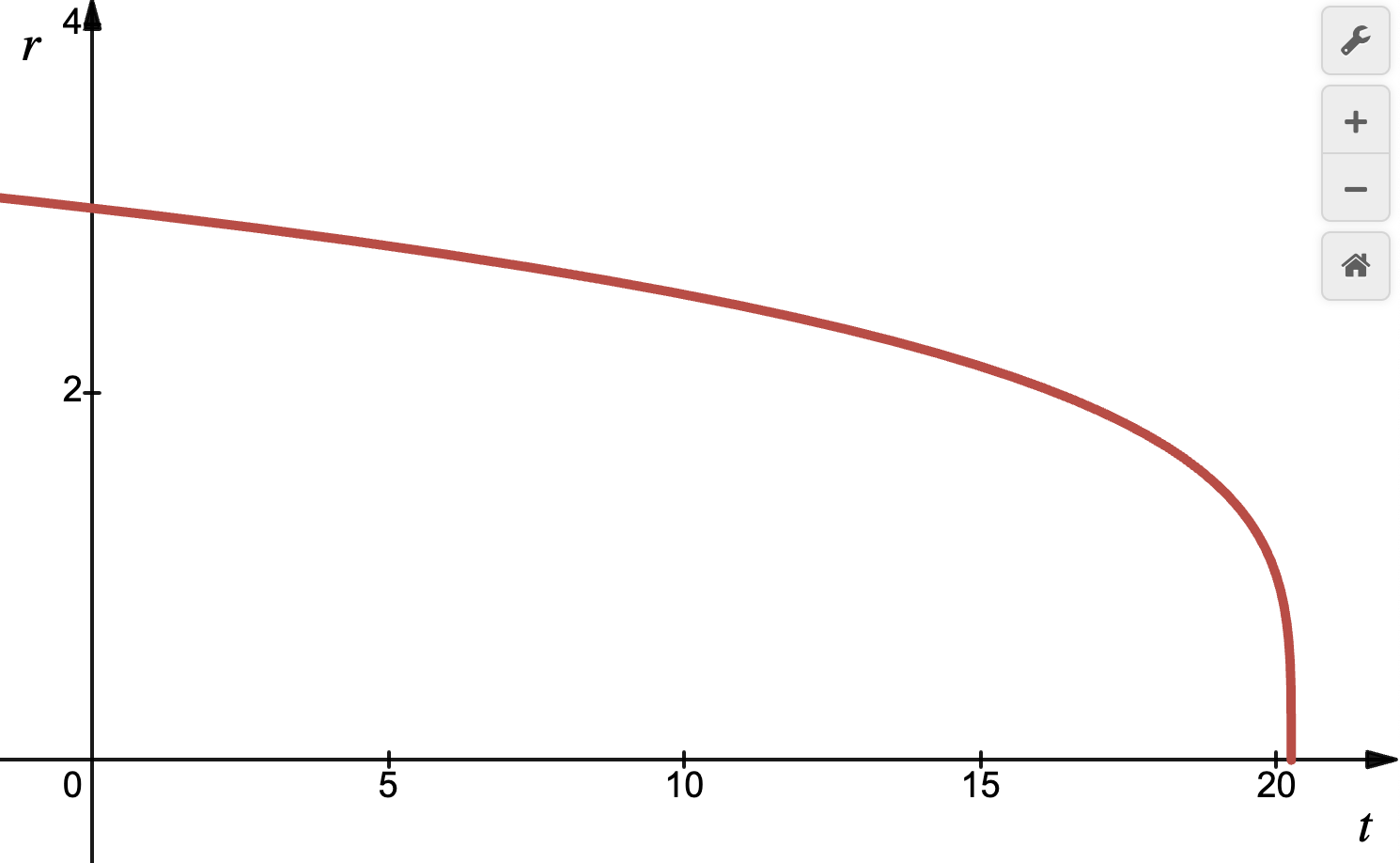
Simplification:
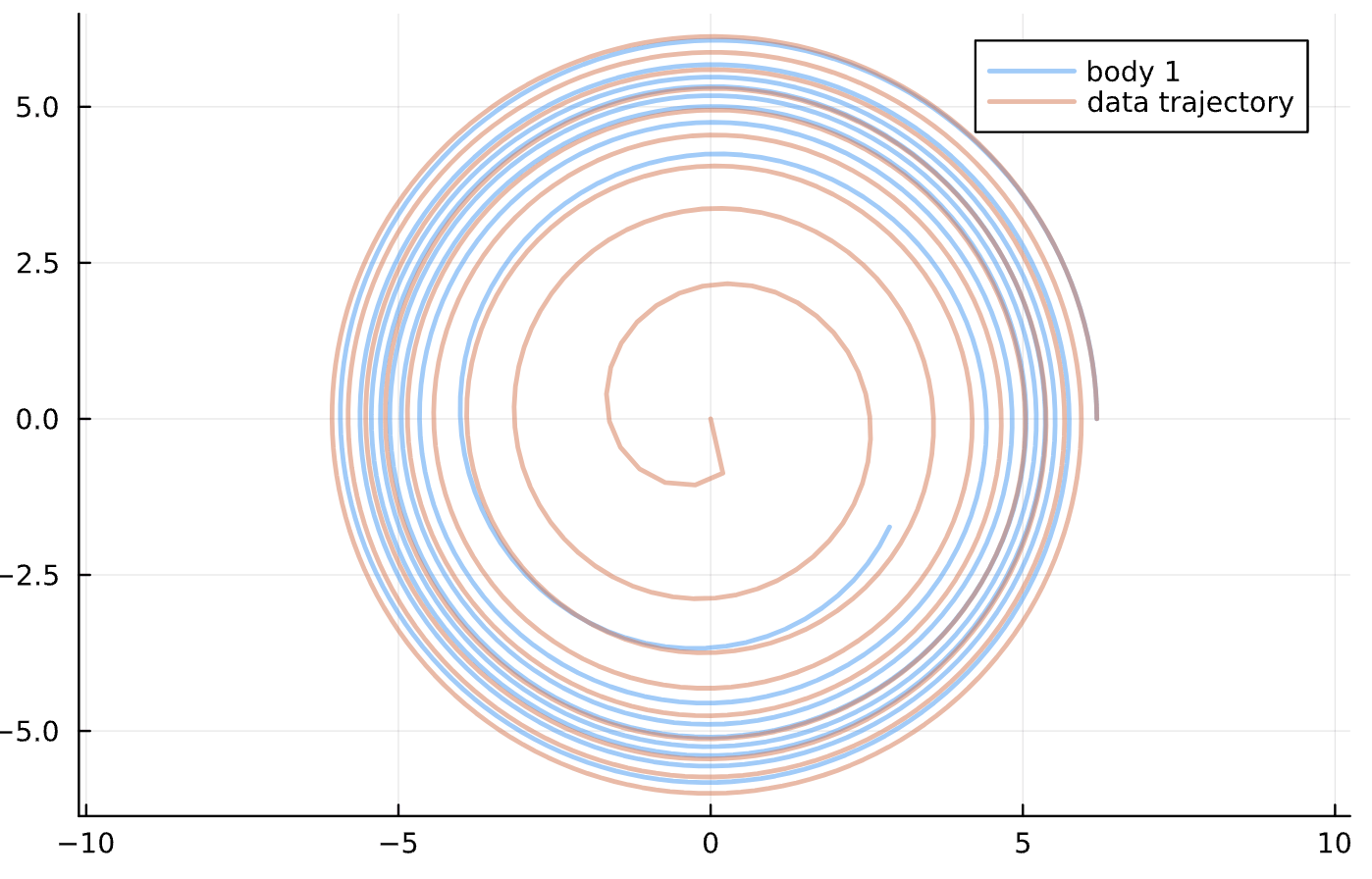
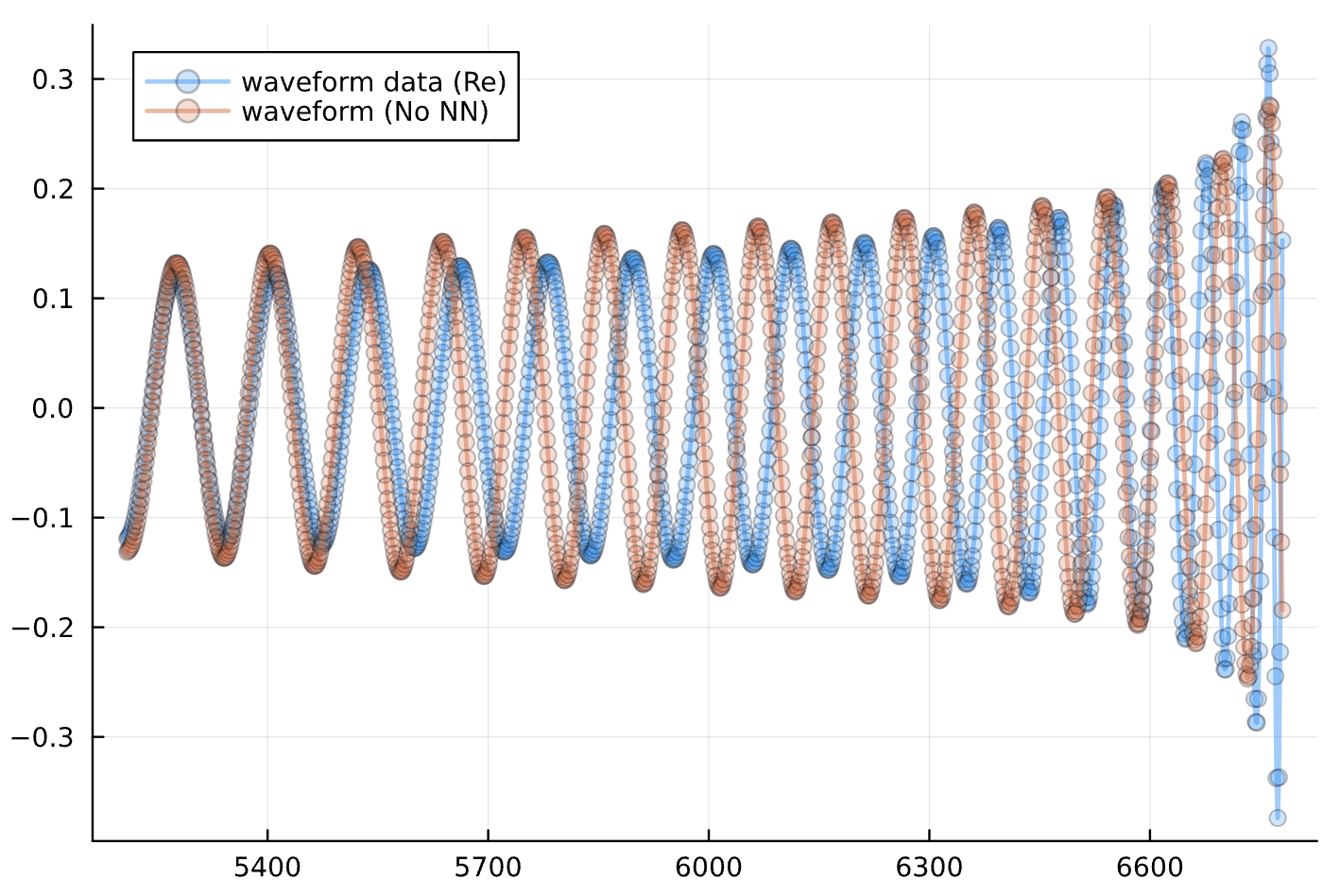


No Neural Network
Neural Network
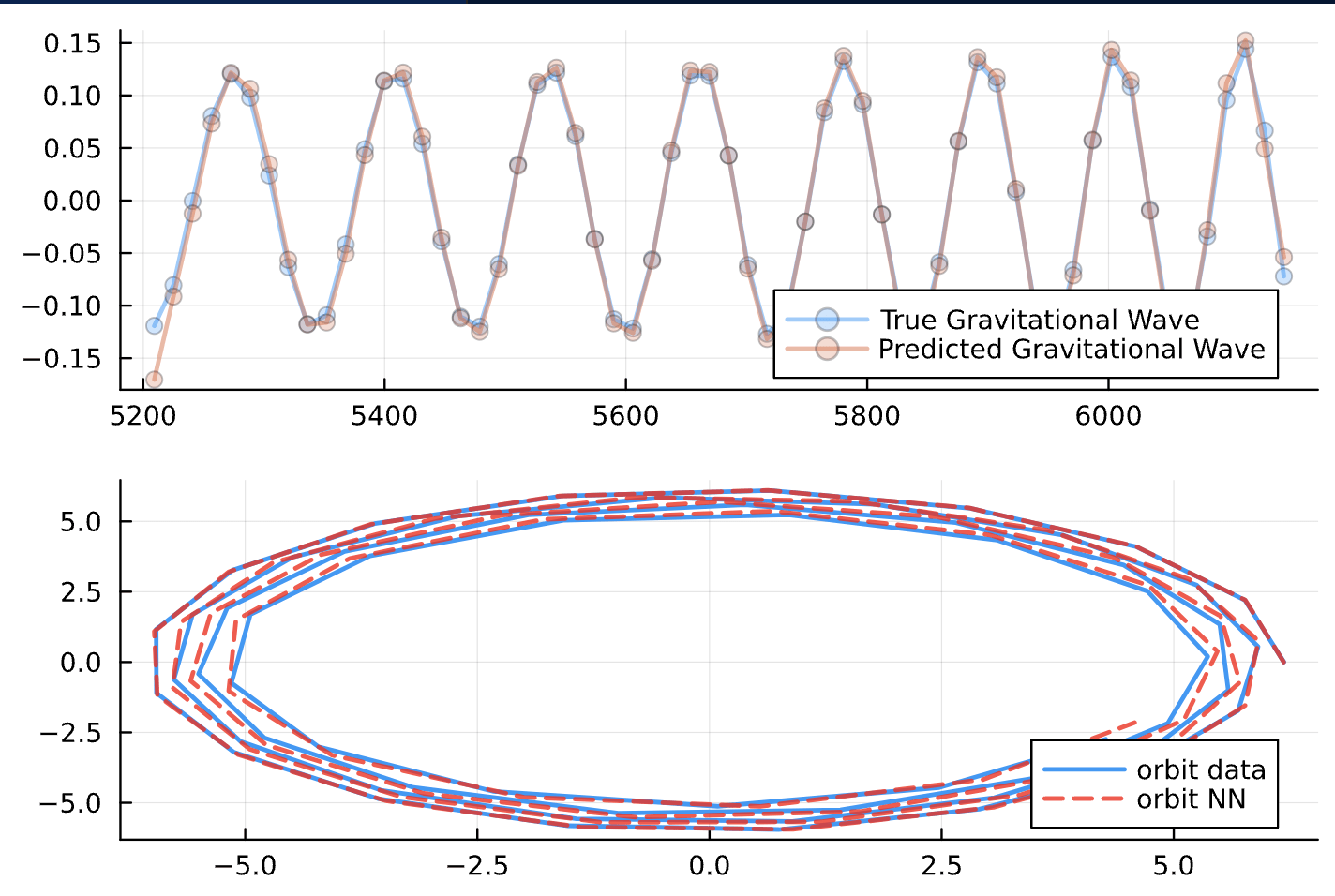
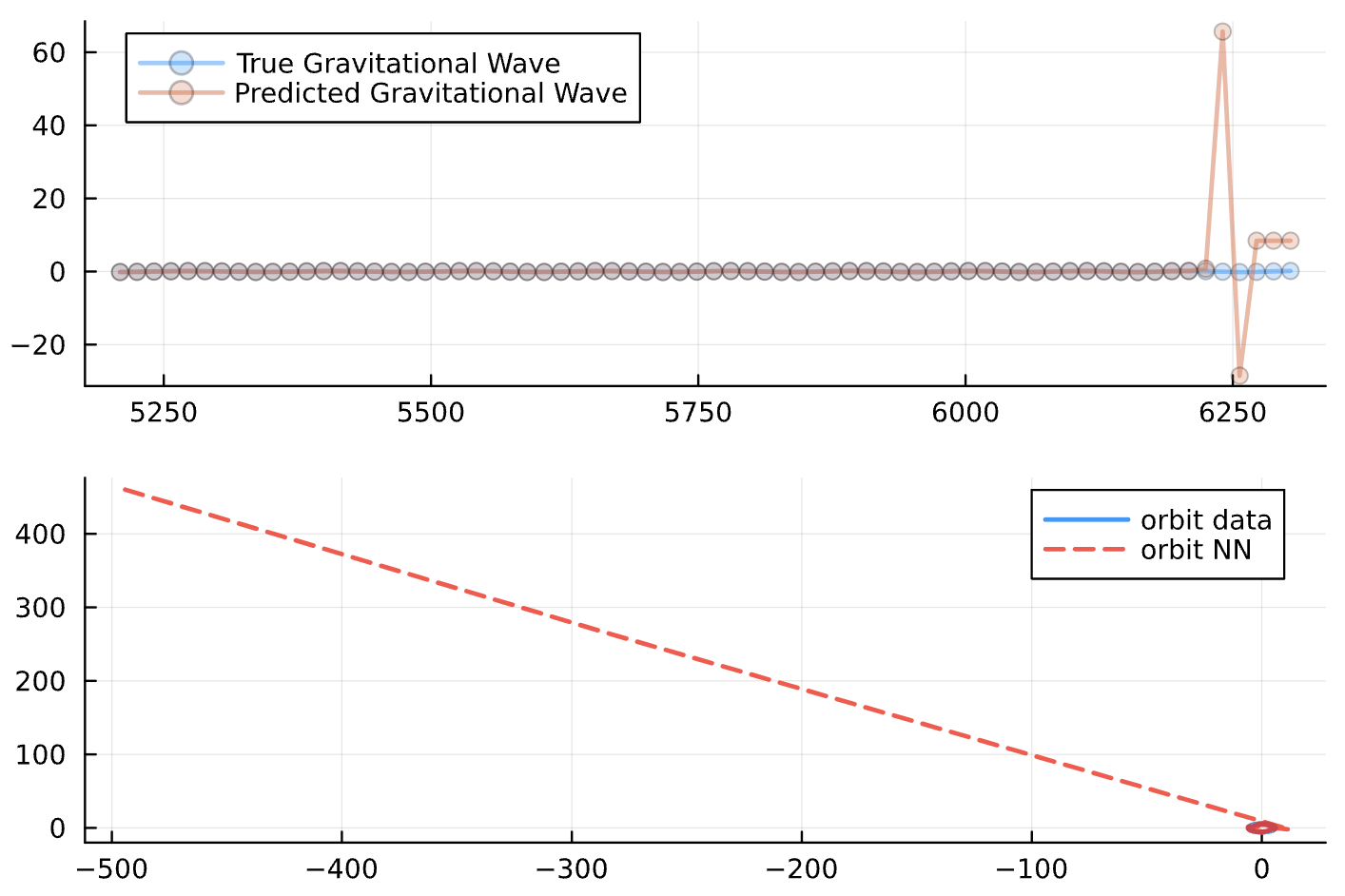
Neural Network
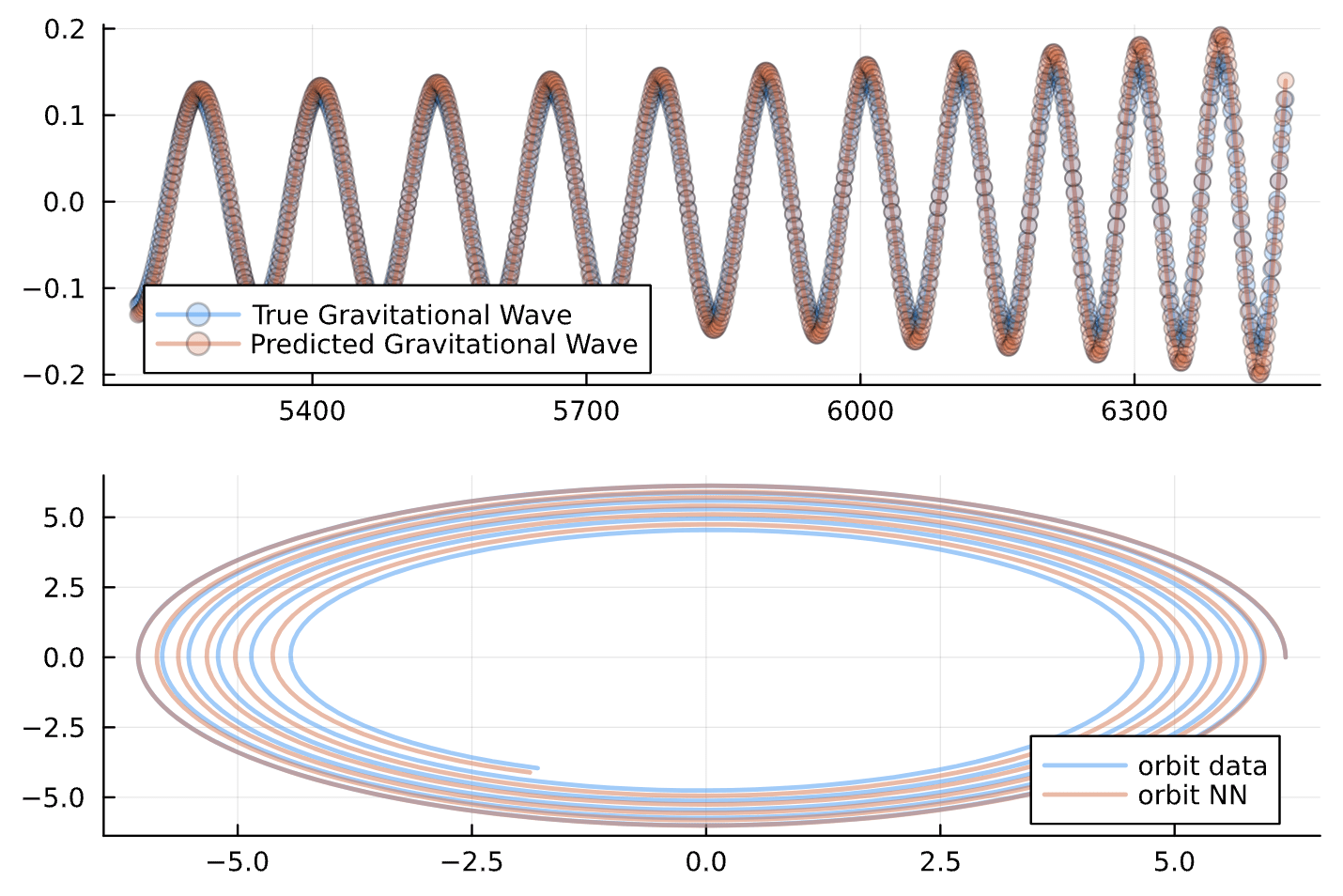
Neural Network
Neural Network
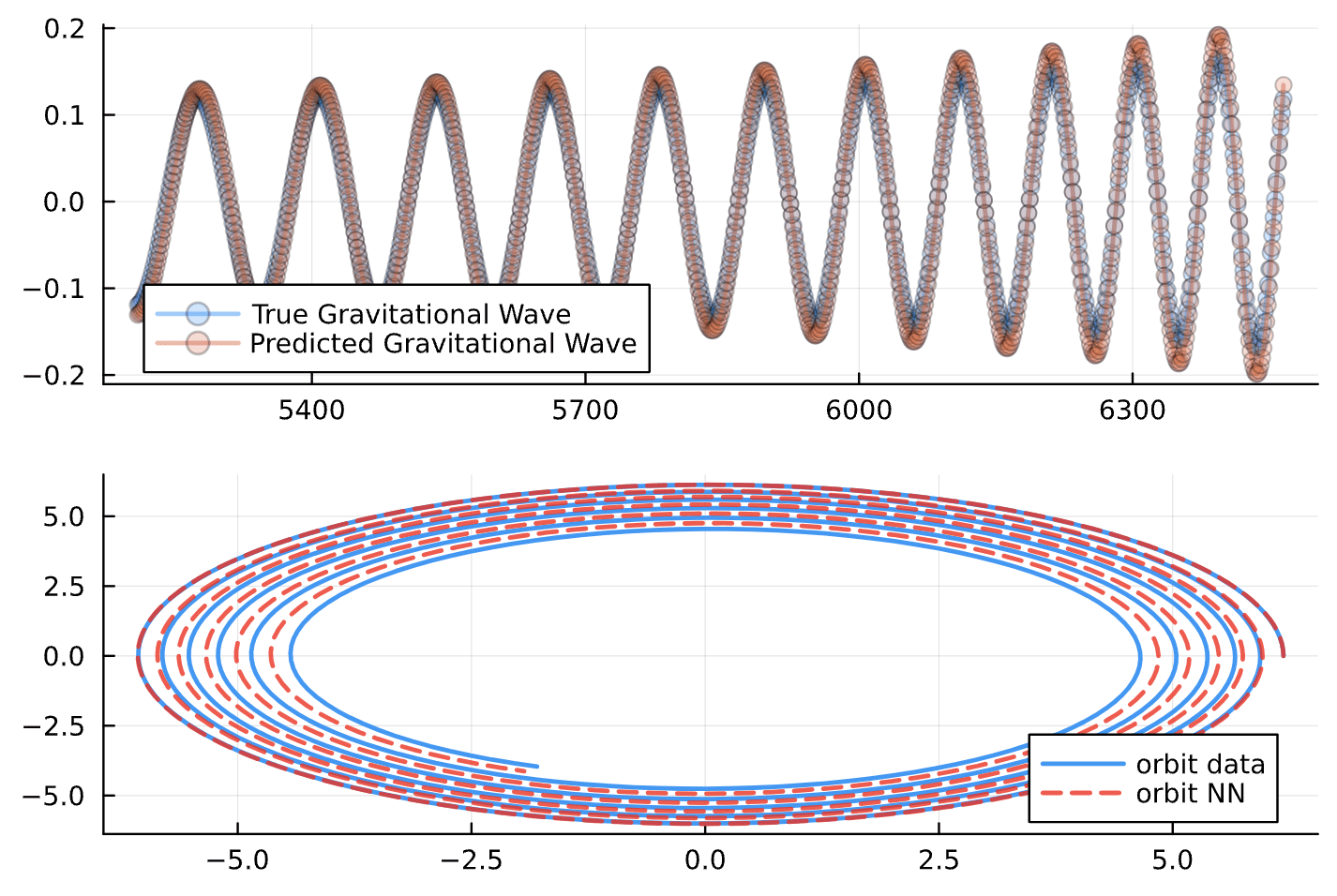
NN = Chain(
Dense(2, 4, tanh),
Dense(4, 4, tanh),
Dense(4, 1),
)M15 = -1 * (250) * (log(1+exp(nn_schwarzschild[1]))) * (1/x[2]^3)Dissipation = [
0, # t
M15, # r
0, # θ
M25, # ϕ
0, # p_t
M35, # p_r
0, # p_θ
M45] # p_ϕdu_dτ = Conservative + DissipationEnergy of Particle:
Energy taken away by Gravitational Wave:
Entropy Functional
L

E
M
Introduction to GENERIC