Bose-Einstein Condensate Black Hole in Low-Earth Orbit
Ref Bari

- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms
- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms

Black Holes play a significant role in the large-scale structure of the universe
The role of black holes in galaxy formation and evolution, A. Cattaneo et. al., 2009 Nature
JWST has recently found galaxies at redshifts z>7 which formed unexpectedly early -- one emerging explanation is primordial BHs facilitated rapid growth of these early galaxies
Rapidly growing primordial black holes as seeds of the massive high-redshift JWST Galaxies, Yuan et. al., 2024

The event horizon of a BH is the surface of no return

The event horizon of a BH is the surface of no return

A singularity at r = 2GM!
The event horizon of a BH is the surface of no return

Area Theorem for Event Horizons (1971, Hawking):

The total area of event horizons cannot decrease
Entropy of Black Holes (Bekenstein, 1972)
Which results in the second law of black hole thermodynamics:
Entropy of Black Holes (Bekenstein, 1972)
Which results in the second law of black hole thermodynamics:
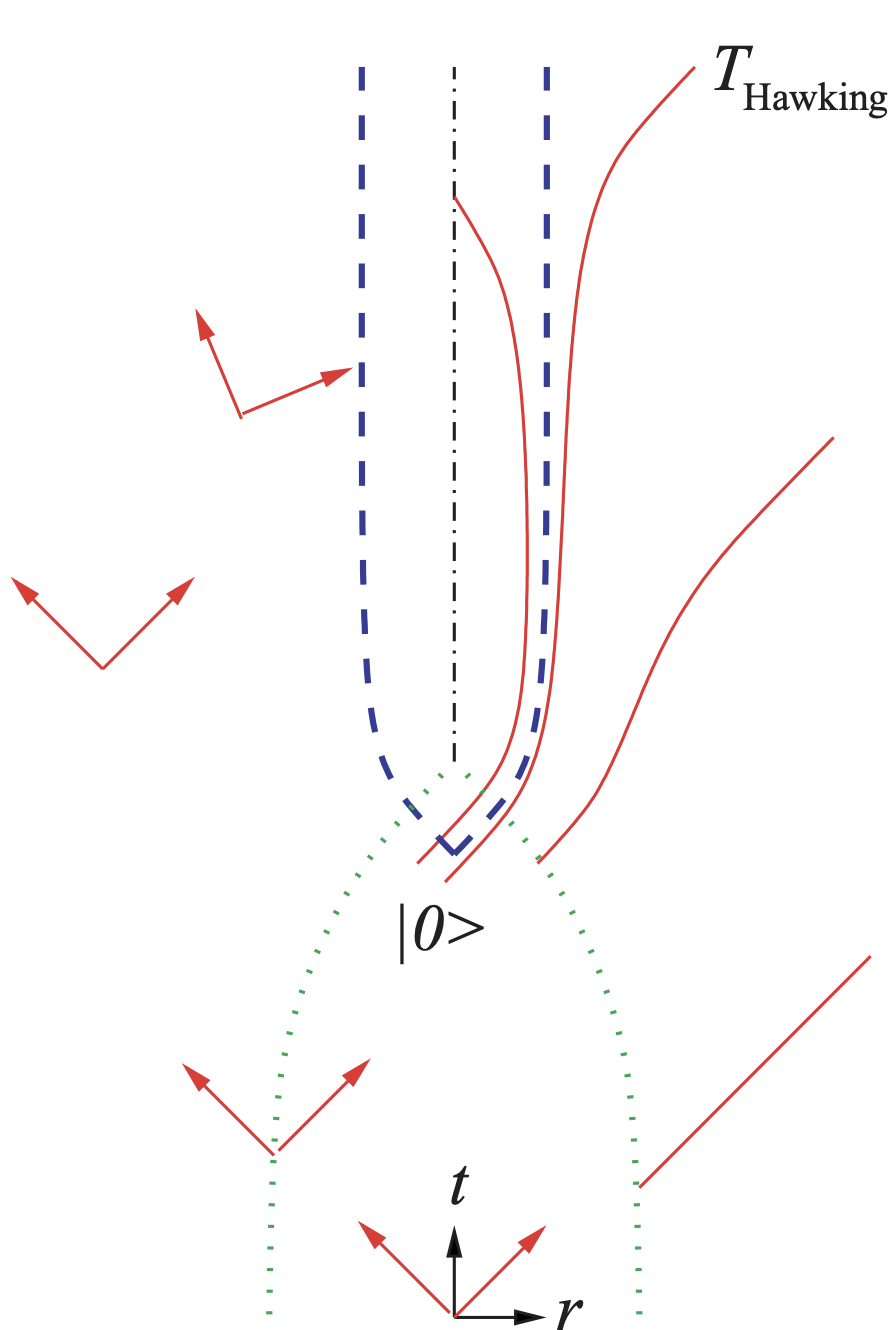
But this implies that black holes must have a temperature!
Entropy of Black Holes (Bekenstein, 1972)
Which results in the second law of black hole thermodynamics:
But this implies that black holes must have a temperature!
As they evaporate, BHs lose area! But second law still holds, because Hawking Radiation increases dS to compensate!
- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms
- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms
1926

1995
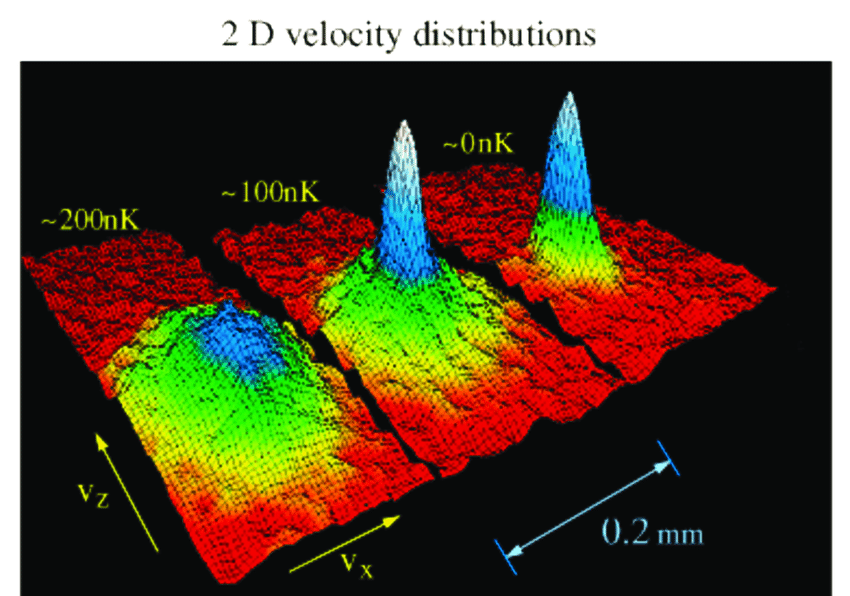




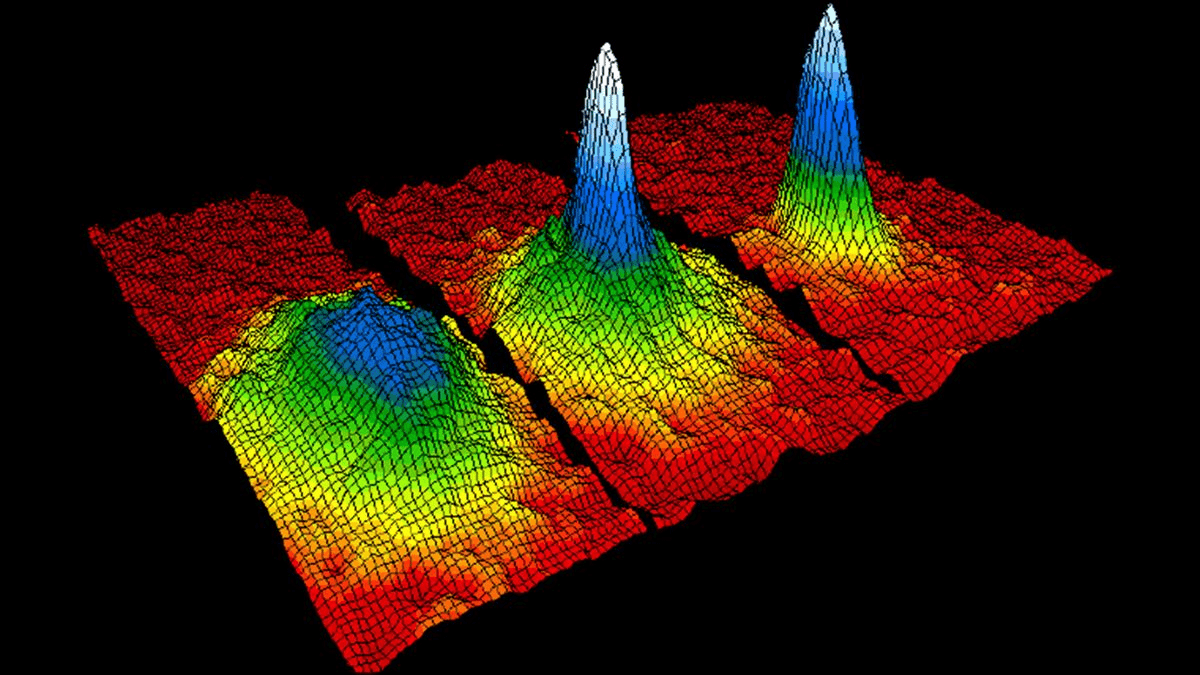






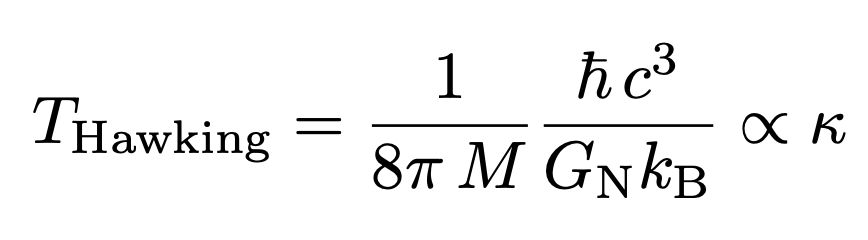
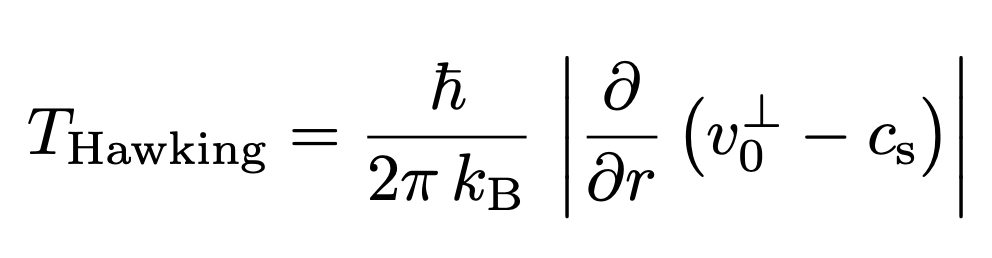
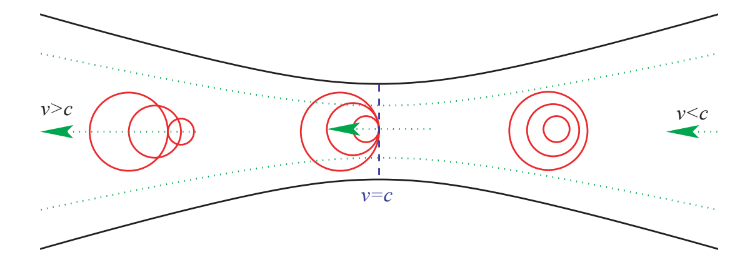
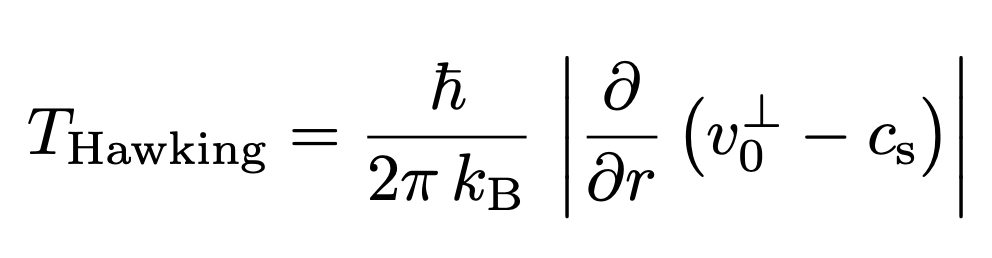
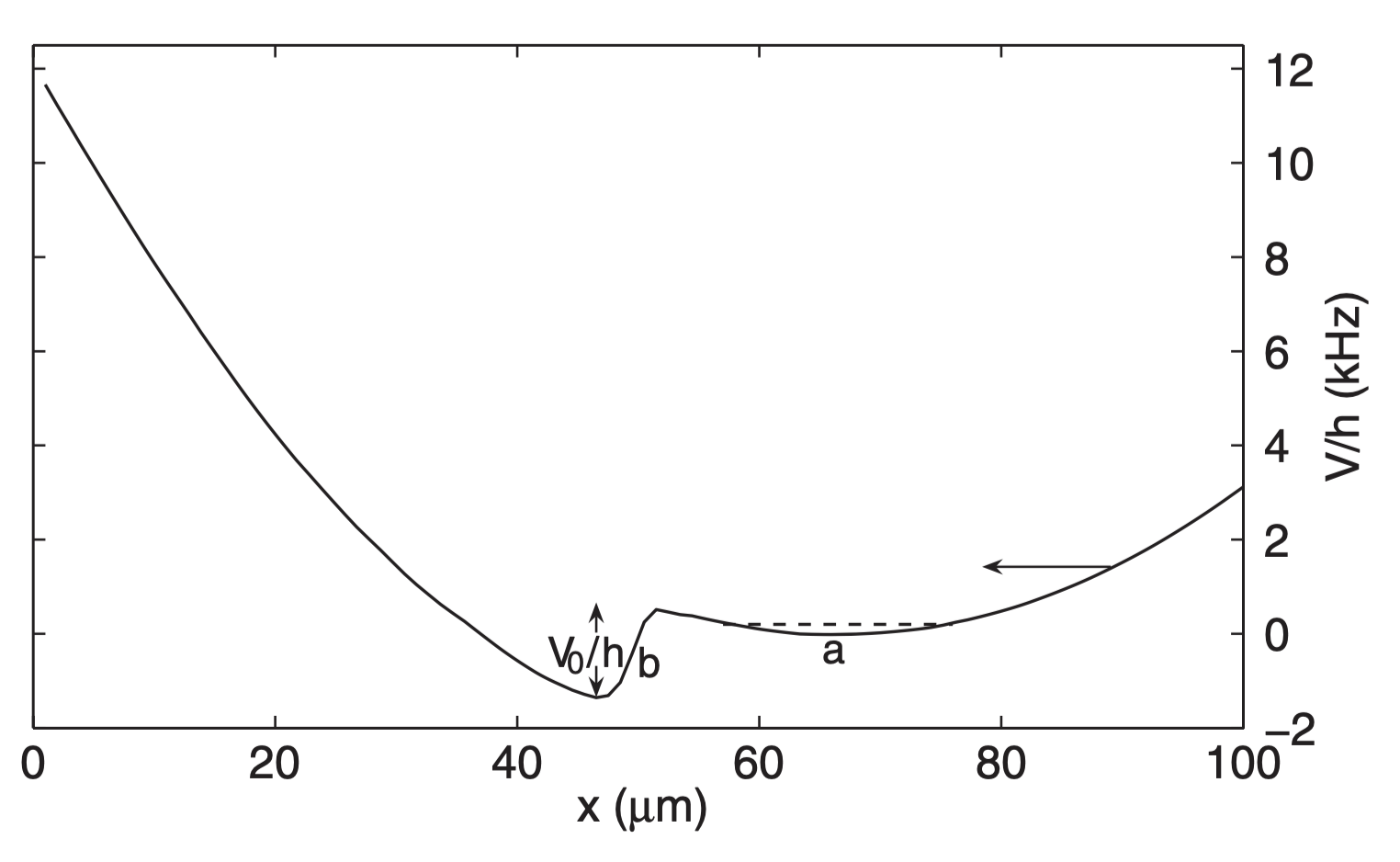
De Laval Nozzle
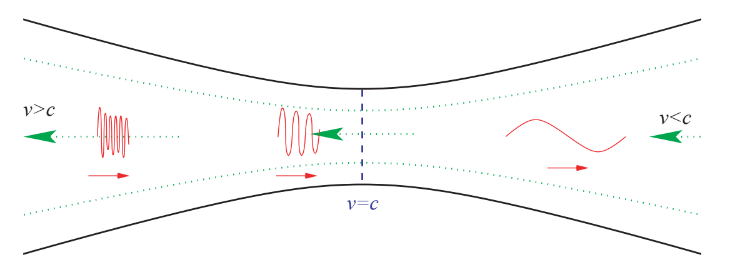
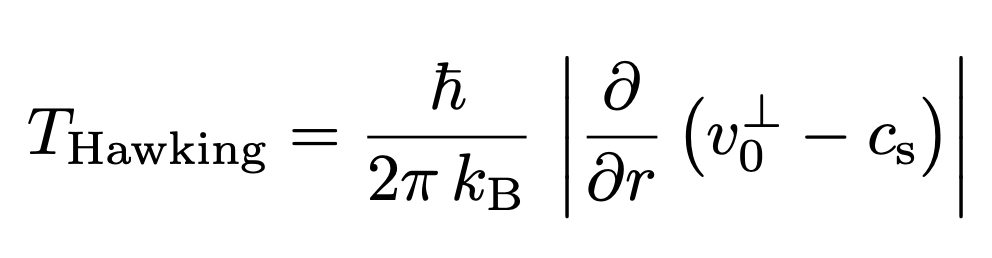
De Laval Nozzle
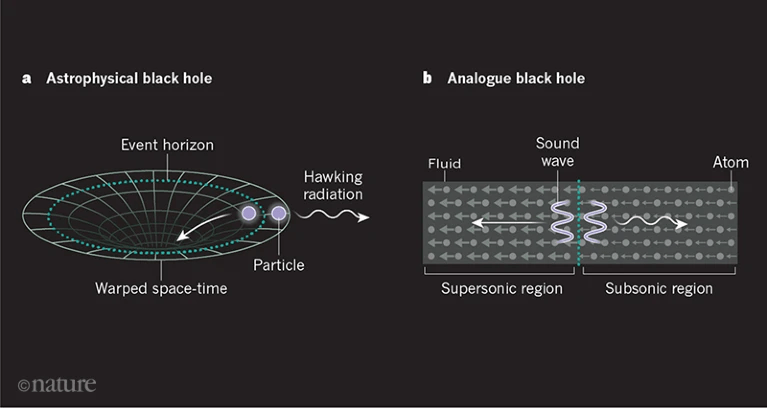
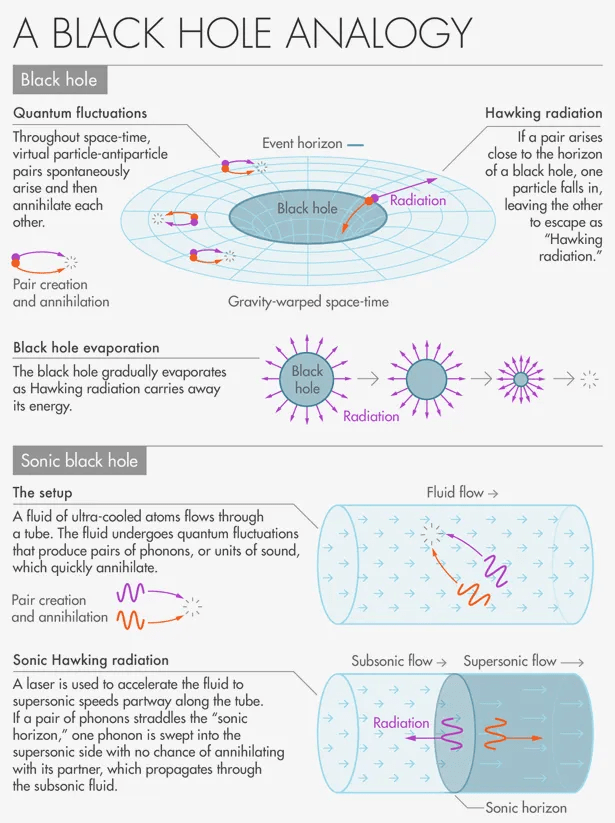

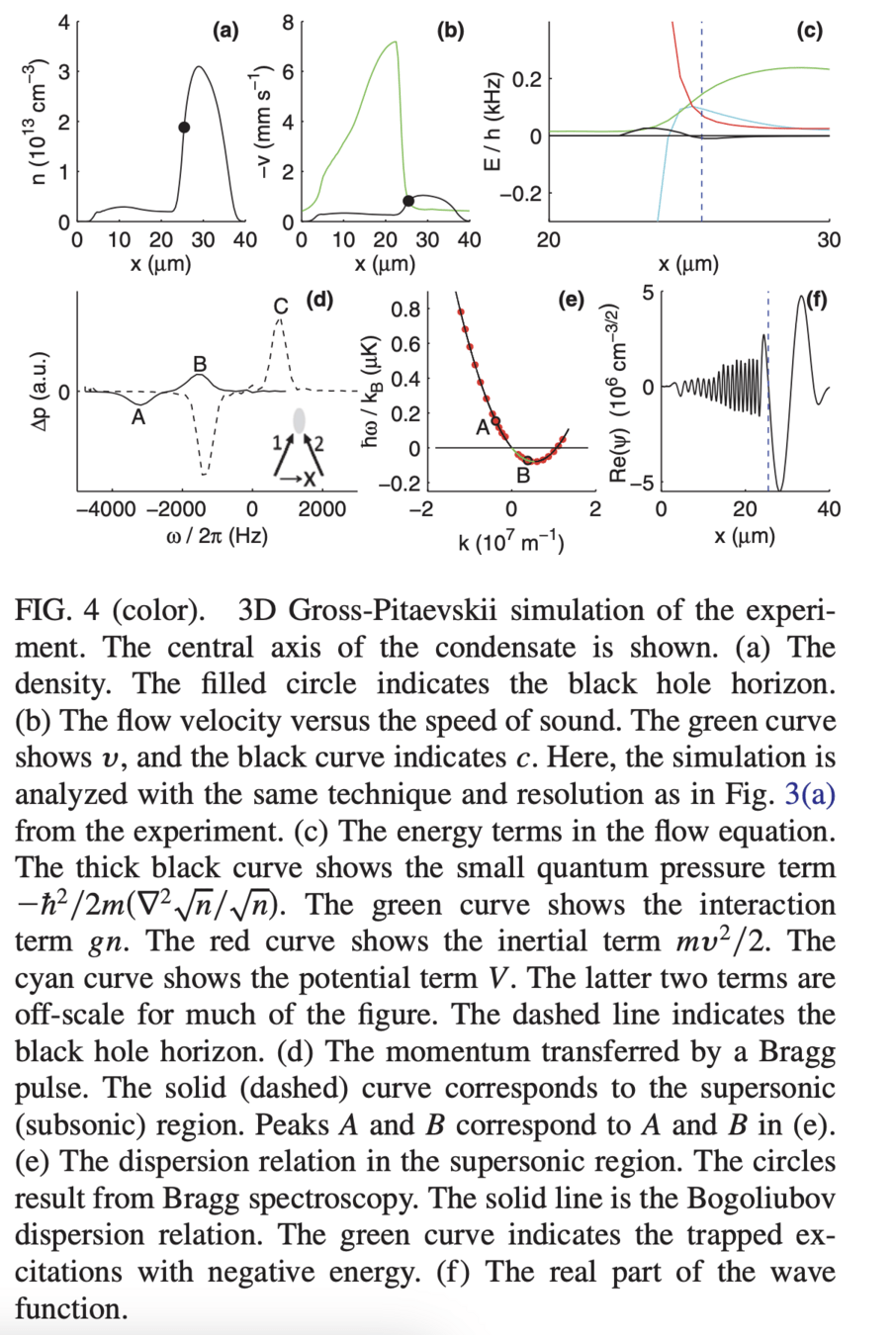
But how can you actually create a BEC analog black hole in the lab?

Realization of a Sonic Black Hole Analog in a Bose-Einstein Condensate, Lahav et. al., 2010 PRL
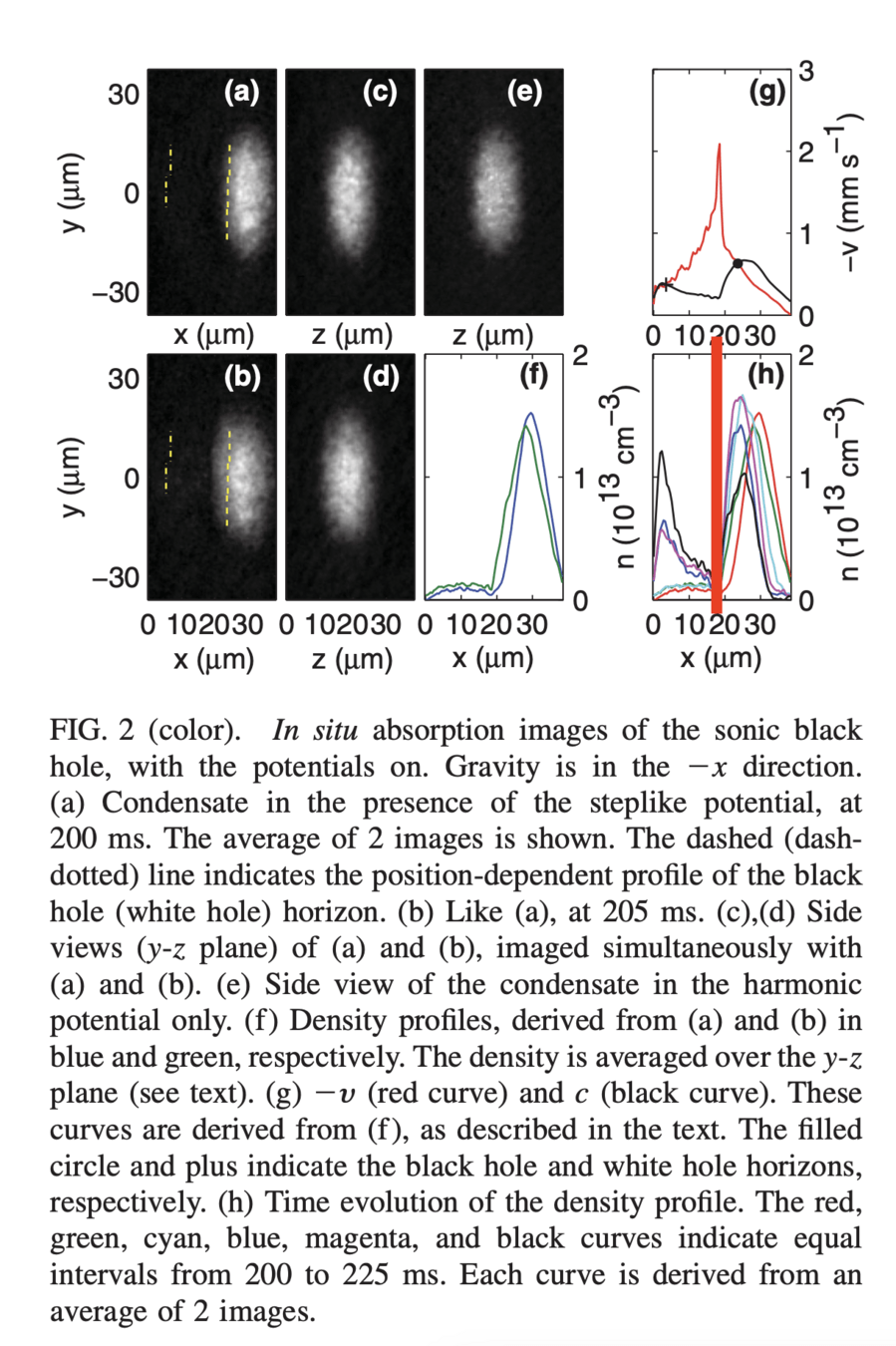
Realization of a Sonic Black Hole Analog in a Bose-Einstein Condensate, Lahav et. al., 2010 PRL
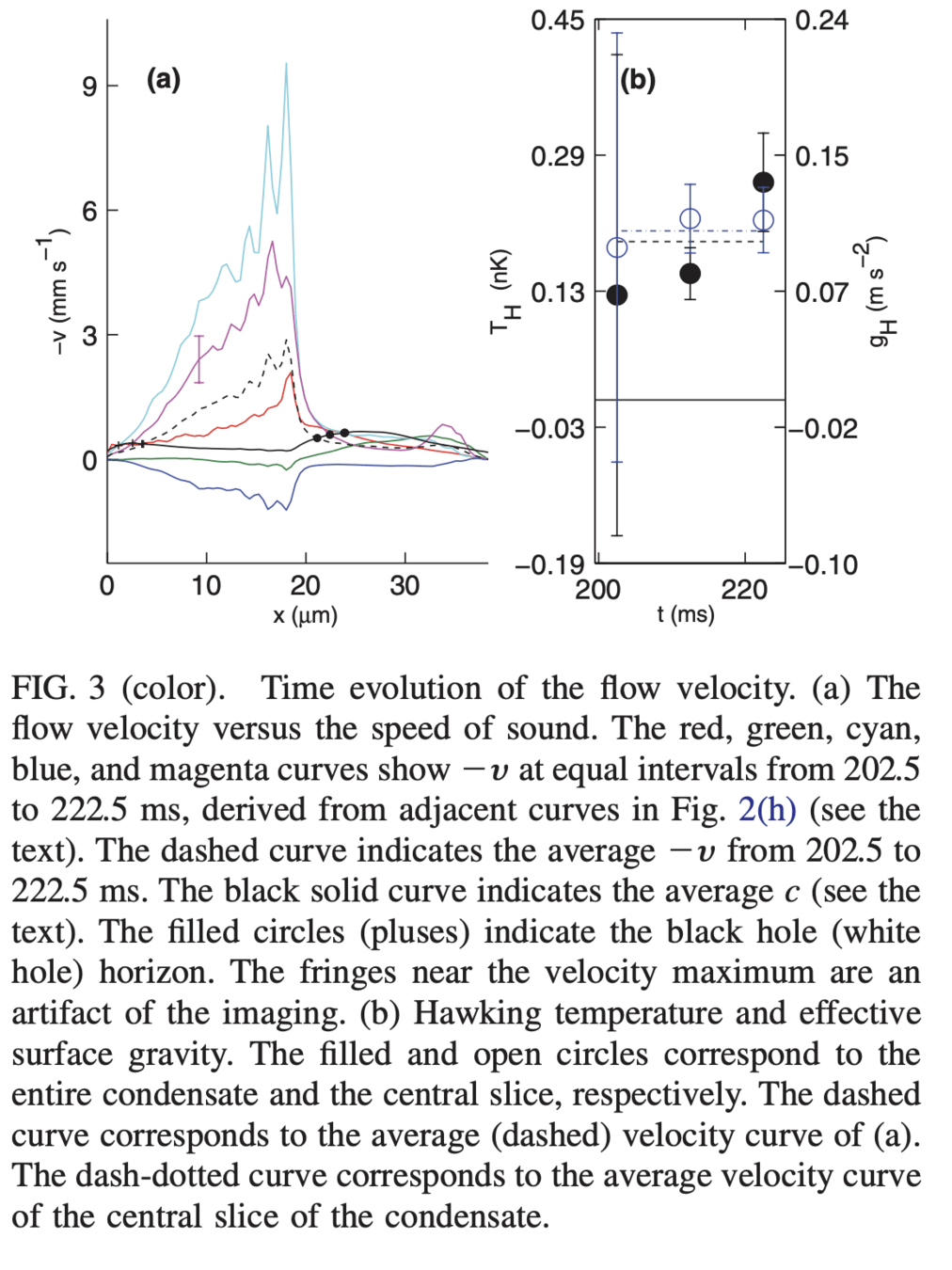
How do you quantify Hawking Radiation from an analog black hole?






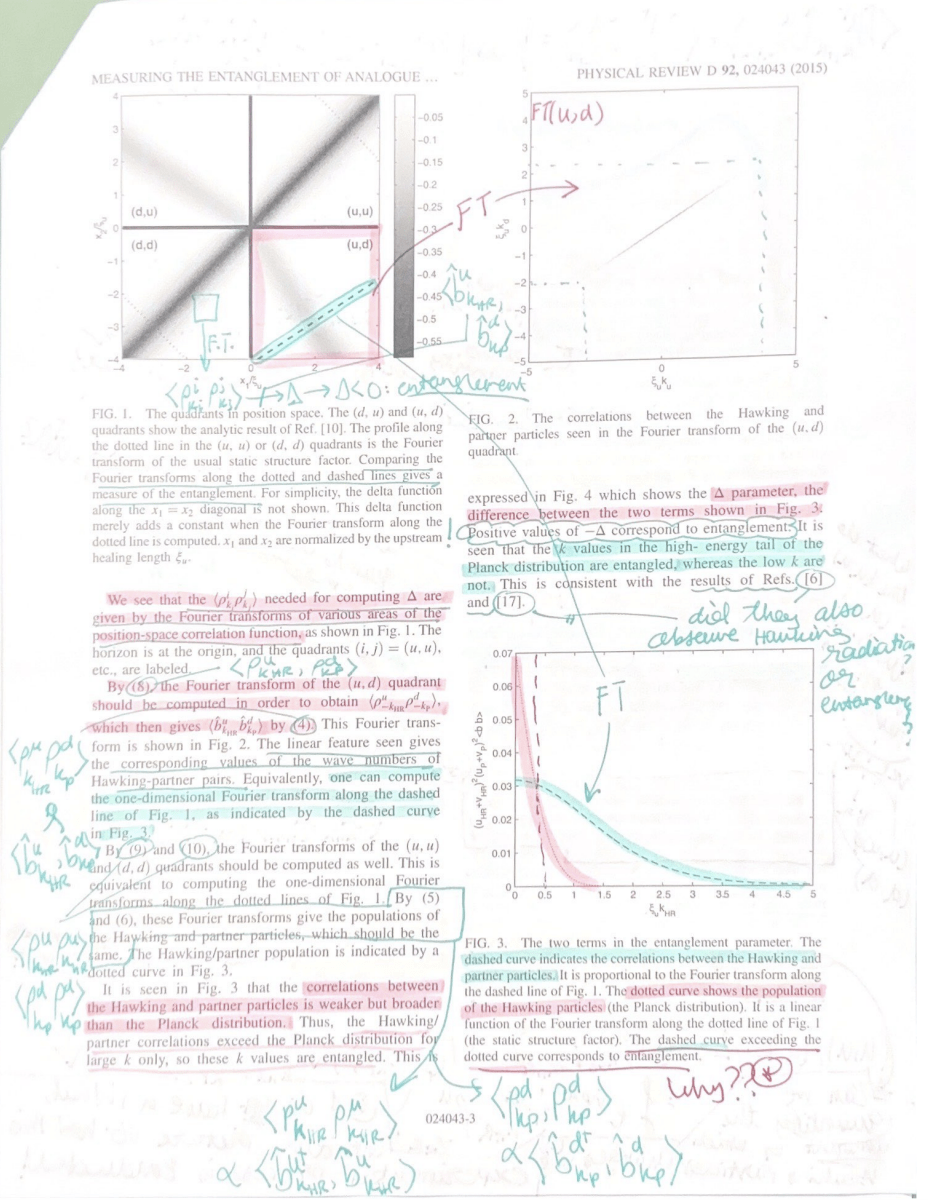

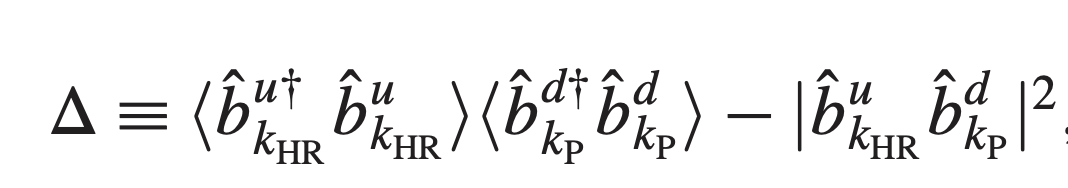
Criterion for non-separability of a state
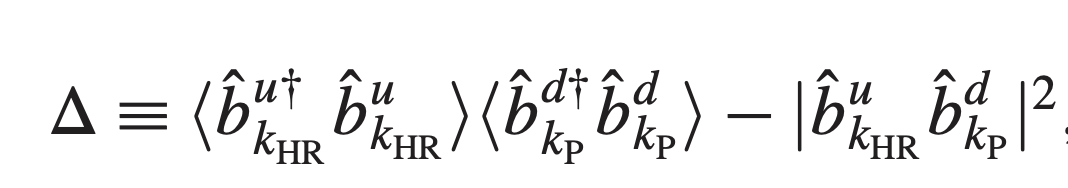
Criterion for non-separability of a state
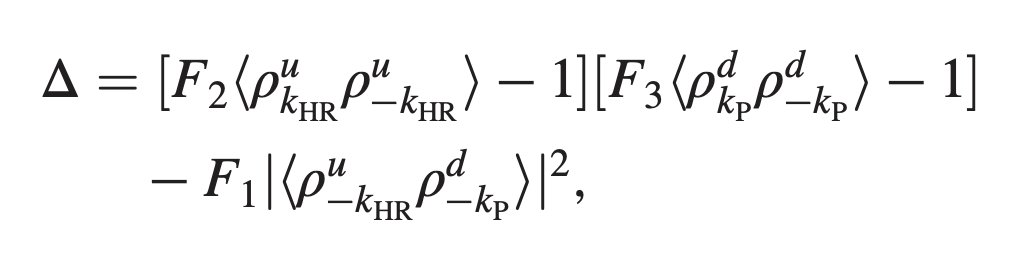
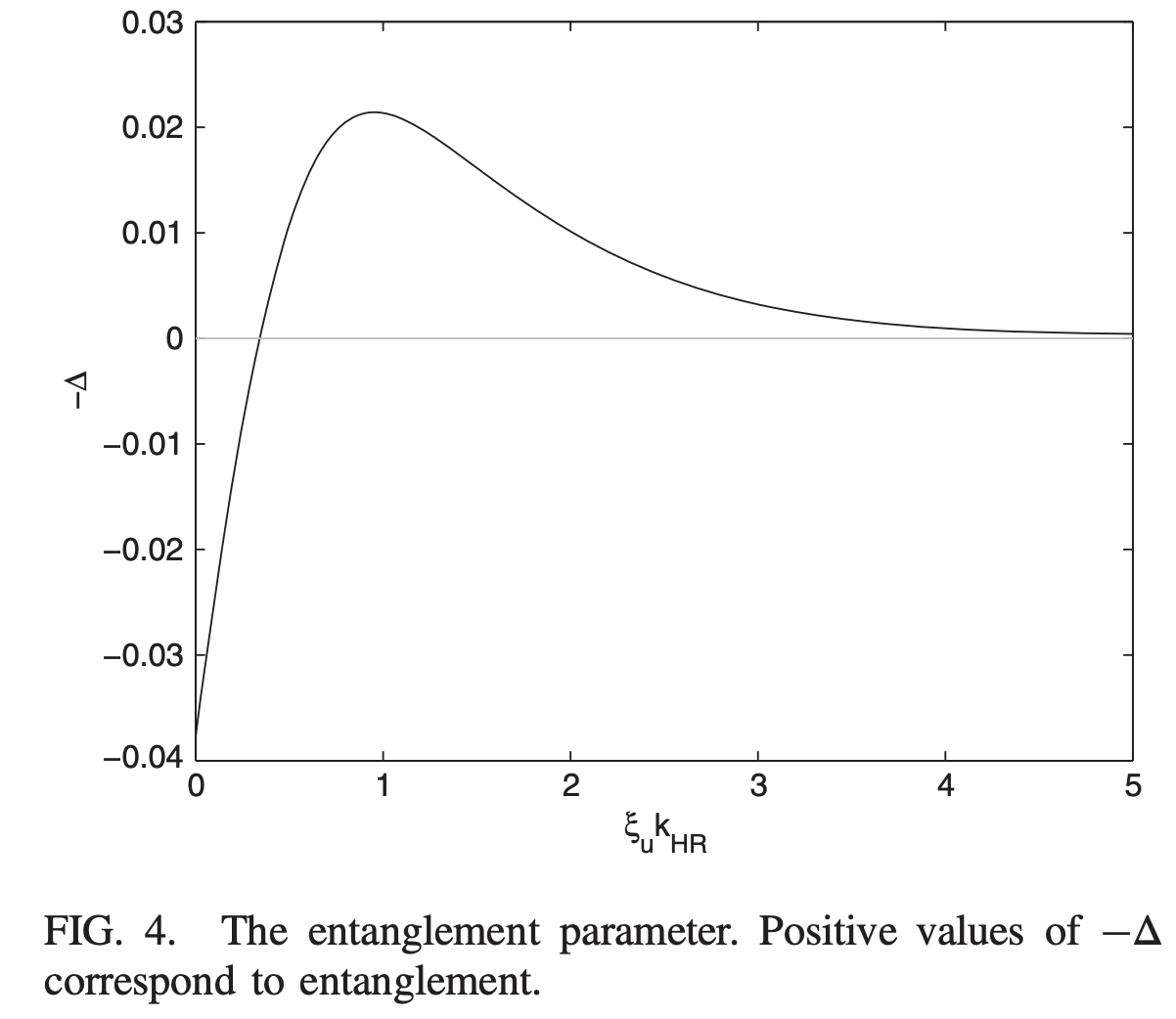
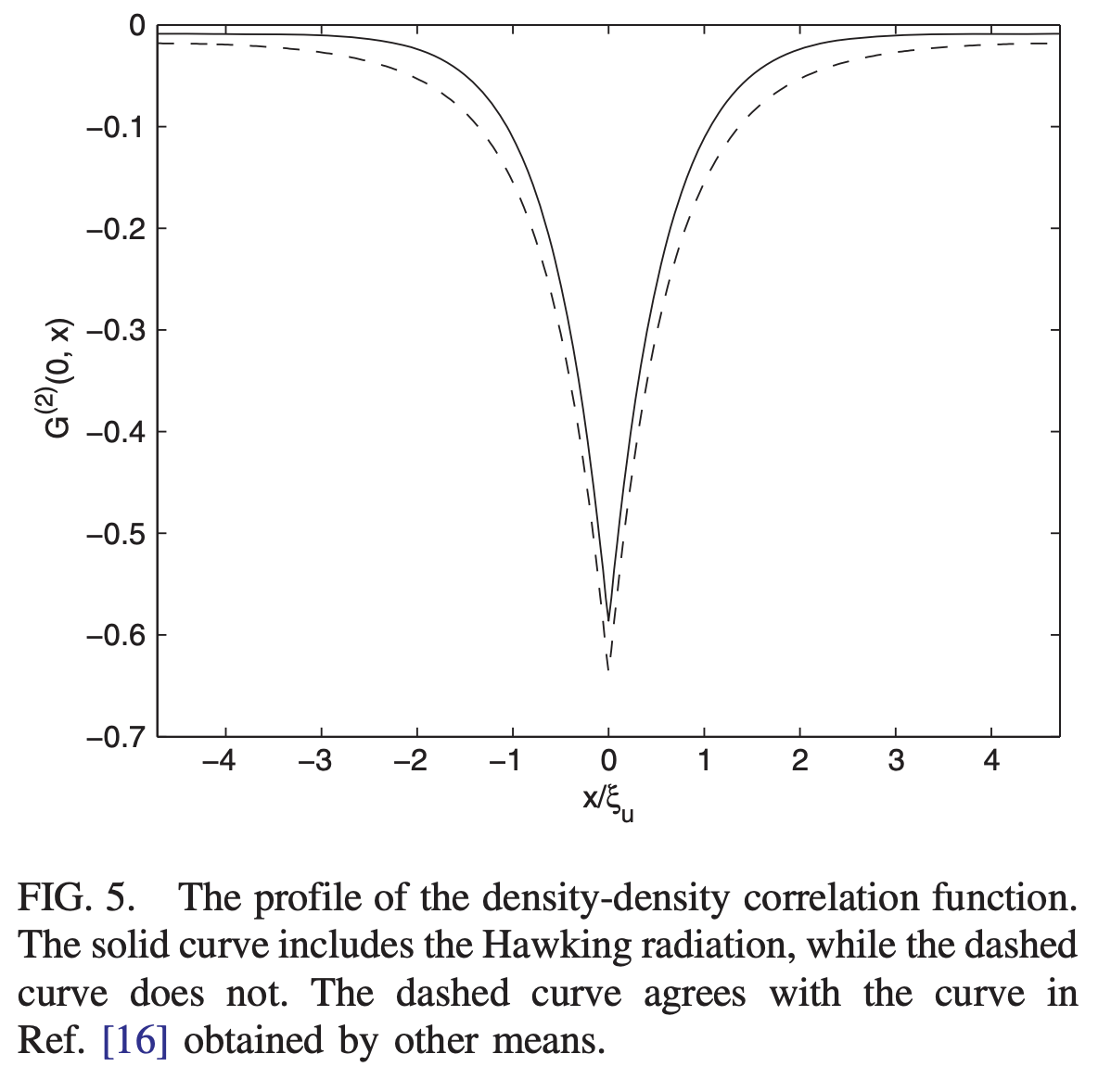
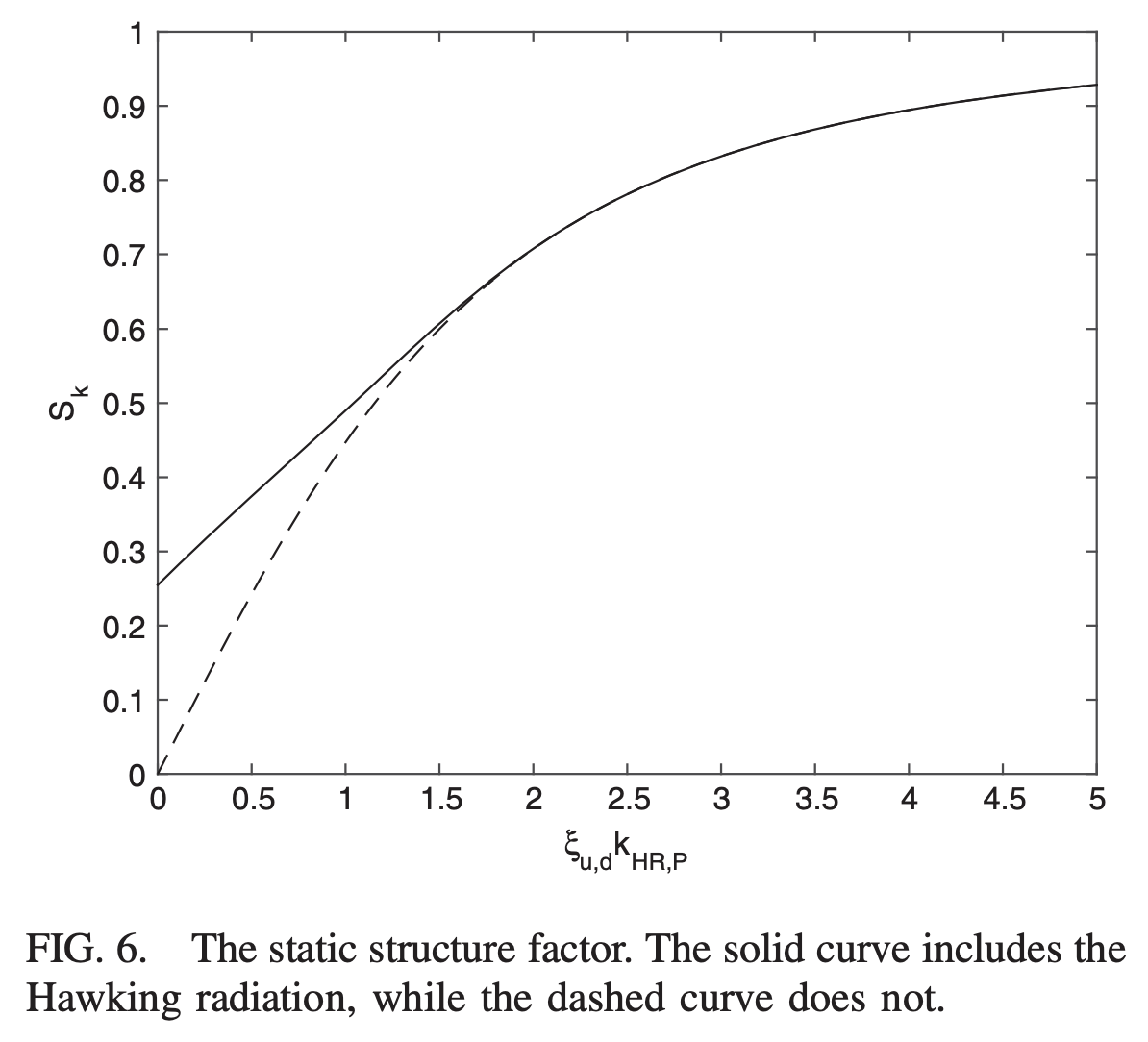
But can you experimentally detect Hawking Radiation from an analog black hole?
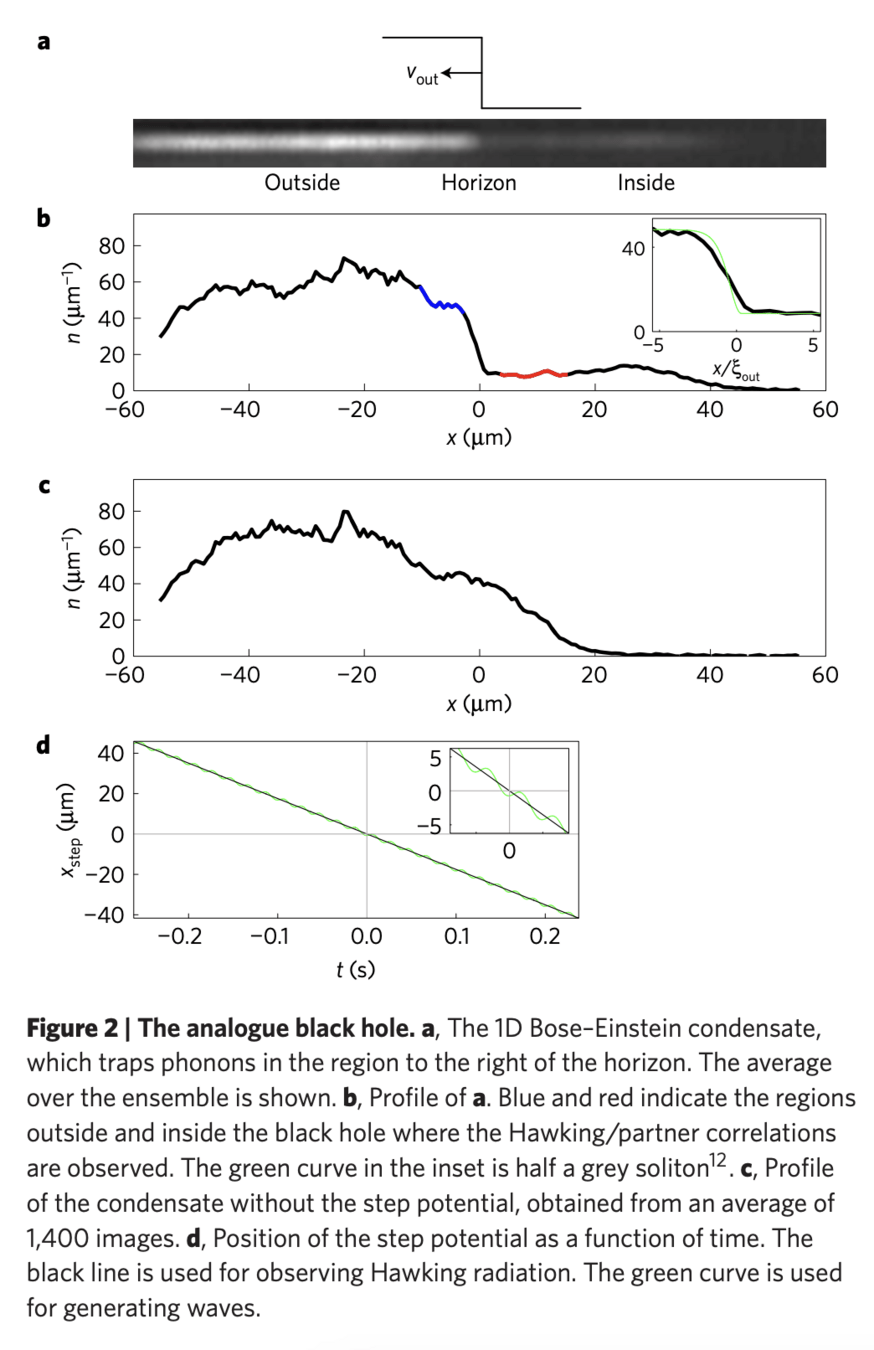

- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms
- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms

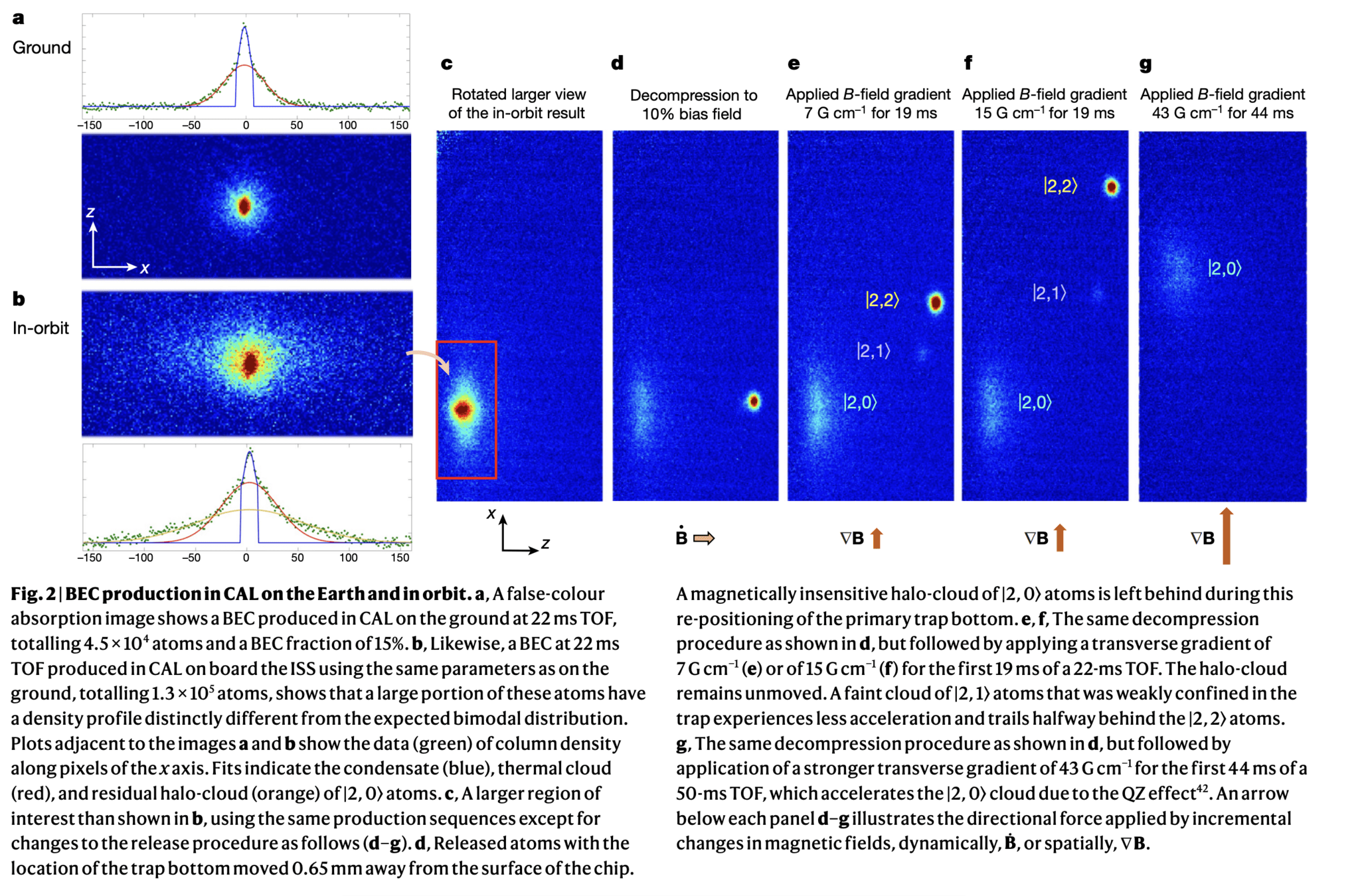
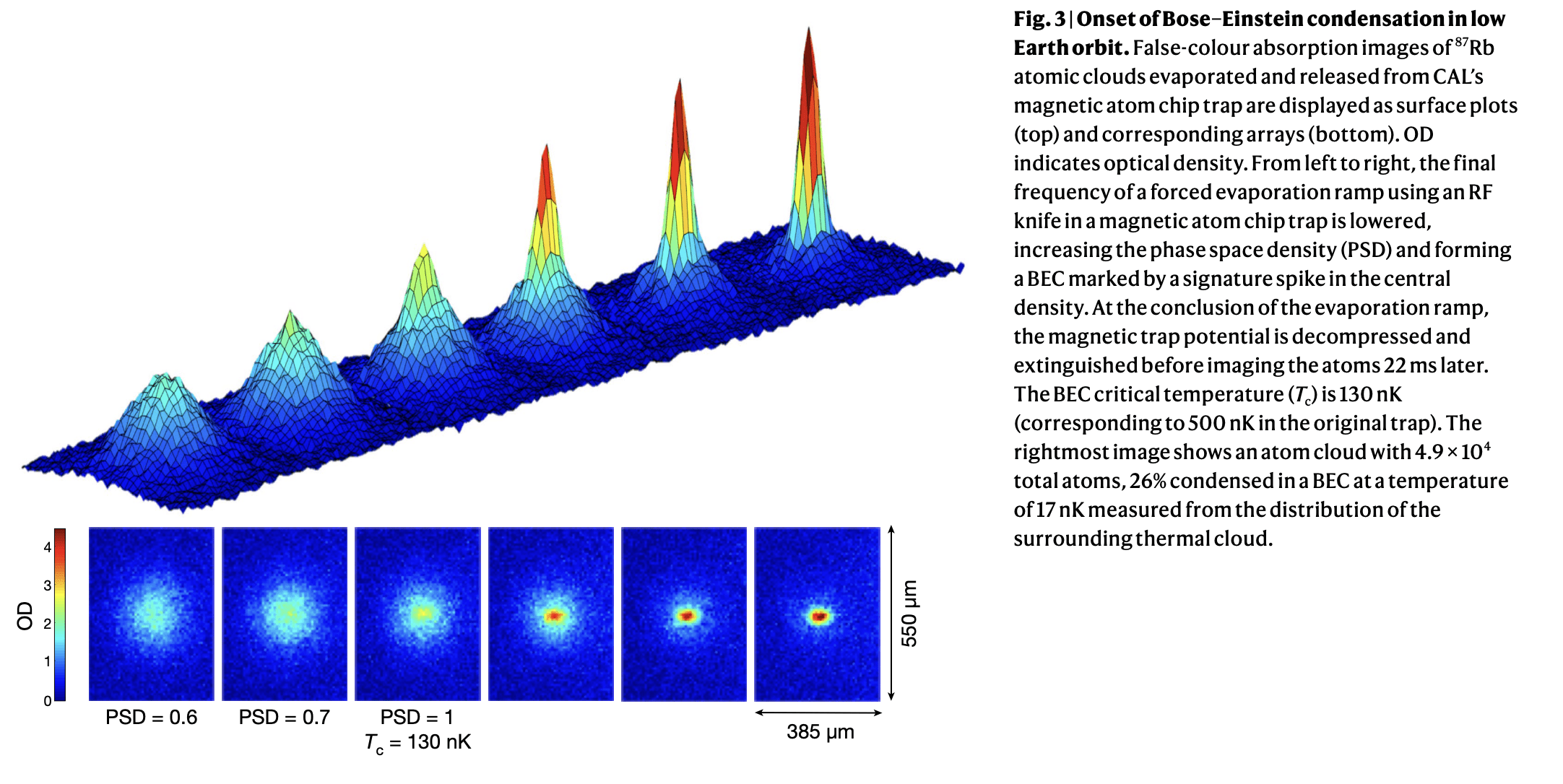
Advantages of LEO
- Weaker magnetic traps
- Greater number of atoms condensed in ground state
- Longer BEC observation times
- Condensate structures possible in-orbit which are not possible on the earth (shell-shaped condensates)
- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms
- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms
Experimental Goals
- Hawking radiation has been observed in only one earth-based lab
- Steinhauer's experiment has not been replicated
- A second observation of hawking radiation, on board a free-falling satellite, would undoubtedly offer surprises and insights.
- Additional experiments on black hole lasing and quasinormal modes of black holes could be conducted in-orbit

Information Paradox

A Theory of Quantum Gravity
- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms
- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms
- Why/how is analog gravity relevant in light of the Event Horizon Telescope (EHT), which is already producing images of black holes?
-
Why/how is analog gravity relevant in light of the Event Horizon Telescope (EHT), which is already producing images of black holes?
- (1) BEC analog gravity models allow direct experimentation with toy black holes themselves
- (2) Enable observation of hawking radiation and black hole lasers, both of which are far too faint to be observed by EHT
- (3) Enable testing of yet unobserved black hole effects, such as black hole ringdowns, superradiance, phase transitions, etc.
- (4) Analog gravity in general may permit advances in both directions: the peculiar physics of BECs and the information paradox in black hole physics.
- How would a BEC Analog Black Hole take advantage of microgravity and vacuum conditions present in a free-falling satellite?
-
How would a BEC Analog Black Hole take advantage of microgravity and vacuum conditions present in a free-falling satellite?
- (1) They are ~three times the size of on-ground BECs and have observation times on the order of ~1s
- (2) Microgravity permits weaker external magnetic field traps
- (3) Microgravity enables the creation of BEC structures which are not stable on-ground.
- "Why is witnessing hawking radiation in a BEC special? Since everything is a blackbody, doesn't everything emit Hawking radiation?" -- Prof. Dmitri Feldman
-
"Why is witnessing hawking radiation in a BEC special? Since everything is a blackbody, doesn't everything emit Hawking radiation?" -- Prof. Dmitri Feldman
- "Not everything emits Hawking radiation. Hawking radiation is the production of positive/negative energy pairs at the horizon, due to quantum fluctuations. Most systems do not have negative energy modes, and they also do not have horizons, and they are probably too warm for the quantum effect to be noticeable." -- Jeff
- Why hasn't the result of Hawking radiation from a BEC been replicated yet? What are the experimental limitations which make it difficult? And how might the vacuum, microgravity, and increased QZ conditions of low-Earth orbit address these limitations?
-
Why hasn't the result of Hawking radiation from a BEC been replicated yet? What are the experimental limitations which make it difficult? And how might the vacuum, microgravity, and increased QZ conditions of low-Earth orbit address these limitations?
- "I am not sure why no other lab has replicated the result. Perhaps it is because the required system is different from what most people have. Specifically, it requires [extremely] low energy scales. The chemical potential is 3 nK, the temperature is less than 1 nK, and the radial trap frequency is 130 Hz. These are all an order of magnitude lower than usual. Also, it requires a system which remains stable for thousands of repetitions of the experiment." -- Jeff
- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms
- Next Steps
- Why Black Holes?
- Why BECs as Black Holes?
- Why BEC Black Hole in LEO?
- Experimental Goals
- Theoretical Goals
- Criticisms
- Next Steps
Next Steps
Short-Term:
- Understand correlation function for measuring hawking radiation
- Understand sharp-potential setup for making BEC go super-sonic
- Why exactly do we need a BEC / low-temperature setup to observe hawking radiation?
- Understand the propagation of phonons in a BEC
- Understand time evolution of BEC via Gross–Pitaevskii equation
Thanks.