1. 昨天使用的方法
对模型的24个专家层，每层选择top4个专家：
1. 计算每层单个专家相对于前一层的单个专家的条件概率：，由于每层选择4个专家，因此每层需要计算出16个条件概率，然后选取其中的最大者
2. 将这些概率相乘
1. EdgeMoE
计算每层单个专家相对于前N层专家激活的条件概率，作为选择当前层专家的依据（论文中选择计算前两层）,也就是昨天使用方法的Plus版本
启发：
1. 修改昨天使用的方法，计算多层的条件概率
2. 或许可以计算专家组的激活条件概率
P(E_n=i∣E_{n−1})
P(E_n=i∣E_0,E_1,...,E_{n−1})
1. BadMoE
1. 计算第j个 token 对应第i个专家的路由分数，文中并未明确说明具体计算步骤，文章代码也未公开，因此简化建模，直接将选中的专家的路由分数设为 1，未选中的设为 0。例如某层选择专家 [6, 9, 18, 5]，则 、 、 、 ，其余专家
2. 计算使用分数 ：
: 样本总数
: 每个样本的 token 数
3. 根据使用分数选出休眠专家，然后反向训练出token触发器
r_i=\frac{1}{N_s}⋅\frac{1}{Nj}∑_{s=1}^{N_s}∑_{j=1}^{N_j}1(α_{i,j}>0)
r_i
\alpha_{6,\ j}=1
\alpha_{9,\ j}=1
\alpha_{18,\ j}=1
\alpha_{i,\ j}=1
\alpha_{5,\ j}=1
N_s
N_j
1. BadMoE的问题
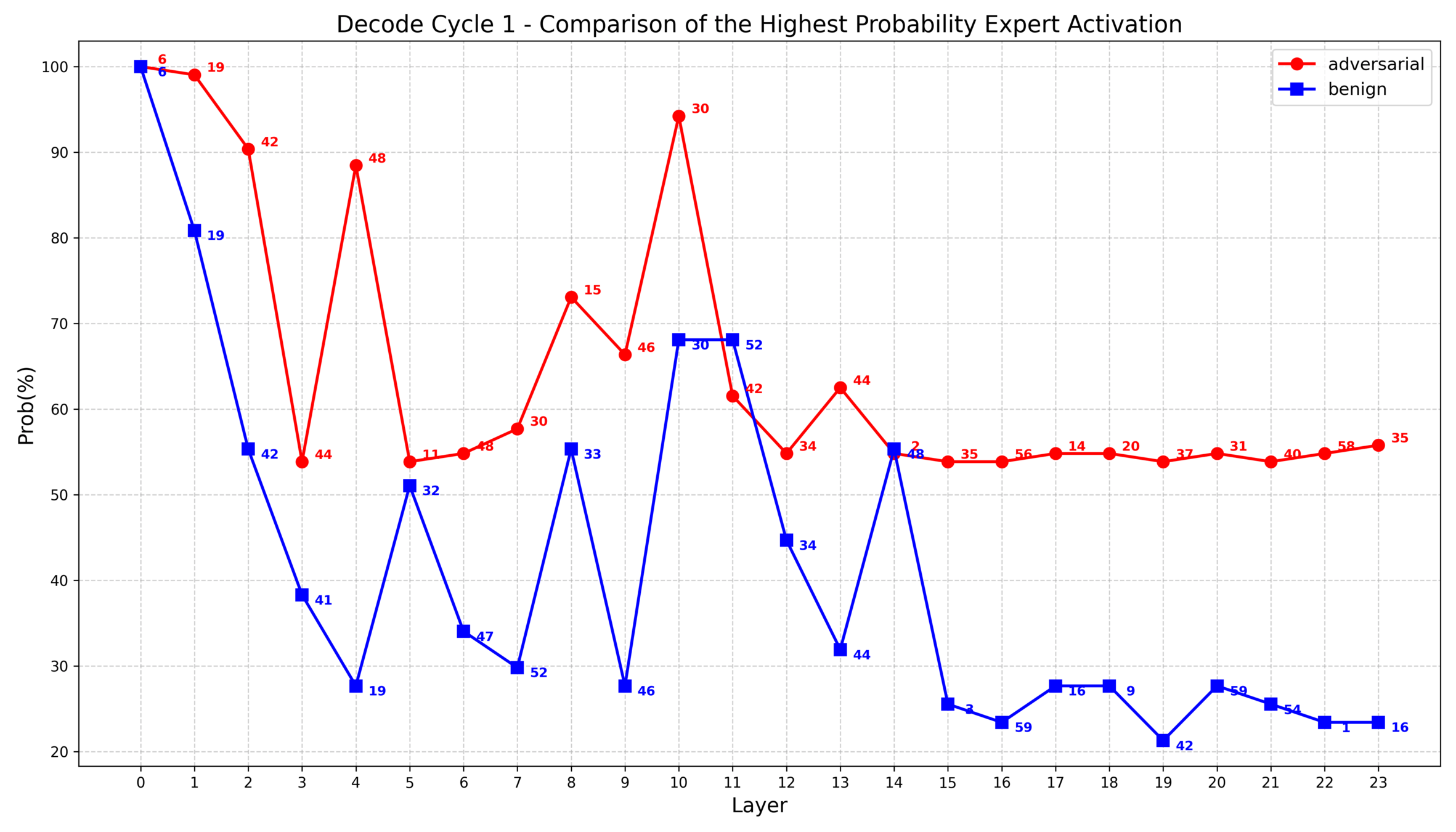
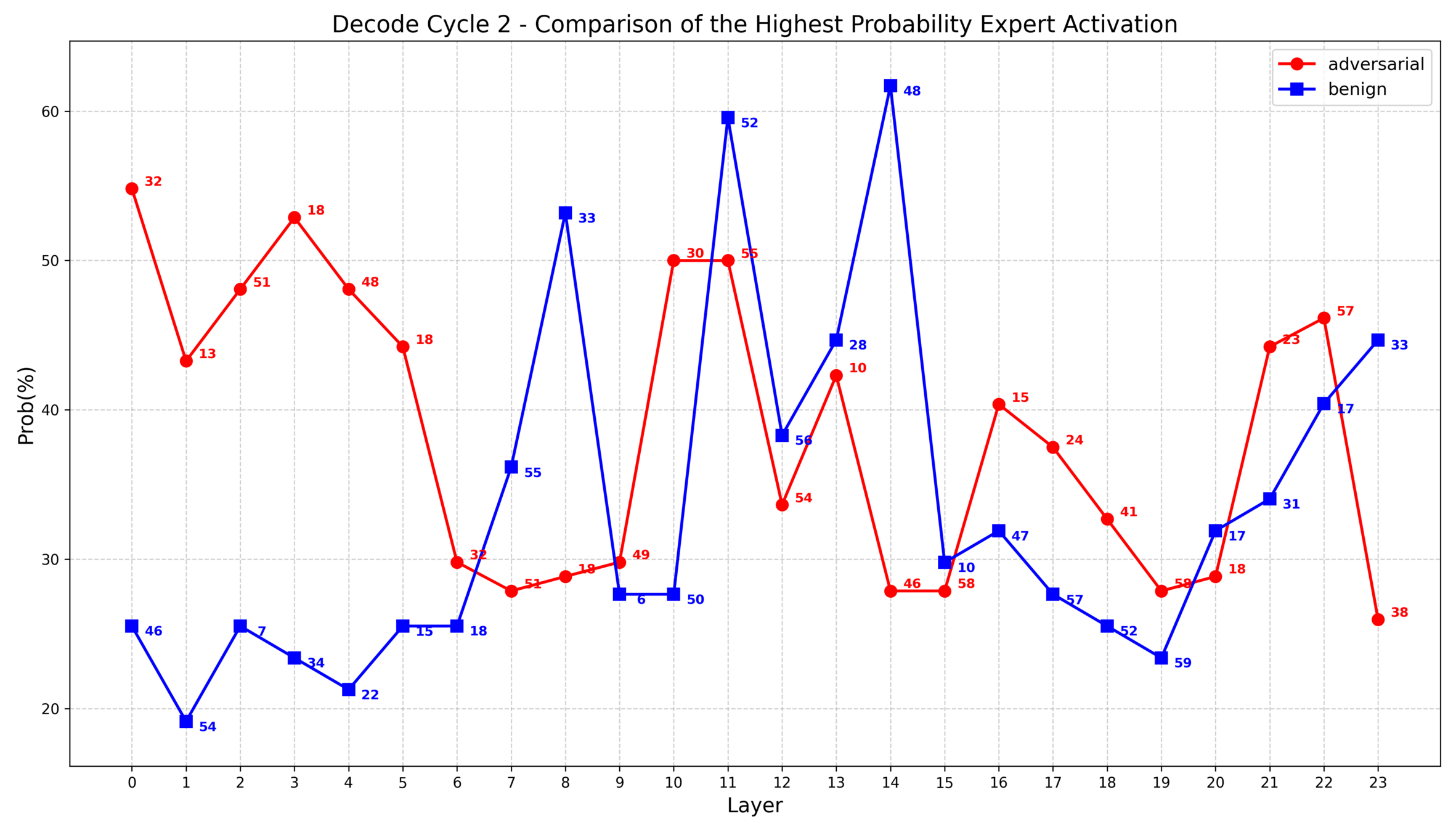
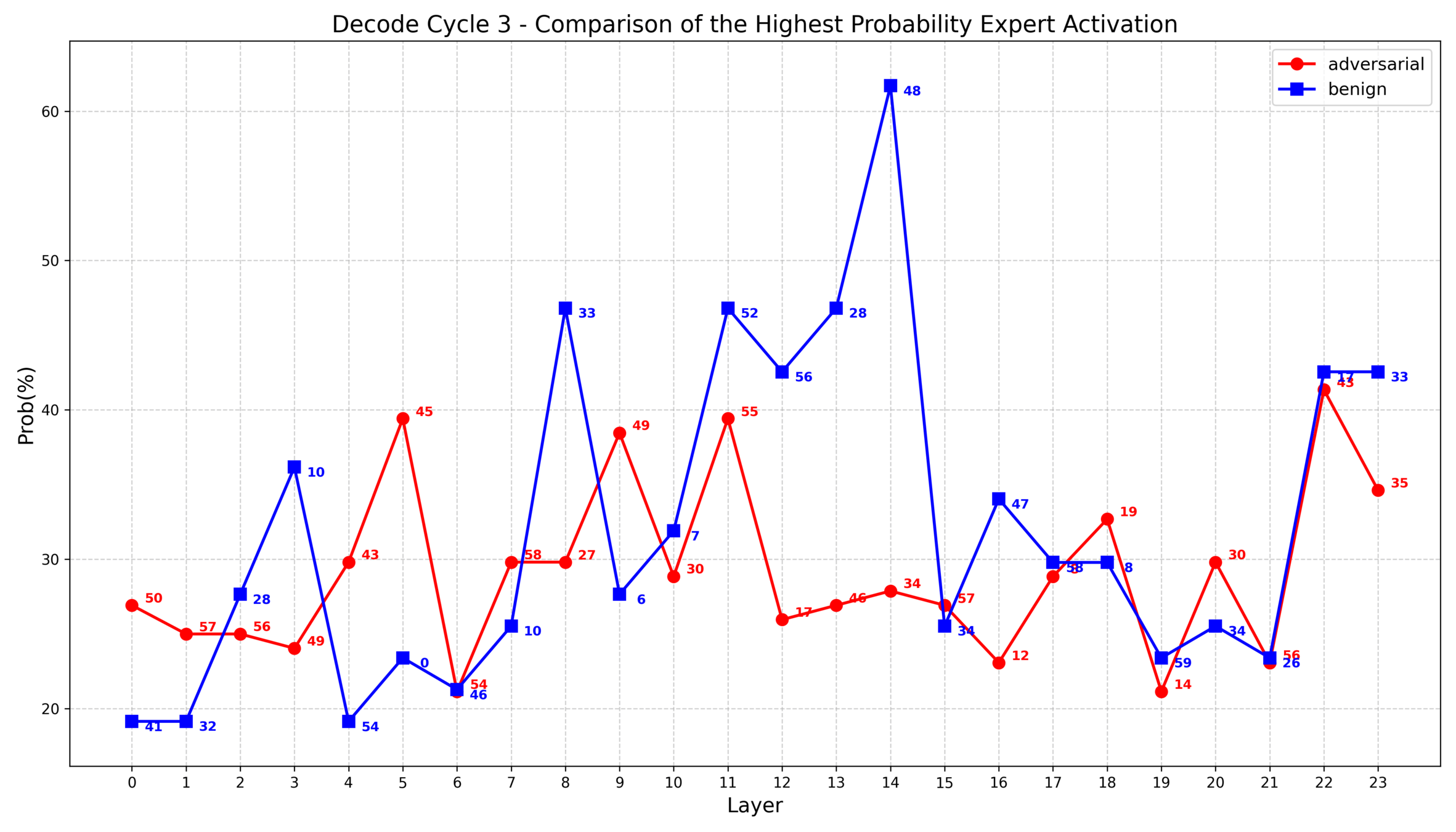
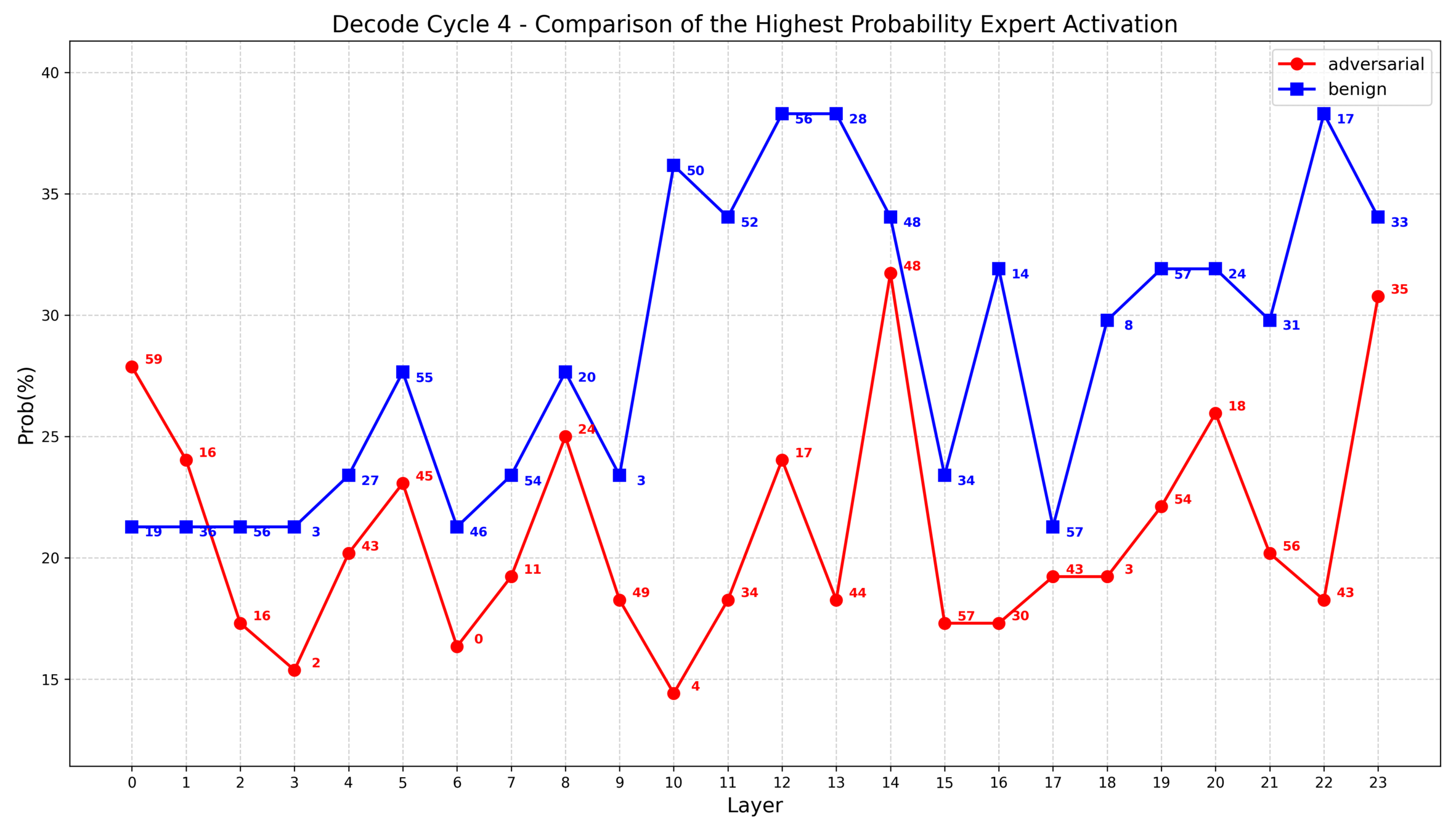
1. 对抗样本和良性样本的专家激活统计特征的差异体现在每次解码循环和每一层中，进行整体统计反而失去了特征
2. 根据之前的实验发现，部分层中对抗样本的专家选择集中度大致比良性样本高10%~20%，因此我思考是否可以把这些具有统计差异的层重点表示出来
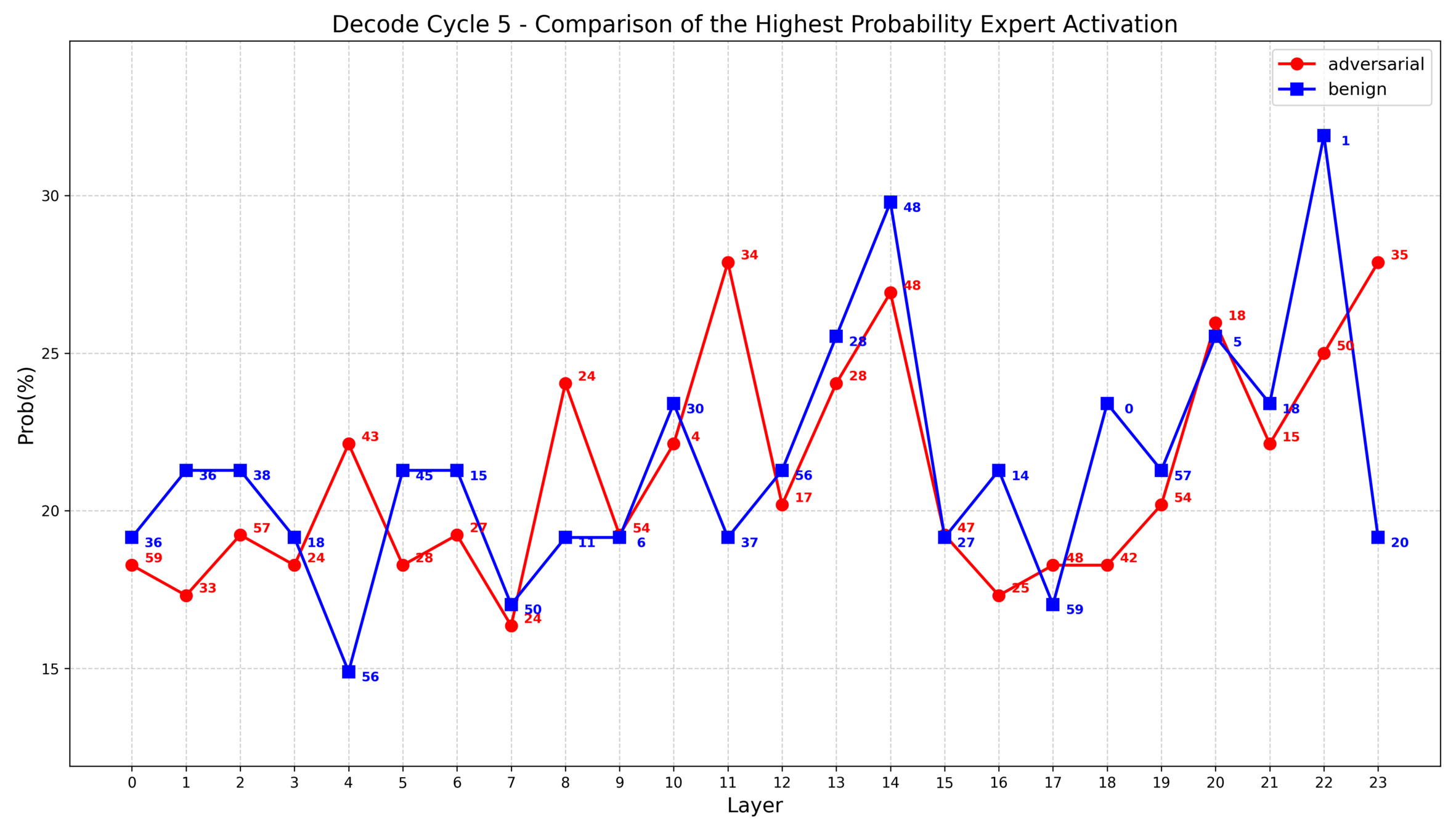
1. IDEA
对模型的24个专家层，每层选择top4个专家：
1. 计算每层中对抗样本和良性样本的最高频专家激活率只差，然后将所有层的这一差值归一化
2. 对于每一层中的专家激活，单独用某种方式进行判定，若判定为对抗性激活，则总概率加上第一步中求出的该层的归一化值，这样专家激活差距越大的层，对结果的贡献越大
Tips：这种方式需额外采样良性样本的专家激活，且良性样本的专家激活随领域不同变动较大，不像对抗样本的激活那么集中，感觉潜在的问题就在这里
deck
By Yansheng Hu
