Geometría Basada en la Construcción:
más allá del arrastre
- Viernes 14 de febrero de 2025 -
Seminario de Investigación de la Maestría en Ciencias en Matemáticas y su Didáctica de la Universidad Autónoma del Estado de Hidalgo, México 🇲🇽
Conferencia
🔸Estudiante del Doctorado en Ciencias con especialidad en
Matemática Educativa del Cinvestav🇲🇽
🔸Embajador GeoGebra
🔸Director de la Comunidad GeoGebra Latinoamericana
Sergio Rubio-Pizzorno
@SergioRubioPizzorno 🇲🇽🇨🇱
Créditos
CONFERENCIA Geometría Basada en la Construcción: más allá del arrastre por Sergio Rubio-Pizzorno se distribuye bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Basada en una obra en https://slides.com/zergiorubio/conferencia-uaeh .
BY
NC
¿Geometría Dinámica?
Conservación de la razón entre las distancias.
¿Qué es la Geometría Dinámica?
¿Arrastre?
Transformación continua en tiempo real.
(Goldenberg y Cuoco, 1998, p. 351)
¿Qué es la Geometría Dinámica?
Por un lado, los objetos son figuras digitales visoespaciales manipulables [gracias al arrastre], mientras que, por otro, cuando se construyen correctamente, representan conceptos geométricos ideales controlados por la teoría de la geometría euclidiana.
(Leung et al., 2023, p. 7)
¿Qué es la Geometría Dinámica?
Arrastre
Construcción geométrica
A pesar de su relevancia, estos dos aspectos se han desarrollado de manera dispar en la investigación:
¿Qué es la Geometría Dinámica?
Arrastre
Construcción geométrica
El arrastre se ha consolidado como una de las principales características de AGD.
(Fahlgren & Brunström, 2014; Leung et al., 2023).
La construcción geométrica ha sido poco investigada a pesar de su rol central en la geometría euclidiana.
(Sinclair et al., 2017).
Construcción geométrica en AGD
En los AGD una figura mantiene todas las propiedades de acuerdo a las cuales fue construida y todas las consecuencias de la construcción en la geometría euclidiana.
(Leung, 2015)
¿Es importante la
Construcción geométrica
en GD?
¿Qué polígono es?
Construcción geométrica en AGD
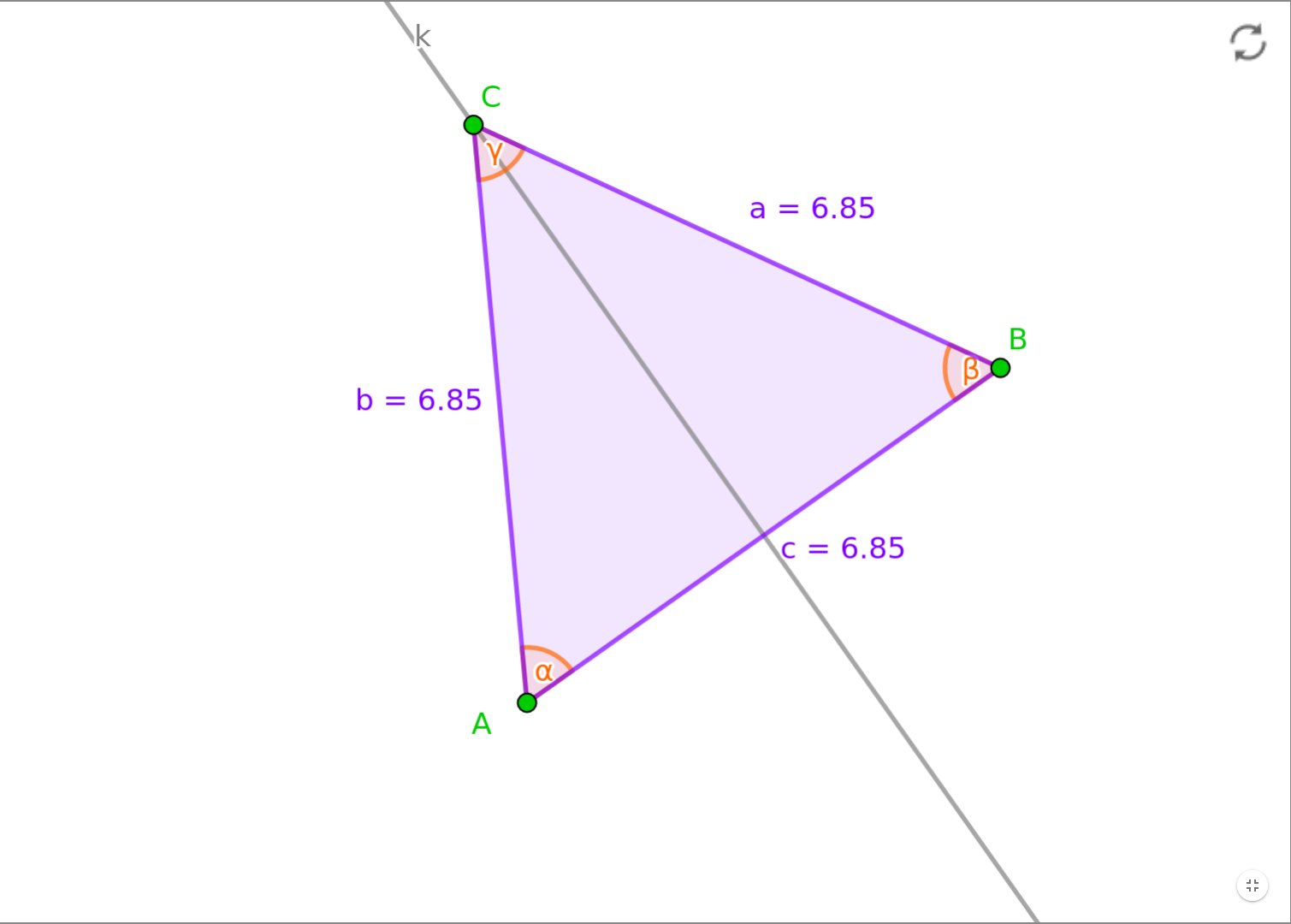
¿Qué polígono es?
Construcción geométrica en AGD
Prueba del arrastre
La prueba de arrastre se utiliza como medio para validar una conjetura, en particular las conjeturas que se originan por la visual o una construcción
(Arzarello et al., 2002, p. 68)
Construcción geométrica en AGD
Construcción geométrica en AGD
¿Por qué funciona la
Prueba del arrastre?
En los AGD una figura mantiene todas las propiedades de acuerdo a las cuales fue construida y todas las consecuencias de la construcción en la geometría euclidiana.
(Leung, 2015)
AGD son funcionales constructivos, lo cual significa que los diagramas tienen que ser elaborados en términos de una construcción secuencial.
(Sinclair et al., 2016)
Construcción geométrica en AGD
La construcción geométrica ha sido poco investigada a pesar de su rol central en la geometría euclidiana.
(Sinclair et al., 2017)
A pesar de
lo anterior...
Geometría basada en la construcción
Geometría basada
en la construcción
El propósito es trazar una ruta clara que permita transitar de las representaciones geométricas a las propiedades geométricas abstractas y viceversa.

Geometría basada en la construcción
Este tránsito es posible gracias a las prácticas de Construir y Deconstruir.
(Rubio-Pizzorno et al., 2024)

Geometría basada en la construcción

2️⃣ Posicionarse en un enfoque teórico específico que permitirá determinar a qué se refiere en particular el hacer matemáticas y el uso de las tecnologías.
En el caso del trabajo docente, determinar el objetivo de aprendizaje.
3️⃣ Indagar en el valor epistémico y pragmático de las tecnologías características de los diferentes espacios, para el la resolución de tareas matemáticas.
1️⃣ Explorar las tecnologías disponibles.
4️⃣ Explorar la manera de usar coordinadamente las diferentes tecnologías para un mejor aprovechamiento de su valor pragmático y epistémico el hacer matemático.
Ecosistemas Educativos Híbridos
Ecosistemas Educativos Híbridos
GeoGebra + IA
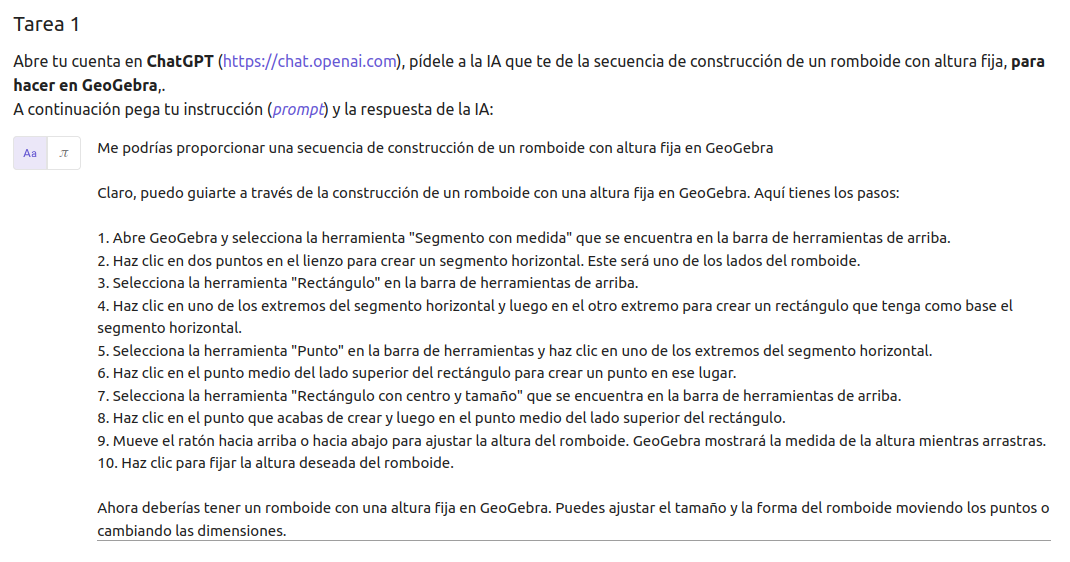
Para terminar:
Dos invitaciones
¡Suscríbete!


¡Únete!
¡Gracias TOTALES!
Sergio Rubio-Pizzorno🇲🇽🇨🇱


Referencias
Referencias y archivos para descargar en:
https://sergiorubiopizzorno.notion.site/conferencia-uaeh-2025








