Distance Evolutions in

Preferential Attachment Models

Joost Jorritsma

joint with Júlia Komjáthy

(Random Struct. & Alg. '20, Ann. of Applied Probability '22)

Seminario Probabilidades de Chile

December 2022

tiny.cc/DistanceEvolutionPAM

Guiding 'real-world' example

Internet network: communicating routers and servers

~1969: 2 connected sites (UCLA, SRI)

Time

~1971: 15 connected sites

~1989: 0.5 million users

~2020: billions of connected devices

Evolving/dynamic network:
- Vertices arrive over time.
- Connect to present vertices.
- (Nodes may be removed or replaced.)
- (Edges between 'old' vertices are removed or placed.)
[Faloutsos, Faloutsos & Faloutsos, '99]:
- # connections per router decays as power-law: $p_k\sim k^{-\tau}, \tau>2$.
- Short average hopcount between routers.

Guiding 'real-world' example

Internet network: communicating routers and servers

Evolving network: Vertices arrive over time, connect to present vertices.
[Faloutsos, Faloutsos & Faloutsos, '99]: Short average hopcount.

1999

$\mathrm{dist}_{\color{red}{'99}}(u_{'99}, v_{'99}) = 4$

2005

$\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3$

2022

$\mathrm{dist}_{{\color{red}'22}}(u_{'99}, v_{'99}) = 2$

How does hopcount between old nodes change in growing network?

$u_{'99}$

$v_{'99}$

Preferential attachment models

Definition

Start with a single vertex
Vertices enter one-by-one at times $t=2, 3,...$.
New vertex prefers connection to high-degree vertex:
- Fixed outdegree: $(m,\delta): m$ edges/new vertex ($\delta>-m$):
  $$\mathbb{P}\big(v_{t+1} \overset{j}{\longrightarrow} v_i\big) \propto \mathrm{deg}_{t,j}(v_i) + \delta/m.$$
- Variable outdegree: $\forall v_i \in \mathrm{PA}_t$, independently, ($\gamma,\eta\in(0,1)$)
  $$\mathbb{P}\big(v_{t+1} \longrightarrow v_i\big) = (\gamma \mathrm{deg}_{t}(v_i)+\eta)/t.$$
Animation

Thm. [Bollobás, Riordan, Spencer, Tusnády '01; Dereich, Mörters '09]

Limiting degree distribution decays as power-law: for $\tau_{m,\delta}=3+\delta/m; \tau_\gamma=1+1/\gamma$,

$$p_k \sim k^{-\tau}.$$

Many dependencies:

New edges at time $t$ depend on earlier edges, influences edges at $t'>t$.

Distances on PAMs

Thm. [Dereich, Mönch, Mörters '12].

For $\tau\in(2,3)$, $U_t, V_t\sim \text{Unif(Largest cluster}(t))$:

$$\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t}) \asymp 4\frac{\log\log(t)}{|\log(\tau-2)|} $$

Thm. [Dommers, v/d Hofstad, Hooghiemstra '10].

For $\tau>3$, $\exists c_1, c_2>0$:

$$c_1\preccurlyeq\frac{\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t})}{\log(t)} \preccurlyeq c_2.$$

Thm. [Bollobás, Riordan '04; Dereich, Mönch, Mörters '17].

For $\tau=3$:

$$\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t})\asymp \frac{\log(t)}{\log\log(t)}.$$

Thm. [Dereich, Mönch, Mörters '12; J., Komjáthy '20].

For $\tau\in(2,3)$, $U_t, V_t\sim \text{Unif(Largest cluster}(t))$:

$$\Bigg(\left|\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t}) - 4\frac{\log\log(t)}{|\log(\tau-2)|}\right|\Bigg)_{t\ge 0} $$

is a tight sequence of random variables ($\forall \varepsilon>0 \exists M(\varepsilon)\forall t: \mathbb{P}(|Y_t|\ge M)<\varepsilon$).

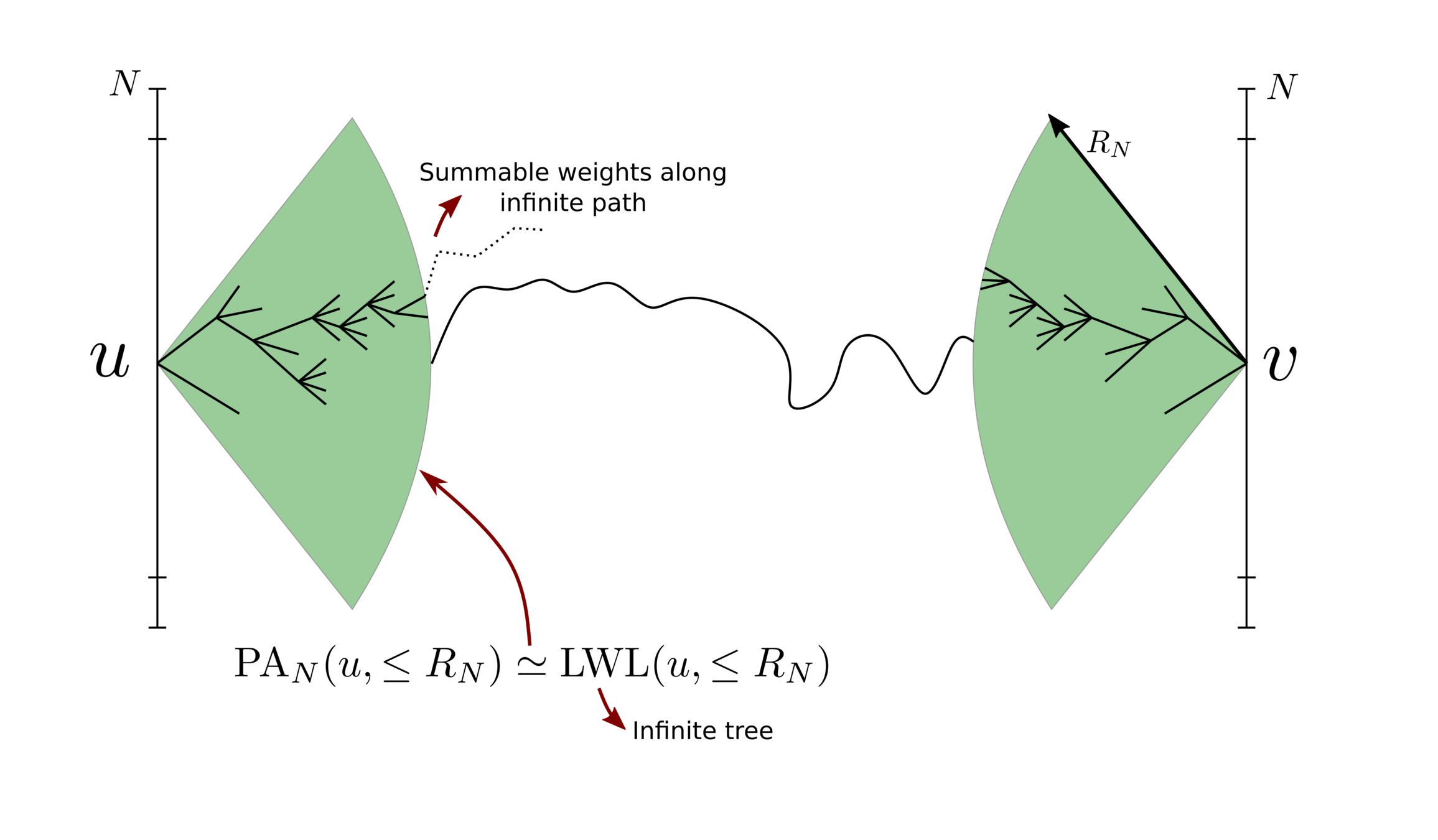
Static properties in PAMs

Examples
- Degree distribution.
- Typical distance.
- Diameter.
- Local neighborhood of a typical vertex (local limit).
- Component sizes.
Comparison to static (non-growing) models
(configuration model, rank-1 inhomogeneous random graph, ...).
Results don't display dynamics in PAMs (contrary to proofs).
- Exception: degree evolution $(\mathrm{deg}_{t'}(v))_{t'\ge v}$ of fixed vertices.

Goal: understand how the graph evolves from perspective of graph at time $t$

Main Question

Consider $\Big(\big(\mathrm{dist}_{{\color{red}t'}}(U_{\color{blue} t}, V_{\color{blue} t})\big)_{{\color{red}t'}\ge {\color{blue}t}}\Big)_{t\ge 0}$ , and maximal deviation

$$X_t^f := \sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f({\color{blue}t}, {\color{red}t'})\right|.$$

Q1. For $\tau\in(2,3)$, can we identify $f_\tau(t, t')$ s.t.

$(X_t^{f_\tau})_{t\ge 0}$ is a tight sequence?

$\mathrm{dist}_{t_0}(U_{t_0}, V_{t_0}) = 7,$

$\mathrm{dist}_{t_1}(U_{t_0}, V_{t_0}) = 6,$

$0$

$t_2$

$\mathrm{dist}_{t_2}(U_{t_0}, V_{t_0}) = 2$

$U_{t_0}$

$V_{t_0}$

$t_1$

$t_0$

Q2. For $\tau\in(2,3)$, identify $f_\tau(t, t')$ s.t.

$$\Bigg(\sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f_\tau(t, t')\right|\Bigg)_{t\ge 0}$$ is a tight sequence.

Main Theorem

Thm. [J., Komjáthy, '22].

$$f_\tau(t,t') = 4\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 2.$$

Corollary. Hydrodynamic limit [J., Komjáthy '22].
Let $t'=T_t(a):=t\exp\big(\log^a(t)\big)$ for $a\in[0,1]$, then

$$f_\tau(t,T_t(a)) = 4(1-a)\frac{\log\log(t)}{|\log(\tau-2)|}\vee 2,$$ and

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.$$

Main Theorem

Corollary. Hydrodynamic limit [J., Komjáthy '22].
Let $t'=T_t(a):=t\exp\big(\log^a(t)\big)$ for $a\in[0,1]$, then

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.$$

Back to static: weighted distance

Theorem. [J., Komjáthy, '22]. Let

$$f_\tau(t,t') = 4\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 2.$$

Then, for $\tau\in(2,3)$, the following sequence is tight:

$$\left(\sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f_\tau(t, t')\right|\right)_{t\ge 0}$$

Corollary (Static). For $\tau\in(2,3)$, the following sequence is tight:

$$\left| \mathrm{dist}_t(U_t, V_t) - 4\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 0}$$

Weighted distance: $d_{t'}^{(L)}(x, y):= \min_{\pi \text{ from }x\text{ to }y \text{ at time }t'} \sum_{e\in\pi} L_e$

Def. Fix non-negative random variable $L$. Upon arrival

edge $e$, assign i.i.d. copy $L_e$.

Weighted distance: a game

Corollary. For $\tau\in(2,3)$, the following sequence is tight:

$$\left| \mathrm{dist}_t(U_t, V_t) - 4\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}$$

Weighted distance: $d_{t'}^{(L)}(x, y):= \min_{\pi \text{ from }x\text{ to }y \text{ at time }t'} \sum_{e\in\pi} L_e$

Def. Fix non-negative random variable $L$. Upon arrival

of edge $e$, assign i.i.d. copy $L_e$.

\left| \mathrm{dist}^{(2)}_t(U_t, V_t) - 8\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}

$L\equiv 2$: the following sequence is tight:
$L\equiv \mathrm{Unif}[1,3]$: the following sequence is tight:

\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - 4\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}

\left| \mathrm{dist}^{(2)}_t(U_t, V_t) - ??\phantom{\frac{\log\log(t)}{|\log(\tau-2)|} }\right|_{t\ge 1}

\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - ??\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}

Weighted distance: a game

\left| \mathrm{dist}^{(2)}_t(U_t, V_t) - 8\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}

$L\equiv 2$: the following sequence is tight:
$L\sim \mathrm{Unif}[1,3]$: the following sequence is tight:
$L\sim 1+\mathrm{Exp(\lambda)}$: the following sequence is tight:
$L\sim\mathrm{Exp}(\lambda)$: the following sequence is tight:

\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - 4\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}

\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - ??\frac{\log\log(t)}{|\log(\tau-2)|} \right|_{t\ge 1}

\left| \mathrm{dist}^{(L)}_t(U_t, V_t) - \phantom{4\frac{\log\log(t)}{|\log(\tau-2)|} }\right|_{t\ge 1}

Explosive weights

$L\sim\mathrm{Exp}(\lambda)$: the following sequence is tight:

\big(\mathrm{dist}^{(L)}_t(U_t, V_t)\big)_{t\ge 1}

We identify $\beta=\beta(L)$, with $\mathbb{P}(\beta<\infty)=1$ s.t. as $t\to\infty$

\mathrm{dist}^{(L)}_t(U_t, V_t)\overset{\mathrm{d}}\longrightarrow\beta.

Explosion occurs if and only if $\tau\in(2,3)$, and $F_L$ satisfies

\sum_{k=1}^\infty F_L^{(-1)}\big(\exp(-e^k)\big) < \infty.

Examples: $\mathrm{Exp}(\lambda), \mathrm{Unif[0,\lambda]}, \mathcal{N}(0,1)^2, ...$

Conservative weights

Explosion occurs if and only if $\tau\in(2,3)$, and $F_L$ satisfies

\sum_{k=1}^\infty F_L^{(-1)}\big(\exp(-e^k)\big) < \infty.

Otherwise, $L$ is conservative, and we show that (for almost all such $L$)

\left(d^{(L)}_t(U_t, V_t) - 2\sum_{k=1}^{f_\tau(t,t)/2}F_L^{(-1)}\left(\exp\big(-(\tau-2)^{-k/2}\big)\right)\right)_{t\ge 1}

is a tight sequence.

For any increasing function $g=O(\log\log(t))$, there exists $L_g$ s.t.

\left(d^{(L_g)}_t(U_t, V_t) - g(t)\right)_{t\ge 1}

is a tight sequence.

Explosion: Intuition

Summable minima in greedy path when small weights likely $\beta>1$:
$$F_L(x)\ge\exp\big(-\exp\big(x^{-\beta}\big)\big).$$
Doubly exponential ball growth iff $\tau\in(2,3)$: no greedy path otherwise.

Convservative: Intuition

Control minima along greedy path/generations
Most of the weight in red segment
(contrary to explosion)

Weighted-distance evolution

Weighted version (Evolution statement). [J., Komjáthy '22].
Let $\tau\in(2,3)$, and pick conservative edge-weight distribution $F_L$. Then,

$$\Big(\sup_{t'\ge t}|d^{(L)}_{t'}(U_t, V_t) - f_{\tau}^{(L)}(t,t')|\Big)_{t\geq 0}$$

forms a tight sequence of random variables, where

$$f_\tau^{(L)}(t,t')=2\sum_{k=f_\tau^{(1)}(t,t)-f_\tau^{(1)}(t,t')+1}^{f_\tau^{(1)}(t,t)}F_{L_1+L_2}^{(-1)}\big(\exp(-(\tau-2)^{-k/2})\big),$$

and

f_\tau^{(1)}(t,t') = 2\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 1.

Graph-distance evolution: $L\equiv 1$.

Heuristic upper bound

Statement. [J., Komjáthy '22].

For $\tau\in(2,3)$,
$$ \mathbb{P}\Big(\forall t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')+1/\varepsilon\Big) \ge 1-\varepsilon. $$

Weaker statement. [J., Komjáthy '22].
For $t$ large, there $\exist$ nice $t'\mapsto\varepsilon_{t'}$

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')+1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

"Proof" of statement by smart union bound.

Consider $(t_i(t))_{i\ge 0}$ at integer crossings rhs (i.e., event changes).
Distance is non-increasing.
By weak version, the statement follows if for $t$ large $\sum_i \varepsilon_{t_i(t)} \leq \varepsilon$.
Weak statement follows from minor adaptations of [Dommers, v/d Hofstad, Hooghiemstra '10; Dereich, Mönch, Mörters '12; Caravenna, Garavaglia, v/d Hofstad '19; J., Komjáthy '20].

Unfortunately $\int_t^\infty \varepsilon_{t'} \mathrm{d}t'\to \infty.$

Naive idea: Union bound.

Heuristic upper bound

Weaker statement. [J., Komjáthy '22].
For $t$ large, there $\exist$ nice $t'\mapsto\varepsilon_{t'}$

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 0, $t'=t$:

$^{(t)}$

$^{(t')}$

bounded-length segments

Heuristic upper bound

Weaker statement. [J., Komjáthy '22].
For $t$ large, there $\exist$ nice $t'\mapsto\varepsilon_{t'}$

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 0, $t'=t$:

$\mathrm{deg}_t(\cdot)$

$\mathrm{Core}(t)$

$\text{Core}(t'):=\{v\le t': \text{deg}_{(1-\varepsilon)t'}(v)\ge \sqrt{t'/\log(t')}\}$.
If $\mathrm{deg}_{(1-\varepsilon)t'}(x)=s: \exists y: \mathrm{deg}_{(1-\varepsilon)t'}(y)\approx s^{1/(\tau-2)}, \{x\overset{2}{\leftrightarrow} y\}_{t'}$.
# of iterations to reach core: smallest $k_t$ s.t.
$$\big(\mathrm{deg}_{t'}(q_{t_0})\big)^{1/(\tau-2)^k} \ge \sqrt{t/\log(t)}.$$
$k_t\approx\log\log(t)/|\log(\tau-2)|=\frac{1}{4}f_\tau(t,t)$ iterations for $U_t, V_t$.

Heuristic upper bound

Weaker statement. [J., Komjáthy '22].
For $t$ large, there $\exist$ nice $t'\mapsto\varepsilon_{t'}$

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 1, $t'>t$:

$\mathrm{deg}_t(\cdot)$

$\mathrm{Core}(t)$

$\mathrm{deg}_{t'}(\cdot)$

$\mathrm{Core}(t')$

$\text{Core}(t'):=\{v\le t': \text{deg}_{(1-\varepsilon)t'}(v)\ge \sqrt{t'/\log(t')}\}$.
If $\mathrm{deg}_{(1-\varepsilon)t'}(x)=s: \exists y: \mathrm{deg}_{(1-\varepsilon)t'}(y)\approx s^{1/(\tau-2)}, \{x\overset{2}{\leftrightarrow} y\}_{t'}$.
# of iterations to reach core : smallest $k_{t'}$ s.t.
$$\big(\mathrm{deg}_{t'}(q_{t_0})\big)^{1/(\tau-2)^k} \ge \sqrt{t'/\log(t')}.$$
Competing effects:
(1) Core threshold increases;
(2) degree increases.
Strong control of $\text{deg}_{t'}(q_{t,0})$:
Using Móri-martingale, Doob's maximal inequality:
$\text{deg}_{t'}(q_{t,0})\gtrsim (t'/t)^{1/(\tau-1)}$ for all $t'>t$ .
$k_{t'}\le \frac{1}{4}f_\tau(t,t')$.
If $t'=T_t(a)$, # iterations is linear in $a$

Heuristic lower bound

Statement. [J., Komjáthy '22]. For $t$ large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

2. Bound rhs using 'old' methods [Dereich, Mönch, Mörters '12].

Naive guess (similar to upper bound):

1. Find sequence $(t_i)_{i\ge 0}$ at which event changes. Then

$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \leq \sum_i \mathbb{P}\Big(\mathrm{dist}_{t_i}(U_t, V_t)\le f_\tau(t,t_i)-1/\varepsilon\Big).$$

RHS not summable, new machinery needed

Heuristic lower bound

Statement. [J., Komjáthy '22]. For $t$ large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

Main idea: Exploit time-dependencies in the growing graph

There is a first time of failure.

Heuristic lower bound

Statement. [J., Komjáthy '22+]. For $t$ sufficiently large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

$\leq C/(t'\log^3(t'))$

Let $\mathcal{E}(t,t'):= \{\mathrm{dist}_{t'}(U_t, V_t)\ge f_\tau(t,t')-1/\varepsilon\}$. Then

$\mathbb{P}\Big(\neg\mathcal{E}(t,t') \mid \bigcap_{\tilde{t}=t}^{t'-1} \mathcal{E}(t,\tilde{t}) \Big)\le\mathbb{P}\big($there is a short path that traverses $t'\big)$

Main idea: Time-dependencies in the growing graph

There is a first time of failure: $f_\tau(t,t') \searrow$.

$$\mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) = \mathbb{P}\big(\neg \mathcal{E}(t,t)\big) + \sum_{t'=t+1}^\infty\mathbb{P}\bigg(\neg\mathcal{E}(t,t') \mid \bigcap_{\tilde{t}=t}^{t'-1} \mathcal{E}(t,\tilde{t}) \bigg)$$

$$\mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \leq \varepsilon + \sum_{t'=t+1}^\infty C/(t'\log^3(t')) \overset{t\to\infty}\longrightarrow \varepsilon$$

$\vdots$

computations,

inductive proves, etc ...

Q2. For $\tau\in(2,3)$, identify $f_\tau(t, t')$ s.t.

$$\Bigg(\sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f_\tau(t, t')\right|\Bigg)_{t\ge 0}$$ is a tight sequence.

Solves main question

Thm. [J., Komjáthy, '22].

$$f_\tau(t,t') = 4\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 2.$$

Weighted distances.
Control added weight added in each iteration.

Open questions

Other evolving properties
- triangles
- colorings
- distance when $\tau>3$ (even static case open)
# edges on shortest $L$-path if $\sup\{x: F_L(x)>0\}=0$
- ?? logarithmic if $L$ explosive ??
fluctuations around main terms

Thank you!

Heuristic upper bound

Weaker statement. [J., Komjáthy '22].
For $t$ large, there $\exist$ nice $t'\mapsto\varepsilon_{t'}$

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 0, $t'=t$:

$^{(t)}$

$^{(t')}$

bounded-length segments

Weighted distance evolution

Weighted version (Evolution statement). [J., Komjáthy '22].
Let $\tau\in(2,3)$, and pick conservative edge-weight distribution $F_L$. Then,

$$\Big(\sup_{t'\ge t}|d^{(L)}_{t'}(U_t, V_t) - f_{\tau}^{(L)}(t,t')|\Big)_{t\geq 0}$$

forms a tight sequence of random variables, where

$$f_\tau^{(L)}(t,t')=2\sum_{k=f_\tau^{(1)}(t,t)-f_\tau(t,t')+1}^{f_\tau(t,t)}F_{L_1+L_2}^{(-1)}\big(\exp(-(\tau-2)^{-k/2})\big),$$

and

f_\tau(t,t') = 2\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 1.

Intuition

Two consecutive terms correspond to minimal weight added in one iteration of the upper bound.
Let $X_1,\dots, X_n$ be i.i.d. random variables. Then $$\min\{X_1,\dots,X_n\}\approx F_L^{(-1)}(1/n).$$
Graph distance drops: largest term removed from sum.

Distance Evolutions in

Preferential Attachment Models

Joost Jorritsma

joint with Júlia Komjáthy

(Random Struct. & Alg. '20, Ann. of Applied Probability '22+)

MiSe ETH Zürich

March 2022

arXiv: tiny.cc/DistanceEvolutionPAM

Guiding 'real-world' example

Internet network: communicating routers and servers

~1969: 2 connected sites (UCLA, SRI)

Time

~1971: 15 connected sites

~1989: 0.5 million users

~2020: billions of connected devices

Evolving/dynamic network:
- Vertices arrive over time.
- Connect to present vertices.
- (Nodes may be removed or replaced.)
- (Edges between 'old' vertices are removed or placed.)
[Faloutsos, Faloutsos & Faloutsos, '99]:
- # connections per router decays as power-law: $p_k\sim k^{-\tau}, \tau>2$.
- Short average hopcount between routers.

Guiding 'real-world' example

Internet network: communicating routers and servers

Evolving network: Vertices arrive over time, connect to present vertices.
[Faloutsos, Faloutsos & Faloutsos, '99]: Short average hopcount.

1999

$\mathrm{dist}_{\color{red}{'99}}(u_{'99}, v_{'99}) = 4$

2005

$\mathrm{dist}_{{\color{red}'05}}(u_{'99}, v_{'99}) = 3$

2022

$\mathrm{dist}_{{\color{red}'22}}(u_{'99}, v_{'99}) = 2$

How does hopcount between old nodes change in growing network?

$u_{'99}$

$v_{'99}$

Preferential attachment models

Definition

Start with a single vertex
Vertices enter the network one-by-one at discrete (time-)steps $t=2, 3,...$.
New vertex connects to old vertices according to some increasing function of the degree:
- Fixed outdegree: $(m,\delta): m$ edges/new vertex ($\delta>-m$):
  $$\mathbb{P}\big(v_{t+1} \overset{j}{\longrightarrow} v_i\big) \propto \mathrm{deg}_{t,j}(v_i) + \delta/m.$$
- Variable outdegree: $\forall v_i \in \mathrm{PA}_t$, independently, ($\gamma,\eta\in(0,1)$)
  $$\mathbb{P}\big(v_{t+1} \longrightarrow v_i\big) = (\gamma \mathrm{deg}_{t}(v_i)+\eta)/t.$$
Animation

Many dependencies:

Edge added at time $t$ depends on earlier edges, influences later added edges

Thm. [Bollobás, Riordan, Spencer, Tusnády '01; Dereich, Mörters '09]

Limiting degree distribution decays as power-law: for $\tau_{m,\delta}=3+\delta/m; \tau_\gamma=1+1/\gamma$,

$$p_k \sim k^{-\tau}.$$

Distances on PAMs

Thm. [Dereich, Mönch, Mörters '12].

For $\tau\in(2,3)$, $U_t, V_t\sim \text{Unif(Largest cluster}(t))$:

$$\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t}) \asymp 4\frac{\log\log(t)}{|\log(\tau-2)|} $$

Thm. [Dommers, v/d Hofstad, Hooghiemstra '10].

For $\tau>3$, $\exists c_1, c_2>0$:

$$c_1\preccurlyeq\frac{\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t})}{\log(t)} \preccurlyeq c_2.$$

Thm. [Bollobás, Riordan '04; Dereich, Mönch, Mörters '17].

For $\tau=3$:

$$\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t})\asymp \frac{\log(t)}{\log\log(t)}.$$

Thm. [Dereich, Mönch, Mörters '12; J., Komjáthy '20].

For $\tau\in(2,3)$, $U_t, V_t\sim \text{Unif(Largest cluster}(t))$:

$$\bigg(\left|\mathrm{dist}_{{\color{red}t}}(U_{\color{blue}t}, V_{\color{blue}t}) - 4\frac{\log\log(t)}{|\log(\tau-2)|}\right|\bigg)_{t\ge 0} $$

is a tight sequence of random variables ($\forall \varepsilon>0 \exists M(\varepsilon)\forall t: \mathbb{P}(|Y_t|\ge M)<\varepsilon$).

Literature perspective on PAMs

Many static/limiting properties are well-understood
- Degree distribution.
- Typical graph distance.
- Diameter of the graph.
- Local neighborhood of a typical vertex (local weak sense).
- Component sizes.
- ...
- ...
Studying static properties allows for comparison to static (non-growing) models (configuration model, Norros-Reittu, ...).
Theorem statements do not display dynamics inherently present in PAMs (contrary to proofs).
- Exception: degree evolution $(\mathrm{deg}_{t'}(v))_{t'\ge v}$ of (sets of) fixed vertices.

Goal: try to understand how the graph evolves for $t'\ge t$ from perspective of graph at time $t$

Main Question

Consider $\Big(\big(\mathrm{dist}_{{\color{red}t'}}(U_{\color{blue} t}, V_{\color{blue} t})\big)_{{\color{red}t'}\ge {\color{blue}t}}\Big)_{t\ge 0}$ and define for a function $f(t,t')$

$$X_t^f := \sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f(t, t')\right|.$$

Q1. For $\tau\in(2,3)$, can we identify $f_\tau(t, t')$ s.t.

$(X_t^{f_\tau})_{t\ge 0}$ is a tight sequence?

$\mathrm{dist}_{t_0}(U_{t_0}, V_{t_0}) = 7,$

$\mathrm{dist}_{t_1}(U_{t_0}, V_{t_0}) = 6,$

$0$

$t_2$

$\mathrm{dist}_{t_2}(U_{t_0}, V_{t_0}) = 2$

$U_{t_0}$

$V_{t_0}$

$t_1$

$t_0$

Q2. For $\tau\in(2,3)$, identify $f_\tau(t, t')$ s.t.

$$\Big(\sup_{t'\ge t}\left| \mathrm{dist}_{{\color{red}t'}}(U_{\color{blue}t}, V_{\color{blue}t}) - f_\tau(t, t')\right|\Big)_{t\ge 0}$$ is a tight sequence.

Main Theorem

Thm. [J., Komjáthy, '22+].

$$f_\tau(t,t') = 4\frac{\log\log(t) - \log(1\vee\log(t'/t))}{|\log(\tau-2)|}\vee 2.$$

Corollary. Hydrodynamic limit [J., Komjáthy '22+].
Let $t'=T_t(a):=t\exp\big(\log^a(t)\big)$ for $a\in[0,1]$, then

$$f_\tau(t,T_t(a)) = 4(1-a)\frac{\log\log(t)}{|\log(\tau-2)|}\vee 2,$$ and

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.$$

Main Theorem

Corollary. Hydrodynamic limit [J., Komjáthy '22+].
Let $t'=T_t(a):=t\exp\big(\log^a(t)\big)$ for $a\in[0,1]$, then

$$ \sup_{a\in[0,1]} \left| \frac{\mathrm{dist}_{T_t(a)}(U_t, V_t)}{\log\log(t)} - (1-a)\frac{4}{|\log(\tau-2)|}\right|\overset{\mathbb{P}}{\longrightarrow} 0.$$

Heuristic upper bound

Statement. [J., Komjáthy '22+].

For $\tau\in(2,3)$,
$$ \mathbb{P}\Big(\forall t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')+1/\varepsilon\Big) \ge 1-\varepsilon. $$

Weaker statement. [J., Komjáthy '22+].
For $t$ large, there $\exist$ nice $t'\mapsto\varepsilon_{t'}$

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')+1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

"Proof" of statement by smart union bound.

Consider $(t_i(t))_{i\ge 0}$ at integer crossings rhs (i.e., event changes).
Distance is non-increasing.
By weak version, the statement follows if for $t$ large $\sum_i \varepsilon_{t_i(t)} \leq \varepsilon$.
Weak statement follows from minor adaptations of [Dommers, v/d Hofstad, Hooghiemstra '10; Dereich, Mönch, Mörters '12; Caravenna, Garavaglia, v/d Hofstad '19; J., Komjáthy '20].

Unfortunately $\int_t^\infty \varepsilon_{t'} \mathrm{d}t'\to \infty.$

Naive idea: Union bound.

Heuristic upper bound

Weaker statement. [J., Komjáthy '22+].
For $t$ large, there $\exist$ nice $t'\mapsto\varepsilon_{t'}$

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 0, $t'=t$:

$^{(t)}$

$^{(t')}$

bounded-length segments

Heuristic upper bound

Weaker statement. [J., Komjáthy '22+].
For $t$ large, there $\exist$ nice $t'\mapsto\varepsilon_{t'}$

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 0, $t'=t$:

$\mathrm{deg}_t(\cdot)$

$\mathrm{Core}(t)$

$\text{Core}(t'):=\{v\le t': \text{deg}_{(1-\varepsilon)t'}(v)\ge \sqrt{t'/\log(t')}\}$.
If $\mathrm{deg}_{(1-\varepsilon)t'}(x)=s: \exists y: \mathrm{deg}_{(1-\varepsilon)t'}(y)\approx s^{1/(\tau-2)}, \{x\overset{2}{\leftrightarrow} y\}_{t'}$.
# of iterations needed to reach core: smallest $k_t$ s.t.
$$\big(\mathrm{deg}_{t'}(q_{t_0})\big)^{1/(\tau-2)^k} \ge \sqrt{t/\log(t)}.$$
$k_t\approx\log\log(t)/|\log(\tau-2)|=\frac{1}{4}f_\tau(t,t)$ iterations for $U_t, V_t$.

Heuristic upper bound

Weaker statement. [J., Komjáthy '22+].
For $t$ large, there $\exist$ nice $t'\mapsto\varepsilon_{t'}$

$$ \mathbb{P}\Big(\mathrm{dist}_{t'}(U_t, V_t)\le f_{\tau}(t,t') + 1/\varepsilon\Big) \ge 1-\varepsilon_{t'}. $$

Step 1, $t'>t$:

$\mathrm{deg}_t(\cdot)$

$\mathrm{Core}(t)$

$\mathrm{deg}_{t'}(\cdot)$

$\mathrm{Core}(t')$

$\text{Core}(t'):=\{v\le t': \text{deg}_{(1-\varepsilon)t'}(v)\ge \sqrt{t'/\log(t')}\}$.
If $\mathrm{deg}_{(1-\varepsilon)t'}(x)=s: \exists y: \mathrm{deg}_{(1-\varepsilon)t'}(y)\approx s^{1/(\tau-2)}, \{x\overset{2}{\leftrightarrow} y\}_{t'}$.
# of iterations needed: smallest $k_{t'}$ s.t.
$$\big(\mathrm{deg}_{t'}(q_{t_0})\big)^{1/(\tau-2)^k} \ge \sqrt{t'/\log(t')}.$$
Competing effects:
(1) Core threshold increases;
(2) degree increases.
Strong control of $\text{deg}_{t'}(q_{t,0})$:
Using Móri-martingale, Doob's maximal inequality:
$\text{deg}_{t'}(q_{t,0})\gtrsim (t'/t)^{1/(\tau-1)}$ for all $t'>t$ .
$k_{t'}\le \frac{1}{4}f_\tau(t,t')$.
If $t'=T_t(a)$, # iterations is linear in $a$

Heuristic lower bound

Statement. [J., Komjáthy '22+]. For $t$ sufficiently large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

2. Bound rhs using 'old' methods [Dereich, Mönch, Mörters '12].

Naive guess (similar to upper bound):

1. Find sequence $(t_i)_{i\ge 0}$ at which event changes. Then

$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \leq \sum_i \mathbb{P}\Big(\mathrm{dist}_{t_i}(U_t, V_t)\le f_\tau(t,t_i)-1/\varepsilon\Big).$$

RHS not summable, new machinery needed

Heuristic lower bound

Statement. [J., Komjáthy '22+]. For $t$ sufficiently large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

Main idea: Exploit time-dependencies in the growing graph

There is a first time of failure.

Heuristic lower bound

Statement. [J., Komjáthy '22+]. For $t$ sufficiently large
$$ \mathbb{P}\Big(\exist t'\ge t: \mathrm{dist}_{t'}(U_t, V_t)\le f_\tau(t,t')-1/\varepsilon\Big) \le \varepsilon. $$

*In fact, we need a more advanced separation of events (using good and bad paths, inspired by [Dereich, Mönch, Mörters '12]) that makes the decomposition more interlinked.

$\leq^\ast C/(t'\log^3(t'))$

Let* $\mathcal{E}(t,t'):= \{\mathrm{dist}_{t'}(U_t, V_t)\ge f_\tau(t,t')-1/\varepsilon\}$. Recall $f_\tau(t,t')$ is non-increasing. Then

$\mathbb{P}\Big(\neg\mathcal{E}(t,t') \mid \bigcap_{\tilde{t}=t}^{t'-1} \mathcal{E}(t,\tilde{t}) \Big)\le\mathbb{P}\big($there is a short path that traverses $t'\big)$

Main idea: Exploit time-dependencies in the growing graph

There is a first time of failure.

$\vdots$

computations,

inductive proves, etc ...

Weighted distance in PAM

Ex.: Many distributions with support starting at 0 are explosive: Unif[0,1], Exp($\lambda$).

Threshold: $L$ is explosive if close to 0 for some $\beta>1$

$$F_L(x)\ge\exp\big(-\exp\big(x^{-\beta}\big)\big).$$

Def. Weighted distance: $d_{t'}^{(L)}(x, y):= \min_{\pi \text{ from }x\text{ to }y \text{ at time }t'} \sum_{e\in\pi} L_e$

Weighted version (Static statement). [J., Komjáthy '20].
Let $\tau\in(2,3)$. Equip every edge with i.i.d. $L_e\ge 0$ with cdf $F_L$, $U_t, V_t\sim \text{Unif(Largest cluster}(t))$.

If $F_L$ satisfies

$$\sum_{k=1}^\infty F_L^{(-1)}\big(\exp(-e^k)\big) < \infty,$$

then $d_t^{(L)}(U_t, V_t)\to \beta^{(1)}+ \beta^{(2)}$, with $\mathbb{P}(\beta^{(i)}<\infty)=1$.

Otherwise, if $L$ is not too flat, then we identify $f^{(L)}_\tau(t,t)$ such that $$\Big(d_t^{(L)}(U_t, V_t)-f^{(L)}_\tau(t,t)\Big)_{t\ge 0}$$ is a tight sequence.

Main theorem (general version)

Weighted version (Evolution statement). [J., Komjáthy '20+].
Let $\tau\in(2,3)$. Equip every edge with i.i.d. $L_e\ge 0$, $U_t, V_t\sim \text{Unif(Largest cluster}(t))$. If $F_L^{(-1)}$ is not extremely flat, then

$$\Big(\sup_{t'\ge t}|d^{(L)}_{t'}(U_t, V_t) - f_{\tau}^{(L)}(t,t')|\Big)_{t\geq 0}$$

forms a tight sequence of random variables, where

$$f_\tau^{(L)}(t,t')=2\sum_{k=(f_\tau(t,t)-f_\tau(t,t'))/4}^{(f_\tau(t,t))/4}F_{L_1+L_2}^{(-1)}\big(\exp(-(\tau-2)^{-k})\big).$$

Def. Weighted distance: $d_{t'}^{(L)}(x, y):= \min_{\pi \text{ from }x\text{ to }y \text{ at time }t'} \sum_{e\in\pi} L_e$

Intuition

Every term corresponds to minimal weight added in one iteration.
Let $X_1,\dots, X_n$ be i.i.d. random variables. Then $$\min\{X_1,\dots,X_n\}\approx F_L^{(-1)}(1/n).$$
Graph distance drops: largest term removed from sum.

MiSe Distance evolutions

By joostjor

Distance Evolutions in

Preferential Attachment Models

Guiding 'real-world' example

Guiding 'real-world' example

Preferential attachment models

Distances on PAMs

Static properties in PAMs

Main Question

Main Theorem

Main Theorem

Back to static: weighted distance

Weighted distance: a game

Weighted distance: a game

Explosive weights

Conservative weights

Explosion: Intuition

Convservative: Intuition

Weighted-distance evolution

Heuristic upper bound

Heuristic upper bound

Heuristic upper bound

Heuristic upper bound

Heuristic lower bound

Heuristic lower bound

Heuristic lower bound

Solves main question

Open questions

Thank you!

Heuristic upper bound

Weighted distance evolution

Distance Evolutions in

Preferential Attachment Models

Guiding 'real-world' example

Guiding 'real-world' example

Preferential attachment models

Distances on PAMs

Literature perspective on PAMs

Main Question

Main Theorem

Main Theorem

Heuristic upper bound

Heuristic upper bound

Heuristic upper bound

Heuristic upper bound

Heuristic lower bound

Heuristic lower bound

Heuristic lower bound

Weighted distance in PAM

Main theorem (general version)

MiSe Distance evolutions

More from joostjor