Naresh Kumar Devulapally
But why is Diffusion?
Naresh Kumar Devulapally
From basics of Distributions to Diffusion Models

CSE 573: CVIP
Naresh Kumar Devulapally

Introduction


Generative models have gotten very powerful recently
Stable Diffusion generated images
stabilityai/stable-diffusion-xl-base-1.0
stabilityai/stable-diffusion-3.5-medium
CSE 573: CVIP
Naresh Kumar Devulapally

What to expect from these lectures?
- Introduction to Generative models (the intuition)
- Understanding of the DDPM paper
- Ability to read through diffusion-based papers after the lectures.
CSE 573: CVIP
Naresh Kumar Devulapally

What is a Function?
In mathematics, a function from a set \( X \) to a set \( Y \) assigns to each element of \( X \) exactly on element of \( Y \).
- Wikipedia
In simpler words, a function is something that takes an input and maps only one possible output for that given input.
Generally, a function is represented using \( f(\cdot) \), and a function that maps a point \(x \in X \) to \( y \in Y \) is represented as:
CSE 573: CVIP
Naresh Kumar Devulapally

What is a Function?
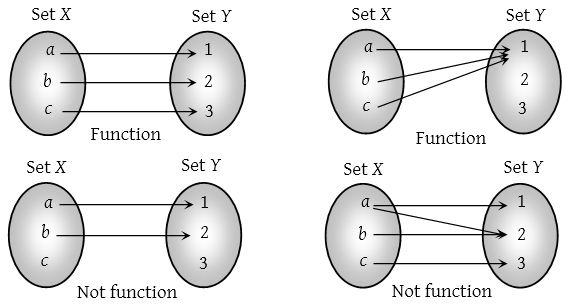
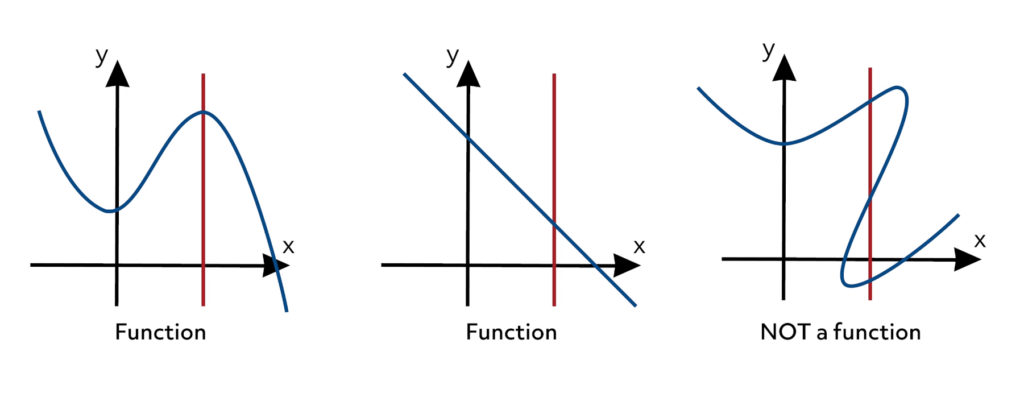
CSE 573: CVIP
Naresh Kumar Devulapally

Why do we need Function?
Let's say you are given a bunch of data points:
CSE 573: CVIP
Naresh Kumar Devulapally
CSE 4/573 Computer Vision

Why do we need Function?
Let's say you are given a bunch of data points:
Mar 11, 2025
Naresh Kumar Devulapally

Why do we need Function?
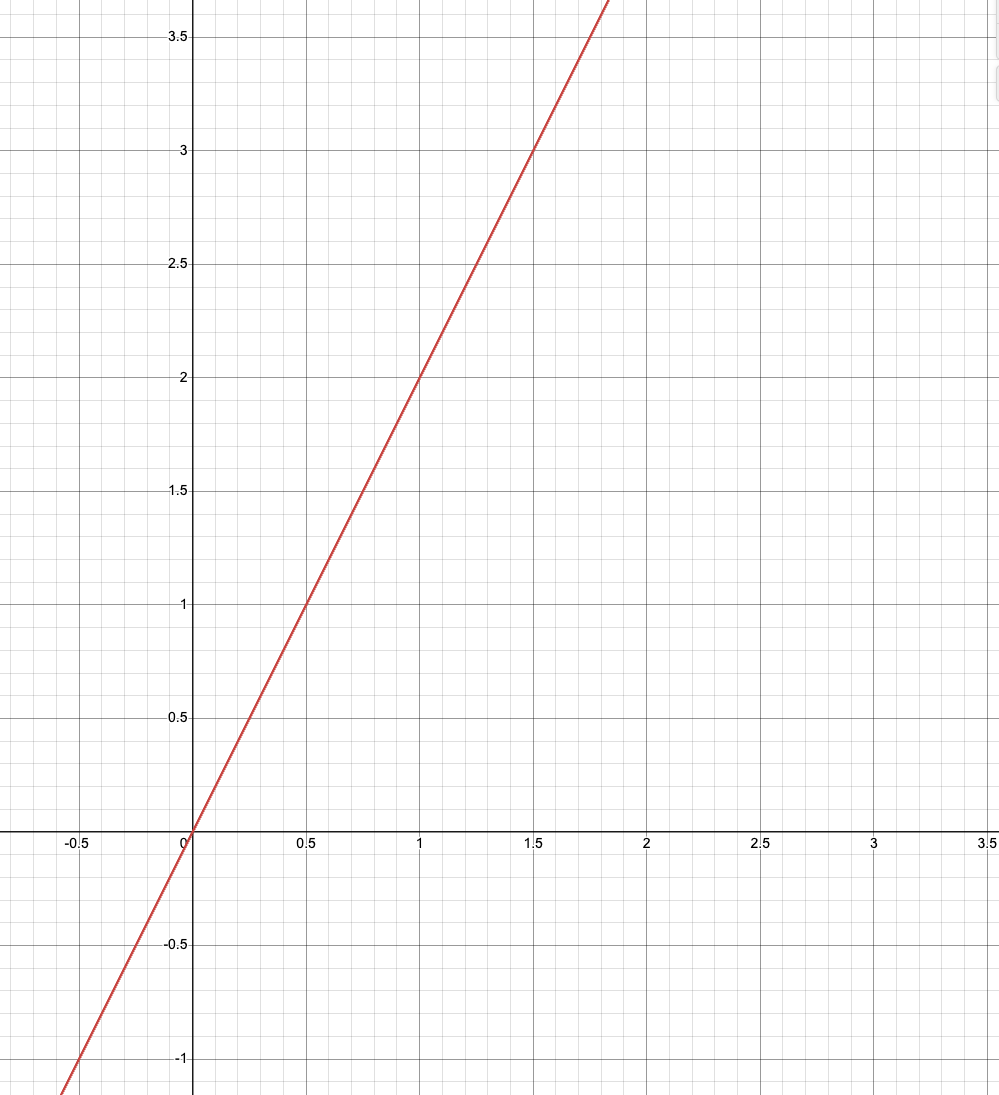
CSE 573: CVIP
Naresh Kumar Devulapally

Why do we need Function?
There are many ways to estimate a function \( y = f(x) \) based on data points. Discussion of such methods is outside the scope of this lecture.
However, we will touch upon basics of powerful function approximators, known as:
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Estimating Function?
There are many ways to estimate a function \( y = f(x) \) based on data points. Discussion of such methods is outside the scope of this lecture.
However, we will touch upon basics of powerful function approximators, known as:
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

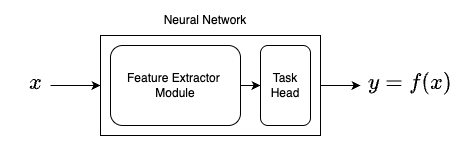
Neural Networks have two components:
- Feature Extractor Module
- Task specific head
You can experiment with simple neural networks at Tensorflow Playground
Mar 11, 2025
CSE 555: Pattern Recognition
Estimating a Function
Naresh Kumar Devulapally

Estimating a Function
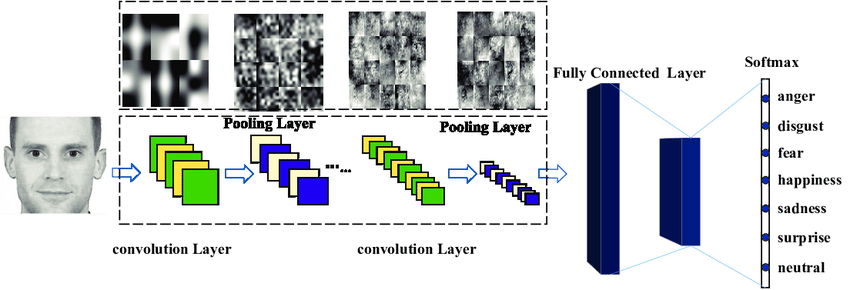
A simple example of a Neural Network
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Estimating a Function
Mar 11, 2025
CSE 555: Pattern Recognition
We have very powerful discriminator models:
- E.g., Image classification models
What about generative models?
Given a label (e.g., "cat"), can we
generate a data point (image)?
Naresh Kumar Devulapally

From functions to data
Where does your sample come from?
Mar 11, 2025
CSE 555: Pattern Recognition



Let's shift our focus from labels to data points.
Naresh Kumar Devulapally

From functions to data
Where does your sample come from?
Mar 11, 2025
CSE 555: Pattern Recognition



unknown
Naresh Kumar Devulapally

Whats a Probability Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
Eg: Flipping a fair coin
- Heads
- Tails
Naresh Kumar Devulapally

Whats a Probability Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
We can ask questions like:
- How many times will \( X \) be equal to \(1\) if I flip a coin \( 1000 \) times?
- Can we even expect some pattern?
- Why? Why not?
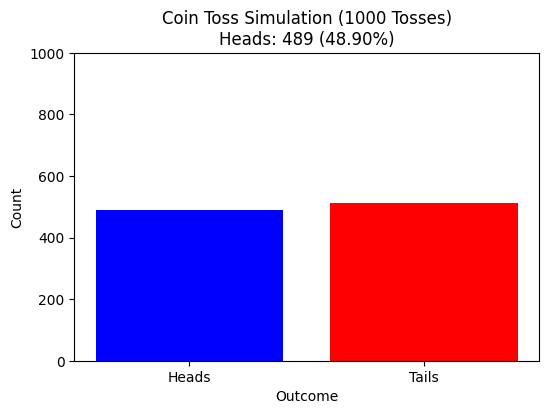
Naresh Kumar Devulapally

Whats a Probability Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
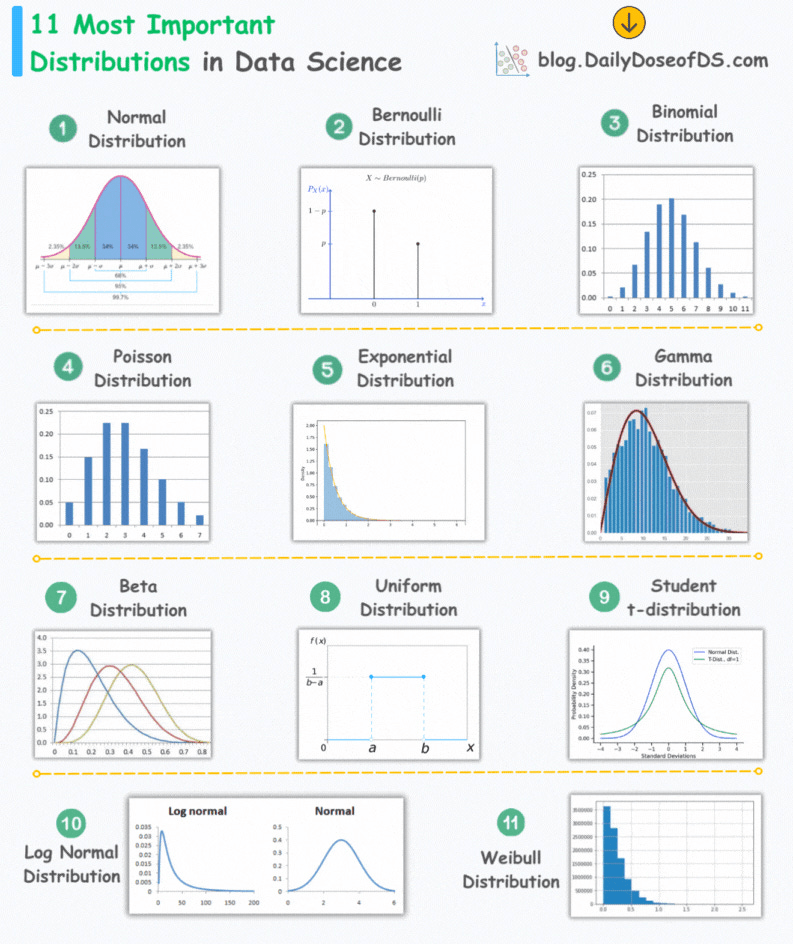
Naresh Kumar Devulapally

Whats a Probability Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
Mean - \( \mu \)
Variance - \( \sigma^2 \)
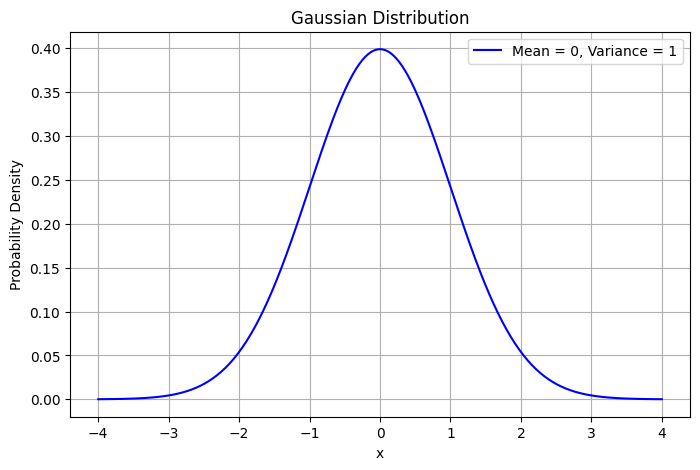
Naresh Kumar Devulapally

Whats a Probability Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
Mean - \( \mu \)
Variance - \( \sigma^2 \)
change
Naresh Kumar Devulapally

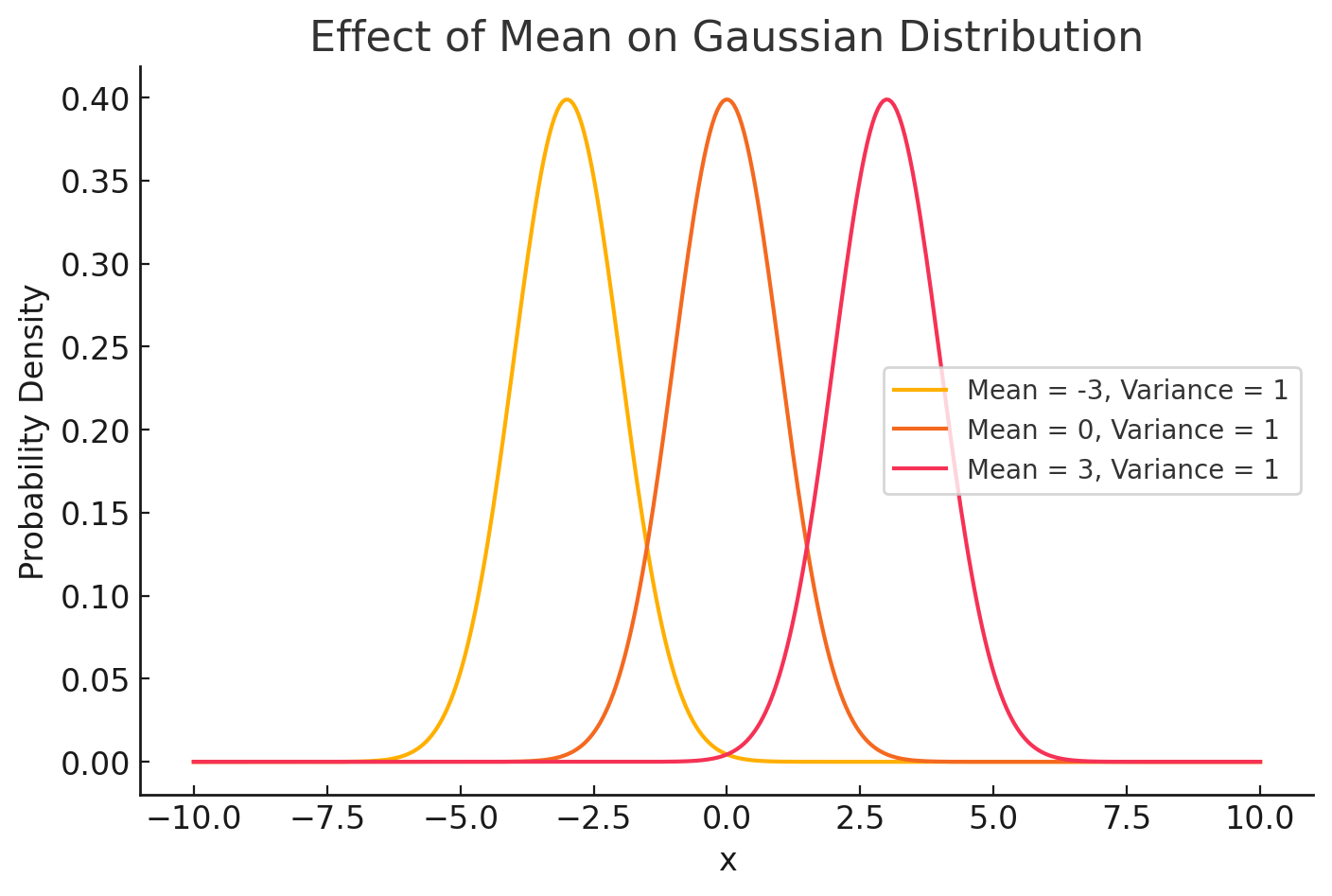
Whats a Probability Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
Mean - \( \mu \)
Variance - \( \sigma^2 \)
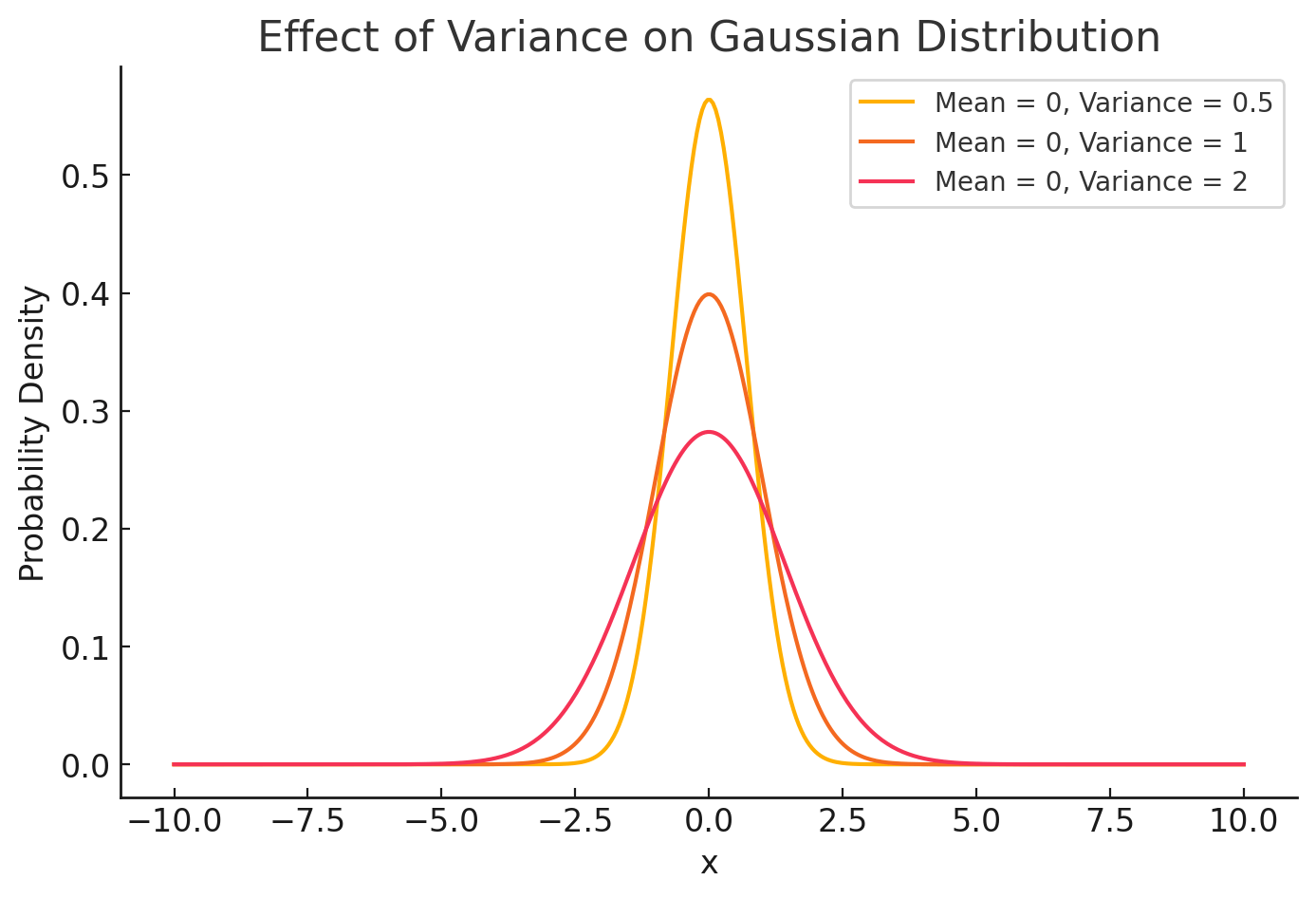
change
Naresh Kumar Devulapally

Whats a Probability Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
Mean - \( \mu \)
Variance - \( \sigma^2 \)

\( x \) follows a normal distribution with mean \( \mu \) and variance \( \sigma^2 \)
Naresh Kumar Devulapally

Gaussian Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition

Mean - \( \mu \)
Variance - \( \sigma^2 \)
Naresh Kumar Devulapally

Gaussian Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
Mean - \( \mu \)
Variance - \( \sigma^2 \)
All of these denote Gaussian distributions
A sample from the above distribution:
Naresh Kumar Devulapally

Gaussian Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
Suppose \( x_1 \sim \mathcal{N}(\mu_1, \sigma_1^2 I) \) and \( x_2 \sim \mathcal{N}(\mu_2, \sigma_2^2 I) \).
What is the distribution of \( x_1 + x_2 \)?
Naresh Kumar Devulapally

Gaussian Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
Suppose \( x_1 \sim \mathcal{N}(\mu_1, \sigma_1^2 I) \) and \( x_2 \sim \mathcal{N}(\mu_2, \sigma_2^2 I) \).
What is the distribution of \( x_1 + x_2 \)?
Suppose \( \boldsymbol{\varepsilon}_1, \boldsymbol{\varepsilon}_2 \sim \mathcal{N}(0, I) \), and
\( \boldsymbol{x}_1 = \sigma_1 \boldsymbol{\varepsilon}_1 \quad \text{and} \quad \boldsymbol{x}_2 = \sigma_2 \boldsymbol{\varepsilon}_2 \)
\( \boldsymbol{x}_1 + \boldsymbol{x}_2 \sim \mathcal{N}(0, (\sigma_1^2 + \sigma_2^2)I) \).
\( \boldsymbol{x}_1 + \boldsymbol{x}_2 = \sqrt{\sigma_1^2 + \sigma_2^2} \, \boldsymbol{\varepsilon} \)
sample
Naresh Kumar Devulapally

Gaussian Distribution?
Mar 11, 2025
CSE 555: Pattern Recognition
Product of two Gaussians is a Gaussian
Naresh Kumar Devulapally

Estimating data distribution
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Estimating data distribution
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Estimating data distribution
Mar 11, 2025
CSE 555: Pattern Recognition

Boo!! (You know nothing about me)
Naresh Kumar Devulapally

Estimating data distribution
Mar 11, 2025
CSE 555: Pattern Recognition

our friend
Let's condition \( P(x) \) on \( P(z) \) and assume \( x \) comes from \(z\). But Why?! and How?!
Posterior
Generative Model
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
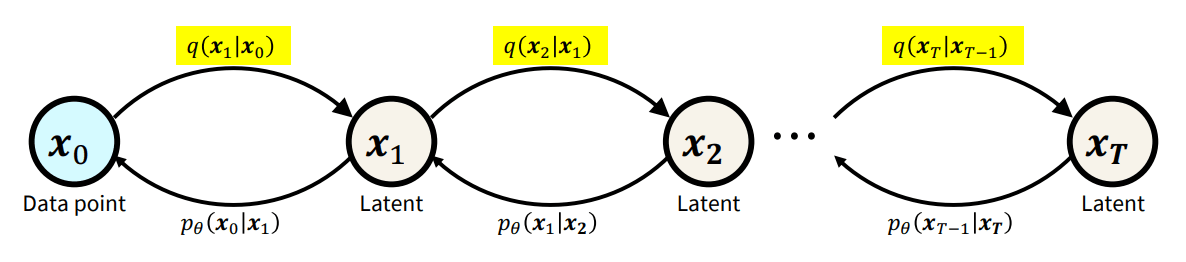
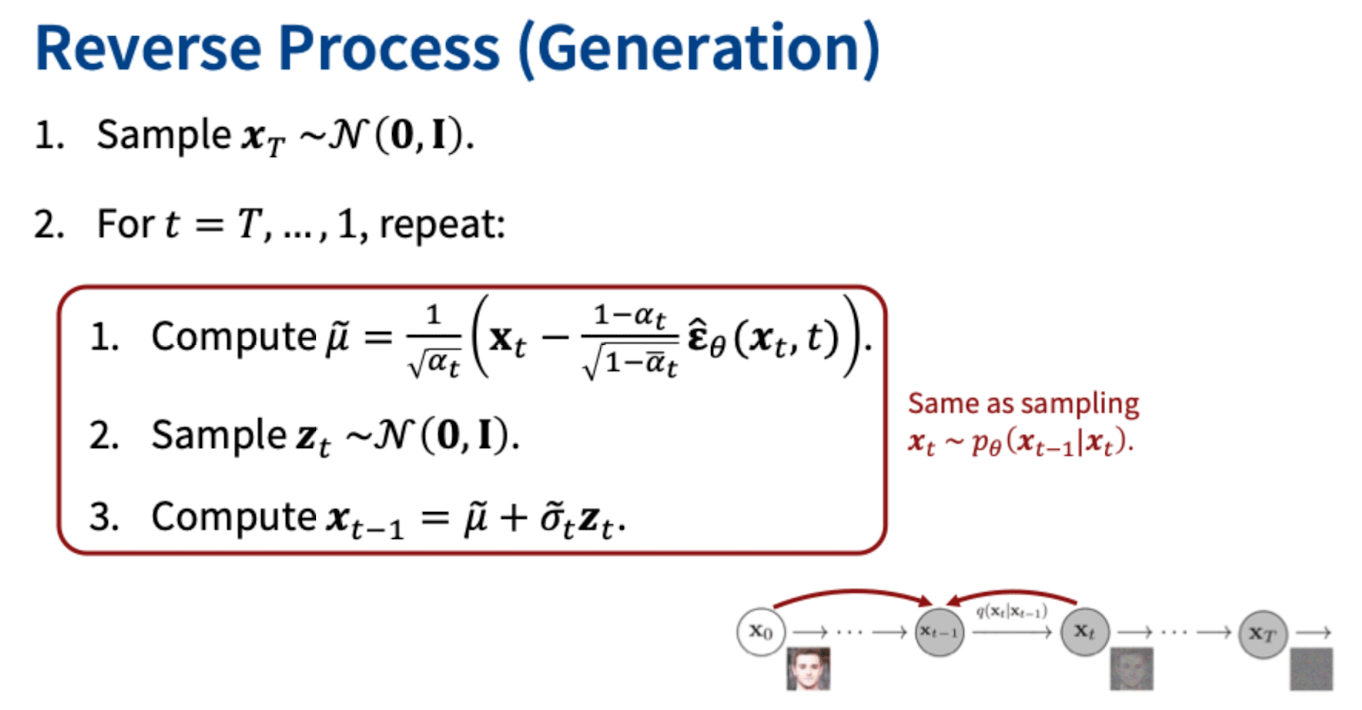
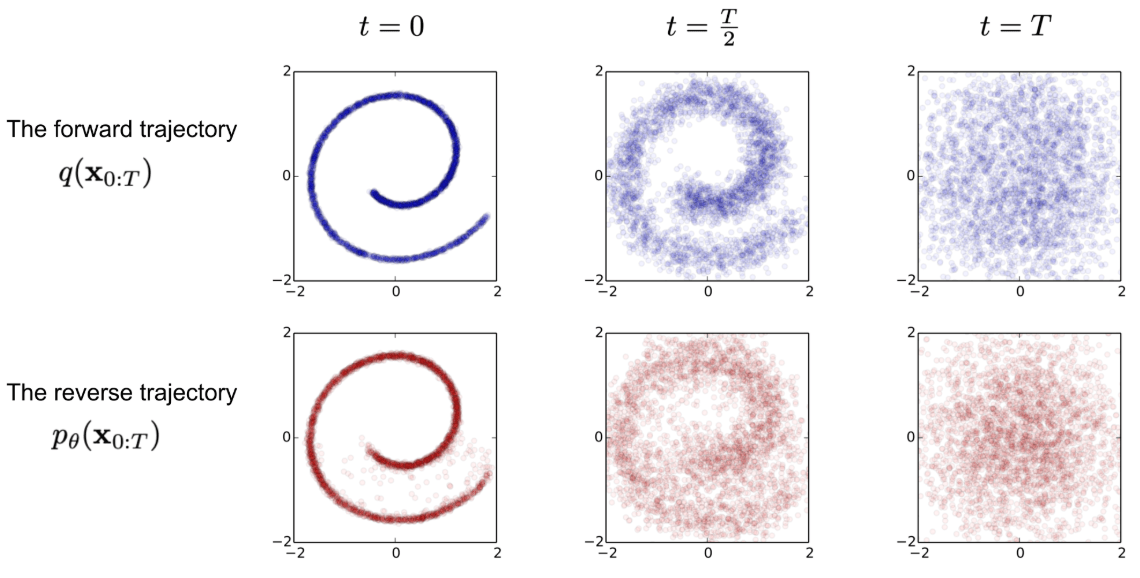
- Forward Process
- Reverse Process
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Why multiple steps in forward process?

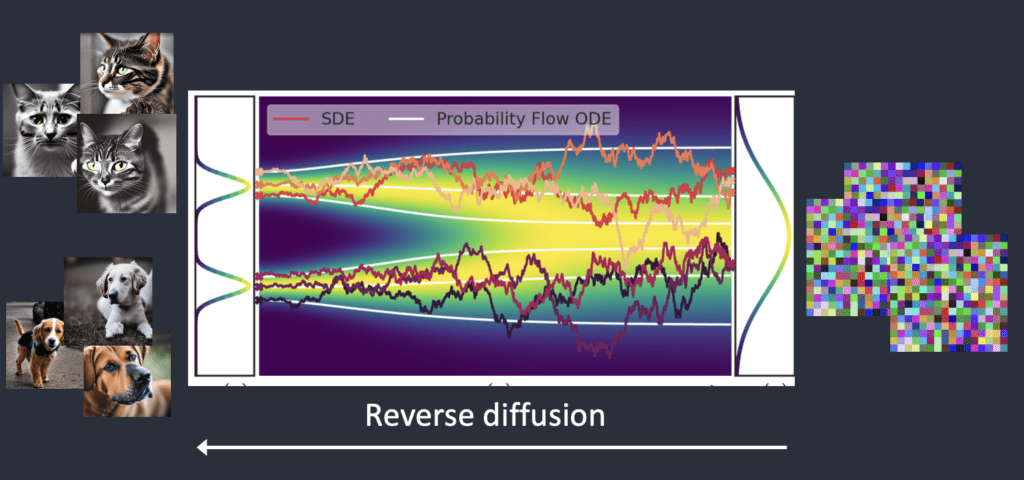
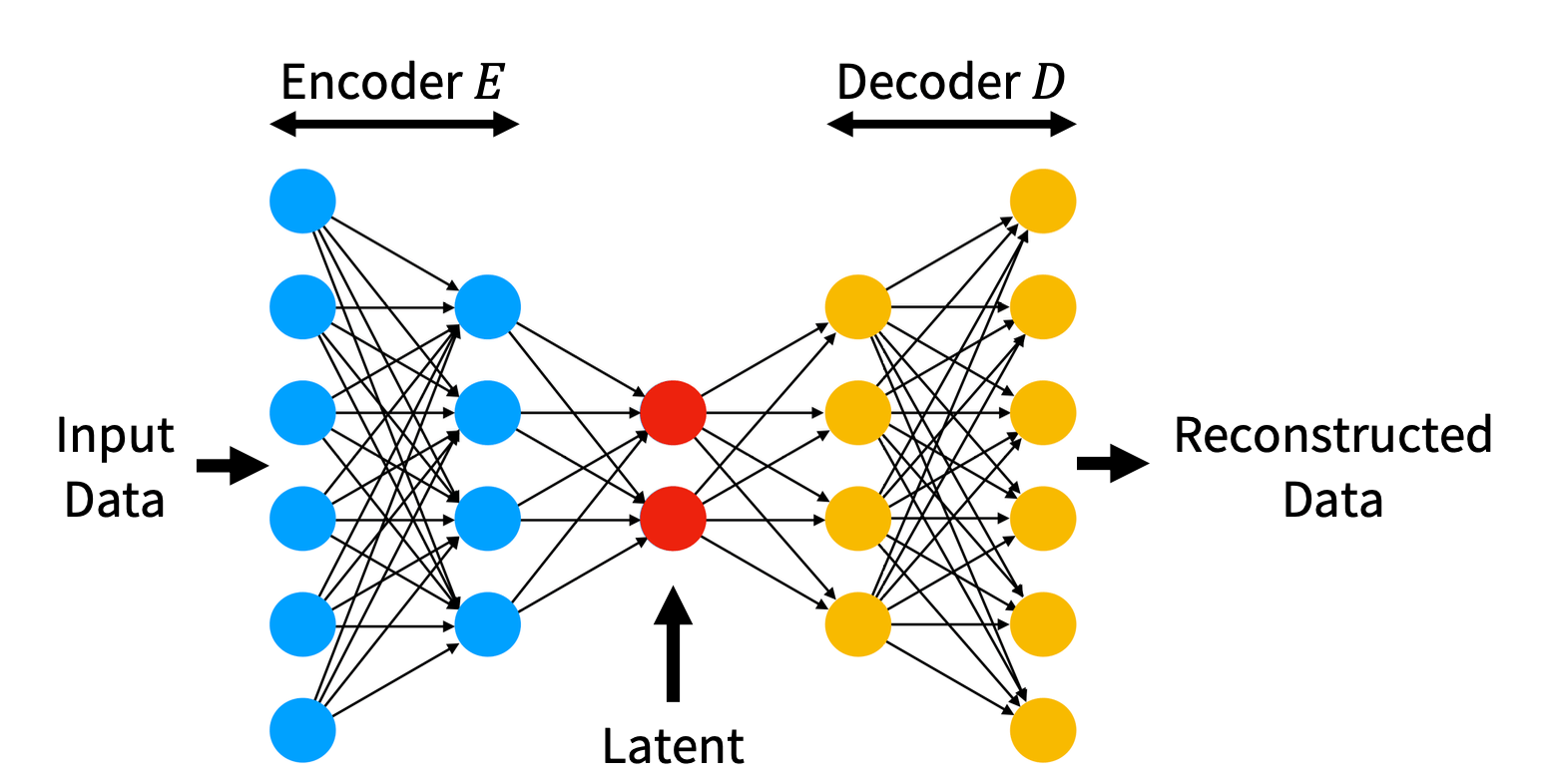
Data reconstruction using VAEs
Concept of trajectories in Diffusion models
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Posterior
Generative Model
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
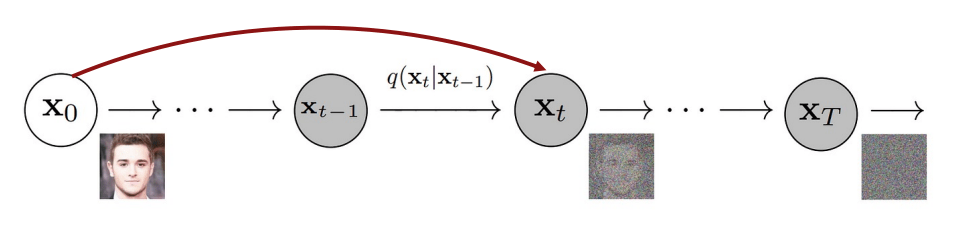
In the forward process, the transition distribution \( q(x_t \mid x_{t-1}) \) is specifically predefined as:
where \( { \beta_t \in (0, 1) }_{t=1}^T \) and \( \beta_1 \leq \beta_2 \leq ... \leq \beta_T \)
"Adding Gaussian Noise iteratively"
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Choices of \( \beta_t \)
- Learned
- Constant
- Linearly or quadratically increasing
- Cosine function
Note that the reverse step \( p_\theta (x_{t-1} \mid x_t ) \) becomes Gaussian form only when \( \beta_t \) is small \( ( \beta_t << 1 ) \).
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Choices of \( \beta_t \)
- Learned
- Constant
- Linearly or quadratically increasing
- Cosine function
Note that the reverse step \( p_\theta (x_{t-1} \mid x_t ) \) becomes Gaussian form only when \( \beta_t \) is small \( ( \beta_t << 1 ) \).
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Yes! Under certain conditions that we are now going to define.
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Yes! Under certain conditions that we are now going to define.
where \( { \beta_t \in (0, 1) }_{t=1}^T \) and \( \beta_1 \leq \beta_2 \leq ... \leq \beta_T \)
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Let \( \alpha_t = 1 - \beta_t \)
where \( { \alpha_t \in (0, 1) }_{t=1}^T \) and \( \alpha_1 \geq \alpha_2 \geq ... \geq \alpha_T \)
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Can we derive \( q ( x_t \mid x_0 ) \) from the sequence of \( q( x_t' \mid x_{t'-1} ) \) ?
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
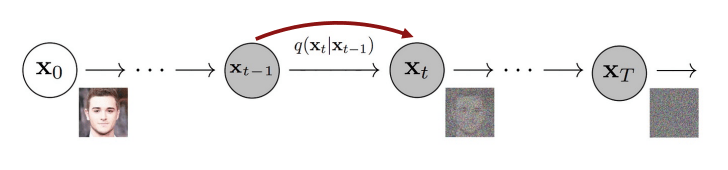
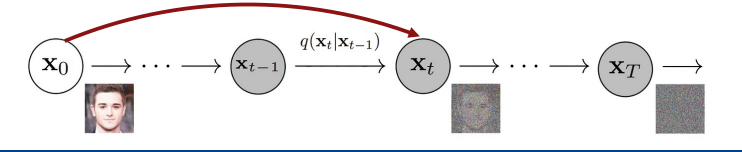
What is the distribution of \( q(x_2 \mid x_0) \) ?
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
When \( { \beta_t \in (0, 1)}_{t=1}^T \) what is:
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
As \( T \to \infty \), \( q(x_T \mid x_0) \) converges to the standard normal distribution:
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition

DDPM generated images
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
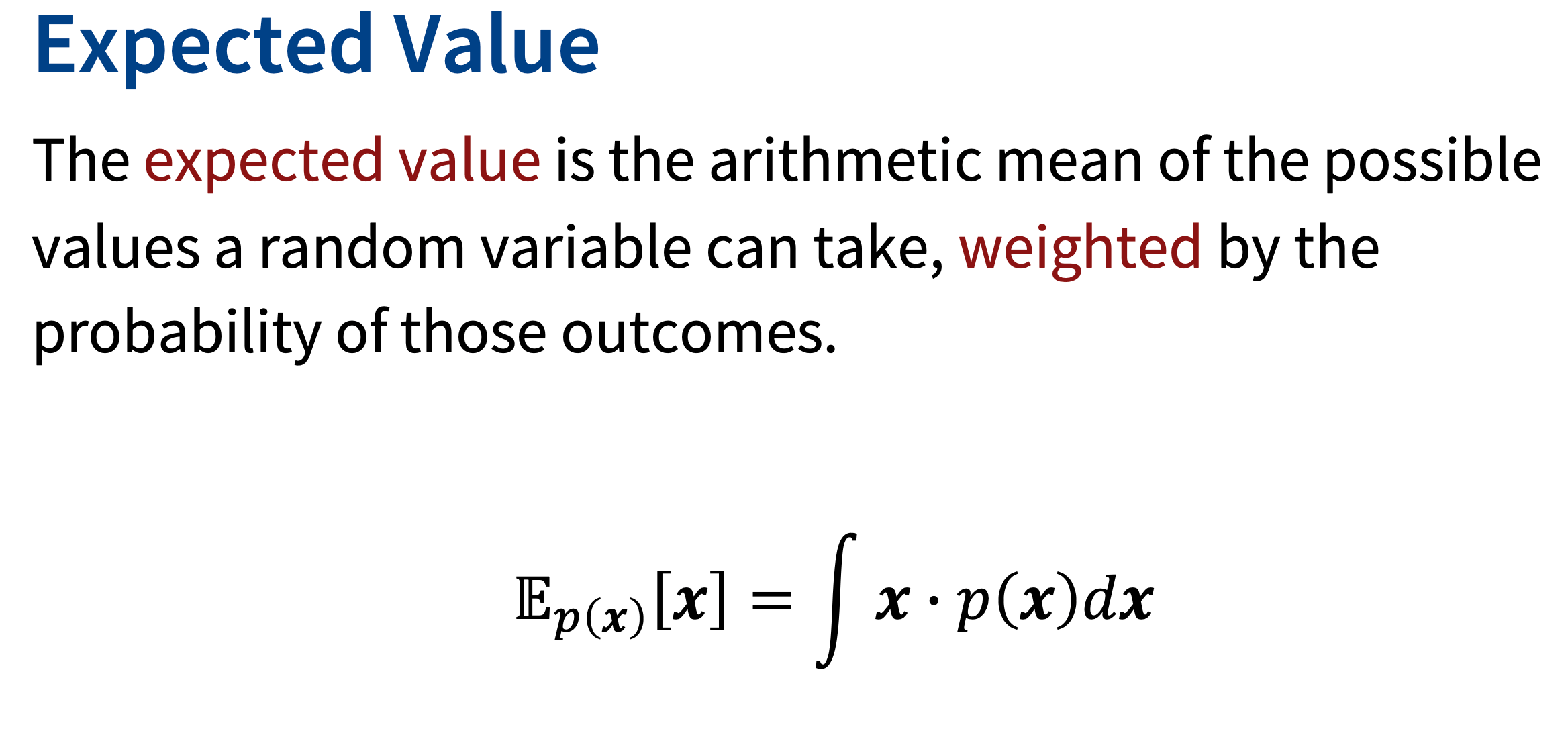
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition

Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition

Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
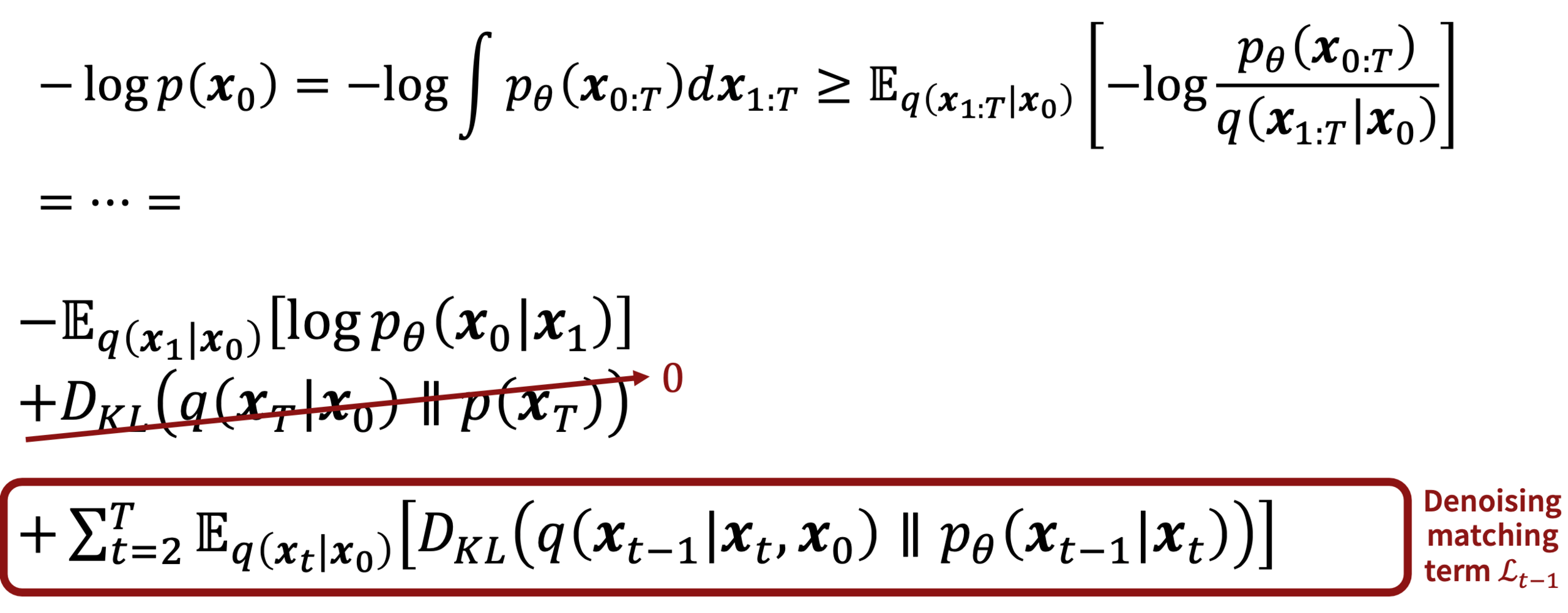
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
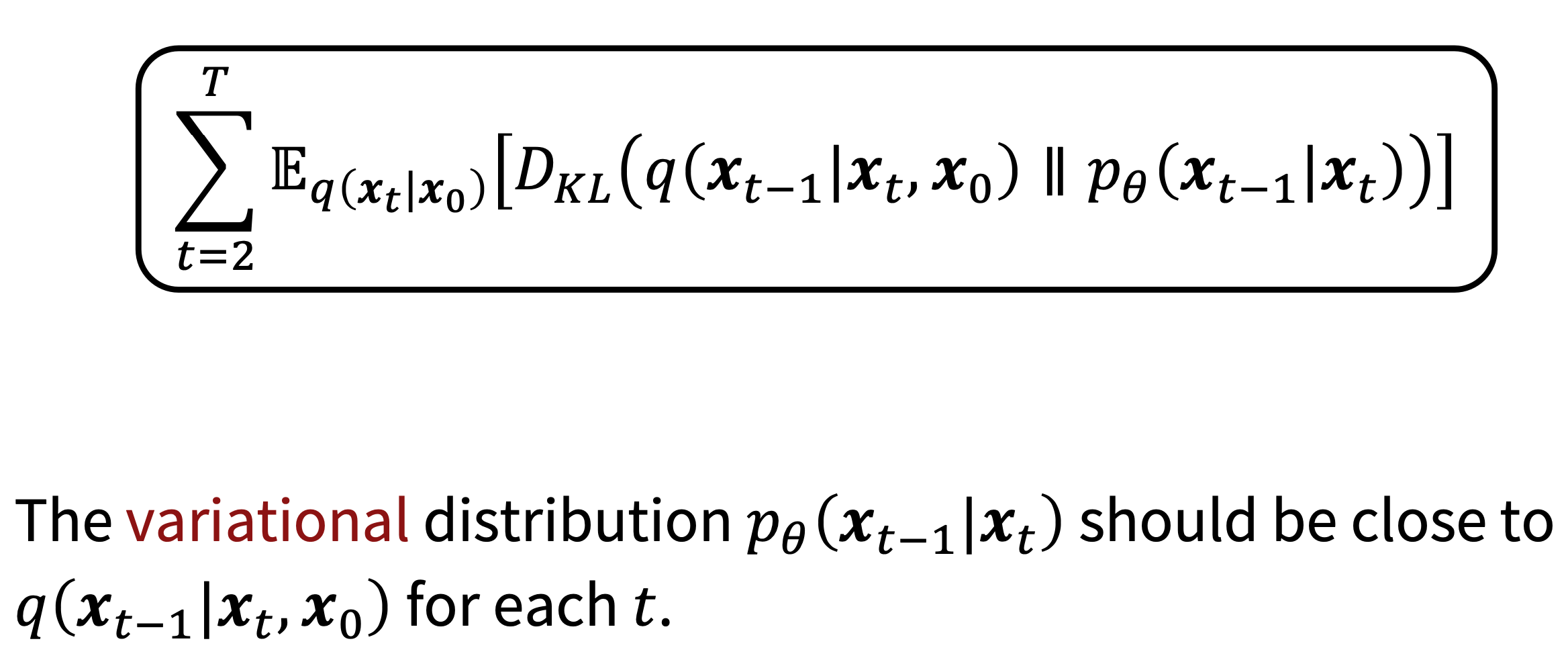
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition

Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition

Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition

Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition

Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Diffusion Models
Mar 11, 2025
CSE 555: Pattern Recognition
Naresh Kumar Devulapally

Latent Diffusion Model
Mar 11, 2025
CSE 555: Pattern Recognition
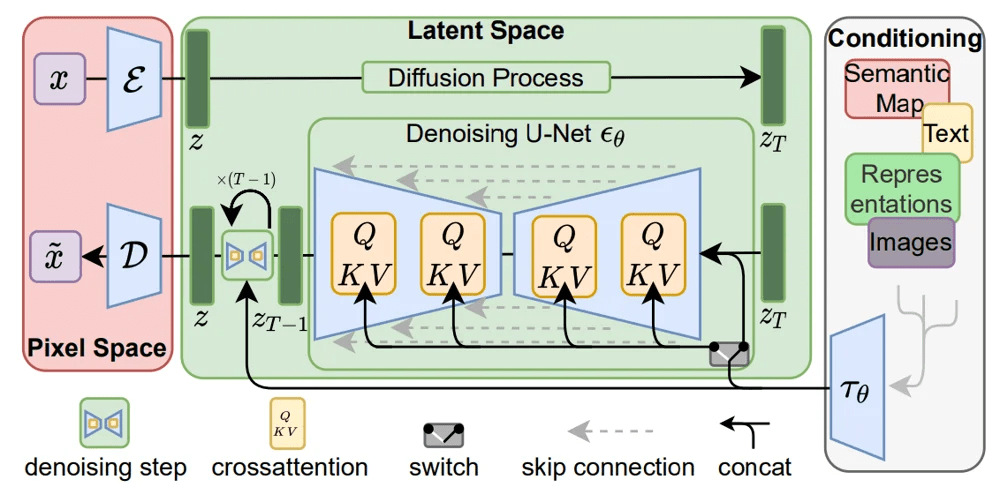
Naresh Kumar Devulapally

Diffusers
Mar 11, 2025
CSE 555: Pattern Recognition
Diffusion Guest Lecture
By Naresh Kumar Devulapally
Diffusion Guest Lecture
Invited Guest Lecture - CSE 555 Pattern Recognition - Fall 2025
- 743



