(Second-)largest component in

spatial inhomogeneous random graphs

Joost Jorritsma

joint with Júlia Komjáthy, Dieter Mitsche

Papers: tiny.cc/cluster-size-ksrg

Cluster-size decay in supercrit. nearest-neighbor percolation

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)=

\exp\big(-\Theta(\sqrt{k})\big)

[Grimmett & Marstrand '90, Kesten & Zhang '90]

Cluster-size decay in supercrit. nearest-neighbor percolation

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)=

\exp\big(-\Theta(k^{\mathbf{\zeta}})\big),\qquad\zeta=\frac{d-1}d

[Grimmett & Marstrand '90, Kesten & Zhang '90]

Cluster-size decay in Erdős–Rényi random graph

\mathbb{P}\big(|{\color{green}\mathcal{C}(0)}|\ge k, 0\notin\mathcal C_n^{(1)}\big)=

\exp\big(-\Theta(k^{\mathbf{\zeta}})\big),\qquad\zeta=1

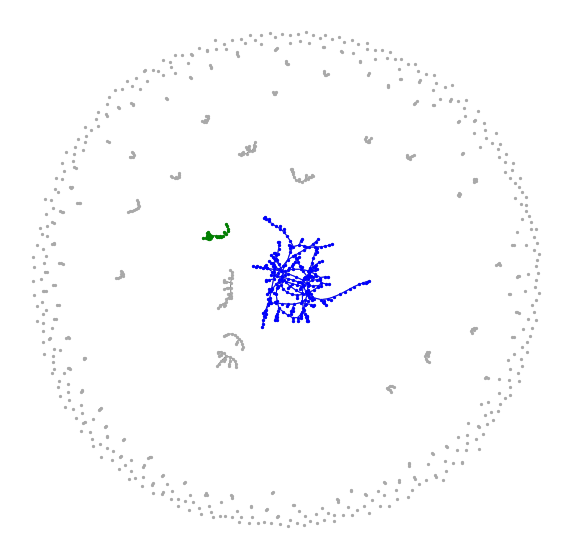
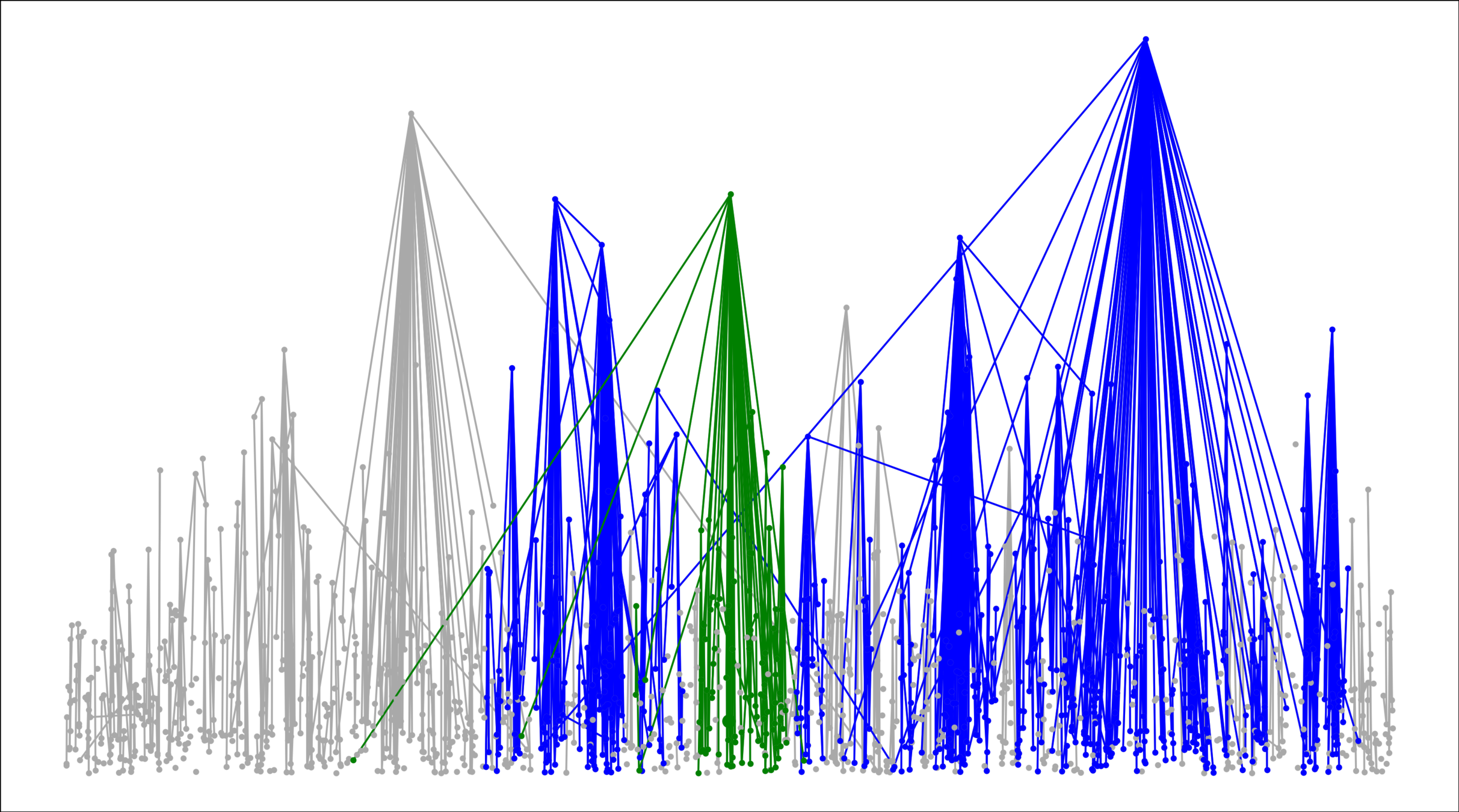
Hyperbolic random graph

Scale-free percolation

Long-range percolation

Scale-free Gilbert RG

Random geom. graph

Nearest-neighbor percolation

Kernel-based spatial random graphs

Vertex set $\mathcal{V}_\infty$

Spatial locations, either
- Lattice $\mathbb{Z}^d$
- Poisson point process (unit intensity)
Power-law i.i.d. weights $w_v\ge 1$:
$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$,

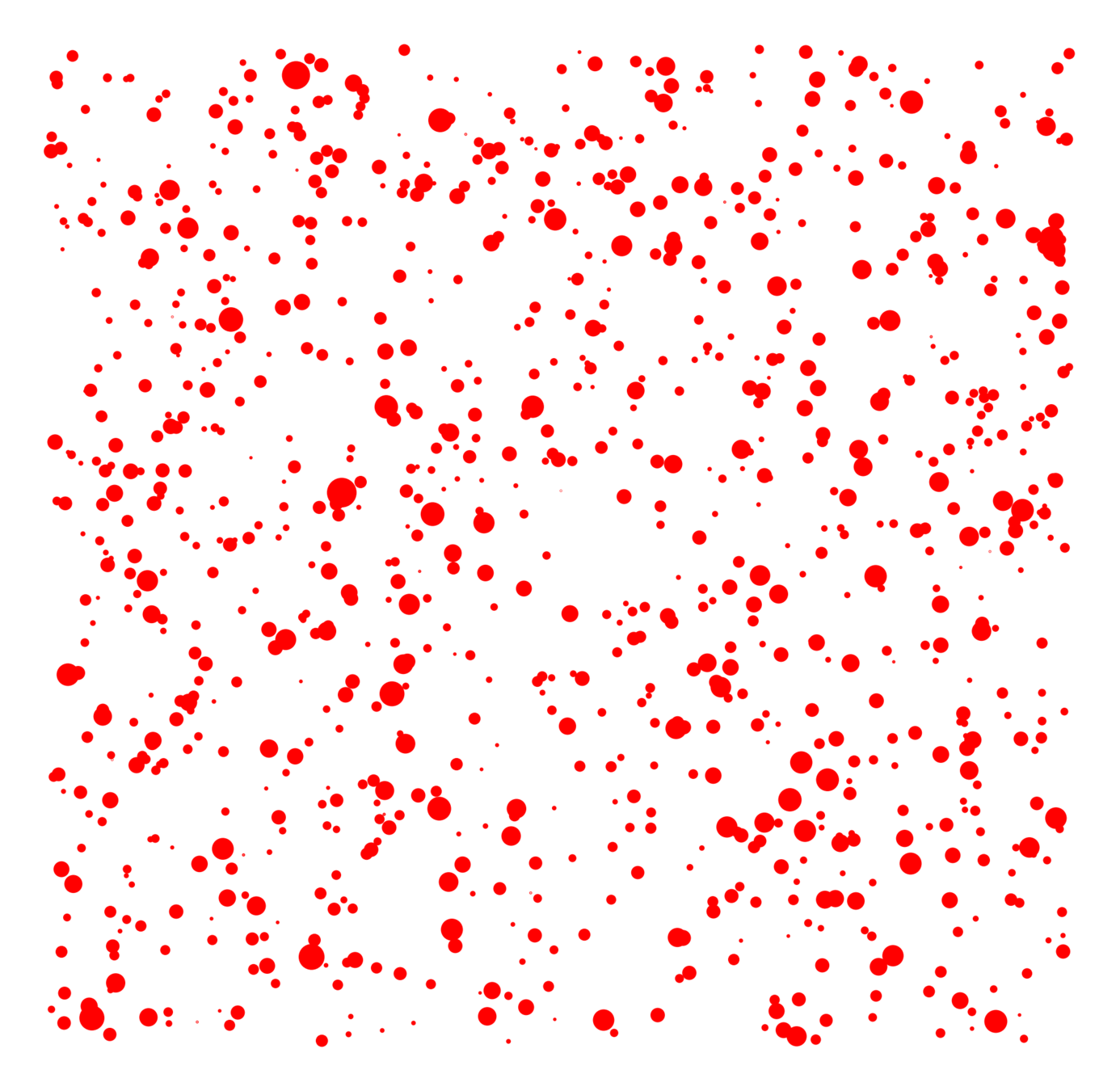
Kernel-based spatial random graphs

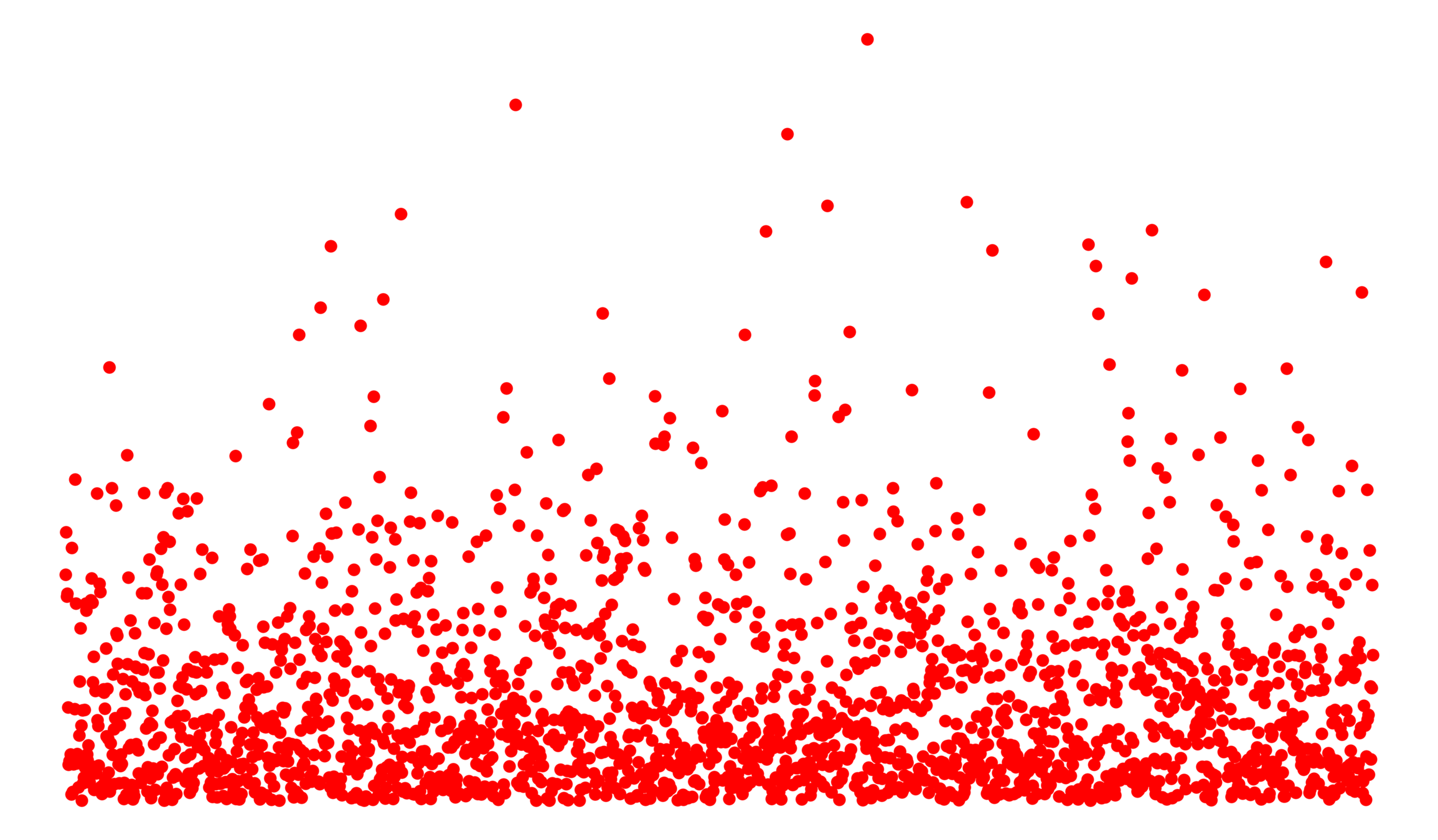
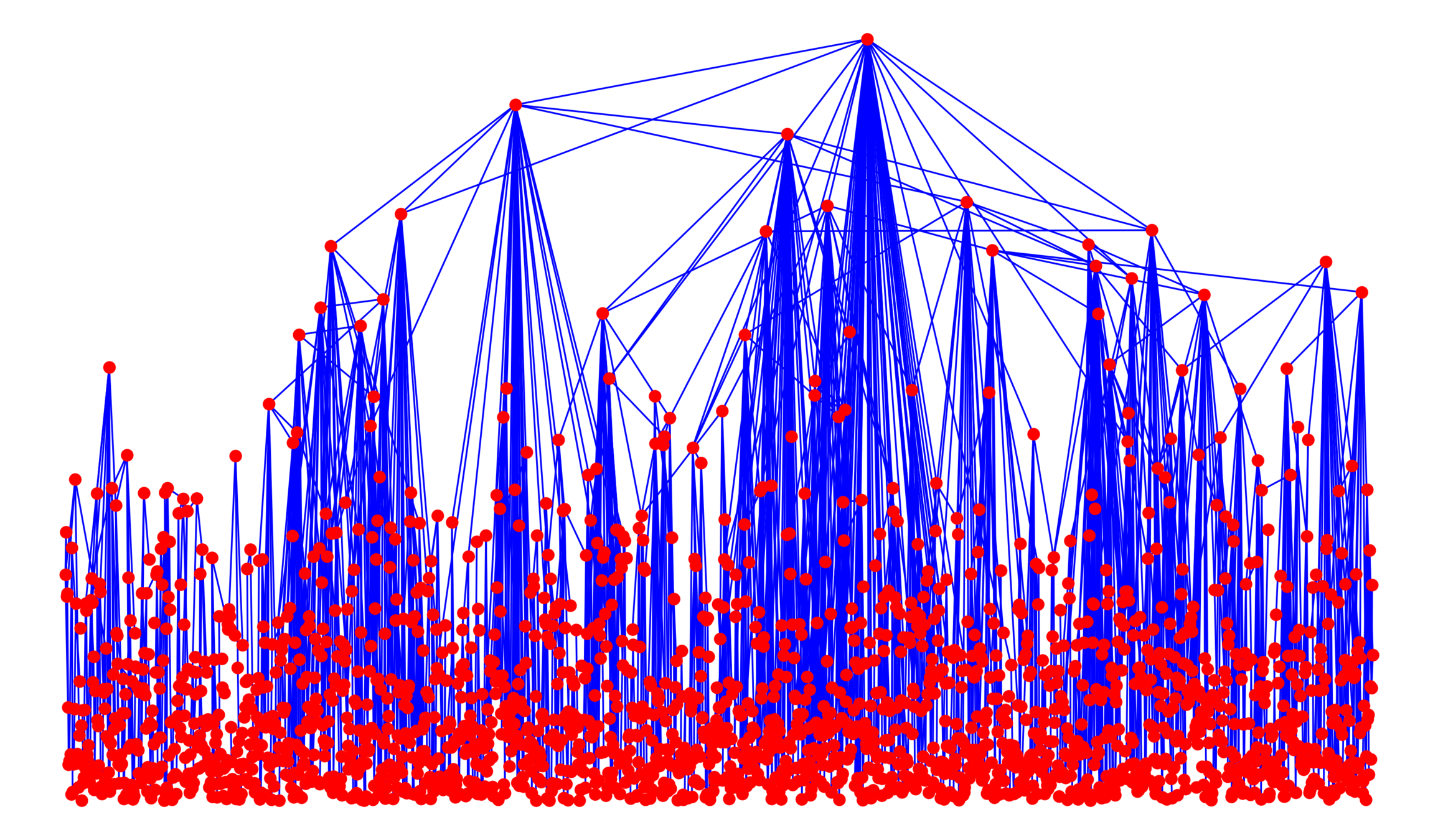
Edge set $\mathcal{E}_\infty$

Symmetric kernel $\kappa(w_u, w_v)$,
Long-range parameter $\alpha\in(1,\infty]$,
Edge-density $\beta>0$,

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1$$

Vertex set $\mathcal{V}_\infty$

Spatial locations, either
- Lattice $\mathbb{Z}^d$
- Poisson point process (unit intensity)
Power-law i.i.d. weights $w_v\ge 1$:
$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$,

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{\bigg(\beta}\frac{\kappa(w_u, w_v)}{\phantom{\|x_u-x_v\|^d}}\phantom{\bigg)^\alpha\wedge 1}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{\bigg(\beta}\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\phantom{\bigg)^\alpha\wedge 1}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\phantom{\beta}\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\phantom{\wedge 1}$$

Kernel-based spatial random graphs

Edge set $\mathcal{E}_\infty$

Symmetric kernel $\kappa(w_1, w_2)$,
Edge-density $\beta>0$,
Long-range parameter $\alpha\in(1,\infty]$,

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1$$

Vertex set $\mathcal{V}_\infty$

Spatial locations, either
- Lattice $\mathbb{Z}^d$
- Poisson point process (unit intensity)
Power-law i.i.d. weights $w_v\ge 1$:
$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}$,

\kappa_\mathrm{prod}=w_uw_v

\alpha\in(1,\infty], d\ge 1

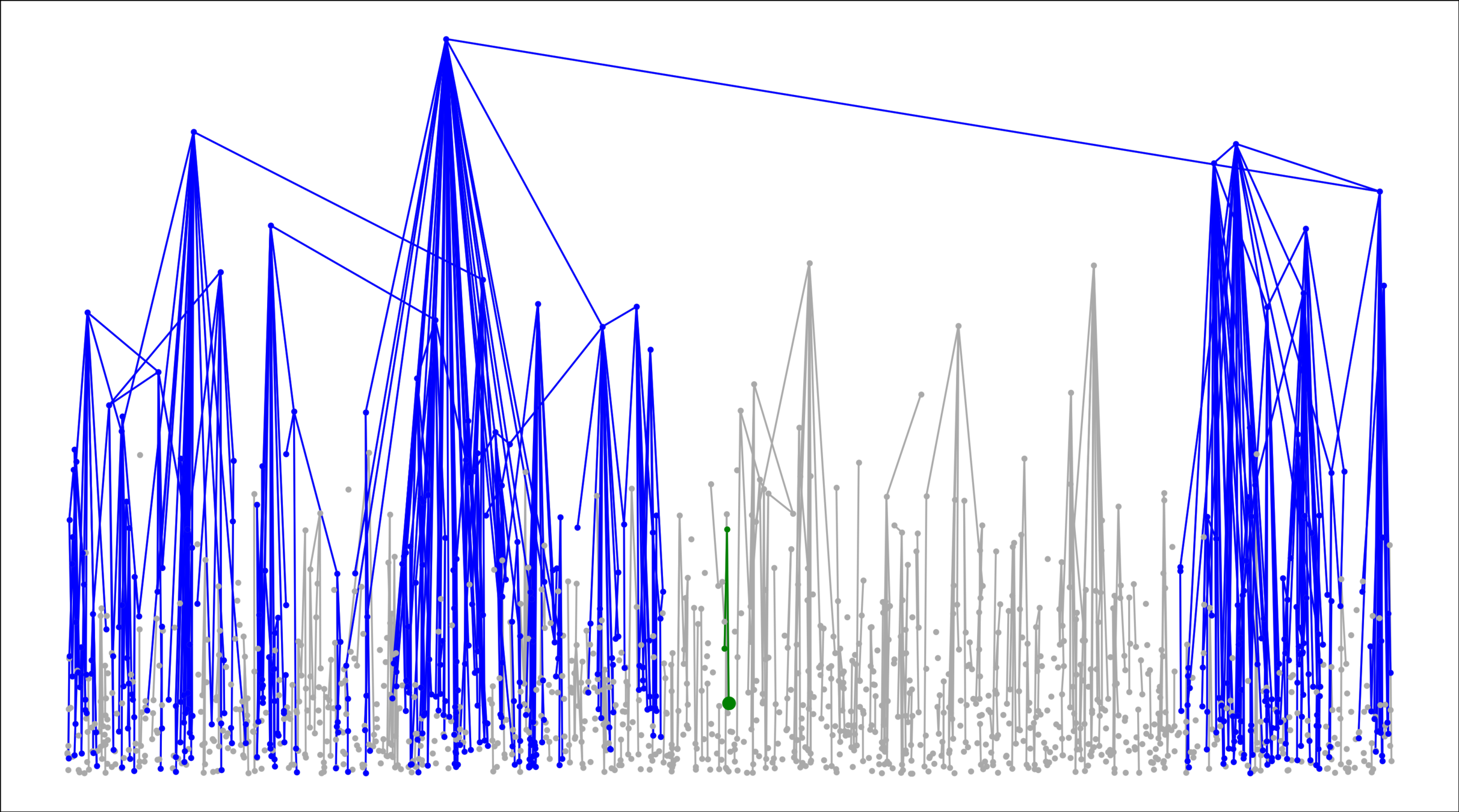
Geom. Inhom. RG

\kappa_\mathrm{prod}=w_uw_v

\alpha=\infty, d= 1

Hyperbolic RG

Geom. RG

\kappa_\mathrm{triv}\equiv 1

\alpha=\infty, d \ge 2

Long-range perc.

\kappa_\mathrm{triv}\equiv 1

\alpha\in(1,\infty), d\ge 1

\kappa_{\max}=w_u\vee w_v

Scale-free Gilbert RG

\kappa_{\mathrm{pa}}=(w_u\vee w_v)

\cdot(w_u\wedge w_v)^{\tau-2}

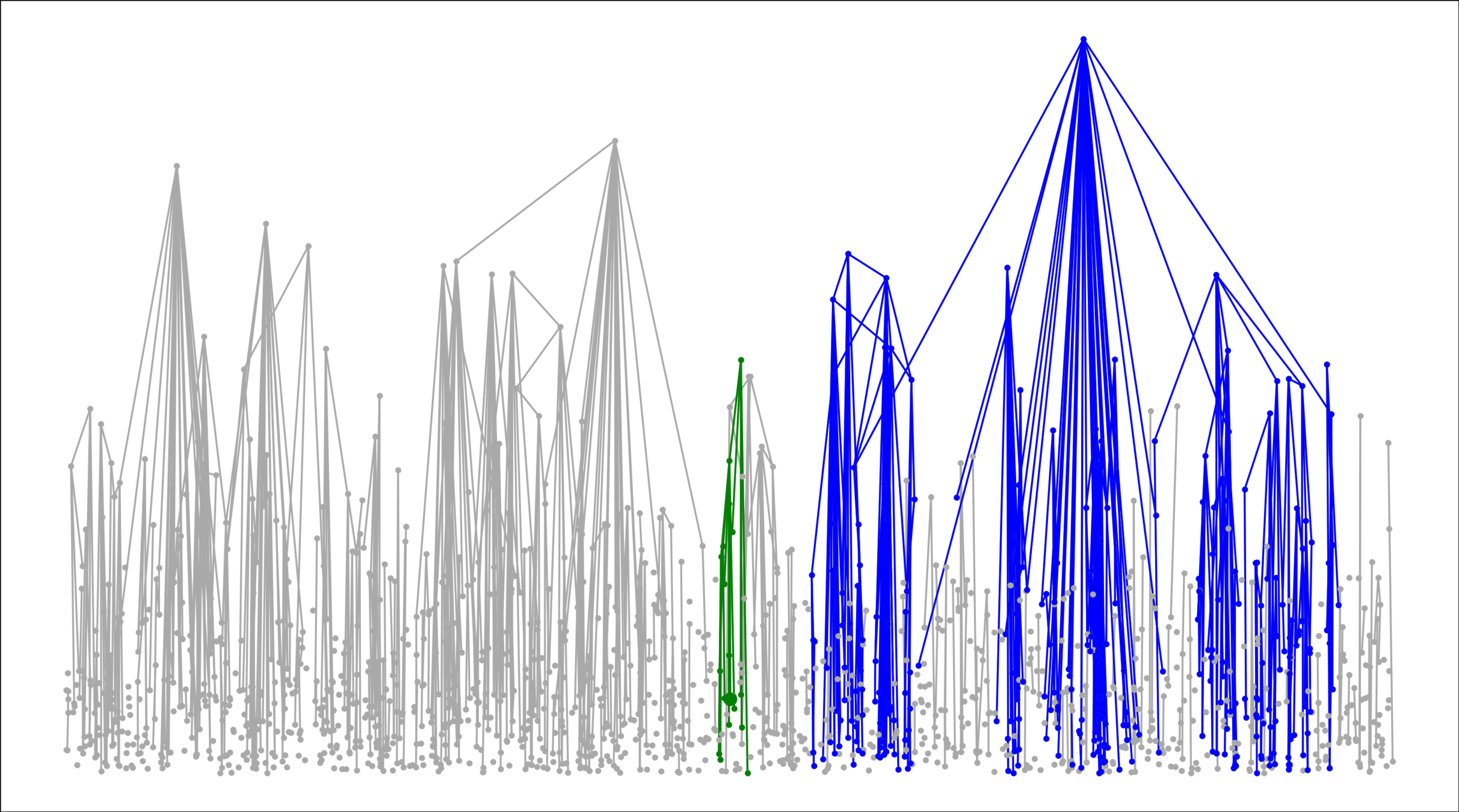
Age-dependent RCM

Theorem. When $\tau<2$ or $\alpha<1$:

Infinite degrees
Bounded diameter

[Deijfen, v.d. Hofstad, Hooghiemstra '13], [Gracar, Grauer, Lüchtrath, Mörters '18]

[Heydenreich, Hulshof, J. '17], [Hirsch '17], [v.d. Hofstad, v.d. Hoorn, Maitra '22],

[J., Komjáthy, Mitsche, '23], [Lüchtrath '22]

Theorem. When $\tau>2$ and $\alpha>1$:

$$\mathbb{P}(\mathrm{deg}(0)\ge k)\sim k^{-(\tau-1)}.$$

$\tau$ small: many hubs

$\alpha$ small: many long edges

Components in supercritical graphs

Largest component ${\color{blue}\mathcal{C}_n^{(1)}}$:
- Linear in box size
- Law of large numbers
- Lower tail large deviations
- Upper tail large deviations

Questions

Component of the origin ${\color{green}\mathcal{C}(0)}$: $$\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)= $$

Second-largest component: $$|{\color{red}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{what}\big)$$

Components in supercritical graphs

Largest component ${\color{blue}\mathcal{C}_n^{(1)}}$:
- Linear in box size
- Law of large numbers
- Lower tail large deviations
- Upper tail large deviations

Questions

Component of the origin ${\color{green}\mathcal{C}(0)}$: $$\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)= $$

Second-largest component: $$|{\color{red}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{what}\big)$$

Previous results

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\lesssim(\log n)^{??}

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}2/(3-\tau)}

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}d/(d-1)}

\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)

\sim \exp\!\big(\!\!-\!k^{\color{darkred}(d-1)/d}\big)

\lesssim \exp\big(\!-\!n^{\color{darkred} (d-1)/d}\big)

\lesssim \exp\big(\!-\!n^{\max(2-\alpha-o(1), (d-1)/d)}\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! \varepsilon n\big)

\lesssim \exp\big(\!-\!n^{\color{darkred}(3-\tau)/2}\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! \varepsilon n\big)

[Alexander & Chayes & Chayes '90], [Grimmett & Marstrand, '90], [Kesten & Zhang '90], ..., [Deuschel, Pisztora, '96], [Biskup '04], [Penrose '05], [Sly & Crawford'12], [Kiwi & Mitsche '17], [Lichev, Lodewijks, Mitsche, Schapira '22], [Bläsius, Friedrich, Ruff, Zeiff, '23]

Conjecture: $\exists \zeta\in \big[\tfrac{d-1}{d},1\big)$:

\sim \exp\big(\!-\!n^{\color{darkred}\zeta}\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! (1-\varepsilon ){\mathbb{E}\big[|{\color{blue}\mathcal{C}_n^{(1)}}|\big]}\big)

\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)

\sim \exp\big(\!-\!n^{\color{darkred}\zeta}\big)

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}1/\zeta}

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! \varepsilon n\big) \lesssim \exp\big(\!-\!n^{\color{darkred}\zeta}\big)

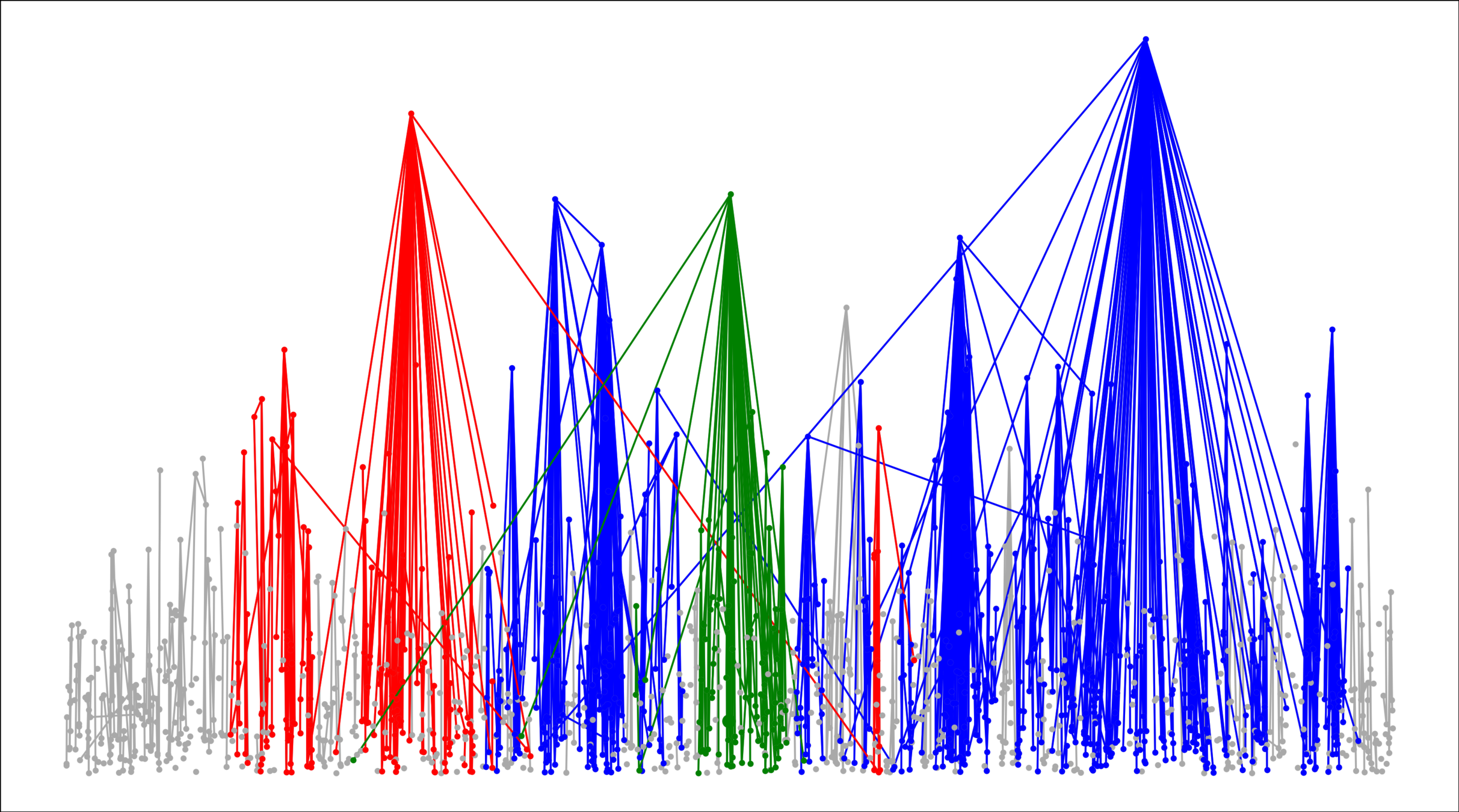
Remarks.

$\zeta_\ast<0$: subcritical*
$d\ge 2$:
- $(d-1)/d$
- partial results: upper bounds
Product kernel: 2nd term

No known results

$|{\color{blue}\text{largest}}|/n$
${\color{red}2^{\mathrm{nd}}\text{-largest}}$

Example 1:

Scale-free Gilbert RG in $d=1$

Power-law degrees: $\tau>2$

$d\ge 2$

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(3\!-\tau)/(2\!-\!(\tau\!-\!1)/\alpha) \}. \end{aligned}

* [Gracar, Lüchtrath, Mönch '22]

Theorem. (J., Komjáthy, Mitsche '23+)

Set

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(\tau\!-\!2)\!-\!(\tau\!-\!1)/\alpha \}. \end{aligned}

If $\zeta_\ast>0$, then LLN for $|{\color{blue}\text{largest}}|$, and

\mathbb{P}\big(|{\color{blue}\text{largest}}|\!\le\! (1-\varepsilon ){\mathbb{E}\big[|{\color{blue}\text{largest}}|\big]}\big)

\mathbb{P}\big(k\!\le\! |{\color{green}\mathcal{C}(0)}|\!<\!\infty\big)

\sim \exp\big(\!-\!n^{\color{darkred}\zeta_\ast}\big)

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\sim(\log n)^{\color{darkred}1/\zeta_\ast}

Long-range parameter: $\alpha>1$

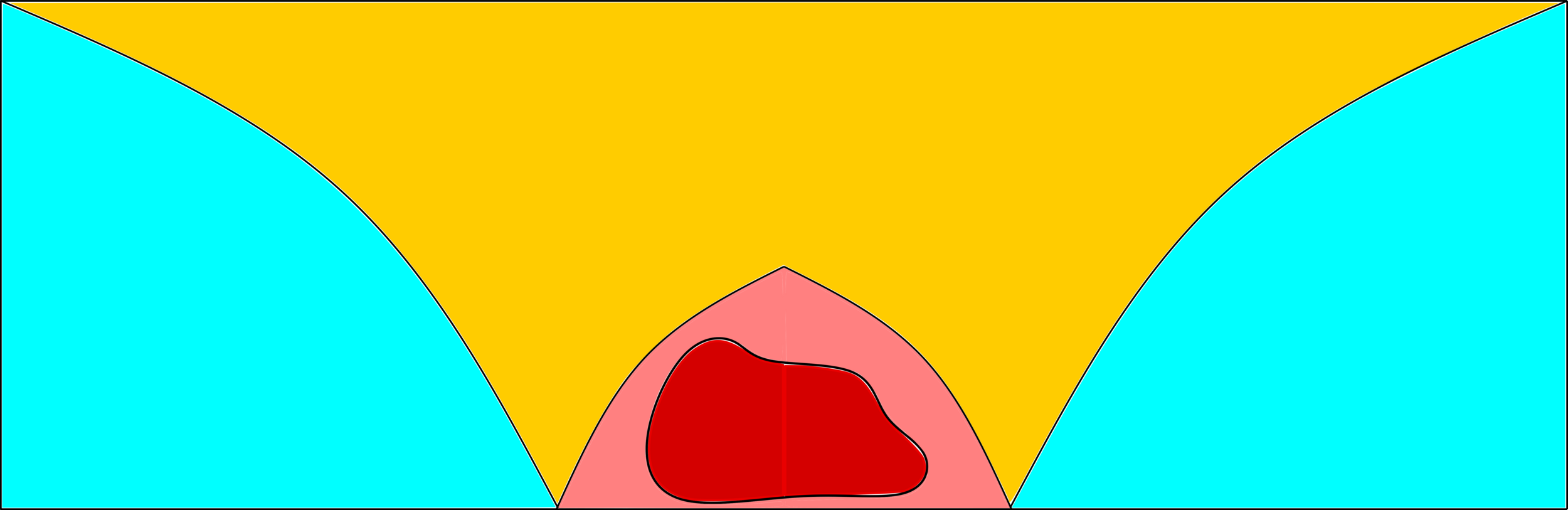
$\kappa_\mathrm{max}=w_u\vee w_v$

$\kappa_\mathrm{prod}=w_uw_v$

Example 2:

Geom. Inhomog. RG in $d=1$

{\color{green}\text{Cluster-size decay}}

|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

{\color{green}\text{Cluster-size decay}}

|{\color{red}2^{\mathrm{nd}}\text{-largest}}| \lesssim (\log n)^{1/\zeta}

{\color{blue}\text{LLN }}\text{to }\mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}

|{\color{blue}\text{largest}}| \text{ linear}

{\color{blue}\text{Lower tail large deviations}}

{\color{blue}\text{Lower tail of large deviations}}

Lower bounds: cluster-size decay

Aim: Find minimal $\zeta$ s.t.

\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\gtrsim\exp\big(-k^\zeta\big);

\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)

\sim\mathbb{P}\big(\mathcal{Q}_k\text{ isolated}\big)

\sim \exp\big(-k^\zeta\big)

|\mathcal{C}(0)|\ge k

\Bigg\}

\Theta(k)

\mathbb{E}[|\phantom{\square\square}|]\sim\mathbb{E}[|\phantom{\square\square}\leftrightarrow \phantom{\square\square}|]

Aim: Find $\gamma$ s.t.

\sim k^\zeta

Lower bounds: cluster-size decay

Aim: Find minimal $\zeta$ s.t.

\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\gtrsim\exp\big(-k^\zeta\big);

|\mathcal{C}(0)|\ge k

\Bigg\}

\Theta(k)

k^\zeta\sim\mathbb{E}\big[|\{v\in\Lambda_k: v\leftrightarrow \Lambda_k^c\}|\big]

\mathbb{E}[|\phantom{\square\square}|]\sim\mathbb{E}[|\phantom{\square\square}\leftrightarrow \phantom{\square\square}|]

Aim: Find $\gamma$ s.t.

\sim k^\zeta

Lower bounds: large deviations

\Bigg\}

\rho n/2

\mathbb{P}\big(|\mathcal{C}_n^{(1)}|\le \rho n\big)

\ge\,\mathbb{P}\big(\text{all }\frac{2}{\rho}\mathcal{Q}_{\tfrac{\rho n}2}\text{-boxes isolated, $\le\!\rho n$ vertices}\big)

\ge\,\Big(\mathbb{P}\big(\mathcal{Q}_{\tfrac{\rho n}2}\text{-box isolated, $\le\!\rho n$ vertices}\big)\Big)^{2/\rho}

\gtrsim\,\exp\big(-\tfrac{2}\rho(\tfrac{\rho n}2)^\zeta\big)

(FKG)

\Bigg\}

n^{1-\varepsilon}

\Bigg\}

(\delta' \log n)^{1/\zeta}

\mathbb{E}\big[\# \text{small isolated boxes}\big]

\gtrsim\, n^\varepsilon \exp\Big(-\big(\delta \log n)^{1/\zeta}\big)^\zeta\Big)

=\, n^{\varepsilon-\delta}

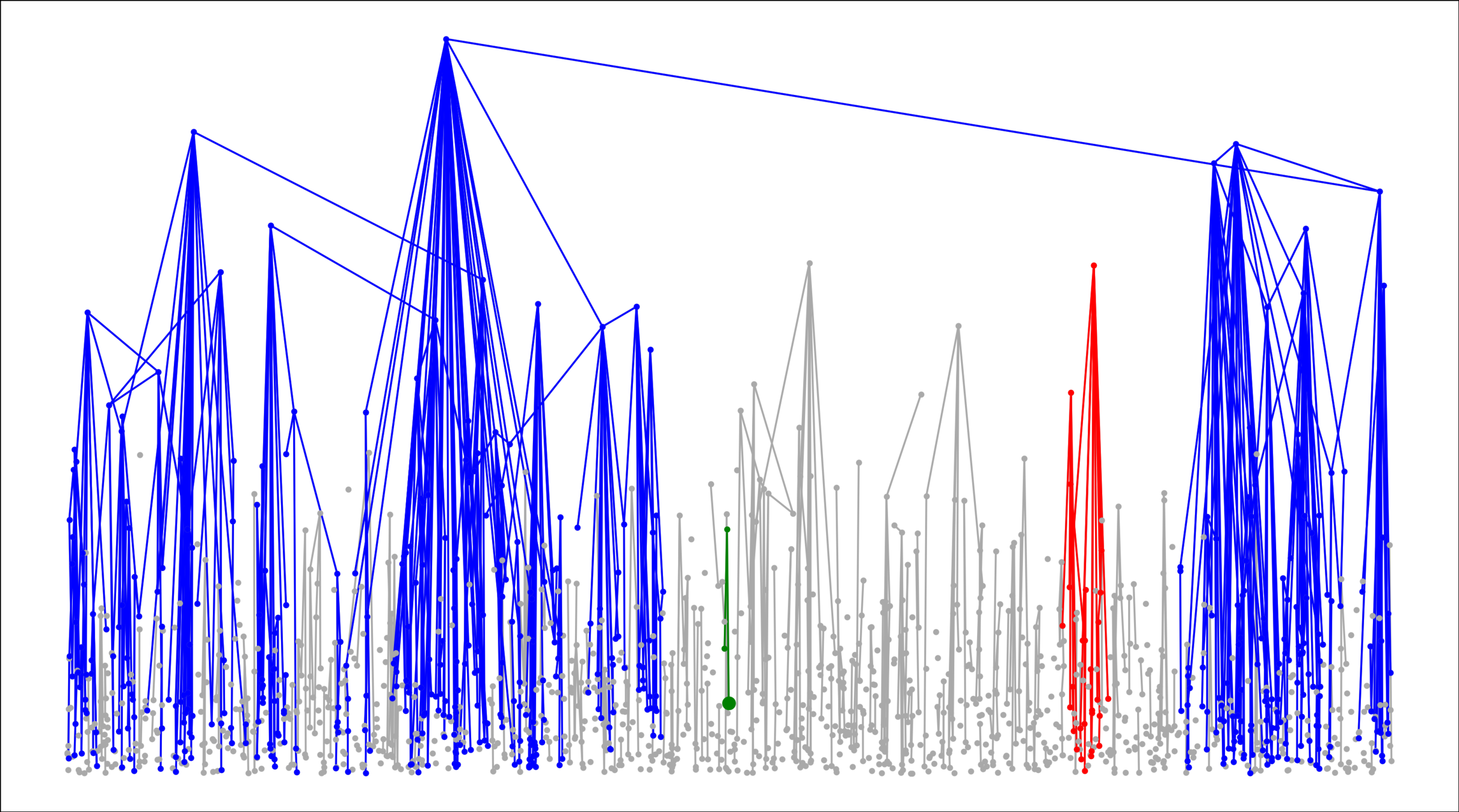
Lower bounds: $|\mathcal{C}_n^{(2)}|$

\mathbb{P}\big(|\mathcal{C}_n^{(2)}|\ge (\delta \log n)^{1/\zeta}\big)

\ge \, \mathbb{P}\big(\exists \text{isolated small box, no long edges}\big)

\longrightarrow\,\,\,\, \infty

$\delta$ small

{\color{green}\text{Cluster-size decay}}

Upper bounds

\mathbb{P}\big(|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

\text{Law of large numbers}

{\text{\color{blue}Lower tail large deviations}}

Challenge: Delocalized components

\binom{n}k \sim n^k \gg n\exp\big(k^\zeta\big)

# possibilities for $|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k$

Upper bound: $|\mathcal{C}_n^{(2)}|$

\mathbb{P}\big(|{\color{red}\mathcal{C}_n^{(2)}}|\ge k\big)\lesssim n\exp\big(-k^{2-\alpha}\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le \varepsilon \big)\lesssim \exp\big(-n^{2-\alpha}\big)

\mathbb{P}\big(\exists\text{ box without giant}\big)

\mathbb{P}\big(\exists\text{ neighboring giants not conn.}\big)

\lesssim (n/k)\exp\big(-k^{2-\alpha}\big)

\mathbb{P}\big(\nexists\text{ backbone}\big)

\lesssim (n/k)\exp\big(-k^{2-\alpha}\big)

\Bigg\}

\lesssim (n/k)(1-(2k)^{-\alpha})^{(\varepsilon k)^2}

\mathbb{P}\big(\text{size-}k\text{ component }\not\leftrightarrow\text{backbone}\big)

\lesssim\phantom{(n/k)}\exp\big(-k^{2-\alpha}\big)

\mathbb{P}\big(\exists \text{size-}k\text{ component }\not\leftrightarrow\text{backbone}\big)

\lesssim(n/k)\exp\big(-k^{2-\alpha}\big)

\mathbb{P}\big(|{\color{green}\mathcal{C}(0)}|\ge k, 0\notin{\color{blue}\text{largest}}\big)\lesssim \phantom{n}\exp\big(-k^\zeta\big)

Upper bounds

\mathbb{P}\big(|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

|{\color{blue}\text{largest}}|/n \overset{\mathbb{P}}\longrightarrow \vartheta:=\mathbb{P}\big(|{\color{green}\mathcal{C}(0)}|=\infty\big)

{\text{\color{blue}Lower tail large deviations}}

Truncation

Local convergence: giant is almost local

Lower tail of large deviations

|{\color{blue}\mathcal{C}_n^{(1)}}|/n \overset{\mathbb{P}}\longrightarrow \vartheta

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|\le \vartheta-\varepsilon\big)\lesssim \exp\big(-n^{2-\alpha}\big)

\Bigg\}

n^{\alpha-1}

$m_n\sim n^{2-\alpha}$ boxes

\mathbb{P}\big(|\mathcal{C}_{n^{\alpha-1}}^{(1)}|/n^{\alpha-1} \le \vartheta - \varepsilon\big)\le \varepsilon/2

\mathbb{P}\big(\text{more than }\varepsilon m_n\text{ non-giants}\big)\lesssim\exp\big(-n^{2-\alpha}\big)

\mathbb{P}\big(\text{giants connect}\big)\sim

n^{\alpha-1}n^{\alpha-1}n^{-\alpha}

\sim n^{-(2-\alpha)}

\ge \lambda/m_n

Lower tail of large deviations

|{\color{blue}\mathcal{C}_n^{(1)}}|/n \overset{\mathbb{P}}\longrightarrow \vartheta

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|\le \vartheta-\varepsilon\big)\lesssim \exp\big(-n^{2-\alpha}\big)

$m_n\sim n^{2-\alpha}$ boxes

\mathbb{P}\big(\text{giants connect}\big)\ge \lambda/m_n

\mathbb{P}\big(\text{ giant in }\text{ER}(m, \lambda/m)\text{ has size at least }\rho(\lambda)-\varepsilon\big)

\sim \exp\big(-m\big)

\mathbb{P}\big(\text{more than }\varepsilon m_n\text{ non-giants}\big)\lesssim\exp\big(-n^{2-\alpha}\big)

\Bigg\}

n/m_n

{\color{green}\text{Cluster-size decay}}

Upper bounds

\mathbb{P}\big(|{\color{red}2^{\mathrm{nd}}\text{-largest}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)

\mathbb{P}\big(|{\color{blue}\text{largest}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

\text{Law of large numbers}

{\text{\color{blue}Lower tail large deviations}}

What about other values $\zeta_\ast$?

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(3\!-\!\tau)\big/(2\!-\!(\tau\!-\!1)/\alpha) \}. \end{aligned}

\begin{aligned} \zeta_\ast := \max\{&2\!-\!\alpha,\\ &(\tau\!-\!1)/\alpha - (\tau-2)) \}. \end{aligned}

$\kappa_\mathrm{prod}=w_u w_v$

$\kappa_\mathrm{max}=w_u\vee w_v$

Description of weight distribution in large components

Prevent "small-to-large" merging

Components in supercritical graphs

Largest component ${\color{blue}\mathcal{C}_n^{(1)}}$:
- Linear in box size
- Law of large numbers
- Lower tail large deviations
- Upper tail large deviations

Answered questions ($d=1$)

Component of the origin ${\color{green}\mathcal{C}(0)}$: $$\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big)= $$

Second-largest component: $$|{\color{red}\mathcal{C}_n^{(2)}}|=\Theta\big(\phantom{what}\big)$$

Tales on tails: large deviations

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n<{\color{green}\vartheta}-\varepsilon\big)\sim \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n>{\color{green}\vartheta}+\varepsilon\big)\sim

n^{-(\tau-2)\lceil h(\varepsilon)\rceil}

h(\varepsilon):=\inf_{h'\ge1/2}\Big\{\mathbb{E}\Big[(1-p)^{h'|{\color{green}\mathcal{C}(0)}|}\Big]\le 1-({\color{green}\vartheta} + \varepsilon)\Big\}

Lower tail:

Upper tail:

# hubs ($w_v\sim n$) required: increase density from $\vartheta$ to $\vartheta+\varepsilon$

(Second-)largest component in supercritical spatial random graphs

Cluster-size decay

Second-largest component

Open problems:

Largest component:
- Linear in box size
- Law of large numbers
- Large deviations

Answered questions ($d=1$)

Phase transition boundaries.
Partial results $d\ge 2$
Extension from PPP to grid
Central limit theorem

$\zeta\in\big[(d-1)/d, 1\big)$

Thank you!

{\color{green}\text{Cluster-size decay}}

|{\color{red}\mathcal{C}_n^{(2)}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

{\color{green}\text{Cluster-size decay}}

|{\color{red}\mathcal{C}_n^{(2)}}| \lesssim (\log n)^{1/\zeta}

{\color{blue}\text{LLN }}\text{to }\mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}

|{\color{blue}\mathcal{C}_n^{(1)}}| \text{ linear}

{\color{blue}\text{Lower tail large deviations}}

{\color{blue}\text{Lower tail of large deviations}}

\alpha

\tau

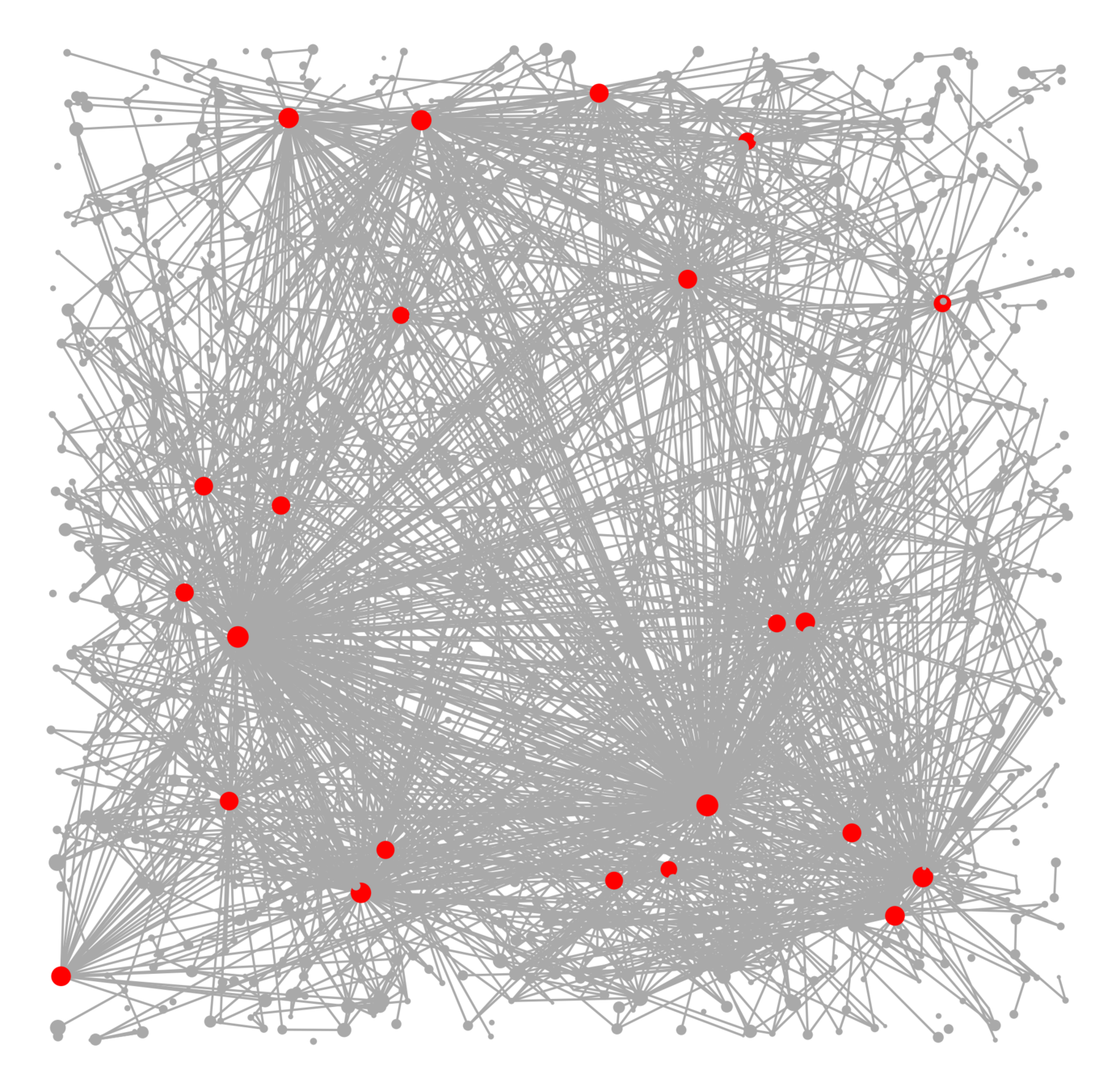
Small

Large

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \lesssim \phantom{n}\exp\big(-k^\zeta\big)

|{\color{red}\mathcal{C}_n^{(2)}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \gtrsim \exp\big(-k^\zeta\big)

\mathbb{P}\big(|{\color{red}\mathcal{C}_n^{(2)}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)

|{\color{blue}\mathcal{C}_n^{(1)}}|\! / n \overset{\mathbb{P}, L^1}\longrightarrow \mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta}-\varepsilon\big)\lesssim \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta} + \varepsilon\big]\big)\gtrsim \exp\big(-n^\zeta\big)

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \lesssim \phantom{n}\exp\big(-k^\zeta\big)

|{\color{red}\mathcal{C}_n^{(2)}}|\gtrsim (\log n)^{1/\zeta}

Lower bounds

Upper bounds

\mathbb{P}\big(k\le |{\color{green}\mathcal{C}(0)}|<\infty\big) \gtrsim \exp\big(-k^\zeta\big)

\mathbb{P}\big(|{\color{red}\mathcal{C}_n^{(2)}}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big)

|{\color{blue}\mathcal{C}_n^{(1)}}|\! / n \overset{\mathbb{P}, L^1}\longrightarrow \mathbb{P}(|{\color{green}\mathcal{C}(0)}|\!=\!\infty)=:{\color{green}\vartheta}

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le \varepsilon \big)\lesssim \phantom{n} \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta}-\varepsilon\big)\lesssim \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le {\color{green}\vartheta} - \varepsilon\big)\gtrsim \exp\big(-n^\zeta\big)

\mathbb{P}\big(|{\color{blue}\mathcal{C}_n^{(1)}}|/n\le 2\varepsilon \big)\longrightarrow 0

(Second-)largest component in spatial inhomogeneous random graphs

By joostjor

(Second-)largest component in spatial inhomogeneous random graphs