Spatial random graphs with tunable assortativity

Joost Jorritsma

joost.jorritsma@stats.ox.ac.uk

Intriguing maths: classical network models

Erdős–Rényi random graph \(G(n, \lambda /n)\)

Bernoulli percolation on \(\mathbb{Z}^2\) w.p. \(p\)

Intriguing maths: classical network models

Motivation 

  • Do there exist graphs with property X?


  • Is there a percolation phase transition?


  • What happens at the critical point?


  • What is the component-size distribution?

Intriguing maths: classical network models

Motivation 

  1. Universality: do all network (models) behave like ...?

     
  2. What are the implications for real-world networks?

Aim for this talk

  • Introduce model for type-1 question
     
  • Give modelling interpretation: degree assortativity
     
  • Is this model useful for applications?
    What should we investigate?

Universal properties demand null models

 

  1. Heavy-tailed degrees (power law: \(p_k\sim k^{-\tau}\))

     
  2. Small world: small distances compared to network size

     
  3. Clustering, local communities

     
  4. Geometry: (natural) embedding of nodes into space

     
  5. Hierarchy

Adapted from Network Science (2015), A.L. Barabási

Geometric inhomogeneous random graphs (GIRG)

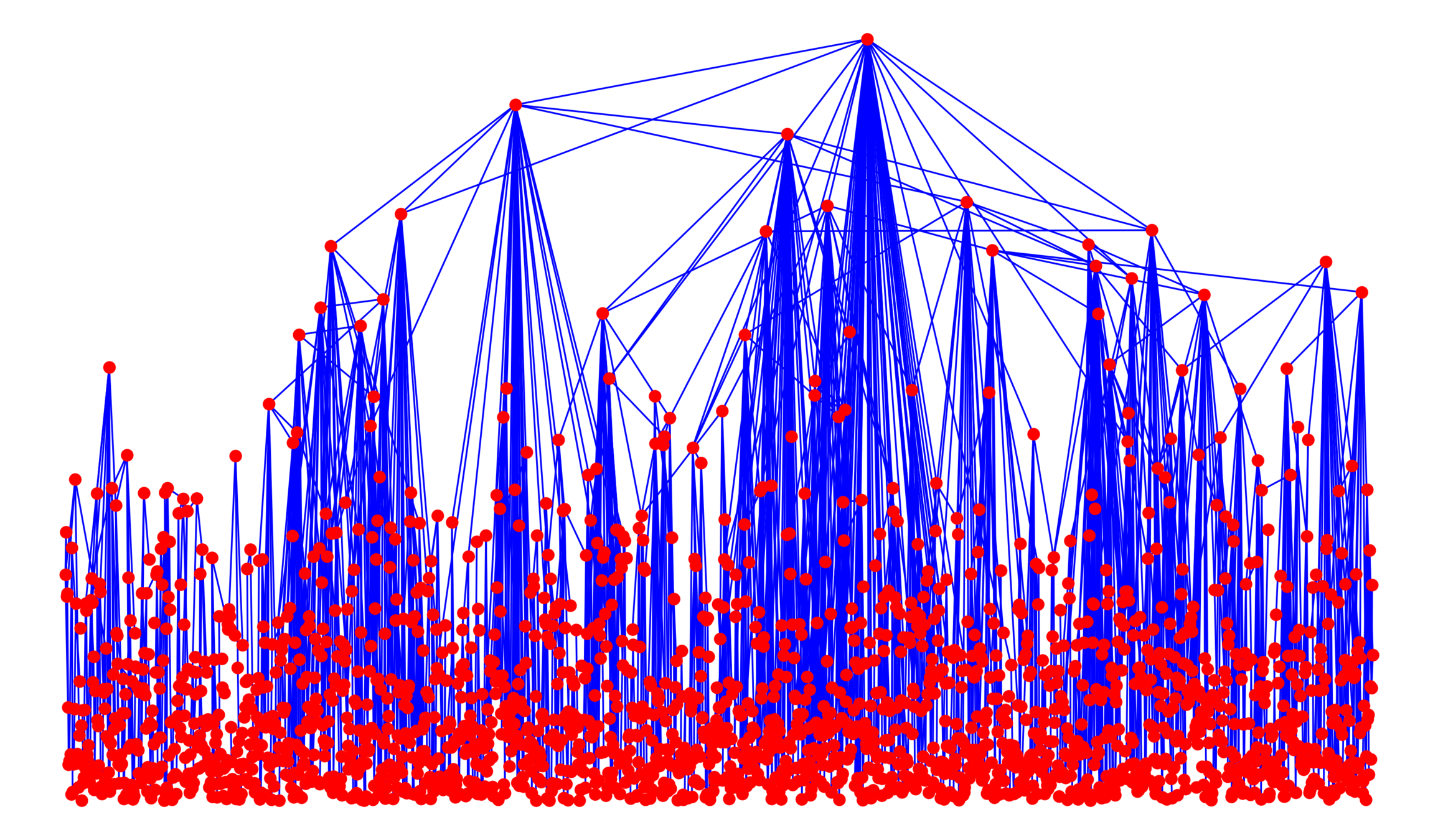
Vertex set \(\mathcal{V}_\infty\)

  • Spatial locations \(x_v\in\mathbb{R}^d\)
  • i.i.d. weights \(w_v\ge 1\): \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),

Edge set \(\mathcal{E}_\infty\)

  • High weight: high degree
  • Local clustering
  • Long-range parameter \(\alpha>1\),
  • Edge-density \(\beta>0\),

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{w_uw_v}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1$$

Vertex set \(\mathcal{V}_\infty\)

  • Spatial locations \(x_v\in\mathbb{R}^d\),
  • i.i.d. weights \(w_v\ge 1\): \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{w_uw_v}{\|x_u-x_v\|^d}\bigg)^\alpha$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{\bigg(\beta}\frac{w_uw_v}{\phantom{\|x_u-x_v\|^d}}\phantom{\bigg)^\alpha\wedge 1}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{\bigg(\beta}\frac{w_uw_v}{\|x_u-x_v\|^d}\phantom{\bigg)^\alpha\wedge 1}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\phantom{\beta}\frac{w_uw_v}{\|x_u-x_v\|^d}\bigg)^\alpha\phantom{\wedge 1}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)$$

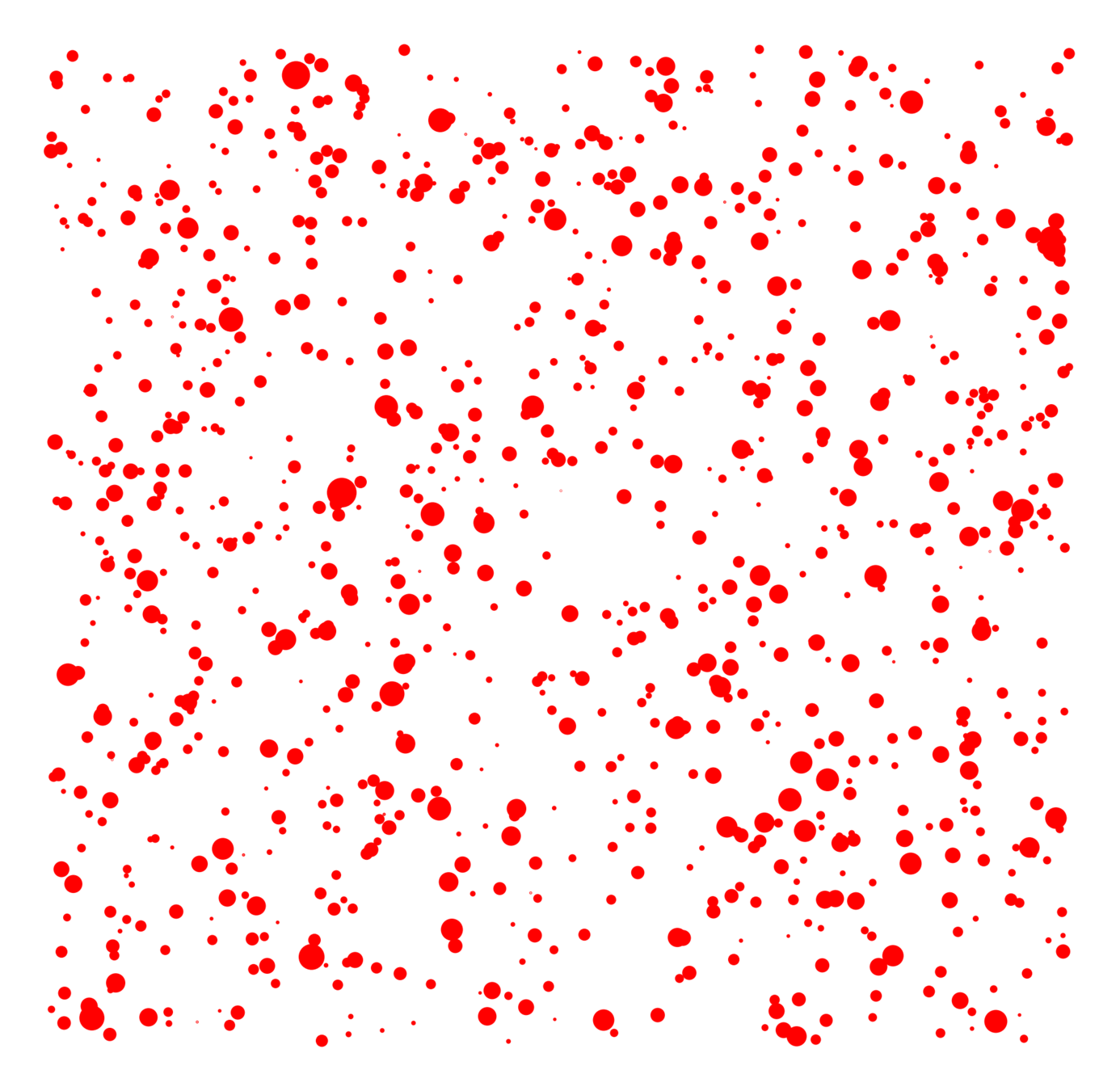
Geometric inhomogeneous random graphs (GIRG)

GIRG generalizes random hyperbolic graph (HRG)

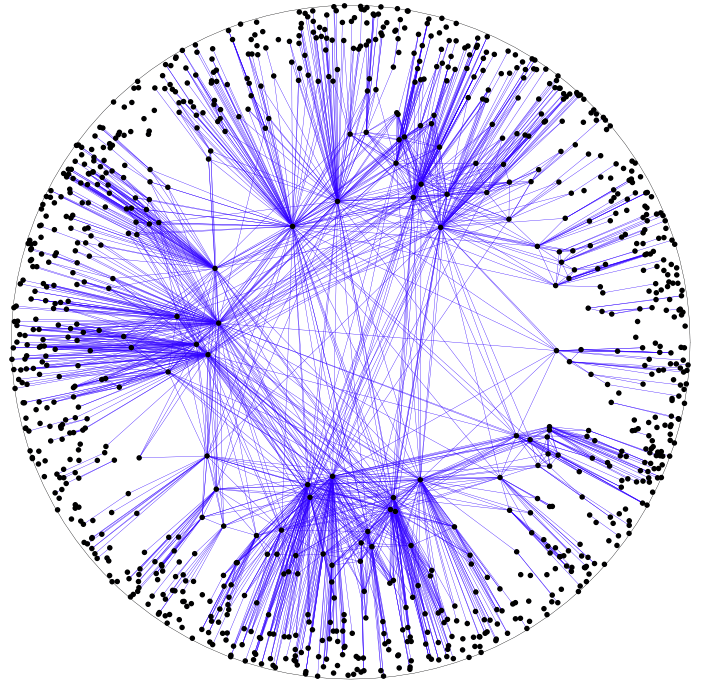
Figure by Tobias Müller

Hyperbolic random graph models Internet

Figure by Tobias Müller

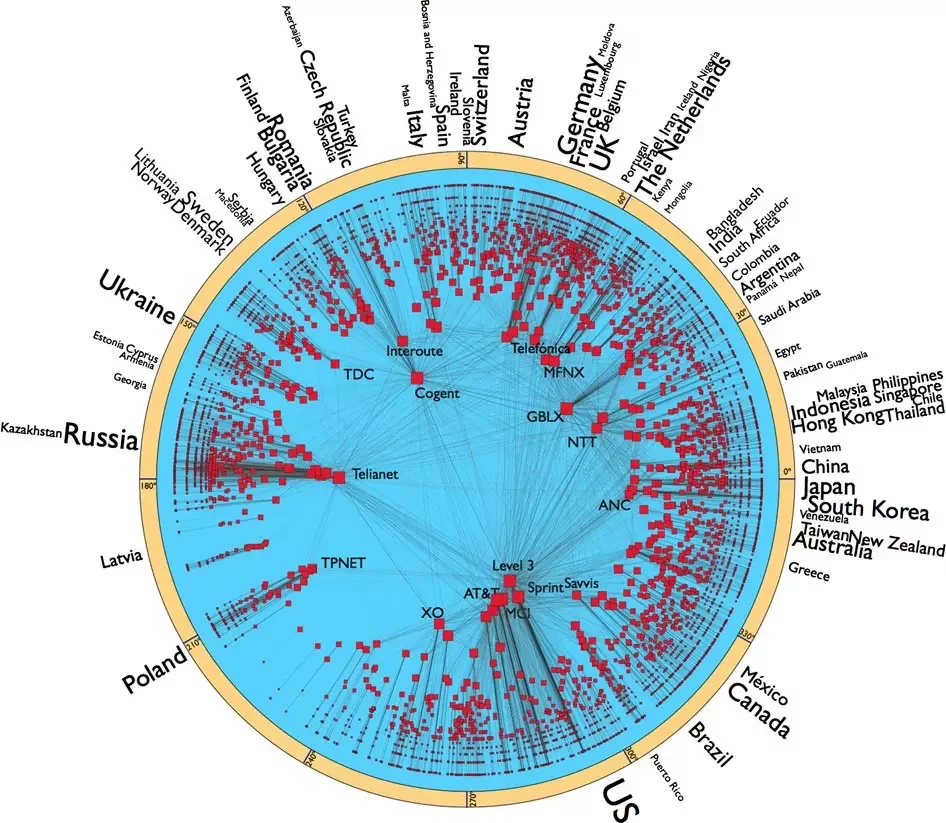
Boguñá, Papadopoulos & Krioukov (2010, Nature comm.)

GIRGs for understanding epidemics

[Odor, Czifra, Komjáthy, Lovasz, Karsai '21; Komjáthy, Lapinskas, Lengler '21]

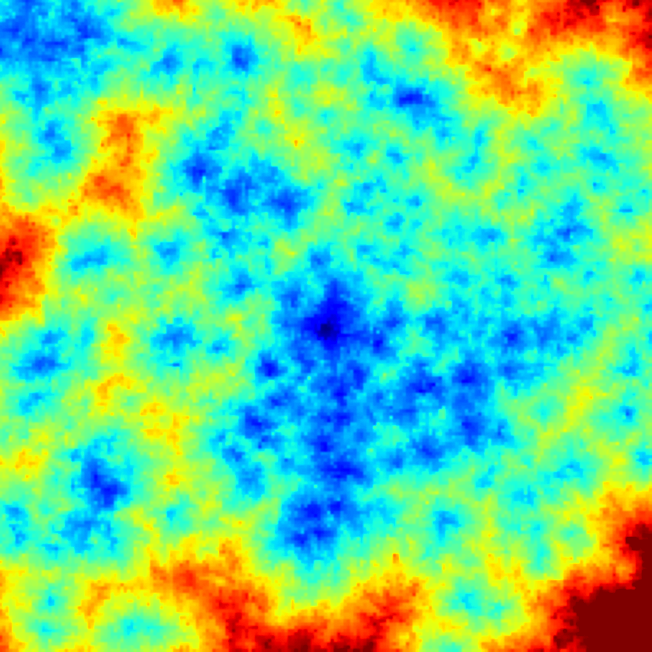
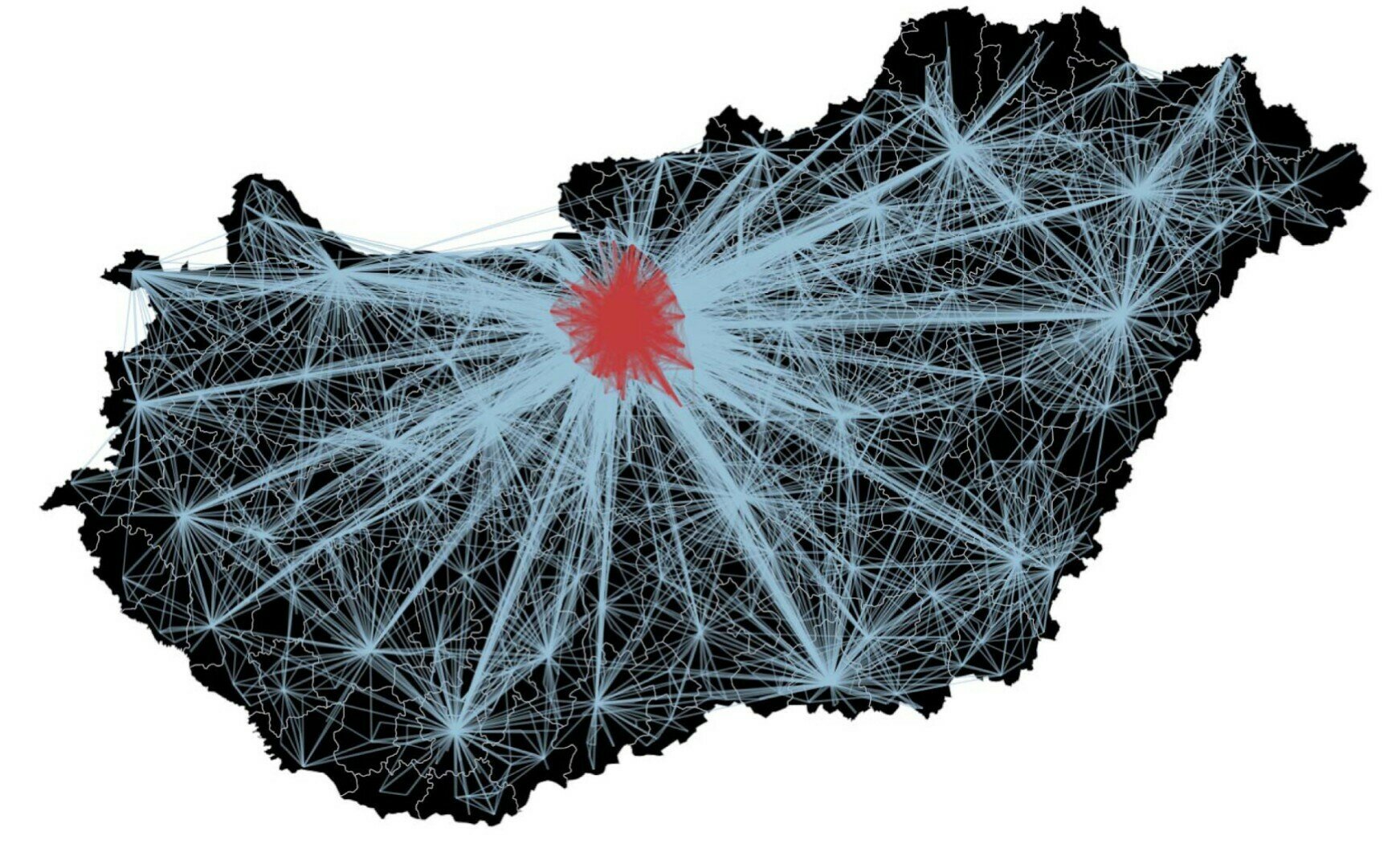
Back to math: epidemics via percolation

Vertex set \(\mathcal{V}_\infty\)

  • Spatial locations \(x_v\in\mathbb{R}^d\)  
  • i.i.d. weights : \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),

Edge set \(\mathcal{E}_\infty\)

 

  • Long-range parameter \(\alpha>1\),
  • Edge-density \(\beta>0\),
  • Percolation probability \(p\in[0,1]\)

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{p\bigg(}\bigg(\beta\frac{w_uw_v}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1\phantom{\bigg)}$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=p\bigg(\bigg(\beta\frac{w_uw_v}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1\bigg)$$

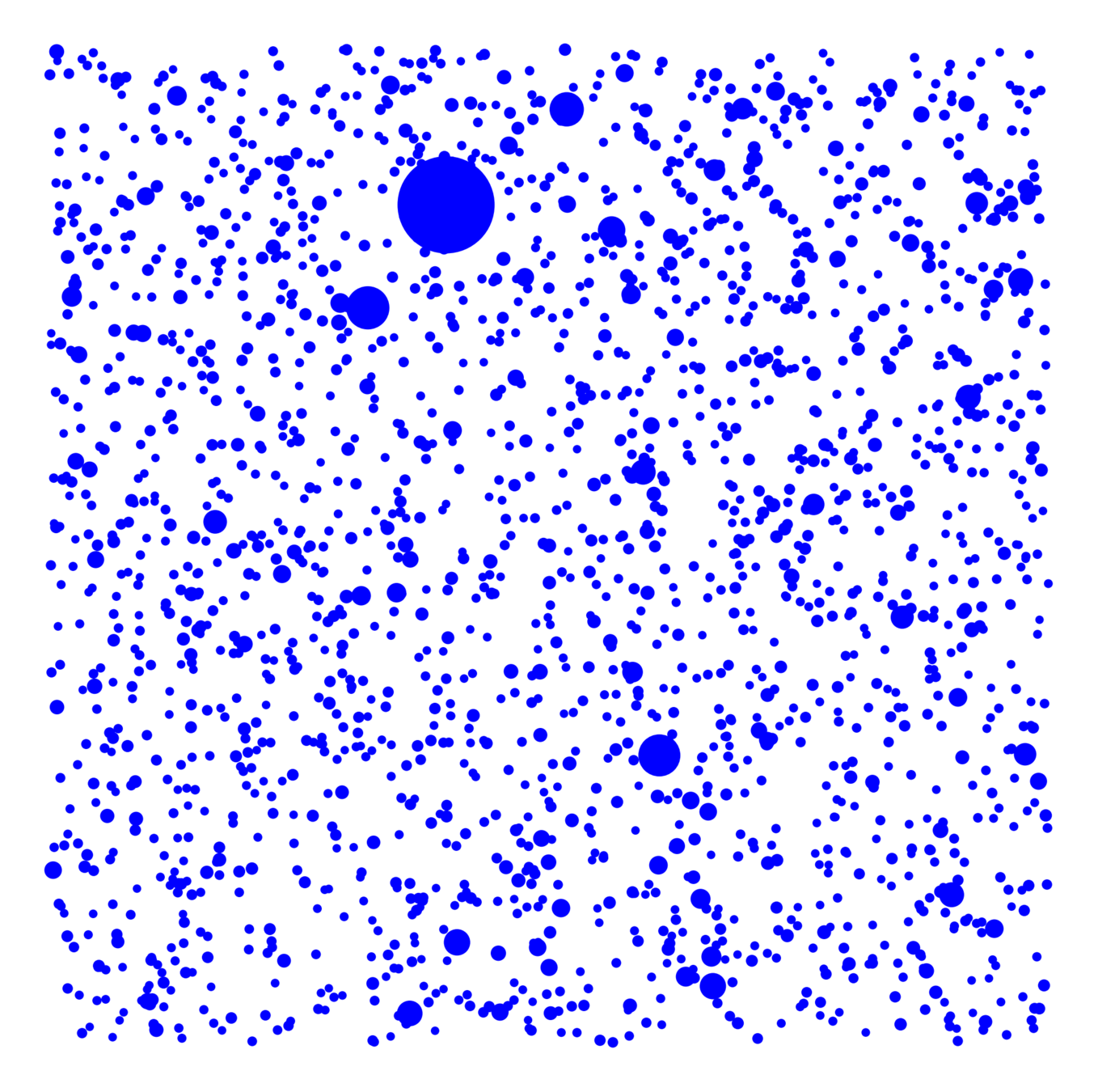
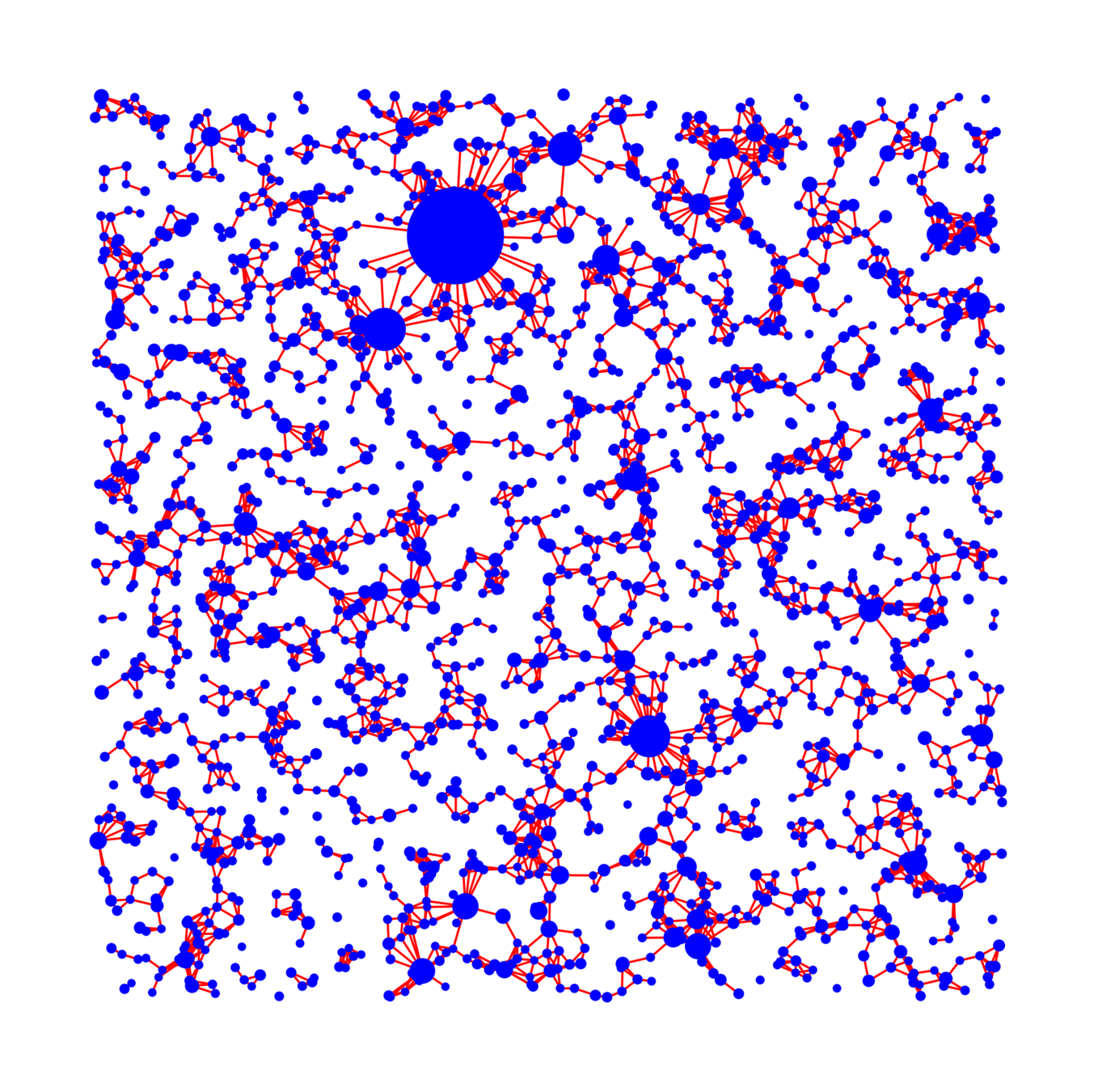
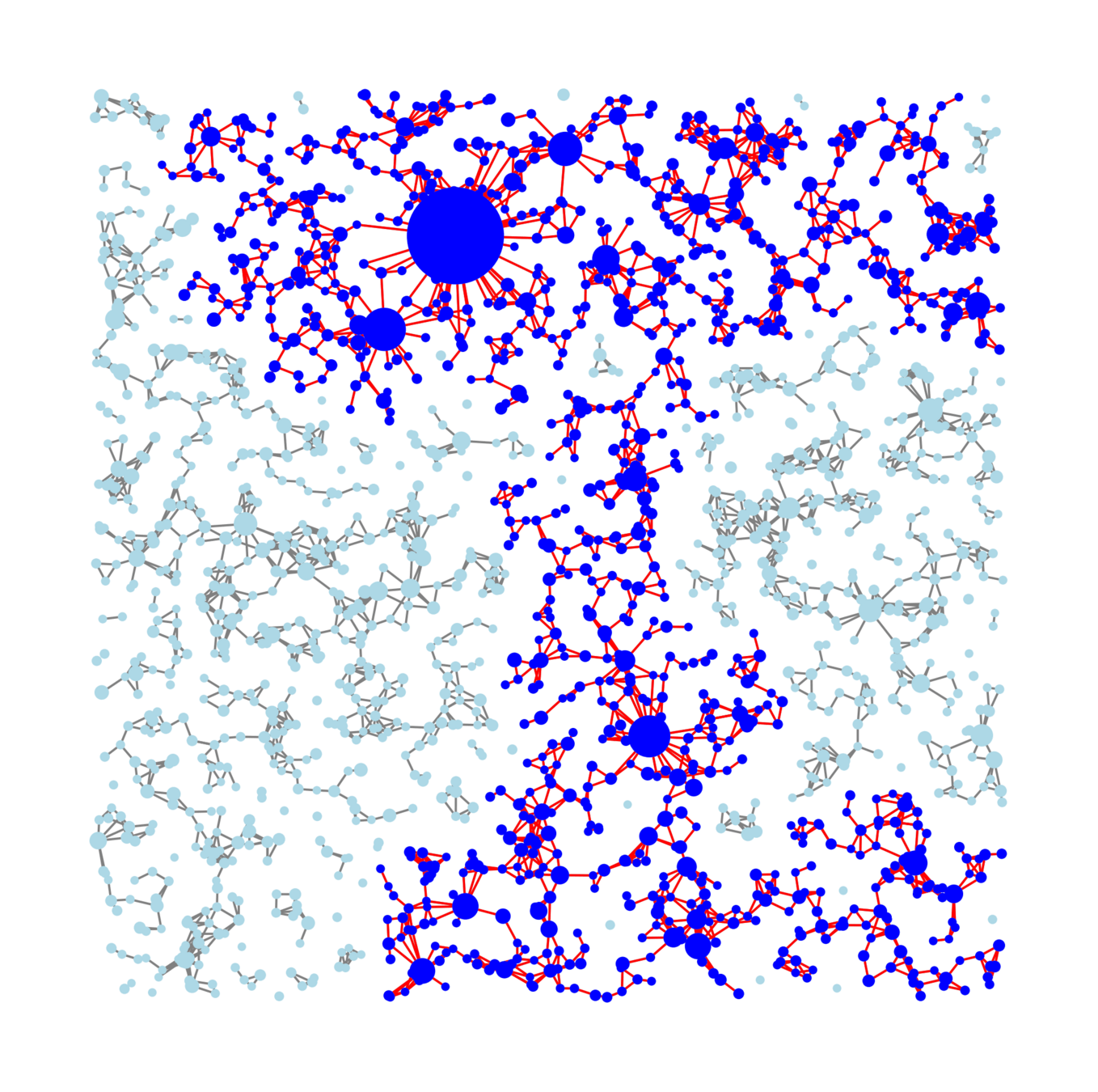
Question: Is there a non-trivial phase transition?

Bernoulli percolation on \(\mathbb{Z}^2\) w.p. \(p\)

Geometric inhomogeneous random graph

Q1: Is there a non-trivial phase transition?

GIRGs contain an infinite component when

  1. Weights have infinite variance (\(\tau\in(2,3)\)).

     
  2. Weights have finite variance, but
    enough short and long edges
    (\(\alpha\in(1,2), p, \beta\) large).

     
  3. Weights have finite variance, few long edges (\(\alpha>2\)), enough short edges, and dimension at least 2. 

 

Deijfen, vdHofstad, Hooghiemstra '13; Fountoulakis, Müller '18; Bringmann, Keusch, Lengler '19; Gracar, Lüchtrath, Mönch '25]

Q2: What do small components look like?

[J., Komjáthy, Mitsche '24, '24, '25]

Second-largest component, 

(Finite) Component of the origin

Asymptotic size-distribution, and shape
determined by variational problem  

Trade-off between 

  • long edges  - high weights
  • long edges  - low weights 
  • short edges - dimension
\zeta=\max\bigg(\frac{3-\tau}{2-(\tau-1)/\alpha}, \,2-\alpha, \,\frac{d-1}d\bigg)

Are these the only three possible shapes?

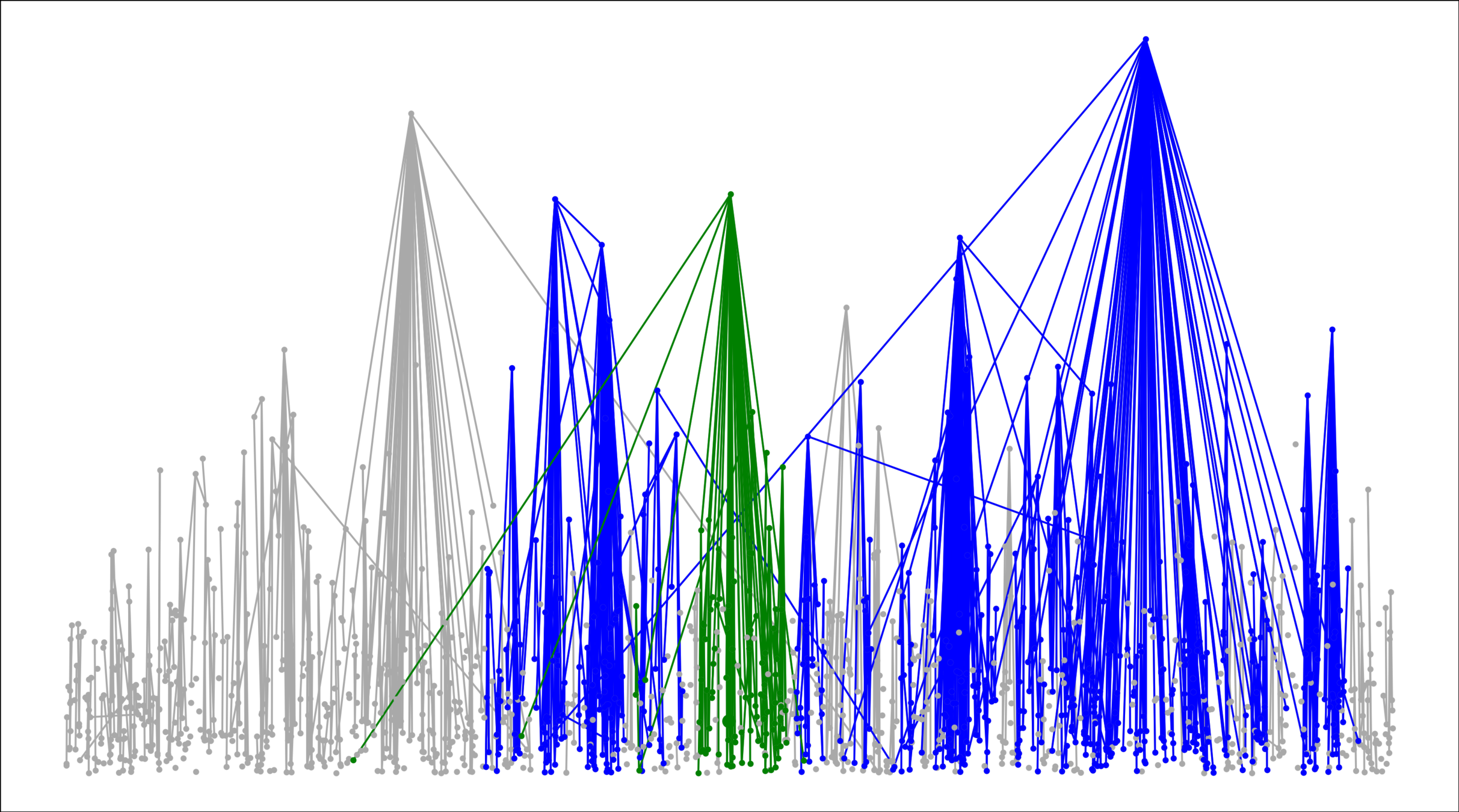
Hyperbolic random graph

GIRG

Long-range percolation

Spatial preferential attachment

Random geom. graph

Nearest-neighbor percolation

Kernel-based spatial random graphs (KSRG)

Connection probability

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{w_uw_v}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1$$

$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u,w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1$$

Kernel \(\kappa\):

Komjáthy, Lodewijks '18; Gracar, Heydenreich, Mönch, Mörters '19; Jorritsma, Komjáthy, Mitsche '24; Gracar, Lüchtrath, Mönch '25] 

The interpolating kernel generalizes many models

Connection probability

$${\color{grey}\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta}\frac{\kappa(w_u, w_v)}{\color{grey}\|x_u-x_v\|^d}{\color{grey}\bigg)^\alpha\wedge 1}$$

A parameterized kernel: \(\sigma\ge 0\)

$$\kappa_{\sigma}(w_u, w_v):=\max\{w_u, w_v\}\min\{w_u, w_v\}^\sigma$$

  • \(\tau: \mathbb{P}(w_v\ge w)=w^{-(\tau-1)}.\)
  • \(\sigma\): interpolation
\frac{\sigma}{\tau-1}
\frac1{\tau-1}
1
1
\sigma=\tau-1
\tau=2
\sigma=1
\sigma=1
\sigma=\tau-2
\sigma=\tau-2
\sigma=0
\sigma=0

GIRG

Hyperbolic RG

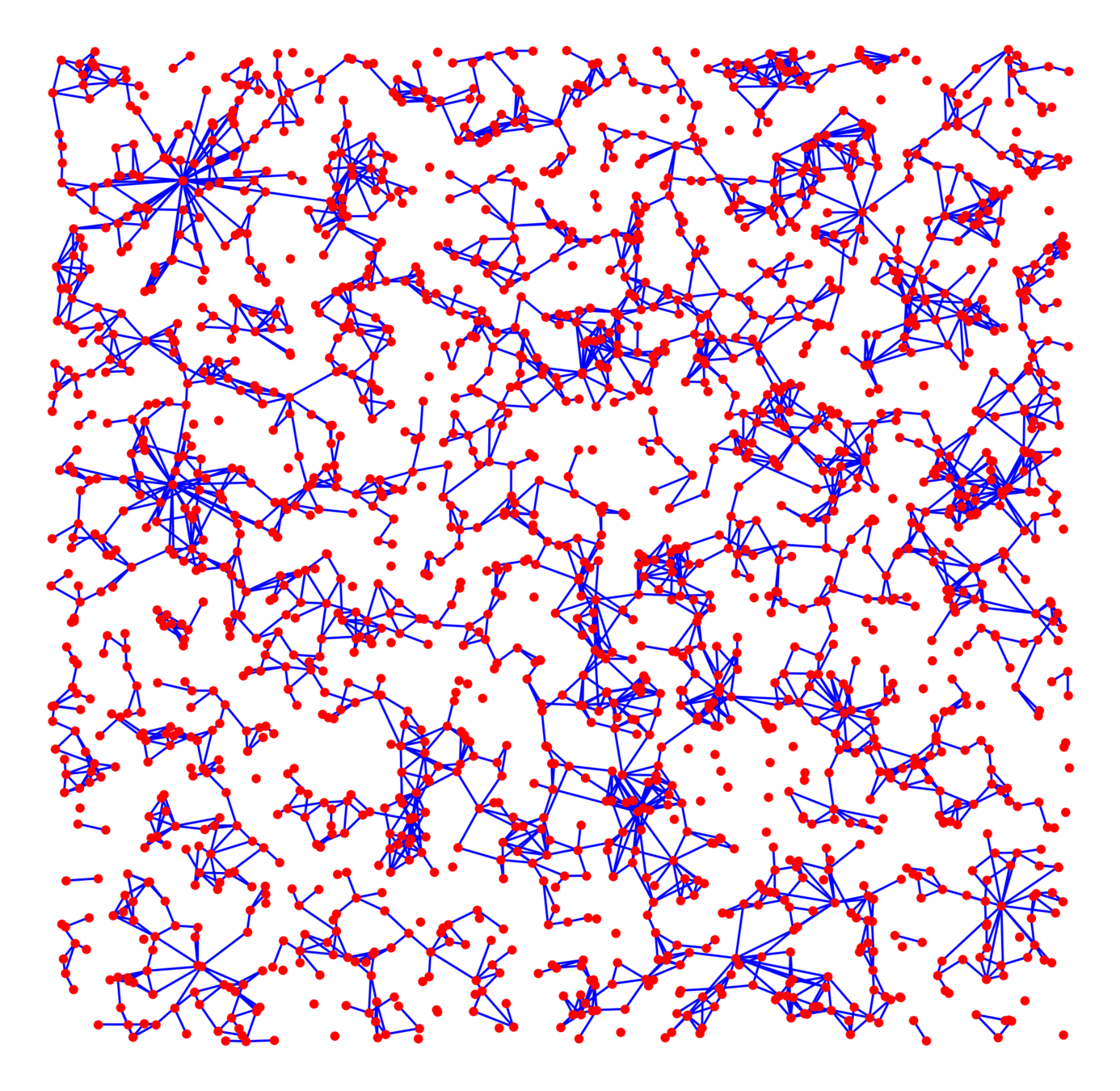
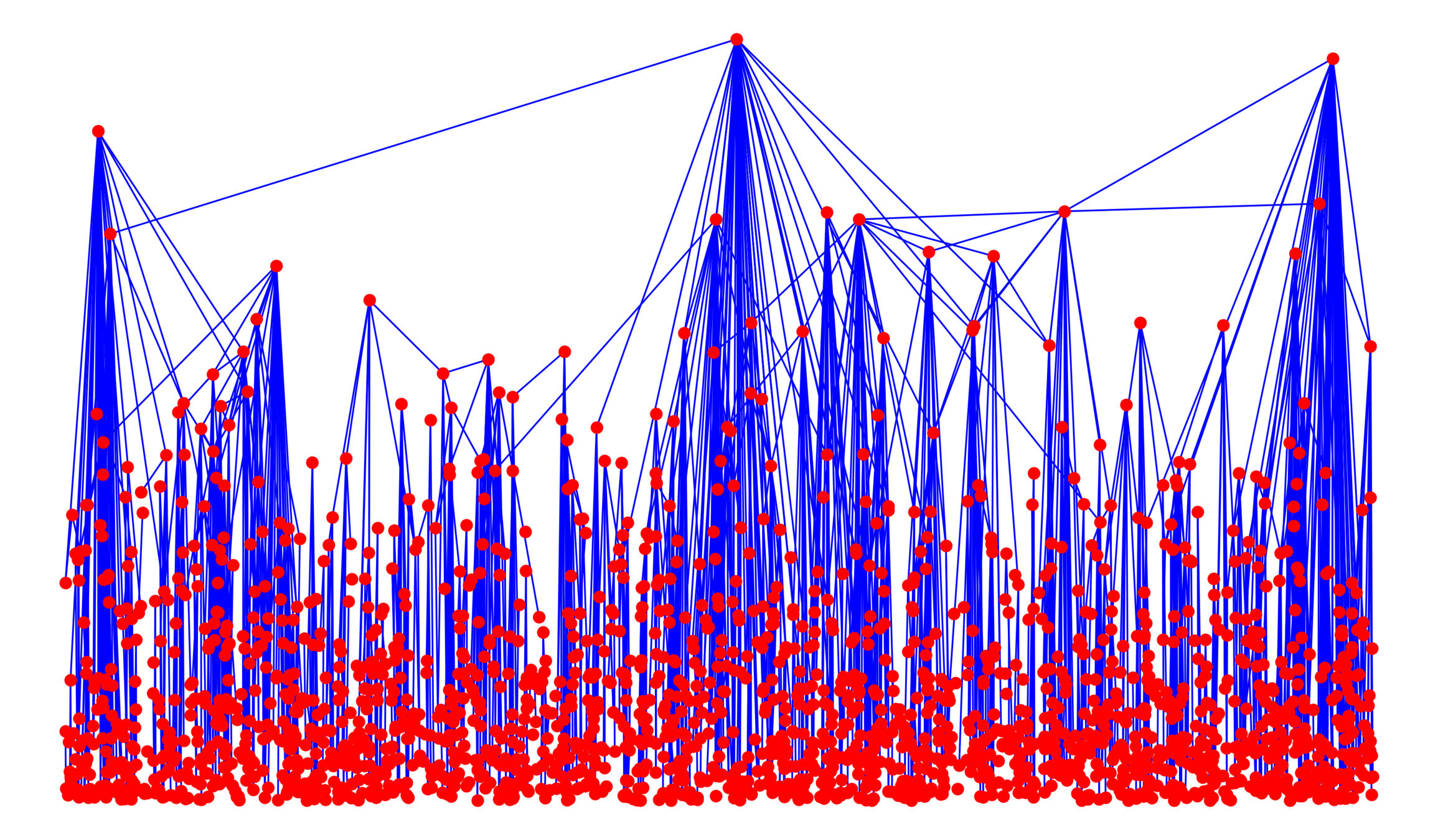
Spatial pref. attachment

Scale-free Gilbert

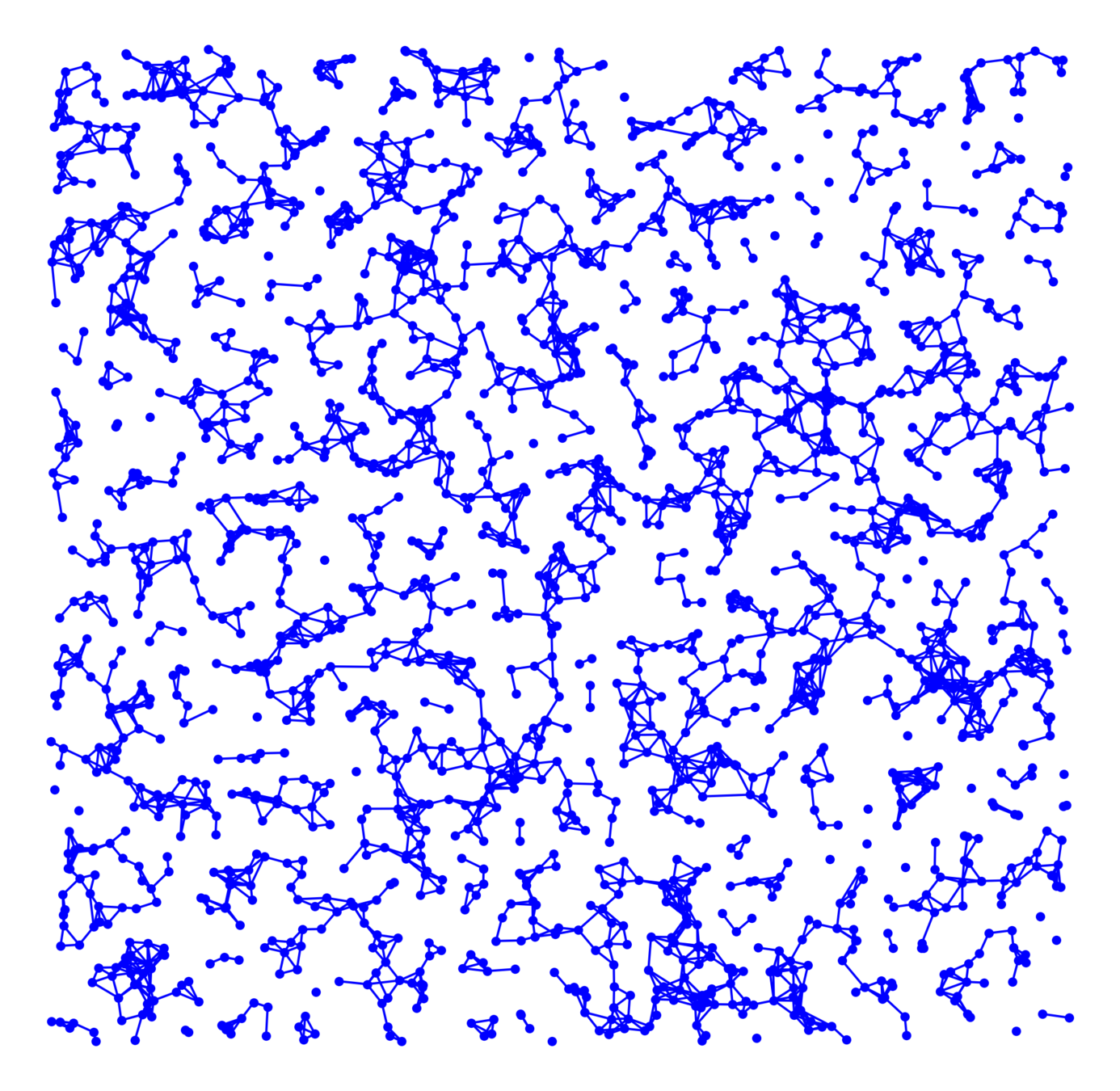
Long-range percolation

Random geom. graph

Nearest-neighbor percolation

Interpolation kernel tunes degree assortativity

Connection probability

$${\color{grey}\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta}\frac{\kappa(w_u, w_v)}{\color{grey}\|x_u-x_v\|^d}{\color{grey}\bigg)^\alpha\wedge 1}$$

A parameterized kernel, \(\sigma\in\mathbb{R}:\)

$$\kappa_{\sigma}(w_u, w_v):=\max\{w_u, w_v\}\min\{w_u, w_v\}^\sigma$$

Assortativity parameter

  • Weight-weight correlation of edges
  • Assortativity measures similarity between endpoints of an edge

Theorem. When \(\sigma<\tau-1\) : 

$$\big(\mathrm{deg}(v)\mid w_v=w\big) \sim \mathrm{Poi}(cw_v)$$

$$\mathbb{P}(w_v\ge w)=w^{-(\tau-1)},\quad \tau>2.$$

Interpolation kernel tunes degree assortativity

[Kaufmann, Schaller, Bläsius, Lengler '25+; Litvak, vdHofstad '13] 

Degree-degree correlation of edges

Correlation measures
(Pearson, Spearman, Kendall)
offer less/no insight

Plots based on 

$$\frac{\mathbb{P}(\mathrm{degree}(v)=y\mid \mathrm{degree}(u)=x)}{\mathbb{P}(\mathrm{degree}(v)=y)}$$

Interpolation kernel tunes degree assortativity

[Kaufmann, Schaller, Bläsius, Lengler '25+] 

Degree-degree correlation of edges

Tunable GIRGs offer rich model for networks

 

  1. Heavy-tailed degrees
     
  2. Small world: small distances compared to network size
     
  3. Clustering, local communities
     
  4. Geometry: (natural) embedding of nodes into space
     
  5. Hierarchy
     
  6. Flexible degree correlations

Time for questions!

 

joost.jorritsma@stats.ox.ac.uk

  • Are GIRGs with tunable assortativity useful?

     
  • What are theoretical properties to be studied?

     
  • Other questions?

Spatial random graphs with assortativity

By joostjor

Made with Slides.com

Spatial random graphs with assortativity

  • 22

More from joostjor

  • Copy of Largest component in spatial random graphs
    joostjor
    117
  • Copy of Largest component in spatial random graphs
    joostjor
    183
  • Copy of Largest component in spatial random graphs
    joostjor
    178