
\text{Image Processing (Fourier Domain)}
\textbf{Naresh Kumar Devulapally}
\text{CSE 4/573: Computer Vision and Image Processing}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}
\text{June 10, 2025}
\text{Lectures 5: June 10, 2025}
\text{Image Processing}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

- What is a Fourier Domain?
- How can images be converted to Fourier Domain?
- What are the advantages of Image Processing in Fourier Domain?
- Quantitative results of the gains in image processing.
\( \text{Agenda of this Lecture:}\)
\text{June 10, 2025}
\text{Time/Space Domain}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}
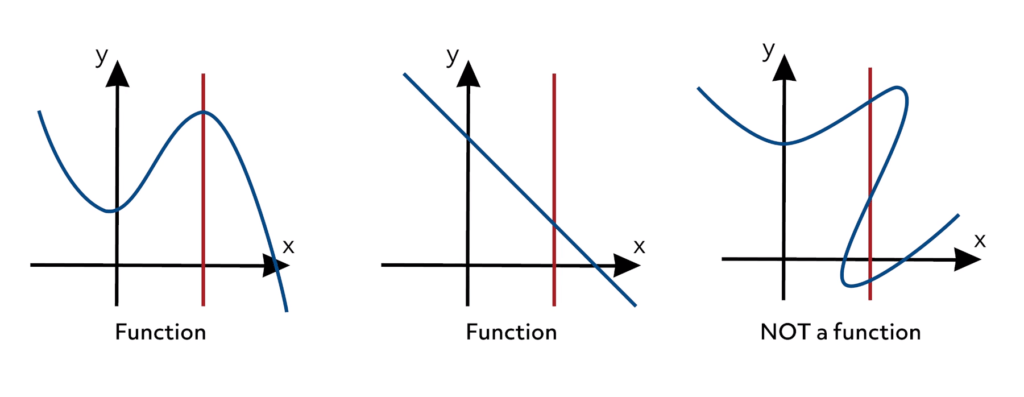
- A time-domain function describes how a quantity changes with time or space.
- Examples we see daily:
- Audio waveforms: \( f(t) \) = amplitude of sound at time \( t \).
- Temperature readings: \( T(x) \) = temperature at position \( x \).
Mathematically: \( f(t): \mathbb{R} \to \mathbb{R} \)
\text{Frequency (Fourier) Domain}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}
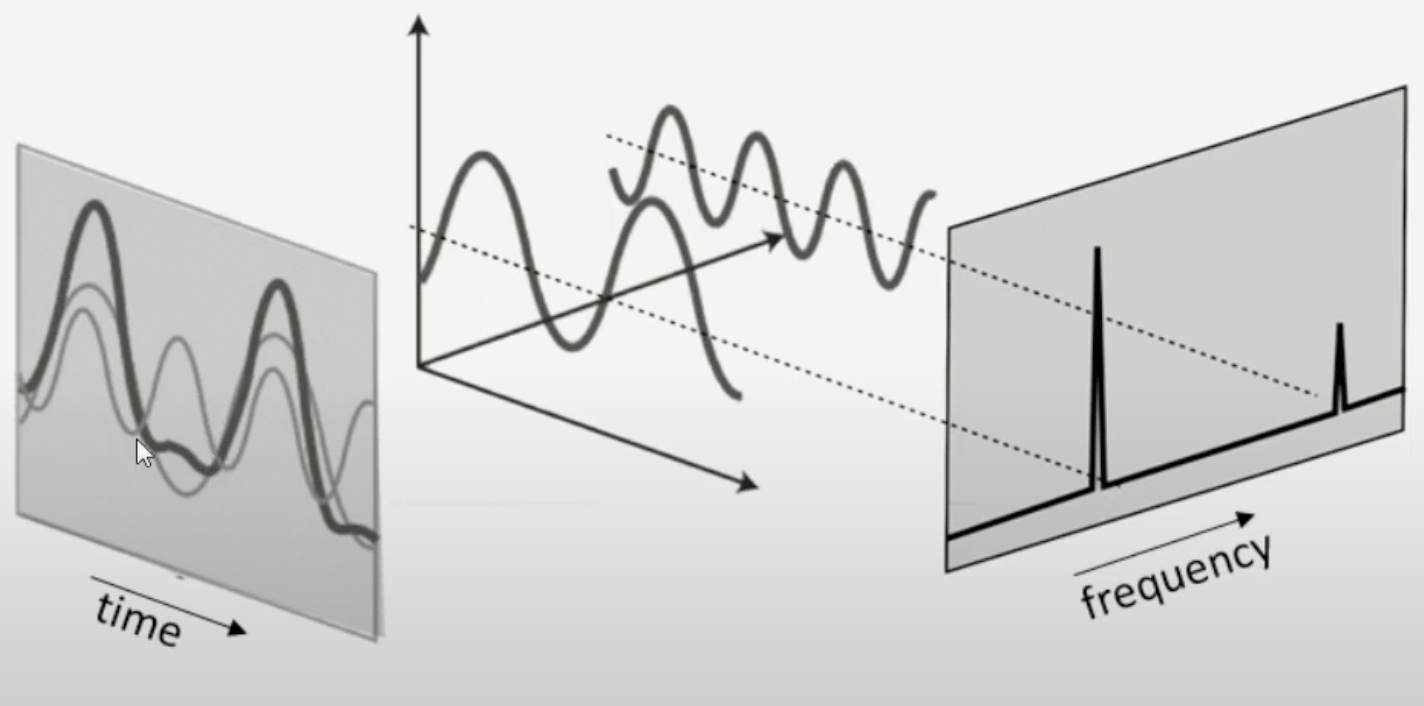
- The frequency domain expresses a signal as a sum of sinusoids.
- Instead of analyzing when things happen, we analyze what frequencies are present.
Example:
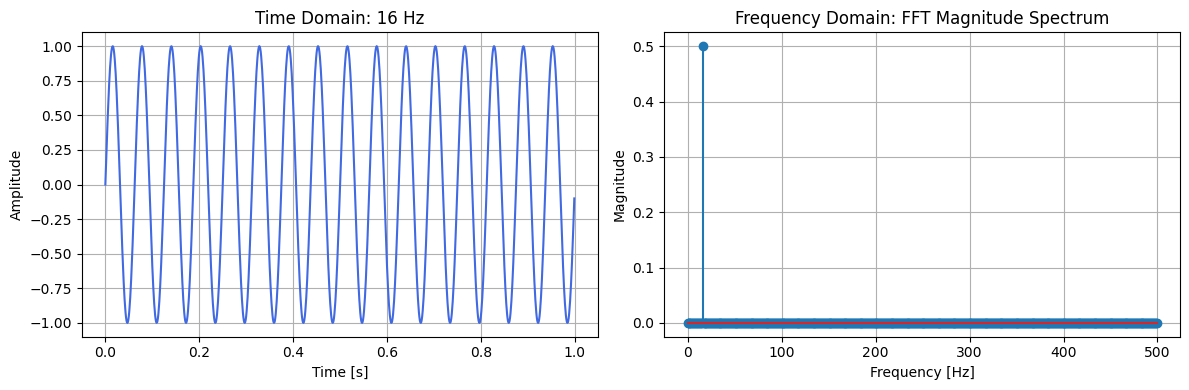
\( f(t) = \sin(2\pi \cdot 5t) \)
A 5 Hz sine wave has one spike at 5 Hz in frequency domain.
Fourier Transform:
\( F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i \omega t} \, dt\)
\text{Frequency (Fourier) Domain}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}
\text{Frequency (Fourier) Domain}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}
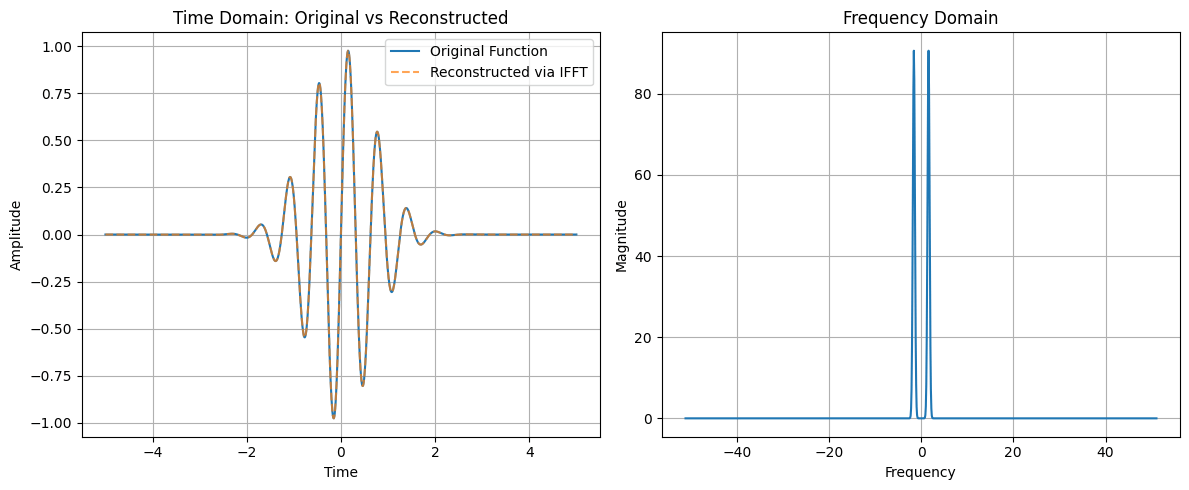
Head over to course website to interact with all these plots
\text{Interpretation of Image as a Function}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}
An image can be modeled as a 2D function:
\( I(x, y): \mathbb{R}^2 \to \mathbb{R} \)

\text{Fourier Transform of Images}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}

-
Center of FFT image: Low frequencies
- Smooth background, global patterns
-
Corners of FFT image: High frequencies
- Sharp transitions, edges, textures
\text{Fourier Transform of Images}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}
But Why Fourier Domain?
\text{Fourier Transform of Images}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}
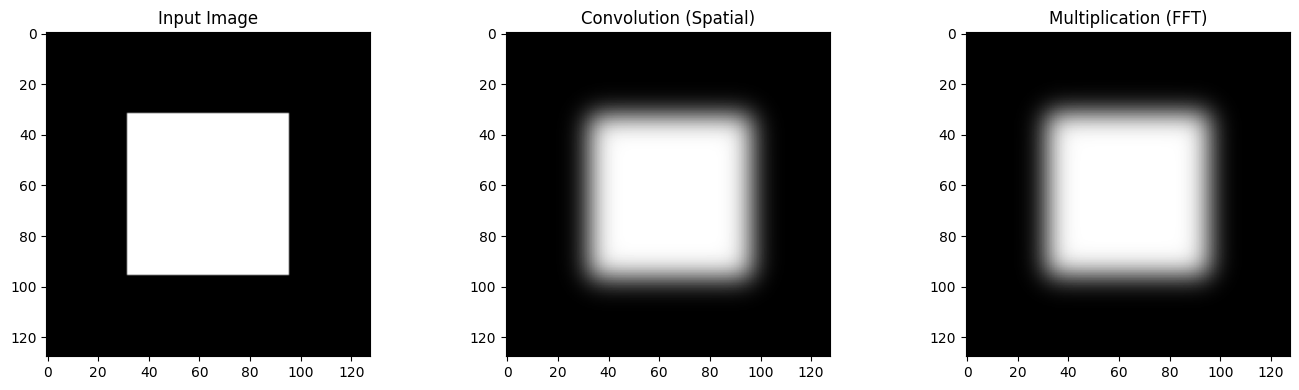

\text{Fourier Transform of Images}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}
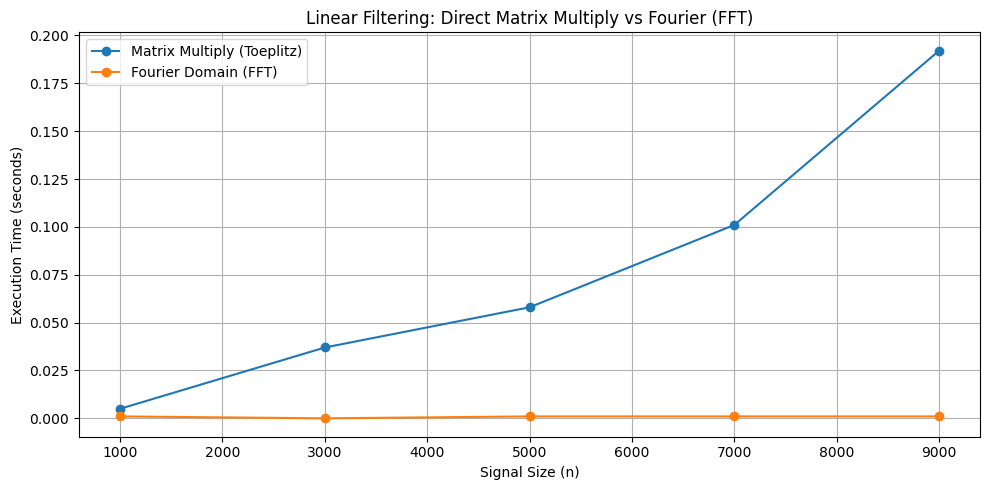
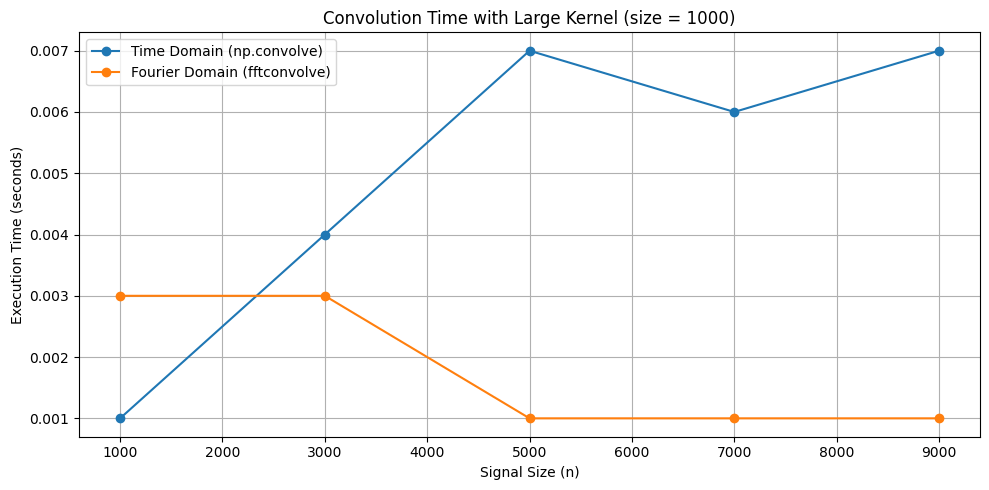
Any ongoing projects on this?
scipy.fftconvolve
FFC - Neurips 2020
\text{Fourier Transform of Images}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}

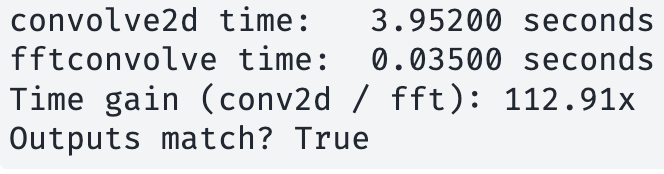
\text{Fourier Transform of Images}
\text{Naresh Kumar Devulapally}
\text{CSE 4/573: CVIP, Summer 2025}

\text{June 10, 2025}
That ends image processing in the Fourier Domain
Lecture 5: Image Processing (Fourier Domain)
By Naresh Kumar Devulapally
Lecture 5: Image Processing (Fourier Domain)
- 103



